初始化對訓練深度神經網絡的收斂性有重要影響。簡單的初始化方案可以加速訓練,但是它們需要小心避免常見的陷阱。
近期,deeplearning.ai就如何有效地初始化神經網絡參數發表了交互式文章,圖靈君將結合這篇文章與您一起探索以下問題:
1、有效初始化的重要性
2、梯度爆炸或消失的問題
3、什么是正確的初始化?
4、Xavier初始化的數學證明
一、有效初始化的重要性
要構建機器學習算法,通常需要定義一個體系結構(例如Logistic回歸,支持向量機,神經網絡)并訓練它來學習參數。 以下是神經網絡的常見訓練過程:
1、初始化參數
2、選擇優化算法
3、重復這些步驟:
a、正向傳播輸入
b、計算成本函數
c、使用反向傳播計算與參數相關的成本梯度
d、根據優化算法,使用梯度更新每個參數
然后,給定一個新的數據點,您可以使用該模型來預測它的類。
初始化步驟對于模型的最終性能至關重要,它需要正確的方法。 為了說明這一點,請考慮下面的三層神經網絡。 您可以嘗試使用不同的方法初始化此網絡,并觀察它對學習的影響。
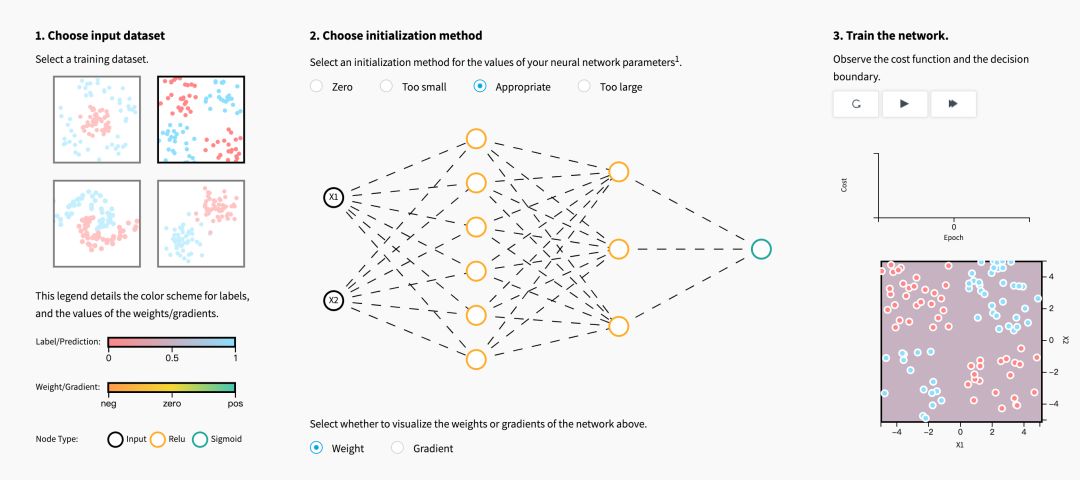
當初始化方法為零時,對于梯度和權重,您注意到了什么?
用零初始化所有權重會導致神經元在訓練期間學習相同的特征。
實際上,任何常量初始化方案的性能表現都非常糟糕。 考慮一個具有兩個隱藏單元的神經網絡,并假設我們將所有偏差初始化為0,并將權重初始化為一些常數α。 如果我們在該網絡中正向傳播輸入(x1,x2),則兩個隱藏單元的輸出將為relu(αx1+αx2)。 因此,兩個隱藏單元將對成本具有相同的影響,這將導致相同的梯度。
因此,兩個神經元將在整個訓練過程中對稱地進化,有效地阻止了不同的神經元學習不同的東西。
在初始化權重時,如果值太小或太大,關于成本圖,您注意到了什么?
盡管打破了對稱性,但是用值(i)太小或(ii)太大來初始化權重分別導致(i)學習緩慢或(ii)發散。
為高效訓練選擇適當的初始化值是必要的。我們將在下一節進一步研究。
二、梯度的爆炸或消失問題
考慮這個9層神經網絡。

在優化循環的每次迭代(前向,成本,后向,更新)中,我們觀察到當您從輸出層向輸入層移動時,反向傳播的梯度要么被放大,要么被最小化。 如果您考慮以下示例,此結果是有意義的。
假設所有激活函數都是線性的(標識函數)。 然后輸出激活是:
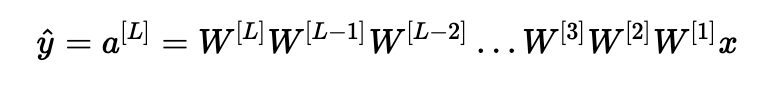
其中,L=10,W[1],W[2],…,W[L?1]都是大小為(2,2)的矩陣,因為層[1]到[L-1]有2個神經元,接收2個輸入。考慮到這一點,為了便于說明,如果我們假設W[1]=W[2]=?=W[L?1]=W,輸出預測是y^=W[L]WL?1x(其中WL?1將矩陣W取為L-1的冪,而W[L]表示Lth矩陣)。
初始化值太小,太大或不合適的結果是什么?
情形1:過大的初始化值會導致梯度爆炸
考慮這樣一種情況:初始化的每個權重值都略大于單位矩陣。
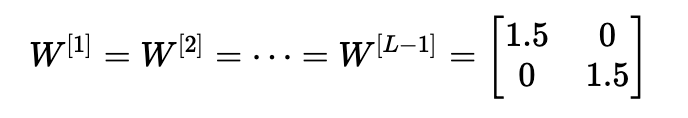
這簡化為y^=W[L]1.5L?1x,并且a[l]的值隨l呈指數增加。 當這些激活用于反向傳播時,就會導致梯度爆炸問題。 也就是說,與參數相關的成本梯度太大。 這導致成本圍繞其最小值振蕩。
情形2:初始化值太小會導致梯度消失
類似地,考慮這樣一種情況:初始化的每個權重值都略小于單位矩陣。
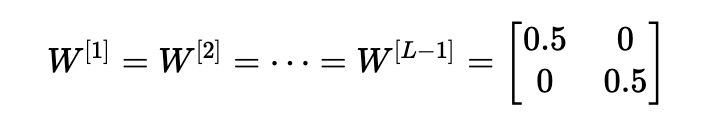
這簡化為y^=W[L]0.5L?1x,并且激活a [l]的值隨l呈指數下降。 當這些激活用于反向傳播時,這會導致消失的梯度問題。 相對于參數的成本梯度太小,導致在成本達到最小值之前收斂。
總而言之,使用不適當的值初始化權重將導致神經網絡訓練的發散或減慢。雖然我們用簡單的對稱權重矩陣說明了梯度爆炸/消失問題,但觀察結果可以推廣到任何太小或太大的初始化值。
三、如何找到合適的初始化值
為了防止網絡激活的梯度消失或爆炸,我們將堅持以下經驗法則:
1、激活的平均值應為零。
2、激活的方差應該在每一層保持不變。
在這兩個假設下,反向傳播的梯度信號不應該在任何層中乘以太小或太大的值。 它應該移動到輸入層而不會爆炸或消失。
更具體地考慮層l, 它的前向傳播是:
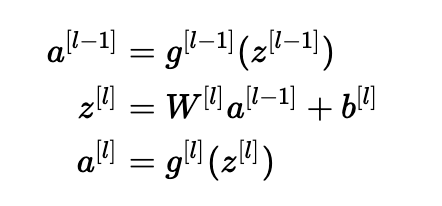
我們希望以下內容:
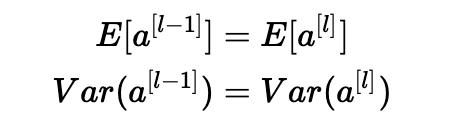
確保零均值并保持每層輸入方差的值不會產生爆炸/消失信號,我們稍后會解釋。 該方法既適用于前向傳播(用于激活),也適用于反向傳播傳播(用于激活成本的梯度)。 推薦的初始化是Xavier初始化(或其派生方法之一),對于每個層l:
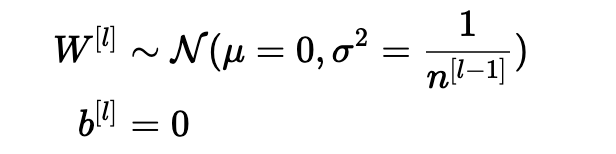
換句話說,層l的所有權重是從正態分布中隨機選取的,其中均值μ= 0且方差σ2= n [l-1] 1其中n [l-1]是層l-1中的神經元數。 偏差用零初始化。
下面的可視化說明了Xavier初始化對五層全連接神經網絡的每個層激活的影響。
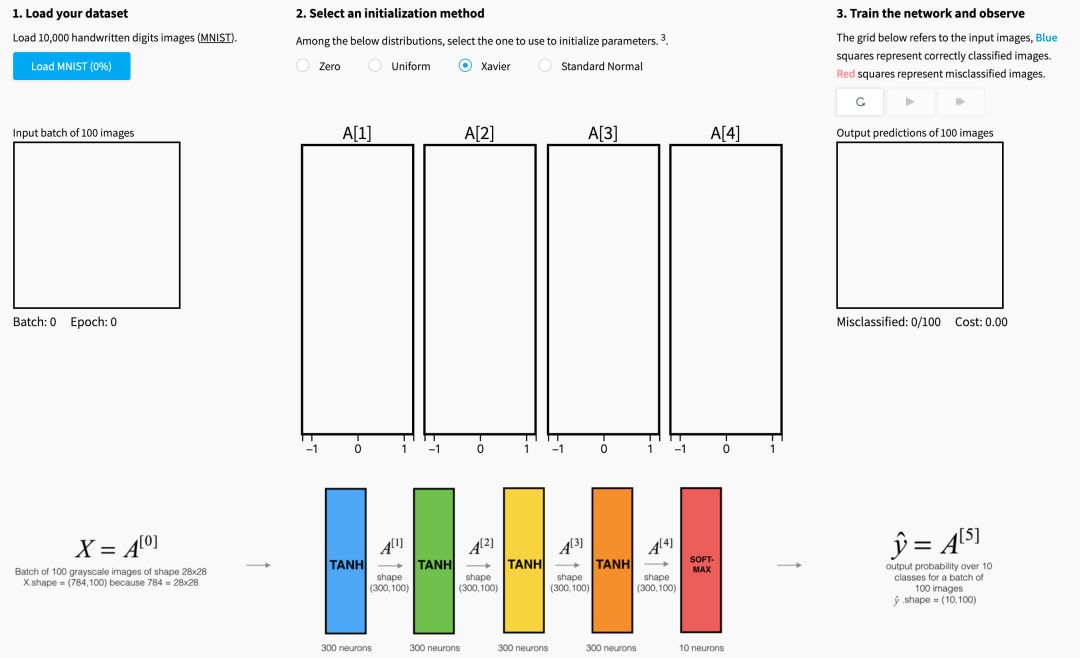
您可以在Glorot等人中找到這種可視化背后的理論。(2010年)。 下一節將介紹Xavier初始化的數學證明,并更準確地解釋為什么它是一個有效的初始化。
四、Xavier初始化的合理性
在本節中,我們將展示Xavier初始化使每個層的方差保持不變。 我們假設層的激活是正態分布在0附近。 有時候,理解數學原理有助于理解概念,但不需要數學,就可以理解基本思想。
讓我們對第(III)部分中描述的層l進行處理,并假設激活函數為tanh。 前向傳播是:
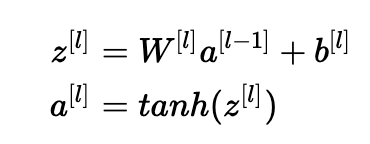
目標是導出Var(a [l-1])和Var(a [l])之間的關系。 然后我們將理解如何初始化我們的權重,使得:Var(a[l?1])=Var(a[l])。
假設我們使用適當的值初始化我們的網絡,并且輸入被標準化。 在訓練初期,我們處于tanh的線性狀態。 值足夠小,因此tanh(z[l])≈z[l],意思是:
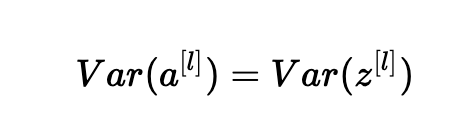
此外,z[l]=W[l]a[l?1]+b[l]=向量(z1[l],z2[l],…,zn[l][l])其中zk[l]=∑j=1n[l?1]wkj[l]aj[l?1]+bk[l]。 為簡單起見,我們假設b[l]=0(考慮到我們將選擇的初始化選擇,它將最終為真)。 因此,在前面的方程Var(a[l?1])=Var(a[l])中逐個元素地看,現在給出:
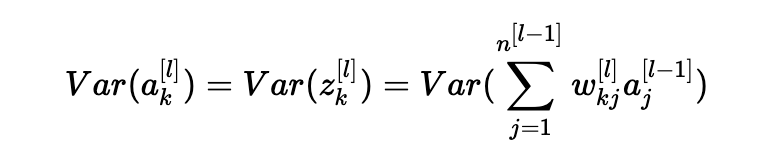
常見的數學技巧是在方差之外提取求和。 為此,我們必須做出以下三個假設:
1、權重是獨立的,分布相同;
2、輸入是獨立的,分布相同;
3、權重和輸入是相互獨立的。
因此,現在我們有:
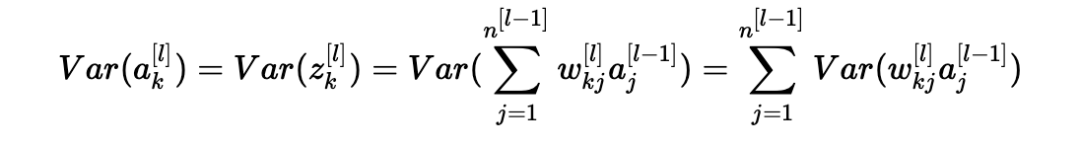
另一個常見的數學技巧是將乘積的方差轉化為方差的乘積。公式如下:
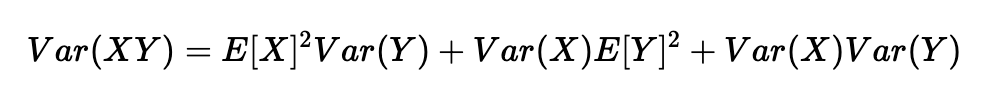
使用X=wkj[l]和Y=aj[l?1]的公式,我們得到:
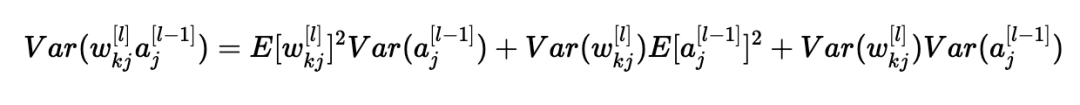
我們差不多完成了! 第一個假設導致E[wkj[l]]2=0,第二個假設導致E[aj[l?1]]2=0,因為權重用零均值初始化,輸入被歸一化。 從而:
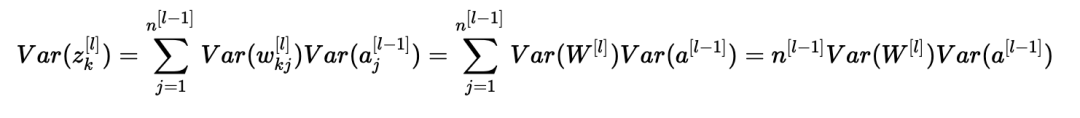
上述等式源于我們的第一個假設,即:
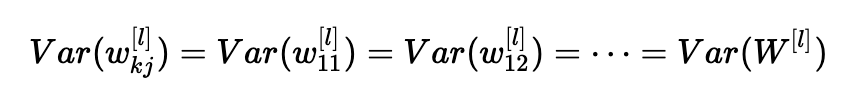
同樣,第二個假設導致:
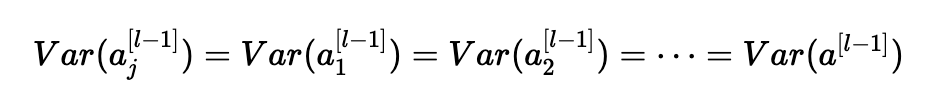
同樣的想法:
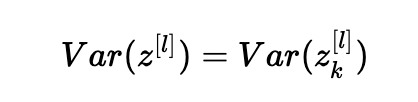
總結一下,我們有:
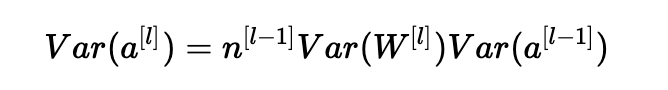
瞧! 如果我們希望方差在各層之間保持不變(Var(a[l])=Var(a[l?1])),我們需要Var(W[l])=n[l?1]1。 這證明了Xavier初始化的方差選擇是正確的。
請注意,在前面的步驟中,我們沒有選擇特定的層ll。 因此,我們已經證明這個表達式適用于我們網絡的每一層。 讓LL成為我們網絡的輸出層。 在每一層使用此表達式,我們可以將輸出層的方差鏈接到輸入層的方差:
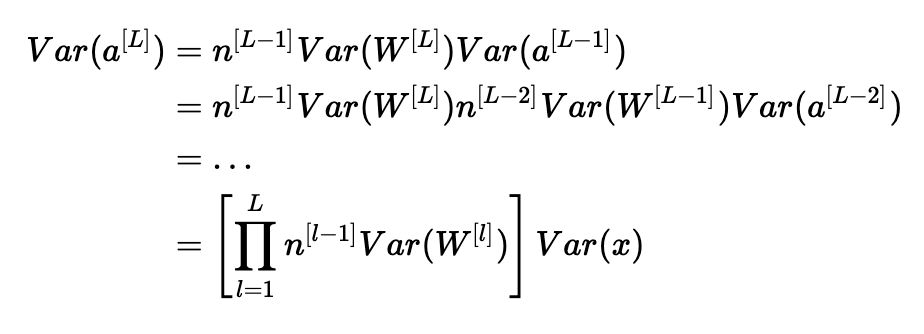
根據我們如何初始化權重,我們的輸出和輸入的方差之間的關系會有很大的不同。 請注意以下三種情況。
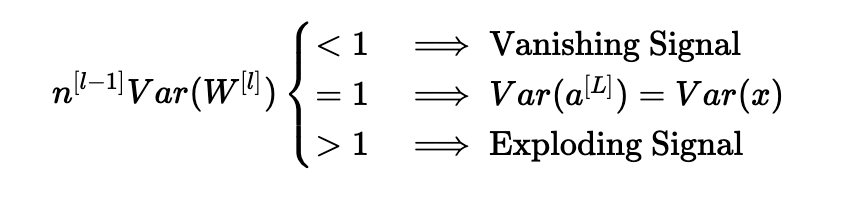
因此,為了避免正向傳播信號的消失或爆炸,我們必須通過初始化Var(W[l])=n[l?1]1來設置n[l?1]Var(W[l])=1。
在整個證明過程中,我們一直在處理在正向傳播期間計算的激活。對于反向傳播的梯度也可以得到相同的結果。這樣做,您將看到,為了避免梯度消失或爆炸問題,我們必須通過初始化Var(W[l])=n[l]1來設置n[l]Var(W[l])=1。
結論
實際上,使用Xavier初始化的機器學習工程師會將權重初始化為N(0,n[l?1]1)或N(0,n[l?1]+n[l]2)。 后一分布的方差項是n [l-1] 1和n [1] 1的調和平均值。
這是Xavier初始化的理論依據。 Xavier初始化與tanh激活一起工作。 還有許多其他初始化方法。 例如,如果您正在使用ReLU,則通常的初始化是He初始化(He et al,Delving Deep into Rectifiers),其中權重的初始化方法是將Xavier初始化的方差乘以2。雖然這種初始化的理由稍微復雜一些,但它遵循與tanh相同的思考過程。
-
神經網絡
+關注
關注
42文章
4779瀏覽量
101052 -
深度學習
+關注
關注
73文章
5512瀏覽量
121415
原文標題:吳恩達團隊:神經網絡如何正確初始化?
文章出處:【微信號:rgznai100,微信公眾號:rgznai100】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 神經網絡如何正確初始化?
神經網絡如何正確初始化?










評論