【導語】本文對傳統的人工數學建模和機器學習的優缺點進行了介紹和比較，并介紹了一種將二者優點相結合的方法——解耦表示學習。之后，作者利用 DeepMind 發布的基于解耦表示學習的 beta-VAE 模型，對醫療和金融領域的兩個數據集進行了探索，展示了模型效果，并提供了實驗代碼。

這篇文章會對傳統數學建模與機器學習建模之間的聯系進行討論。傳統數學建模是我們在學校里都學過的建模方法，該方法中，數學家們基于專家經驗和對現實世界的理解進行建模。而機器學習建模則是另一種完全不同的建模方式，機器學習算法以一種更加隱蔽的方式來描述一些客觀事實，盡管人類并不能夠完全理解模型的描述過程，但在大多數情況下，機器學習模型要比人類專家構建的數學模型更加精確。當然，在更多應用領域（如醫療、金融、軍事等），機器學習算法，尤其是深度學習模型并不能滿足我們需要清晰且易于理解的決策。

本文會著重討論傳統數學建模和機器學習建模的優缺點，并介紹一個將兩者相結合的方法 —— 解耦表示學習 (Disentangled Representation Learning)。

如果想在自己的數據集上嘗試使用解耦表示學習的方法，可以參考 Github 上關于解耦學習的分享，以及 Google Research 提供的關于解耦學習的項目代碼。

深度學習存在的問題

由于深度學習技術的發展，我們在許多領域都對神經網絡的應用進行了嘗試。在一些重要的領域，使用神經網絡確實是合理的，并且獲得了較好的應用效果，包括計算機視覺、自然語言處理、語音分析和信號處理等。在上述應用中，深度學習方法都是利用使用線性和非線性轉換對復雜的數據進行自動特征抽取，并將特征表示為“向量”（vector），這一過程一般也稱為“嵌入”（embedding）。之后，神經網絡對這些向量進行運算，并完成相應的分類或回歸任務：

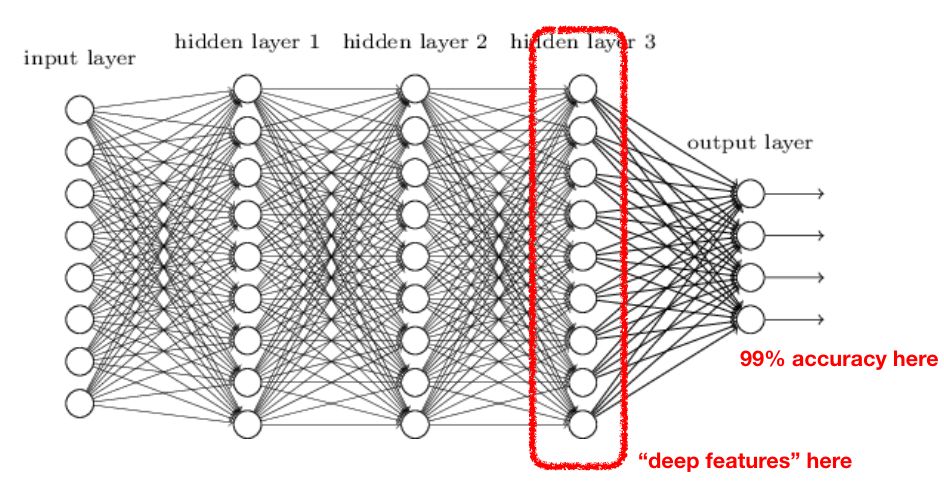
從特征提取和準確度來看，這種 “嵌入”的方法非常有效，但在許多方面也存在不足：

可解釋性：嵌入所使用的N維向量無法對模型分析的原理和過程進行很好的解釋，只有通過逆向工程才能找到輸入數據中對分析影響更大的內容。

數據需求量龐大：如果只有 10~100 個樣本，深度學習無法使用。

無監督學習：大多數深度學習模型都需要有標簽的訓練數據。

零樣本學習：這是一個很關鍵的問題，基于一個數據集所訓練出的神經網絡，若不經過重新訓練，很難直接應用在另一個數據集上。

對象生成：除了 GANs（生成對抗網絡）以外，其他模型都很難生成一個真實的對象。

對象操作：難以通過嵌入調整輸入對象的具體屬性。

理論基礎：雖然我們已經掌握了比較通用的逼近理論，但這還不夠。

這些問題很難用機器學習框架來解決，但在最近，我們取得了一些新的進展。

數學建模的優勢

在 20 年、50 年 甚至 100 年以前，大多數數學家都沒有遇到過上述問題。其中原因在于，他們主要關注數學建模（mathematical modeling），并通過數學抽象來描述現實世界中的對象和過程，如使用分布、公式和各種各樣的方程式。在這個過程中，數學家定義了我們在標題中提到的常微分方程（ordinary differential equations, ODE）。我們通過對比深度學習存在的問題，對數學建模的特點進行了分析。需要注意的是，在下面的分析中，“嵌入”代表數學模型的參數，如微分方程的自由度集合。

可解釋性：每個數學模型都是基于科學家對客觀事物的描述而建立的，建模過程包含數據家對客觀事物的描述動機和深入理解。例如，對于物理運動的描述， “嵌入” 包括物體質量、運動速率和坐標空間，不涉及到抽象的向量。

數據需求量大：大多數數學建模上的突破并不需要基于巨大的數據集進行。

無監督學習：對數學建模來說也不適用。

零樣本學習：一些隨機微分方程（如幾何布朗運動）可以應用于金融、生物或物理領域，只需要對參數進行重新命名。

對象生成：不受限制，對參進行采樣即可。

對象操作：不受限制，對參數進行操作即可。

理論基礎：上百年的科學基礎。

我們沒有使用微分方程解決所有問題的原因在于，對于大規模的復雜數據來說，微分方程的表現與深度學習模型相比要差得多，這也是深度學習得到飛速發展的原因。但是，我們仍然需要人工的數學建模。

將機器學習與基于人工的建模方法相結合

如果在處理復雜數據時，我們能把表現較好的神經網絡和人工建模方法結合起來，可解釋性、生成和操作對象的能力、無監督特征學習和零樣本學習的問題，都可以在一定程度上得到解決。舉個例子，視頻1中呈現的是對于人像的特征提取方法。

對于微分方程和其他人工建模方法來說，圖像處理很難進行，但通過和深度學習進行結合，上述模型允許我們進行對象的生成和操作、可解釋性強，最重要的是，該模型可以在其他數據集上完成相同的工作。該模型唯一的問題是，建模過程不是完全無監督的。另外，對于對象的操作還有一個重要的改進，即當我改變 ”胡須“ 這一特征時，程序自動讓整張臉變得更像男人了，也就是意味著，模型中的特征雖然具有可解釋性，但特征之間是相關聯的，換句話說，這些特征是耦合在一起的。

β -VAE

有一個方法可以幫助我們實現解耦表示，也就是讓嵌入中的每個元素對應一個單獨的影響因素，并能夠將該嵌入用于分類、生成和零樣本學習。該算法是由 DeepMind 實驗室基于變分自編碼器開發的，相比于重構損失函數（restoration loss），該算法更加注重潛在分布與先驗分布之間的相對熵。

若想了解更多細節，可閱讀beta-VAE的論文（https://openreview.net/forum?id=Sy2fzU9gl）；也可參考這個視頻2中的介紹，詳細解釋了 beta-VAE 的內在思想，以及該算法在監督學習和強化學習中的應用。

beta-VAE 可以從輸入數據中提取影響變量的因素，提取的因素包括物理運動的方向、對象的大小、顏色和方位等等。在強化學習應用中，該模型可以區分目標和背景，并能夠基于已有的訓練模型在實際環境中進行零樣本學習。

實驗過程

我主要研究醫療和金融領域的模型應用，在這些領域的實際問題中，上述模型能夠在很大程度上解決模型解釋性、人工數據生成和零樣本學習問題。因此在下面的實驗中，我使用 beta-VAEs 模型對心電圖（ETC）數據和和比特幣（BTC）的價格數據進行了分析。該實驗的代碼在 Github上可以找到。

首先，我使用veta-VAE（一個非常簡單的多層神經網絡）對PTB診斷數據中的心電圖數據進行了建模，該數據包含三類變量：心電圖圖表，每個人隨著時間變化的脈搏數據，以及診斷結果（即是否存在梗塞）。在 VAE 訓練過程中，epoch 大小設置為 50，bottleneck size 設置為 10，學習率為 0.0005，capacity 參數設置為 25（參數設置參考了這個GitHub項目）。模型的輸入是心跳。經過訓練，該模型學習到了數據集中影響變量的實際因素。

下圖展示了我使用其中一個單一特征對心跳數據進行操作的過程，其中黑線代表心跳，使用的特征數據值從 -3 逐漸增大至 3。在這一過程中，其他特征始終保持不變。不難發現，第 5 個特征對心跳形式的影響很大，第 8 個代表了心臟病的情況（藍色心電圖代表有梗塞癥狀，而紅色則相反），第 10 個特征可以輕微地影響脈博。

圖：對心電圖的心跳進行解耦

正如預期的一樣，金融數據的實驗效果沒有這么明顯。模型的訓練參數設置與上一實驗相似。使用的數據為 2017 年收集的比特幣價格數據集，該數據集包含一個時間長度為 180 分鐘的比特幣價格變化數據。預期的實驗效果為使用 beta-VAE 學習一些標準的金融時間序列模型，如均值回歸的時間序列模型，但實際很難對所獲得的表示進行解釋。在實驗結果中可以發現，第 5 個特征改變了輸入的時間序列的趨勢，第 2、4、6 個特征增加/減少了時間序列上不同階段的波動，或者說使其更加趨于穩定或動蕩。

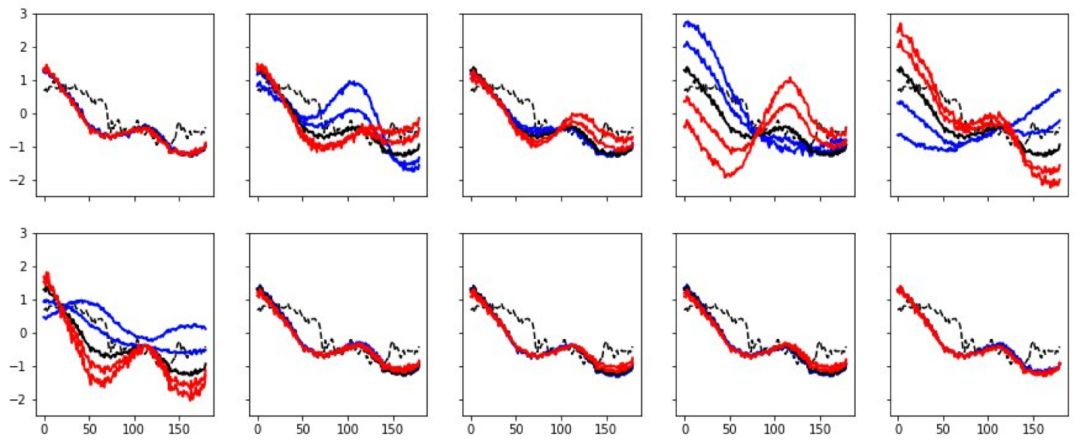
圖：對比特幣的收盤價格進行解耦

多個對象的解耦

假設在圖像中包含多個對象，我們想要找出每一個對象的影響因素。下面的動圖展示了模型的效果。

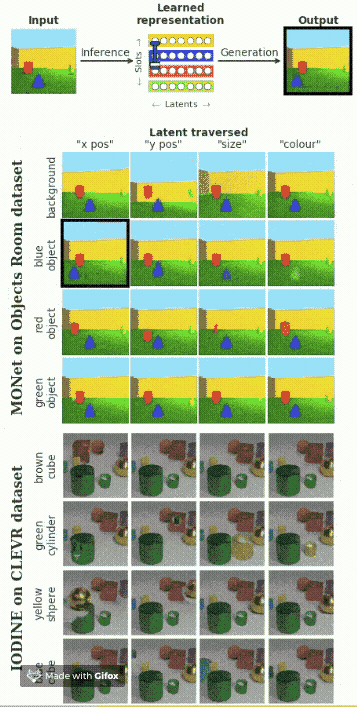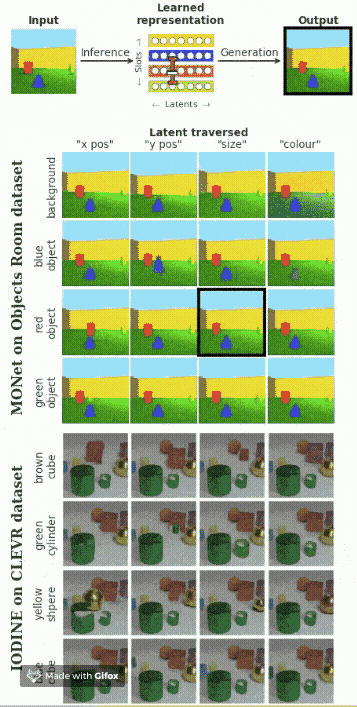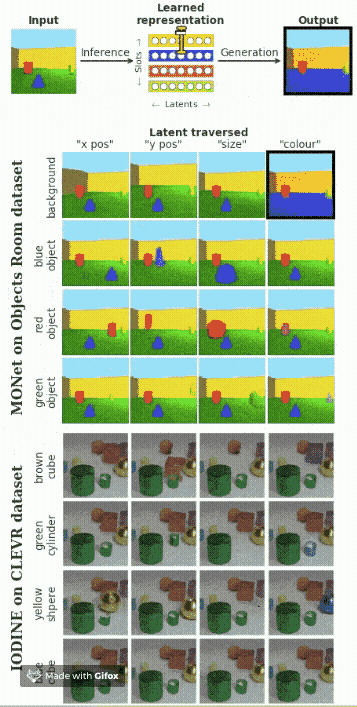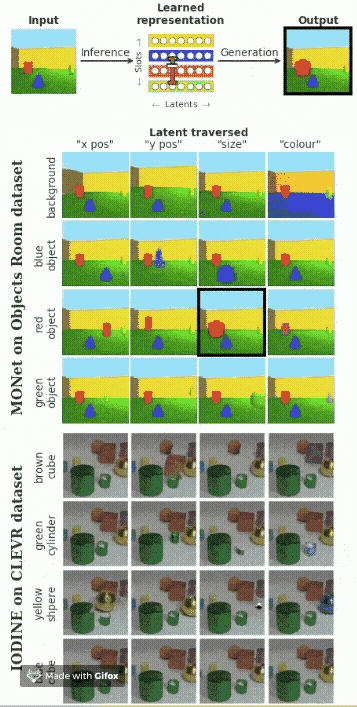
總結

下面針對于機器學習存在的問題列表對 beta-VAE 模型進行總結：

可解釋性：特征完全可解釋，我們只需要對每個具體嵌入的元素進行驗證。

數據需求量大：由于該模型屬于深度學習框架，數據需求量依然較大。

無監督學習：可以實現完全的無監督學習。

零樣本學習：可以進行，在文中展示的強化學習應用就屬于這一類。

對象生成：和普通的 VAE 一樣易于對參數進行采樣。

對象操作：可以輕松操作任何感興趣的變量。

理論基礎：有待研究。

上文的模型幾乎具備了數學建模的全部優質特性，也具有深度學習在分析復雜數據時的高準確度。那么，如果能使用完全無監督的方式，從復雜數據中學習到如此好的表示結果，是不是意味著傳統數學建模的終結？如果一個機器學習模型就可以對復雜模型進行構建，而我們只需要進行特征分析，那還需要基于人工的建模嗎？這個問題還有待討論。