Hi，大家好！我是至芯科技的李老師。

今天講課的題目比較有意思，它是一個小問題：把二進制變成BCD碼需要幾步？
請大家思考一下。有同學可能回答需要三步，為什么啊？
因為啊，把大象放進冰箱里需要三步，第一步，把冰箱門打開，第二步，把大象放進去，第三步，把冰箱門關(guān)上。
類似的，把二進制變成BCD碼，也需要三步。
blablablabla ......
當然啦，這是開玩笑了。不過，歪打正著，答案確實是三步。
究竟是怎么回事呢？我們下面細細說來，原理說透之后，我們演示一下具體的Verilog實現(xiàn)過程。

首先，看一下下面這張表格，把二進制（8’hFF）轉(zhuǎn)換為BCD（12’h255）的步驟列表。

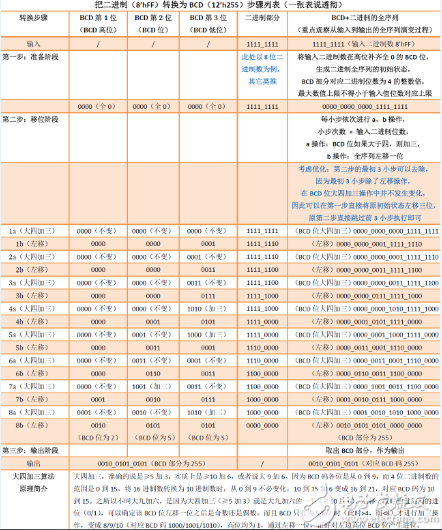
什么是二進制轉(zhuǎn)BCD？有什么用？

4位二進制是16進制數(shù)，而生活中常用的數(shù)制是10進制數(shù)。
怎么樣用計算機來理解、表達生活中的10進制數(shù)？這就需要進行16進制數(shù)與10進制數(shù)的相互轉(zhuǎn)換了。
而BCD碼（Binary-Coded Decimal）正是計算機常用的一種表達方式。
它是一種以二進制表示的十進制數(shù)碼。
比如說，至芯科技ZX-1開發(fā)板上的六位數(shù)碼管顯示數(shù)字可以是16進制的000000~FFFFFF，但是更為方便的方法是000000~999999。
六位數(shù)碼管顯示六位數(shù)字用十六進制，比如說是0F423F，誰也不知道是多少，但是它對應(yīng)的十進制數(shù)999999，大家肯定很熟悉。
很多場合，我們和機器之間溝通用10進制更方便，但計算機是用01編碼的。需要進行人機之間的溝通和轉(zhuǎn)換。
解決的方法就是用二進制的方式來存儲、計算數(shù)值，但是用10進制的方式來顯示這些數(shù)值，BCD碼就起到了橋梁的作用。
注意，16進制屬于二進制的一種形式，希望大家理解這點，包括8進制也是。

當然，道理容易明白。但究竟機器又是怎樣實現(xiàn)二進制和BCD碼的轉(zhuǎn)換的呢？
注意，轉(zhuǎn)換是雙向的，既可以把二進制轉(zhuǎn)換成BCD碼，也可以把BCD碼轉(zhuǎn)換成二進制數(shù)。
可以想象BCD碼轉(zhuǎn)成二進制相對比較簡單。
舉個例子吧，比如說BCD碼255，要轉(zhuǎn)換成二進制。
計算機里面存的BCD碼是12'h255（對應(yīng)二進制為12'b0010_0101_0101），肯定不能直接進行運算，必須要轉(zhuǎn)換成機器識別的二進制數(shù)值12'h0FF（對應(yīng)二進制為12'b0000_1111_1111）。
先算前兩位，直接2*10+5，得到結(jié)果25，然后再將結(jié)果*10+下一位，即25*10+5，最終結(jié)果為255，完了。
就這么簡單。當然這里255只有三位BCD位，如果更多的話，以此類推。
將前一步結(jié)果*10+下一位，得到當前結(jié)果。
當然實現(xiàn)起來還有一些小的技巧，x*10要占用乘法器資源，如果乘法器資源足夠那無所謂，但在資源有限的情況下通常用(x<<3)+(x<<1)（對應(yīng)x*8+x*2）來實現(xiàn)。
即用移位和加法來代替乘法操作。
當然也可以把BCD數(shù)字的每一位直接變成各種左移數(shù)值的組合，比如x*100 = x*64 + x*32 * x*4 = (x<<6) +( x<<5) + (x<<2)。
上面就是BCD碼轉(zhuǎn)成二進制的實現(xiàn)原理，這個比較簡單，我們這里略微帶過。

本課重點講解的是反過來怎么實現(xiàn)，即怎么把二進制轉(zhuǎn)換成BCD碼？
比如說，二進制數(shù)12'h0FF，要轉(zhuǎn)換成BCD碼255。
這個有點難，常見的做法是使用上圖中提到的大四加三算法。
當然你可以用查表法，比如說256以內(nèi)的數(shù)值，直接用查表的方式，一一對應(yīng)，就像我們FPGA采用LUT表實現(xiàn)真值表那樣，或者說用ROM表來根據(jù)不同輸入得到不同輸出。
這樣當然也是可以的，不過，它的范圍往往比較有限，不適于數(shù)量比較大的情況。

下面，我們就隆重有請本次課堂的主角——大四加三算法，隆重登場。

大四加三算法

如果前面那張表格，大家能看懂的話，我們就可以直入主題了。
從表中我們可以看到，把二進制變成BCD碼，也需要三步。

首先，明白問題的輸入和輸出要求，這是最起碼的，即輸入二進制數(shù)（比如8’hFF），要求輸出對應(yīng)的BCD碼（對應(yīng)為BCD碼12'h255）。
大四加三算法就是實現(xiàn)的過程。

第一步：準備階段。
我們將輸入二進制數(shù)在高位補齊全0的BCD位，生成二進制全序列的初始狀態(tài)。
BCD部分對應(yīng)二進制位數(shù)為4的整數(shù)倍，最大數(shù)值上限不得小于輸入值位數(shù)對應(yīng)上限。

第二步：移位階段。
第二步比較復(fù)雜。這一步分為多個小步，每小步將二進制全序列進行一次組合的左移操作。
之所以稱之為組合的左移操作，是因為包括一次移位的預(yù)操作（即BCD位大四加三）和單純的全序列左移操作。
具體這一步的操作過程，我們后面還會細講。
實際上大象那個比喻，也是第二步比較復(fù)雜。呵呵。
一旦原理明白了，我們編寫Verilog代碼想必也就水到渠成了。后面就是Verilog語言練習和具體實現(xiàn)的事了。

第三步：輸出階段。
這一步，最簡單，實際上第二步的最后環(huán)節(jié)已經(jīng)得出結(jié)果了，只不過它包含在全序列里面，我們只要取出需要的BCD部分，輸出即可。

大四加三算法原理簡介

我們再回到第二步上來，實質(zhì)上也是大四加三算法上來。
第一步、第三步就是準備和結(jié)束的階段，等同于打開冰箱門、關(guān)閉冰箱門。重點還是在于大象怎么放到冰箱里的。

第二步里面分為多個小步，每小步依次進行a、b操作，小步次數(shù) = 輸入二進制位數(shù)。
a操作：BCD位如果大于四，則加三。
b操作：全序列左移一位。

大四加三，準確的說是≥5加3，實質(zhì)上是≥10加6，或者說大9加6。
因為BCD碼各位是從0到9，而4位二進制數(shù)的范圍是0到15，將16進制數(shù)轉(zhuǎn)換為10進制數(shù)時，從0到9不必變化，10到15加6變成16到21，對應(yīng)BCD碼為10到15。
之所以不叫大九加六，是因為大四加三（≥5加3）就是大九加六的一半（≥10加6），左移一位時通過后面的進位（0/1），可以確定該BCD位左移一位之后是奇數(shù)還是偶數(shù)。
而且BCD只有為5/6/7時（此時>4，而<8）才進行加三操作，變成8/9/10（對應(yīng)BCD碼1000/1001/1010），高位均為1，通過左移一位，正好對左邊高位BCD位產(chǎn)生進位。

這樣說有點抽象，那張表格如果大家沒有一步步演變清楚的話，可以先弄清楚了。這樣有助于理解這個算法。
當然這個算法嚴謹?shù)淖C明過程肯定也是有的，李凡老師也提到過，有興趣的話可以深入鉆研一下。
這里，我們就先用歸納的方法，檢驗這種算法確實是能一步步將二進制數(shù)轉(zhuǎn)換成BCD碼。
表中輸入的是8位二進制數(shù)，位數(shù)更多，實質(zhì)上原理是一樣的，每位之間的遞進關(guān)系是2倍，每四位之間的遞進關(guān)系是16倍，你在增加位數(shù)，遞進的關(guān)系都是一樣的。
當然我們也可以自己推導(dǎo)一下12位二進制數(shù)，或者更多位，滿足一下我們的好奇心和求知欲。
就像圖示的表格一樣，只不過位數(shù)增加了而已。

本堂課要解決的課題

原理講過之后，我們要做一個更多位數(shù)的例子。
也就是開發(fā)板六位數(shù)碼管顯示的的問題，我們讓六位數(shù)碼管循環(huán)顯示十進制數(shù)000000~999999。

十進制數(shù)000000~999999在計算機里面，用于顯示實際上是BCD碼000000~999999，而用于計算處理則是二進制數(shù)20'h00000~20'hF423F（對應(yīng)20'd0~20'd99999）。
在循環(huán)顯示的時候，我們控制部分要對計數(shù)器進行加一操作，這時候是對二進制數(shù)進行操作。
在顯示輸出的時候，我們將二進制數(shù)轉(zhuǎn)換為BCD碼，輸出給數(shù)碼管進行顯示。這時候，就用到了二進制數(shù)轉(zhuǎn)換為BCD碼的操作，也就是大四加三算法。
所以說，這個例子對大四加三算法模塊的輸入輸出要求是，輸入20位的二進制數(shù)20'h00000~20'hF423F（對應(yīng)20'd0~20'd99999），要求輸出對應(yīng)的6位BCD碼000000~999999，對應(yīng)二進制位數(shù)是24位。
顯然這里的20位輸入24位輸出，比表格中的8位輸入12位輸出要多了很多，當然我們不是手工推導(dǎo)，而是要用FPGA來做，用Verilog代碼來建模。

b2bcd.v文件

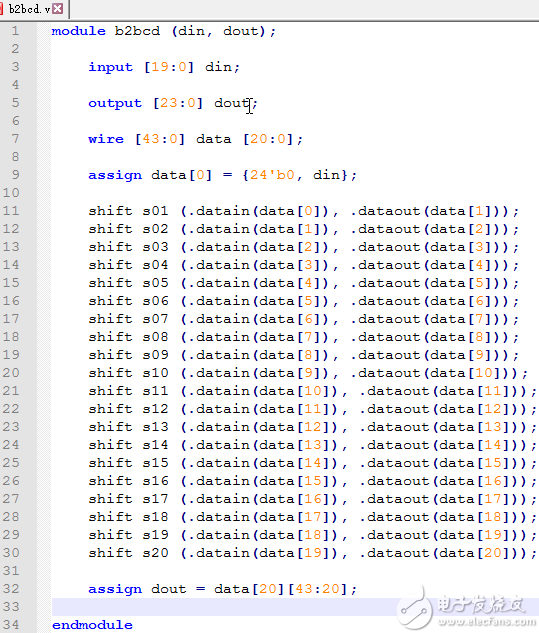
建模shift移位子模塊

shift移位子模塊shift.v文件如下：

module shift (datain, dataout);

input [43:0] datain;

output [43:0] dataout;

wire [43:0] data;

assign data[19:0] = datain[19:0];

preshift p0 (.d4in(datain[23:20]), .d4out(data[23:20])); //對應(yīng)第二步各小步下的a操作，此處為6個BCD位的大四加三操作。具體動作見preshift移位預(yù)操作子模塊。
preshift p1 (.d4in(datain[27:24]), .d4out(data[27:24]));
preshift p2 (.d4in(datain[31:28]), .d4out(data[31:28]));
preshift p3 (.d4in(datain[35:32]), .d4out(data[35:32]));
preshift p4 (.d4in(datain[39:36]), .d4out(data[39:36]));
preshift p5 (.d4in(datain[43:40]), .d4out(data[43:40]));

assign dataout = {data[42:0], 1'b0}; //對應(yīng)第二步各小步下的b操作，此處為全序列的左移移位操作。

endmodule

shift子模塊shift.v

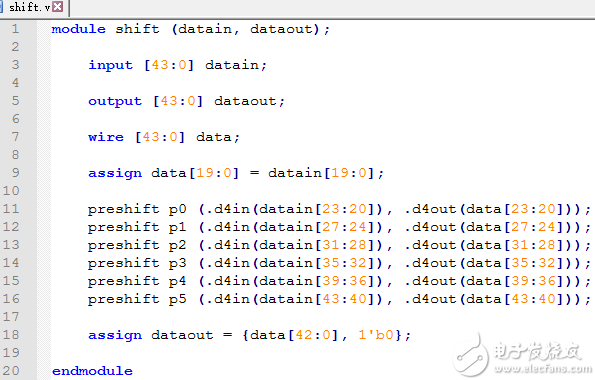
建模preshift預(yù)移位操作子模塊

preshift預(yù)移位操作子模塊preshift.v文件如下：

module preshift (d4in, d4out);

input [3:0] d4in;

output reg [3:0] d4out;

always @ (*)
begin
if (d4in > 4)
begin
d4out = d4in + 3; //如果大于四，則加三
end
else
begin
d4out = d4in; //如果不大于四，則不變
end
end

endmodule

preshift預(yù)移位操作子模塊preshift.v

preshift預(yù)移位操作子模塊，也可以這樣寫

module preshift (d4in, d4out);

input [3:0] d4in;

output [3:0] d4out;

assign d4out = (d4in > 4) ? d4in + 4'd3 : d4in; //如果大于四，則加三，否則不變。

// always (*)
// begin
// if (d4in > 4)
// begin
// d4out = d4in + 3;
// end
// else
// begin
// d4out = d4in;
// end
// end

endmodule

preshift預(yù)移位操作子模塊的另一種寫法

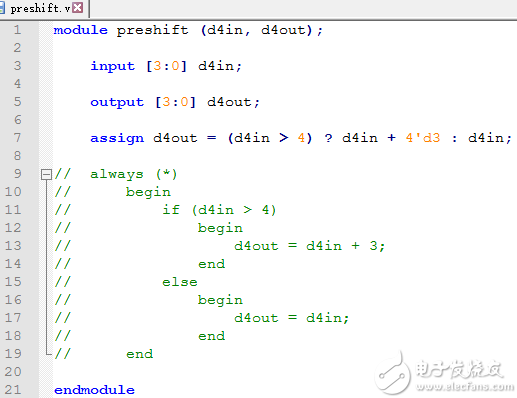
編寫Testbench模塊


Testbench模塊b2bcd_tb.v文件如下：

`timescale 1ns/1ps

module b2bcd_tb;

reg [19:0] din;

wire [23:0] dout;

integer i;

b2bcd dut (.din(din), .dout(dout));

initial
begin
din = 0;
for (i=0; i<=999999; i=i+1) #10 din = i; ? ? ? ? ? ? ? ?//六位數(shù)碼管循環(huán)顯示000000~999999

#100 $stop;
end

endmodule

Testbench模塊b2bcd_tb.v文件

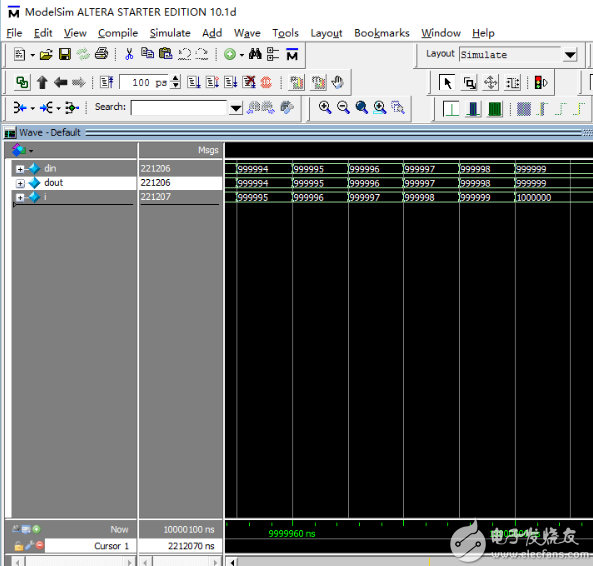
仿真運行結(jié)果

設(shè)置好仿真之后，可以看到仿真結(jié)果。
此時將din的數(shù)據(jù)格式設(shè)置為無符號數(shù)Unsigned，將dout的數(shù)據(jù)格式設(shè)置為十六進制數(shù)Hexadecimal。
可以看到兩種不同碼制的數(shù)據(jù)保持了完全一致。
從一個方面驗證了大四加三算法的正確性。

仿真運行結(jié)果圖示

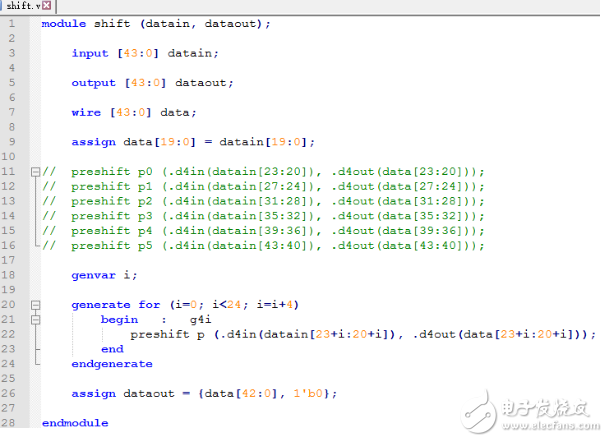
用generate for語句改寫shift移位子模塊shift.v文件

我們注意到由于存在重復(fù)性操作，相同的語句往往寫好多次。當然參數(shù)會稍微有所差異。
有個偷懶的辦法，就是采用generate for語句。
用generate for語句改寫的shift移位子模塊shift.v文件如下所示：

module shift (datain, dataout);

input [43:0] datain;

output [43:0] dataout;

wire [43:0] data;

assign data[19:0] = datain[19:0];

// preshift p0 (.d4in(datain[23:20]), .d4out(data[23:20]));
// preshift p1 (.d4in(datain[27:24]), .d4out(data[27:24]));
// preshift p2 (.d4in(datain[31:28]), .d4out(data[31:28]));
// preshift p3 (.d4in(datain[35:32]), .d4out(data[35:32]));
// preshift p4 (.d4in(datain[39:36]), .d4out(data[39:36]));
// preshift p5 (.d4in(datain[43:40]), .d4out(data[43:40]));

genvar i;

generate for (i=0; i<24; i=i+4)
begin : g4i
preshift p (.d4in(datain[23+i:20+i]), .d4out(data[23+i:20+i])); //對應(yīng)第二步各小步下的a操作，此處為6個BCD位的大四加三操作。具體動作見preshift移位預(yù)操作子模塊。
end
endgenerate

assign dataout = {data[42:0], 1'b0}; //對應(yīng)第二步各小步下的b操作，此處為全序列的左移移位操作。

endmodule

用generate for語句改寫的shift移位子模塊shift.v文件

用generate for語句改寫頂層模塊b2bcd.v文件

同樣的道理，我們對頂層模塊b2bcd.v文件的重復(fù)性語句也進行了改寫。
用generate for語句改寫的頂層模塊b2bcd.v文件如下所示：

module b2bcd (din, dout);

input [19:0] din;

output [23:0] dout;

wire [43:0] data [20:0];

assign data[0] = {24'b0, din}; //第一步：準備階段。將輸入二進制數(shù)在高位補齊全0的BCD位，生成二進制全序列的初始狀態(tài)。

genvar i;

generate for (i=0; i<20; i=i+1)
begin : g4i
shift s (.datain(data), .dataout(data[i+1])); //第二步：移位階段。依次進行20個小步操作。具體動作在shift子模塊中描述。
end
endgenerate

assign dout = data[20][43:20]; //第三步：輸出階段。取出BCD部分，作為輸出。

endmodule

第二步的小步次數(shù)優(yōu)化

前面表格中我們提到，第二步的最初3小步可以去除，因為最初3小步除了左移操作，在BCD位大四加三操作中并不發(fā)生變化。
因此可以在第一步直接將原初始狀態(tài)左移三位，原第二步直接跳過前3小步執(zhí)行即可。
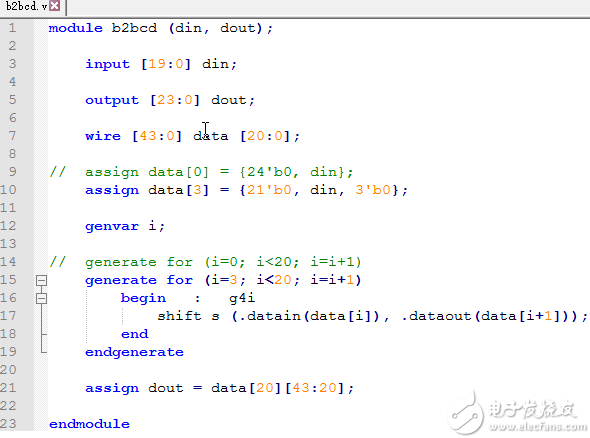
優(yōu)化結(jié)果體現(xiàn)在頂層模塊b2bcd.v文件中，如下所示：

module b2bcd (din, dout);

input [19:0] din;

output [23:0] dout;

wire [43:0] data [20:0];

// assign data[0] = {24'b0, din};
assign data[3] = {21'b0, din, 3'b0}; //第一步：準備階段。將輸入二進制數(shù)在高位補齊全0的BCD位，直接左移三位，生成二進制全序列的初始狀態(tài)。

genvar i;

// generate for (i=0; i<20; i=i+1)
generate for (i=3; i<20; i=i+1)
begin : g4i
shift s (.datain(data), .dataout(data[i+1])); //第二步：移位階段。依次進行17個（20-3）小步操作。具體動作在shift子模塊中描述。
end
endgenerate

assign dout = data[20][43:20]; //第三步：輸出階段。取出BCD部分，作為輸出。

endmodule

第二步的小步次數(shù)優(yōu)化結(jié)果體現(xiàn)在頂層模塊b2bcd.v文件中

查看RTL視圖——頂層模塊b2bcd.v


頂層模塊b2bcd.v的視圖如下所示。
其中最下面為全局視圖，上面為左邊、右邊的局部視圖，可以看到17個子步shift移位模塊逐次遞進的一個結(jié)果。

17個子步shift移位模塊逐次遞進的RTL視圖

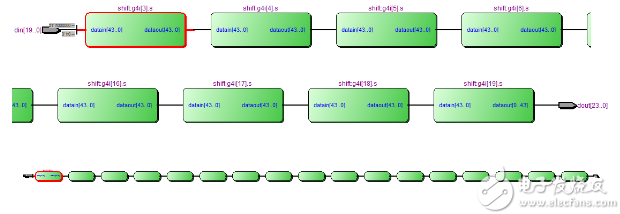
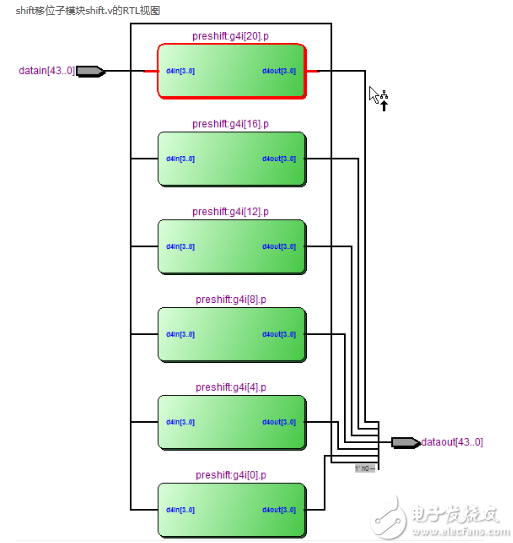
shift移位子模塊shift.v的RTL視圖如下。

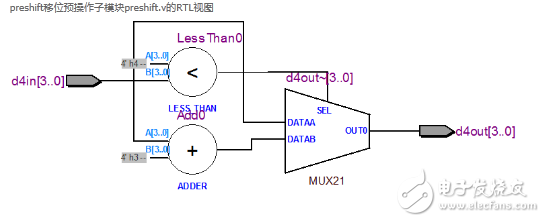
preshift移位預(yù)操作子模塊preshift.v的RTL視圖

?

加入數(shù)碼管驅(qū)動模塊seg7.v文件

為了更直觀地看到數(shù)碼管顯示效果，在已經(jīng)做好的工程文件中加入編寫好的數(shù)碼管驅(qū)動模塊seg7.v文件。
數(shù)碼管驅(qū)動模塊seg7.v文件如下所示。

module seg7 (clk, rst_n, data, sel, seg);

input clk, rst_n;
input [23:0] data;

output reg [2:0] sel;
output reg [7:0] seg;


reg [19:0] count;
reg clk_1ms;

always @ (posedge clk or negedge rst_n)
begin
if (!rst_n)
begin
clk_1ms <= 1;
end
else
begin
if (count < 24999)
begin
count <= count + 20'd1;
end
else
begin
count <= 0;
clk_1ms <= ~clk_1ms;
end
end
end


reg [2:0] state;
reg [3:0] data_temp;

always @ (posedge clk_1ms or negedge rst_n)
begin
if (!rst_n)
begin
sel <= 0;
data_temp <= 0;
state <= 0;
end
else
begin
case (state)
0 : begin
sel <= 0;
data_temp <= data[23:20];
state <= 1;
end

1 : begin
sel <= 1;
data_temp <= data[19:16];
state <= 2;
end

2 : begin
sel <= 2;
data_temp <= data[15:12];
state <= 3;
end

3 : begin
sel <= 3;
data_temp <= data[11:8];
state <= 4;
end

4 : begin
sel <= 4;
data_temp <= data[7:4];
state <= 5;
end

5 : begin
sel <= 5;
data_temp <= data[3:0];
state <= 0;
end

default : state <= 0;

endcase
end
end


always @ (*)
begin

if (!rst_n)
begin
seg = 8'b1111_1111;
end
else
begin
case (data_temp)
0 : seg = 8'b1100_0000; //d0
1 : seg = 8'b1111_1001; //d1
2 : seg = 8'b1010_0100; //d2
3 : seg = 8'b1011_0000; //d3
4 : seg = 8'b1001_1001; //d4
5 : seg = 8'b1001_0010; //d5
6 : seg = 8'b1000_0010; //d6
7 : seg = 8'b1111_1000; //d7
8 : seg = 8'b1000_0000; //d8
9 : seg = 8'b1001_0000; //d9
10 : seg = 8'b1000_1000; //dA
11 : seg = 8'b1000_0011; //db
12 : seg = 8'b1100_0110; //dC
13 : seg = 8'b1010_0001; //dd
14 : seg = 8'b1000_0110; //dE
15 : seg = 8'b1000_1110; //dF
default : seg = 8'b1000_1110; //dF
endcase
end
end

endmodule

創(chuàng)建新的頂層模塊top.v

創(chuàng)建新的頂層模塊top.v，循環(huán)生成要顯示的數(shù)字000000~999999，顯示數(shù)字每100ms更新一次，通過b2bcd模塊轉(zhuǎn)換成BCD碼，然后輸出給數(shù)碼管驅(qū)動模塊。
新的頂層模塊top.v文件如下所示。

module top (clk, rst_n, sel, seg);

input clk, rst_n;

output [2:0] sel;
output [7:0] seg;


reg [31:0] count;
reg [19:0] din;

wire [23:0] dout;

parameter T100ms = 5_000_000;

always @ (posedge clk or negedge rst_n)
begin
if (!rst_n)
begin
count <= 0;
din <= 0;
end
else
begin
if (count < T100ms - 1) ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?//顯示數(shù)字每100ms更新一次
begin
count <= count + 1;
end
else
begin

count <= 0;
if (din < 999999) ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?//循環(huán)生成要顯示的數(shù)字000000~999999
begin
din <= din + 20'd1;
end
else
begin
din <= 0;
end
end
end
end

b2bcd b2bcd
(
.din(din),
.dout(dout)
);

seg7 seg7
(
.clk(clk),
.rst_n(rst_n),
.data(dout),
.sel(sel),
.seg(seg)
);


endmodule

參照.tcl文件設(shè)置好FPGA管腳


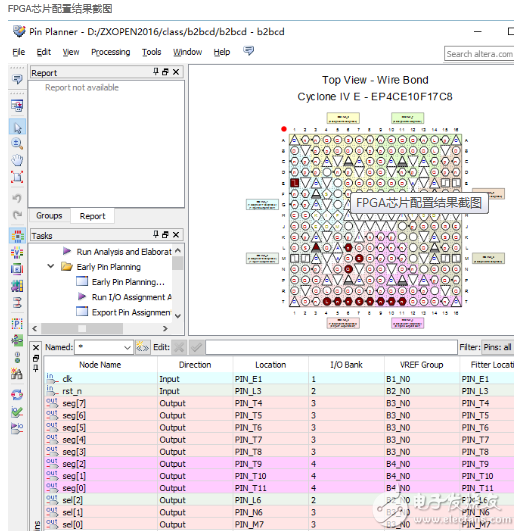
參照EP4CE10F17C8Nzx_1.tcl文件內(nèi)容，對FPGA芯片管腳進行設(shè)置。

EP4CE10F17C8Nzx_1.tcl文件相關(guān)內(nèi)容如下所示。FPGA芯片配置結(jié)果如圖所示。

#set_global_assignment -name FAMILY "Cyclone IV"
#set_global_assignment -name DEVICE ep4ce10f17c8n

set_location_assignment PIN_E1 -to clk

# KEY 輕觸按鍵
set_location_assignment PIN_L3 -to key[0]

# SEG7 x 8 七段數(shù)碼管
set_location_assignment PIN_L6 -to sel[2]
set_location_assignment PIN_N6 -to sel[1]
set_location_assignment PIN_M7 -to sel[0]
set_location_assignment PIN_T11 -to seg[0]
set_location_assignment PIN_T10 -to seg[1]
set_location_assignment PIN_T9 -to seg[2]
set_location_assignment PIN_T8 -to seg[3]
set_location_assignment PIN_T7 -to seg[4]
set_location_assignment PIN_T6 -to seg[5]
set_location_assignment PIN_T5 -to seg[6]
set_location_assignment PIN_T4 -to seg[7]

FPGA芯片配置結(jié)果截圖

.sof文件下載到FPGA


全編譯FPGA工程，生成.sof文件，連接至芯ZX-1開發(fā)板并上電。
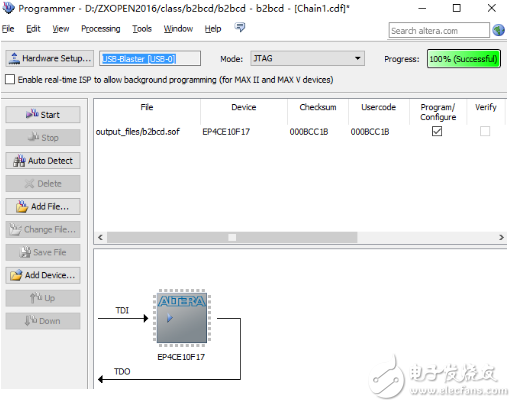
打開Programmer通過Jtag口，將.sof文件下載到FPGA進行在線仿真。
.sof文件下載界面如下圖所示。

開發(fā)板運行效果

開發(fā)板運行效果如下圖所示。
經(jīng)檢查，開發(fā)板運行效果與設(shè)計相符。

課程小結(jié)

本節(jié)課帶領(lǐng)大家學習了二進制轉(zhuǎn)換成BCD碼的原理，并使用Verilog實現(xiàn)大四加三算法的建模，結(jié)合六位數(shù)碼管顯示，在至芯ZX-1開發(fā)板上演示了程序結(jié)果。
希望大家通過本次課程的學習，掌握大四加三算法的原理，熟練編寫相關(guān)FPGA工程，掌握Verilog語法和相關(guān)開發(fā)工具。
課程到此結(jié)束，謝謝大家觀賞。