十進制轉換為二進制是計算機科學中非常基礎且重要的概念之一。在理解和應用計算機科學的基礎知識時,掌握這個算法是至關重要的。
在開始講解十進制轉換為二進制的算法之前,讓我們回顧一下十進制和二進制的基本原理。十進制數是我們日常生活中最常見的數字系統,它由0到9十個數字組成。而二進制是計算機科學中使用的數字系統,它只由0和1兩個數字組成。計算機內部操作的基本單位是位(bit),而以位(bit)為基礎的數字系統就是二進制。
現在我們進入正題,詳細討論十進制轉換為二進制的算法。這個算法可以通過一系列的步驟來實現,每個步驟都有其特定的目的。
首先,我們需要了解十進制數是如何轉換為二進制數的。在十進制數中,每一位的權值由2的冪決定。例如,最右邊的位的權值為2的0次冪(即1),接下來的位的權值為2的1次冪(即2),然后是2的2次冪(即4),依此類推。在二進制數中,每一位的權值也由2決定,但是每一位的權值是2的冪遞增的。最右邊的位的權值為2的0次冪(即1),接下來的位的權值為2的1次冪(即2),然后是2的2次冪(即4),然后是2的3次冪(即8),以此類推。
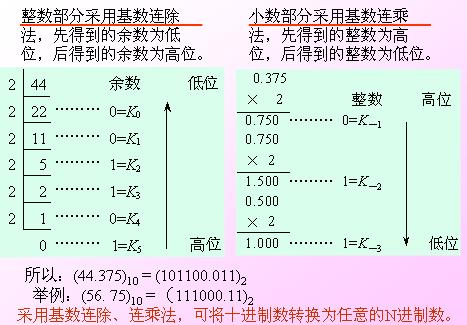
第一步是從十進制數的最右邊開始,逐個計算每一位的二進制值。我們需要將該位的值除以2,并將余數記錄下來。這個余數就是當前位的二進制值。如果余數為1,則表示該位為1;如果余數為0,則表示該位為0。
例子1:將十進制數10轉換為二進制數
我們先從最右邊的位開始,也就是10除以2。
10 ÷ 2 = 5,余數為0。所以最右邊的位為0。
現在我們需要繼續計算5的二進制值。我們再次將5除以2。
5 ÷ 2 = 2,余數為1。所以第二位為1。
最后,我們計算2的二進制值。我們再次將2除以2。
2 ÷ 2 = 1,余數為0。所以第三位為0。
最終結果為:10的二進制值為010。
例子2:將十進制數27轉換為二進制數
同樣,我們從最右邊的位開始,也就是27除以2。
27 ÷ 2 = 13,余數為1。所以最右邊的位為1。
現在我們需要繼續計算13的二進制值。我們再次將13除以2。
13 ÷ 2 = 6,余數為1。所以第二位為1。
然后我們計算6的二進制值。我們再次將6除以2。
6 ÷ 2 = 3,余數為0。所以第三位為0。
最后,我們計算3的二進制值。我們再次將3除以2。
3 ÷ 2 = 1,余數為1。所以第四位為1。
最終結果為:27的二進制值為11011。
通過以上兩個例子,我們可以看到,十進制數轉換為二進制數的關鍵是不斷地將當前位的值除以2,并記錄下余數。同時,我們需要從最右邊的位開始計算,并逐個向左移動。
接下來,我們來討論一些特殊情況。在某些情況下,十進制數的二進制表示可能會產生一個很長的二進制值。這是因為某些十進制數可能不是2的冪的倍數。在這種情況下,我們仍然使用上述算法,但我們只需要保留我們需要的位數,而忽略其他位數。
例子3:將十進制數15轉換為二進制數
同樣,我們從最右邊的位開始,也就是15除以2。
15 ÷ 2 = 7,余數為1。所以最右邊的位為1。
現在我們需要繼續計算7的二進制值。我們再次將7除以2。
7 ÷ 2 = 3,余數為1。所以第二位為1。
然后我們計算3的二進制值。我們再次將3除以2。
3 ÷ 2 = 1,余數為1。所以第三位為1。
最后,我們計算1的二進制值。我們再次將1除以2。
1 ÷ 2 = 0,余數為1。所以第四位為1。
最終結果為:15的二進制值為1111。
在此過程中,我們可以看到最終的結果為四位二進制數,而沒有使用其他位數。
在計算機科學中,我們經常需要將十進制數轉換為二進制數。無論是在編程中還是在計算機內部的計算過程中,這個算法都起著極其重要的作用。理解這個算法可以幫助我們更好地理解計算機內部的工作原理,并能夠更好地應用這些基礎知識。
總結起來,將十進制數轉換為二進制數的算法可以通過一系列的步驟來實現。首先,我們需要將當前位的值除以2,并記錄下余數。然后,我們將商作為下一步的被除數,并重復上述過程,直到商為0為止。最后,我們將所記錄的余數從最右邊的位開始,按照從右到左的順序排列,并得到最終的二進制值。
-
二進制
+關注
關注
2文章
795瀏覽量
41661 -
計算機
+關注
關注
19文章
7500瀏覽量
88017 -
數字系統
+關注
關注
0文章
143瀏覽量
20852 -
10進制
+關注
關注
0文章
6瀏覽量
7265
發布評論請先 登錄
相關推薦
二進制電平,什么是二進制電平
二進制如何轉換為十進制?
浮點數轉換為二進制存儲





 10進制轉換為二進制的算法
10進制轉換為二進制的算法

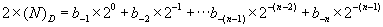










評論