無論是merge還是rebase,都是在同一個工作目錄中協調差異,處理變更歷史。而git的另一些命令,允許開發者單獨保存,或者通過文件或郵件的方式與別人分享這些差異。
這有助于更靈活的選擇和使用某些較為獨立的更改。這有點類似另一類版本控制系統的工作方式:存儲差異而不是快照。
可以使用 git diff > patchfile 將差異輸出到patch文件,保存或者分享給他人。使用 git diff 命令可以查看工作區修改的內容,git diff —cached 命令查看添加到暫存區但還未提交的內容。這兩種命令會生成兼容unix系統的標準格式patch。類似這樣:
git apply --stat patchfile
git apply --check patchfile
git apply patchfile
這三條命令分別是,檢查patch文件格式,測試patch是否能應用到當前分支,應用此patch。
這種方式傳遞的修改將會丟失提交信息和作者信息,但可以兼容非git管理的代碼。除此之外,git還提供另一個命令更便于git庫之間的patch傳遞。
git format-patch commit-id
git format-patch -s commit-id
生成指定提交之后的所有提交的patch。把 -s 改為 -n,n為任意數字,則會生成每個提交之前的n個patch。每個patch是單獨的文件,命名類似于:
0001-commit message.patch
format-patch生成的patch保存了更多提交信息。因此除了git apply之外,還可以用更智能的git am命令使用此patch。git am 命令會在應用patch失敗時給出詳細的錯誤信息,并允許手動解決沖突,是官方較為推薦的補丁應用方式。
我們在使用版本控制工具時,總會花費很多時間來處理diff,比如檢查正在進行的未提交的工作,查看單個提交中發生了什么變更,在執行合并之前比較兩個分支,等等。
diff是版本控制的核心概念,但可能大多數使用者沒有考慮過它是如何生成的。請思考一下如何編寫一個函數來計算diff。很容易發現,更準確的需求是只顯示發生了什么變化,忽略其他保持不變的部分。那么,如何確定文件的哪些部分沒有更改?如果從某行開始發現了差異,如何在每個版本中找到再次匹配的部分?
對修改者來說,哪些東西應該標記為更改似乎是顯而易見的。比如向文件中插入新代碼、刪除冗余語句或重寫部分函數,作為代碼的貢獻者,我們總會有一個直觀的心理模型。然而,如同大多數程序員所知,只會執行指令的機器要得到一個符合人類直覺的結果,通常比看上去要困難的多。而且總會存在很多可供選擇的實現方法,會產生完全不同的結果。
例如:有原序列ABCABBA,記做a,長度記為N,修改后的序列CBABAC,記做b,長度記為M。以單個字符為最小單位,把刪除和添加兩個步驟作為變更的基本操作。從a到b顯然有很多種方法,比如可以直接簡單粗暴的刪除a,再添加b,那么編輯腳本看起來會是這樣:
一共需要 N+M 步,這顯然不是我們想要的最簡操作。再繼續觀察,發現操作中出現了對同一個字符的刪除和新增操作,這些字符可以看做不變的部分,省略編輯步驟。
但是又出現了新的問題,比如僅看新串的前三個字符CBA,它可以看做原串第3-7字符刪掉中間AB,也可以看做2-4字符的前面加C同時刪除中間的C。這兩者雖然步數相同,但不同的看待方式會影響其他字符的變更步數。另外,就算全部步數相同,也可能存在一些方式比另一些方式更直觀更容易理解。
形式上,問題的關鍵是找到一個最長公共子序列,或者等價地,找到將一個序列轉換成另一個序列的符號的最少步驟。這是一個已有廣泛研究基礎的問題,git使用的默認算法由Eugene W. Myers 在1986年的論文(http://www.xmailserver.org/diff2.pdf)中提出。
Myers的算法就是這樣一種策略,它的速度很快,而且它產生的變更大部分情況下都是最直觀的。它通過貪心的方式來實現這一點,即優先嘗試使用相同的行數,并且在處理等價步驟時優先選擇刪除而不是插入。
下面嘗試較為直觀的展示該算法的基本步驟,并通過一個示例表現它如何計算從一個版本到另一個版本的最簡變更。
令x軸為原序列a,y軸為新序列b,兩個序列之間的轉換就可以表示為下圖。向右表示刪除一個字符,而向下則表示新增,對角邊對應那些允許不變的部分。
原問題就轉化為找從點(0,0)到點(N,M)的最多對角邊,同時也等于找從點(0,0)到點(N,M)的最少非對角邊。對應更少變更操作的要求,設置對角邊的權值為0,非對角邊的權值為1。這樣,問題也等價于在圖中找一條從點(0,0)到(N,M)的權值最小的路徑,屬于單源最短路問題的一個特例。
下面引入幾個概念:
D:待求得的最小權值,也就是原問題中的最小操作步數。(取值范圍從0到MAX,MAX = M+N)
k :k = x - y,使用橫縱坐標的差來標記對角線,無論線上是否存在對角邊。它的范圍是從-M到N。
snake :連續的對角邊序列(可以為空,為空時即等于終止點)
D-path:用來表示一個權重數為D的路徑,也就是水平垂直邊數為D的路徑。比如D=0的0-path就是一條只有對角邊的路徑。基于對角線的概念,任意D-path的結束點都會在某個k值對應的對角線上。
這里比較容易混淆的概念就是對角線和對角邊,對應到上圖,對角線指的是穿過所有點,公式為 x=y+k 的一系列等距斜線。而對角邊或snake僅表示那些連接相同字符的實線線段。如下圖:
一條D-path的終止點,所在的對角線的k值和D的差一定是偶數,并且范圍在-D和D之間。基于這些概念,原論文中先論證了兩條理論:
若一條D-path的最遠結束點對應的對角線為k,那么最遠的(D-1)-path必然達到了對角線 k±1 。
第一條很容易理解,參照上圖,構思一個D=3的D-path,會發現它的終止點不可能在-2,0,2這些k值對應的線上。
第二條基于上一條結論,(D-1)-path或(D+1)-path必定會和D-path相差一條水平或垂直邊,必然會導致 k值有±1的變動。
基于這兩個結論,論文作者給出一種時間復雜度O((M+N)D)的貪心算法。基本步驟如下:
讓步數D從0開始增長,最大值為MAX。
對應每個D值,讓k從-D到D以步數為2增長。在圖上體現為從右上向左下依次循環。
對每個D值的所有k值,保存或更新對應D-path達到的最大x坐標。這保證了D-path優先向右延伸,即優先刪除。
隨著循環進行,D值不斷增長,D-path不斷延伸,直到 x >= N 并且 y >= M,說明最遠D-path的終止點已經可以到達終點(N,M),算法終止。
文中的偽代碼如下:
整個步驟也可以表示為下圖,其中(0,-1)的虛擬點和超出圖范圍的部分,是處于遍歷中邊界條件的需要,把終止點為(0,0)和全圖不含對角邊的情況包含其中。
對于最開始舉的例子,可以找到的最佳diff路徑類似這樣:
現在結合上面的偽代碼詳述一下計算過程:
循環D=0:
k=0。根據if條件k = -D,和預先賦值的V[1] = 0,待判定點的x設置為0。
第8行,y=x-k=0。
第9行判斷是否存在(0,0)->(1,1)的對角邊,不存在這個邊,所以不變更終止點。
第10行保存D=0,k=0時的最大x坐標值:V[0] = 0。
第一輪D=0結束時,唯一最遠終止點為(0,0)
循環D=1:
k取值-1或1。分別對應上圖D=1時與橫縱軸相交的兩個點。
k = -1,滿足條件 k=-D,所以 x =V[0] = 0, y = x-k = 1。而(0,1)->(1,2)不存在對角邊。
記錄D=1,k=-1時的x值,V[-1] = 0。
k = 1,不滿足第4行的條件,跳轉到第7行,x = V[0] + 1 = 1, y = x-k = 0。
記錄D=1,k=1的x值,V[1] = 1。
第二輪D=1結束時,達到過的最遠終止點為(1,0)和(0,1)。
但因為V數組僅保存最大x坐標,以實現優先刪除,記錄最遠終止點為(1,0)
此時 V[-1] = 0, V[0] = 0, V[1] = 1
循環D=2:
k取值-2,0,2。
k = -2,滿足條件 k=-D,設置 x =V[-1] = 0, y = x-k = 2。
第9行循環判斷,(0,2)->(1,3)->(2,4)存在連續對角邊。所以此條件下終止點為(2,4)。
記錄D=2,k=-2時的x值,V[-2] = 2。
k = 0,判斷第4行”or”之后的條件,V[-1] < V[1],即 0 < 1,成立。設置 x = 1,y = x-k = 1。
此點存在對角邊(1,1)->(2,2),記錄D=2,k=0時的x值,V[0] = 2。
k = 2,不滿足第4行條件,執行第7行設置 x = V[1]+1 = 2,y = x-k = 0。
此點存在對角邊(2,0)->(3,1),記錄D=2,k=2時的x值,V[2] = 3。
此輪D=2結束時,達到過的最遠終止點為(2,4)(2,2)和(3,1)。
V數組僅保存最大x坐標,所以記錄最遠終止點為(3,1)。
以下依次循環,直到足以到達(N,M)點。
細心的讀者可能會發現,以上步驟僅保存了最遠終止點及對應D值,為了明確列出具體路徑,還需要保存每一步的終止點和方向,這還需要額外O(D*D)的空間復雜度。于是作者繼續提出一種優化方案。
方案基于作者提出的第三條理論:
從序列a到序列b的最佳D-path,與b到a的最佳D-path,必然重合(或翻轉重合)在最佳的終止點或snake對角邊上。
作者針對這一理論給出了詳細論證。因為作者也沒太讀懂公式,有興趣可以繼續查閱原論文。
這一優化方式把上一部分的單向搜索,轉化為從起點和終點向中間搜索公共snake的問題。只要找到一對相反并且同時達到最遠的重合路徑,就可以停止并輸出這個snake或終止點。最差情況需計算兩條D-path,這對時間復雜度影響不大。
優化后的算法采用二分法遞歸查找最佳路徑,只需要線性的存儲空間,和O((M+N)D)的時間復雜度。這對于較大數據量的對比十分有利。是git和unix系統共同采用的diff方式。
-
存儲
+關注
關注
13文章
4347瀏覽量
86058 -
Git
+關注
關注
0文章
201瀏覽量
15797
發布評論請先 登錄
相關推薦
git命令的基本使用
Git命令之本地分支與遠程分支關聯和解除

git shell 常用命令
git rebase與相關git merge命令比較
git的命令和參數
Git命令的綜合手冊怎么找
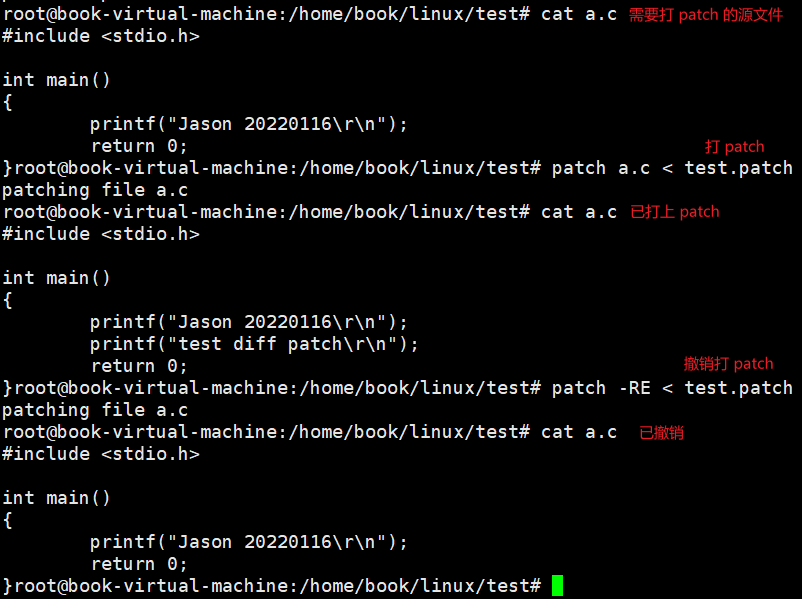
如何在Linux下打patch(下)
git基本操作命令用法
Git中的最常用命令詳解
Git中最常用的命令介紹




 Git命令解析-patch、apply、diff
Git命令解析-patch、apply、diff











評論