前言

之前通過線上課程學習David Silver的《強化學習》，留下深刻印象的是其中一堆堆的公式。公式雖然嚴謹，但是對于我來說，遇到實際問題時，我需要在腦海中浮現出一幅圖或一條曲線，幫我快速定位問題。正所謂“一圖勝千言”嘛。

最近終于找到了這樣一幅圖。國外有大神用漫畫的形式講解了強化學習中經典的Advantage-Actor-Critic（A2C）算法。盡管標題中只提及了A2C，實際上是將整個RL的算法思想凝結在區區幾幅漫畫中。

我很佩服漫畫的作者，能夠從復雜的公式中提煉出算法的精髓，然后用通俗易懂、深入淺出的方式展示出來。能夠將厚書讀薄，才能顯現出一個人的功力。

有這樣NB的神作，不敢獨吞，調節一下順序，補充一些背景知識，加上我自己的批注，分享出來，以饗讀者。 原漫畫的地址見：Intuitive RL: Intro to Advantage-Actor-Critic (A2C)，英語好的同學可以科學上網看原版的。

基本概念

強化學習中最基礎的四個概念：Agent, State, Action, Reward

Agent：不用多說，就是你的程序，在這里就是這只狐貍。

Action: agent需要做的動作。在漫畫中，就是狐貍在岔路口時，需要決定走其中的哪一條路。

State: 就是agent在決策時所能夠掌握的所有信息。對于這只狐貍來說，既包括了決策當時的所見所聞，也包括了它一路走來的記憶。

Reward：選擇不同的路，可能遇到鳥蛋（正向收益），也有可能遇到豺狼（負向收益）。

為什么Actor? 為什么Critic?

正如我之前所說的，Actor-Critic是一個混合算法，結合了Policy Gradient（Actor）與Value Function Approximation (Critic)兩大類算法的優點。原漫畫沒有交待，一個agent為什么需要actor與critic兩種決策機制。所以，在讓狐貍繼續探險之前，有必要先簡單介紹一下Policy Gradient （策略梯度，簡稱PG）算法，后面的內容才好理解。

Policy Gradient看起來很高大上，但是如果類比有監督學習中的多分類算法，就很好理解了。兩類算法的類比（簡化版本）如下表所示，可見兩者很相似

“分類有監督學習”與“策略梯度強化學習”的對比

還是以狐貍在三岔路口的選擇為例

N就是樣本個數

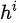就是每次決策前的信息，即特征

如果選擇哪條岔道是有唯一正確答案的，并且被標注了，即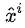?，則我們可以用“多分類算法”來學習它。

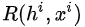但是，在強化學習中，每次選擇沒有唯一正確的答案，而且每次選擇的收益也是延后的。既然我們不知道所謂“唯一正確答案”，我們就做一次選擇?(未必是最優的)，再將這個選擇對最終loss或gradient的貢獻乘以一個系數，即上式中的?，有個學術的名字叫“Likelihood Ratio”

怎么理解Likelihood Ratio這個乘子？這個乘子必須滿足什么樣的要求？最簡單的形式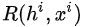，?可以是一次實驗（如AlphaGo的一次對弈，狐貍一天的探險）下來的總收益。從而PG可以寫成如下形式：

Policy Gradient公式

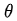是優化變量

公式左邊是平均收益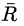

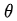
公式右邊中，N是總實驗的次數，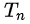

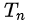
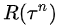是第n次實驗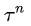

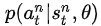是第n次實驗中，第t步時，在當前state是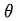的概率的情況下，選擇了動作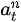

以上公式表明：

如果第n次實驗的總收益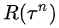是正的，則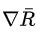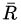假定第n次實驗中的每步決策都是正確的，應該調節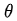

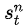
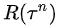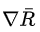
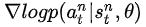
如果第n次實驗的總收益是負的，則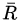假定第n次實驗中的每步決策都是錯誤的，應該調節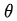

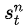
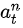
基于“真實有效的決策，在成功實驗出現的次數，比在失敗實驗出現的次數，要多”這樣的假設，以上方法還是能夠學到東西的。

但是，以上算法中統一用做乘子，還是太簡單粗暴，有些“一榮倶榮，一損俱損”搞“連坐”的味道。因此，在實際算法中，圍繞著policy gradient前的那個乘子，衍生出多種變體，

比如考慮每步決策的直接收益的時間衰減，就是REINFORCE算法。

如果用V(S)，即“狀態值”state-value，來表示PG前的系數，并用一個模型來專門學習它，則這個擬合真實（不是最優）V(s)的模型就叫做Critic，而整個算法就是Actor-Critic算法。

因為篇幅所限，簡單介紹一下V(s)與Q(s,a)。它們是Value Function Approximation算法中兩個重要概念，著名的Deep Q-Network中的Q就來源于Q(s,a)。V(s)表示從狀態s走下去能夠得到的平均收益。它類似于咱們常說的“勢”，如果一個人處于“優勢”，無論他接下去怎么走（無論接下去執行怎樣的action），哪怕走一兩個昏招，也有可能獲勝。具體精確的理解，還請感興趣的同學移步David Silver的課吧。

重新回顧一下算法的脈絡，所謂Actor-Critic算法

Actor負責學習在給定state下給各候選action打分。在action空間離散的情況下，就類似于多分類學習。

因為與多分類監督學習不同，每步決策時，不存在唯一正確的action，所以PG前面應該乘以一個系數，即likelihood ratio。如果用V(S)，即state-value，來表示PG前的乘子，并用一個模型來專門學習它，則這個擬合V(s)的模型就叫做Critic，類似一個回歸模型。

如果用Critic預測值與真實值之間的誤差，作為likelihood ratio，則PG前的乘子就有一個專門的名稱，Advantage。這時的算法，就叫做Advantage-Actor-Critic，即A2C。

如果在學習過程中，引入異步、分布式學習，此時的算法叫做Asynchronous-Advantage-Actor-Critic，即著名的A3C。

狐貍的探險

上一節已經說明了狐貍(Agent)為什么需要actor-critic兩個決策系統。則狐貍的決策系統可以由下圖表示

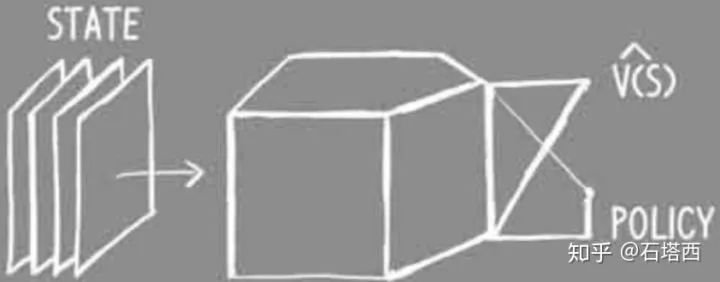
state是狐貍做決策時所擁有的一切信息，包括它的所見所聞，還有它的記憶。

critic負責學習到準確的V(s)，負責評估當前狀態的“態勢”，類似一個回歸任務。

actor負責學習某狀態下各候選action的概率，類似一個多分類任務。

在第一個路口

狐貍的critic覺得當前態勢不錯，預計從此走下去，今天能得20分，即V(s)=20

狐貍的actor給三條路A/B/C都打了分

狐貍按照A=0.8, B=C=0.1的概率擲了色子，從而決定走道路A（沒有簡單地選擇概率最大的道路，是為了有更多機會explore）

沿A路走，采到一枚蘑菇，得1分

把自己對state value的估計值，采取的動作，得到的收益都記錄下來

在接下來的兩個路口，也重復以上過程：

狐貍的反思：更新Critic

畢竟這只狐貍還太年輕，critic對當前狀態的估計可能存在誤差，actor對岔道的打分也未必準確，因此當有了三次經歷后，狐貍停下來做一次反思，更新一下自己的critic和actor。狐貍決定先更新自己的critic。

之前說過了，critic更像是一個“回歸”任務，目標是使critic預測出的state value與真實state value越接近越好。以上三次經歷的state value的預測值，狐貍已經記在自己的小本上了，那么問題來了，那三個state的真實state value是多少？

在如何獲取真實state value的問題上，又分成了兩個流派：Monte Carlo(MC)法與Temporal-Difference(TD)法。

MC法，簡單來說，就是將一次實驗進行到底，實驗結束時的V(s)自然為0，然后根據Bellman方程回推實驗中每個中間步驟的V(s)，如下圖所示（圖中簡化了Bellman方程，忽略了時間衰減）。MC法的缺點，一是更新慢，必須等一次實驗結束，才能對critic/actor進行更新；二是因為V(s)是狀態s之后能夠獲得的平均收益，實驗越長，在每個步驟之后采取不同action導致的分叉越多，但是MC法僅僅依靠上一次實驗所覆蓋的單一路徑就進行更新，顯然導致high variance。

Monte Carlo法

另一種方法，TD法，就是依靠現有的不準確的critic進行bootstrapping，逐步迭代，獲得精確的critic

現在狐貍要反思前三個狀態的state value，狐貍假定當前critic（老的，尚未更新的）在當前狀態（第4個狀態）預測出state value是準確的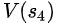，?=18

根據V(s)的定義，V(s)代表自s之后能夠獲得的平均收益，既然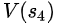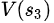=18+2=20

同理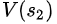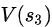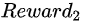，=?+=20+20=40

同理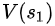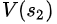，=?+==40+1=41

Temporal-Difference法

如上圖中狐貍的記事本所示，對于以上三步，狐貍既有了自己對當時state value的預測值，也有了那三個state value的“真實值”，上面的紅字就是二者的差，可以用類似“回歸”的方法最小化求解。

狐貍的反思：更新Actor

正如前文所述，critic的作用是為了準確預測Policy Gradient前的那個系數，即Likelihood Ratio。

likelihood ratio>0，應該調節actor的參數，提升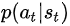的概率，即鼓勵當時采取的動作

likelihood ratio<0，應該調節actor的參數，降低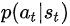抑制當時采取的動作

那么critic應該為PG貢獻一個什么樣的likelihood ratio呢？考慮以下的例子

在一個三岔路品，狐貍感受到的狀態是前路有狼、陷阱和破橋，哪條道都不好走，因此狐貍預測當前“狀態值”極差，=-100

狐貍還是硬著頭皮選擇了一條稍微好走的路，中間丟失了許多食物，收益=-20

恰好過了橋之后，一天也就結束了，最終狀態的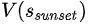=0。根據critic bootstrapping進行回推，當初過橋前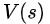“真實狀態值”=-20

那么actor中，policy gradient之前的likelihood ratio應該是多少？能不能選擇采取動作之后的直接收益，-20?如果是的話，因為選擇過橋，導致狐貍丟了20分，以后狐貍在相同狀態下（看見前路有狼、陷阱和破橋）選擇“過破橋”的概率應該降低！！！

以上結論顯然是不合適的，下次不選橋，難道要選狼與陷阱？！哪里出錯了？

換個思路：

當初在岔路口時，狐貍對當時state value的預測是-100，

選擇了破橋之后，根據critic bootstrapping推導回去，發現之前在岔路口時的狀態還不至于那么差，“真實state value”=-20。

回頭來看，選擇“破橋”還改善了當時的處境，有80分的提升。

因此，之后在相同狀態下（看見前路有狼、陷阱和破橋）選擇“破橋”的概率，不僅不應該降低，反而還要提高，以鼓勵這種明智的選擇，顯然更合情合理。

這里，某個狀態s下的state value的“真實值”與預測值之間的差異，就叫做Advantage，拿advantage作為Policy Gradient之前的乘子，整個算法就叫做Advantage-Actor-Critic (A2C)。

Advantage

注意state value的“真實值”與預測值之間的差異在Actor與Critic上發揮的不同作用

在Actor中，這個差值就叫做Advantage，用來指導Actor應該鼓勵還是抑制已經采取的動作。動作帶來的Advantage越大，驚喜越大，下次在相同狀態下選擇這個動作的概率就應該越大，即得到鼓勵。反之亦然。

在Critic中，這個差值就叫做Error，是要優化降低的目標，以使Agent對狀態值的估計越來越準確。間接使Actor選擇動作時也越來越準確。

其他

A2C的主要思路就這樣介紹完畢了。在原漫畫中，還簡單介紹了A3C、Entropy Loss的思想，就屬于旁枝末節，請各位看官們移步原漫畫。其實A3C的思路也很簡單（實現就是另一回事了），無非是讓好幾只狐貍并發地做實驗，期間它們共享經驗教訓，以加速學習。

A3C

小結

本篇算是一個半原創吧，在翻譯的同時，也增加了我對Actor-Critic的理解。

對于初學RL的同學，希望本文能夠幫你們破除RL的神秘感，理清各算法發展的脈絡，以后在David Silver課上看到那些公式時，能夠有“似曾相識”的感覺。

對于掌握了RL基本算法的同學，也希望你們能夠像我一樣，當遇到實際問題時，先想到漫畫中的小狐貍，定位問題，再去有的放矢地去翻書找公式。

很佩服原漫畫的作者，能將復雜的公式、原理用如此通俗易懂、深入淺出的方式講明白。再次向原作者致敬，Excellent Job !!!