個人簡介:一個熱愛編程的在校生,我的世界不只有coding,還有writing。目前維護訂閱號「苦逼的碼農」,專注于寫「算法與數據結構」,「Java」,「計算機網絡」。
ps:最近幾天正在刷一些有關動態規劃的題,我會把自己學習時的想法以及做題的想法記錄下來。
題目1:一只青蛙一次可以跳上1級臺階,也可以跳上2級。求該青蛙跳上一個n級的臺階總共有多少種跳法
對于這道題,我第一眼看到的想法是用遞歸的做法的,用遞歸的方法做題,我覺得最重要的就是找出 這個函數與下一個函數之間的關系 以及 一個函數體結束的臨界條件(即遞歸的結束)。
例如就本題而言,
1.第一步先找這個函數與下一個函數之間的關系:
假如有n個臺階,跳上一個n級的臺階的跳法總數為f(n).
我們在跳的過程中,每一次有兩種跳法,即跳一個或兩個臺階。
第一種跳法:第一次我跳了一個臺階,那么還剩下n-1個臺階還沒跳,剩下的n-1個臺階的跳法有f(n-1)種。
或者用
第二種跳法:第一次跳了兩個臺階,那么還剩下n-2個臺階還沒,剩下的n-2個臺階的跳法有f(n-2)種。
由此不難得出遞歸公式:f(n) = (n-1) + f(n-2);
2.第二步,找出遞歸的結束條件
當n <= 0時,跳法為0,即此時f(n) = 0
當只剩下一個臺階n = 1時,那么只有一種跳法,即f(1) = 1;
當n = 2時,此時跳法為2種,即f(2) = 2;
函數與函數之間的關系以及遞歸的臨界條件都找出來了,那么接下來就可以開始寫代碼了。如下所示:

不過觀察一下你就會發現,其實在遞歸的過程中,有很多相同的)f(n)重復算。
如下圖:
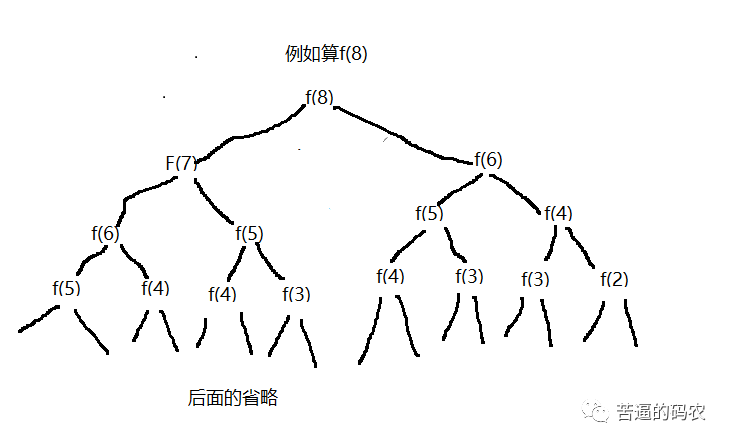
算一下你就知道,時間復雜度是指數級別的。如果是比賽這樣做的話,絕對超時不通過
因此對于那些重復算過的,其實我們可以不用在重復遞歸來算它的,也就是所我們可以把f(n)算的結果一邊給保存起來,這種就是動態規劃的思想。
也就是說,我們可以把每次計算的結果保存中一個map容器里,把n作為key,f(n)作為value.然后每次要遞歸的時候,先查看一下這個f(n)我們是否已經算過了,如果已經算過了,我們直接從map容器里取出來返回去就可以了。如下:
這種方法會快很多很多。
實際上,對于f(n) = f(n-1) + f(n - 2)這種有遞推關系的題,其實和斐波那契數列很相似,還可以這樣做:
問題2: 一只青蛙一次可以跳上1級臺階,也可以跳上2級……它也可以跳上n級。 求該青蛙跳上一個n級的臺階總共有多少種跳法。
分析,其實這道題和上面那道題一樣的,只是本來每次跳有兩種選擇,現在有n中選擇,即f(n) = f(n-1) + f(n - 2) + f(n-3)+.....+f(1);
因此做法如下:
如果你有其他想法,或者更完美的做法,歡迎指點江山。
下面為大家講解另外兩道,難度會提升一點點
數字三角形案例
題目描述 Description 下圖給出了一個數字三角形,請編寫一個程序,計算從頂至底的某處的一條路徑,使該路徑所經過的數字的總和最大。 注意:每一步可沿左斜線向下或右斜線向下
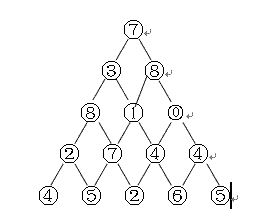
輸入描述: 第1行是輸入整數(如果該整數是0,就表示結束,不需要再處理),表示三角形行數n,然后是n行數樣例輸入: 5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5
解題思路:對于這種有多種選擇的題,一般都可以使用遞歸的方法來做,上節講過,對于遞歸的題,最重要的 就是找出遞歸的兩個條件:
1. 兩個函數之間存在的關系 2. 遞歸結束的臨界條件
我們先來聲明一些變量來記錄一些東西
1. 用D(i,j)這個二維數組來記錄這個數字三角形,i表示第i行,j表示第j列,D(i,j)表示第i行j列這個點的值 2. MaxSum(i, j) : 從D(r,j)到底邊的各條路徑中,最佳路徑的數字之和(動態規劃記錄狀態會用到) 3. state(i,j):用來記錄D(i,j)這個點是否計算過,如果還沒有計算過,則state(i,j) = -2,否則state(i,j) = MaxSum(i,j).
現在我們來尋找遞歸的兩個條件
1. 我們從第0行開始一直走,顯然,當我們走到最后一行時,遞歸結束,此時i = n-1(因為我們從第0行開始算)
2. 當我們處在D(i, j)這個點時,我們可以筆直往下走,也可以斜著往下走,有兩種走法 。我們的目標時找出使總路徑較大的點,可以得到遞歸公式:
MaxSum(i,j) = max{MaxSum(i+1, j), MaxSum(i+1, j+1)} + D(i, j)
找出了這兩個條件,就好做了。代碼如下:
int MaxSum(int i, int j){ if(i == n-1) return D[i][j];//最底層,把該點的路徑值返回 int x = MaxSum(i + 1, j);//計算筆直向下走時的最優路徑 int y = MaxSum(i + 1, j + 1);//計算斜向下走時的最優路徑 return max(x,y) + D[i][j]; }
問題所在:
和上次講的一樣,這種遞歸屬于暴力遞歸,會有很多重復計算的。和上次講的跳臺階那個類似。時間復雜度是O(2的n次方)
重復計算的次數如下圖所示

下面我們采用動態規劃的方法(遞歸動態保存)
其實,我們可以每次在計算D(i,j)的時候,把計算出來的最優解MasSum(i,j)保存起來, 下次需要的時候,先查看D(i,j)是否之前計算過,如果計算過,直接取出來就可以了。前面說過我們把值存放在state(i,j)這個數組里。
代碼如下所示
` int MaxSum(int i, int j){ if(i == num)//臨界值 return D[i][j]; else if (state[i][j] != -2)//表示這個 點已經計算過了 { return state[i][j]//直接取出返回 }else//否則的話就只好乖乖計算 { int x = MaxSum(i + 1, j); int y = MaxSum(i + 1, j + 1); state[i][j] = max(x,y) + D[i][j];//保存起來 return state[i][j]; } }`
時間復雜度為O(n2)O(n2),因為三角形的數字總和為n(n+1)/2n(n+1)/2
ps:其實這道題也可以用遞推方法的動態遞歸來接,從底部往上算起,有興趣的可以思考下。有興趣且想不出的可以問我勒
二、
學這個最重要的就是多練些題了,剛開始的時候盡量找寫簡單點的題,函數與函數之間的遞歸關系比較容易 找的題。下面找給大家介紹道題,和上次講的類型比較一樣,算是比較基礎的題:
問題: 我們可以用2*1的小矩形橫著或者豎著去覆蓋更大的矩形。請問用n個2*1的小矩形無重疊地覆蓋一個2*n的大矩形,總共有多少種方法?
還是我說的一樣,找出
(1).遞歸的結束條件。
(2).函數與函數之間的遞歸關系
1.先找結束條件:
(1)當 n < 1時,顯然不需要用2*1塊覆蓋,應該返回 0。
(2)當 n = 1時,只存在一種情況
(3)當 n = 2時,存在兩種情況
(4)當 n > 2時,顯然是需要橫著放和豎著,這時兩種情況交替放,就會產生遞歸的之間的函數關系(下圖是n=3的情況)
即 f(n) = f(n-1) + f(n-2). (有木發現這些題都很類似,解法幾乎一樣)
代碼如下所示
int f(int n){ if(n < 1)return 0 ? ?else if(n == 1)return 1 ? ?else if(n == 2)return 2 ? ?else return f(n-1) + f(n-2) }
老規矩,這樣做,有很多重復算的,采用動態記錄的方法。以n為key,f(n)為value保存在map容器中
Map
-
函數
+關注
關注
3文章
4345瀏覽量
62893 -
MAP
+關注
關注
0文章
49瀏覽量
15164 -
遞歸
+關注
關注
0文章
29瀏覽量
9048
原文標題:遞歸與動態規劃:基礎例題分析
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
基于遞歸網絡的傳感器動態建模方法
遞歸網絡模型在傳感器動態補償中的應用
基于動態對角遞歸網絡的變壓器故障診斷
動態規劃方法的利用matlab實現及其應用的有效工具詳細資料概述
看動畫輕松理解“遞歸”與“動態規劃”
經典動態規劃:戳氣球問題

動態規劃和遞歸有什么區別和聯系
算法時空復雜度分析實用指南(上)




 遞歸與動態規劃:基礎例題分析
遞歸與動態規劃:基礎例題分析











評論