引 言
信號的平穩性檢驗在隨機信號處理中起著十分基礎的作用。由于平穩信號和非平穩信號的性質差別顯著,因此在處理信號之前先行判斷它的平穩性就顯得尤為重要。雖然信號平穩性的定義十分明確,但是實際判斷過程卻是復雜的,例如觀察尺度對信號平穩性判斷就有很大的影響。
這一領域的研究已經取得了一定的成果。一些人提出了受限和帶參數的非平穩性判定方法,而另一些人則將他們的平穩性判定建立在對原始數據的一些假設上。而對于更一般信號的平穩性檢驗的研究還沒有取得太多成果。提到了這一問題,并且提出了一種新的檢驗平穩性框架。這一框架混合了時頻透視法和有名的替代數據法。它的基本思想是引入“可控噪聲”,即替代數據。并且由于替代數據的一些特性,它可以作為平穩性的*判標準。設計了一個信號平穩性檢驗系統,并在Matlab的GUI開發環境下實現了圖形用戶界面的設計。實踐表明,本系統不但提供了友好的用戶界面,并且可以方便地完成信號的平穩性檢驗。
1平穩性檢驗原理
1.1 平穩性定義及其檢驗的重要性

另一方面,如果{xl(t))是非平穩的,它的μx(t)和r(t1,t2)就是時變的或者說和時間相關的。這樣它的PSD就應該放在時頻域分析。
由此可見,平穩性檢驗是任何信號處理前必不可少的一步,它決定了后續處理可以使用何種方法。
1.2 替代數據
替代數據的概念最初是由Theiler和其合作作者提出的,這種技術是用來產生一種所謂的“替代數據”,這種替代數據是平穩的,同時保持了原數據的一些相關的統計特性。

Theiler提出了一種具體的產生替代數據的方法。由這種方法產生的替代數據是平穩的,同時保持了原數據的二階統計特性。具體地說,替代數據保持了原數據功率譜的幅度值不變。
根據Wiener-Khintchin理論,信號的功率譜等于其傅里葉變換的幅值平方。因此保持信號的功率譜幅度值不變,就是保持其傅里葉變換的幅度值不變。因此,假設原數據為x(t),它的傅里葉變換為
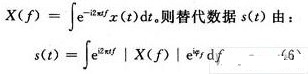
產生。其中,φf是在[-π,π]上均勻分布的隨機相位。這樣就保證了s(t)和x(t)有相同的傅里葉變換幅值。在下面的例子中也可以看到,這樣產生的s(t)也是平穩的。
1.3時頻分布
時頻分布主要用于分析非平穩隨機信號的功率譜。由于非平穩隨機信號的功率譜是時變的,因此在原來功率譜的基礎上再引入時間軸,成為時頻分布(TFD)。TFD可以顯示出信號的功率譜隨時間的變化情況。
具體來說,根據定義,信號x(t)的時頻分布Sx,K(t,f)可以表示為:
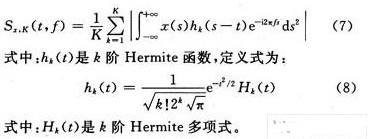
1.4 平穩性檢驗
平穩性可以體現在頻譜隨時間的波動上。具體來說,對于平穩信號,其頻譜不隨時間變化;而對于非平穩信號,其頻譜會隨時間改變。因此,可以通過比較不同時間點上頻譜的相似程度來判斷信號的平穩性。
按照文獻[4]中的檢驗方法,定義不同時間點上的頻譜與頻譜平均值的距離cn(x)為:

2用戶界面生成
2.1 Matlab中用戶界面的生成
Matlab為用戶設計圖形界面提供了一個高效、方便的集成環境。在Matlab中,基本的圖形對象主要包括坐標軸、控件、下拉菜單和內容菜單。用戶可以通過這些對象設計出界面友好,功能強大,操作簡單的圖形用戶界面。圖形用戶界面的生成主要分為以下幾個步驟:
(1)規劃所設計的圖形用戶界面,主要包括:確定需要哪些窗口,每個窗口怎樣布局,窗口中的各個對象各有什么功能,對象之間如何配合工作,以及相應的異常處理;
(2)在Matlab提示行下輸入GUIDE,載人用戶界面開發環境;
(3)利用Layout Editor,完成用戶面板以及界面的制作,并對相應的按鈕及控件屬性進行適當的設置;
(4)在Programme Editot中編輯各個對象的回調函數,實現各個對象韻具體功能;
(5)利用Mfile編譯器生成客戶端,完成隨機數據仿真系統的設計。
2.2 用戶界面介紹
本文所實現的用戶界面主要包括兩個窗口,分別是主窗口和數據生成窗口。由于Matlab對保存繪圖區域有限制,因此設計時沒有在窗口中設置固定的繪圖區域。窗口只相當于一個命令菜單,所有的繪圖將會以獨立窗口的形式根據用戶需求動態產生。這樣便于用戶對比和保存圖片。下面對主要窗口分別加以介紹。
2.2.1 主窗口介紹
主窗口如圖1所示。主窗口主要用于繪制原數據和替代數據的各種波形以及顯示平穩性檢驗結果。
其中,“Create/Open Original Data”按鈕用來打開數據生成窗口。
“View/Change Parameters”按鈕用來查看或改變當前仿真參數,它在原始數據存在的情況下才有效。主要的仿真參數有:
“Time Scale of TFD”和“Frequency Scale of TFD”用于確定繪制TFD圖片時的時間/頻率軸采樣周期,由于計算和顯示時頻分布圖比較耗費時間,將采樣周期設大,可以提高速度,但是相應的時頻分布圖的分辨率會下降。
“Max Level of Hermite Function”用于確定求TFD時所使用Hermite函數的最高階數。最高階數越高,則分辨率越高,但是相應的計算時間會加長。
“The Number of Surrogates”用于確定平穩性檢驗時所用的參考替代數據個數。個數越多,則檢驗結果越精確,但是會極大地延長計算時間。
“Create Surrogate”按鈕用于產生替代數據,其在原始數據存在的情況下才有效。由于替代數據具有隨機性,因此用戶可以多次產生不同的替代數據,觀察它們的性質。
右上方的下拉菜單用于選擇需要繪圖或者保存數據的對象,主要包括原始數據的時域、頻域和時頻域圖,替代數據的時域、頻域和時頻域圖,以及替代數據的平穩度分布。它在原始數據存在的情況下才有效。
“Show Selected Plot”按鈕用于在新窗口中繪制下拉菜單所選圖線,它在原始數據存在的情況下才有效。
“Save Selected Data”按鈕用于保存下拉菜單所選圖線對應的數據,它在原始數據存在的情況下才有效。
2.2.2 數據生成窗口
數據生成窗口如圖2所示。數據生成窗口主要用來產生實驗用數據或者打開已經存在的實驗數據。
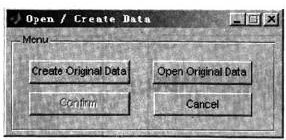
“Creat Original Data”按鈕用來產生測試用數據。按下此按鈕后會提示輸入產生數據用的參數。由于數據是通過公式:
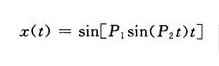
產生的調頻信號,因此需要確定參數P1和P2,另外還要確定t的區間和采樣周期。數據成功產生后會在新建窗口中顯示該數據時域波形。如果當前存在數據波形,將會覆蓋它。
“Open Original Data”按鈕用來打開已經存在的數據文件。選擇好文件后會提示輸人參數。主要包括讀人數據的時間起點、時間采樣周期和數據長度。數據成功讀入后會在新建窗口中顯示該數據時域波形。如果當前存在數據波形,將會覆蓋它。
“Confirm”按鈕用于確認新建窗口顯示的數據就是用戶想要的數據,并返回主窗口。它在創建或打開的數據存在的情況下才有效。
3數據仿真和分析
將實驗數據取為調頻信號x(t)=sin(sin(t/8)πt)。t起始為0,采樣周期為0.1 s,數據長度為400個點,其時域波形和頻域波形如圖3所示。
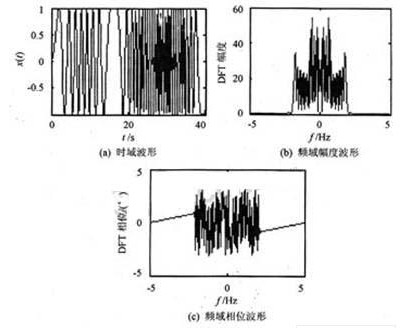
由式(6)產生的替代數據s(t)的時域波形和頻域波形如圖4所示。
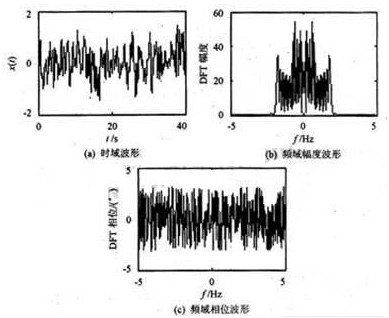
由圖3和圖4不難看出,替代數據與原數據的傅里葉變換幅值相同,但替代數據傅里葉變換的相位是隨機的。
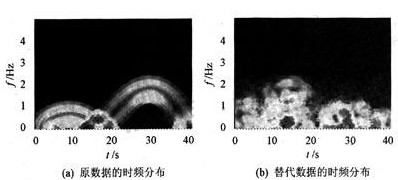
圖5顯示了由式(7)計算得到的原數據和替代數據的時頻分布圖。由圖5中可見,原數據的時頻分布圖有明顯的結構性。它表明是非平穩的,而替代數據的時頻分布圖的結構性較原數據有明顯減弱,表明替代數據的平穩性增加。
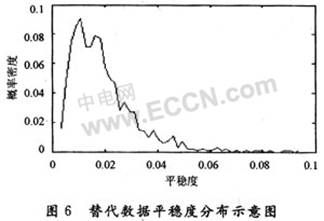
由式(11)計算得到的?0的概率密度函數f(?0)如圖6所示,其中一共計算了1 000次替代數據。
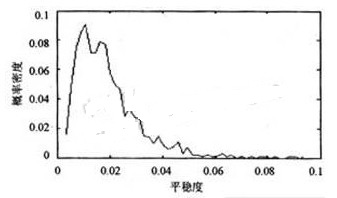
由圖6可見,替代數據的平穩度主要分布在0.02附近。數據的平穩度落在0~0.04之間可以認為是平穩的,而在此之外可以認為是非平穩的。
由式(11)計算得到的?1=0.046。位于上述區間之外,因此判為非平穩。這一結果也與圖5所示的結果相吻合。
4結 語
利用替代數據法和時頻透視法,并采用Matlab的GUI開發環境,設計了一個信號平穩性檢驗系統。該系統的用戶界面友好。利用該系統可以觀察信號及其替代數據的頻域和時頻域波形,檢驗信號的平穩性。
-
matlab
+關注
關注
185文章
2980瀏覽量
230825 -
噪聲
+關注
關注
13文章
1125瀏覽量
47495 -
GUI
+關注
關注
3文章
662瀏覽量
39827
發布評論請先 登錄
相關推薦
基于Matlab GUI怎么實現串口數據發送和接收?
基于MATLAB的GUI設計伺服驅動系統仿真軟件
基于Matlab GUI的串口通信編程實現

基于Matlab_GUI的新型界面開發方式

基于MATLAB GUI的語音信號特征提取系統設計
基于MATLAB GUI的水汽自動處理系統的設計
基于MATLAB環境下采用C8051F060實現鉆井井眼姿態監測系統的設計
EMD信號處理方法如何在LabVIEW和MATLAB中的實現




 在Matlab的GUI開發環境中實現信號平穩性檢驗系統設計
在Matlab的GUI開發環境中實現信號平穩性檢驗系統設計












評論