無線傳感器網絡(Wireless Sensor Networks)是當前在國際上備受關注的、涉及多學科高度交叉、知識高度集成的前沿熱點研究領域 .對于傳感器網絡來說, 傳感器節點的位置信息至關重要, 事件發生的位置或獲取信息的節點位置是傳感器節點監測消息中所包含的重要信息, 沒有位置信息的監測數據往往毫無意義。因受成本、功耗、擴展性等問題的限制, 為每個傳感器安裝GPS模塊等這些傳統定位手段并不實際, 甚至在某些場合可能根本無法實現, 而且GPS定位在定位精度、實時性方面有時并不能滿足特定的需求, 因此針對具體的定位需求, 必須采用一定的算法機制來實現傳感器節點的定位。
無線傳感器網絡節點按定位過程中是否需要測距信息, 可分為無需測距的定位方法和基于測距技術的定位方法。近年來, 關于傳感器網絡節點定位技術研究成為無線傳感網絡技術的一重要研究熱點并取得大量的研究成果。其中, 具有代表性算法研究成果有: 凸規劃算法及其改進算法 , APS 算法、Cooperative Ranging 、AHLos 算法、nHopMultilateration Primitive 算法、MDS-MAP 算法等。
無需測距的定位方法被認為是一類具有好的成本效益的解決方案。在無需測距定位方法中, DV-Hop( Distance Vector-Hop) 節點定位方法由于對信標節點比例要求較少, 定位精度較高, 目前已成為一種經典的無需測距定位方法。
DV-Hop定位方法的主要思想是引入最短路徑算法到信標節點的選擇過程中, 從而在未知節點的位置估計過程中可以有效利用多跳信標節點的位置信息, 這種方法可以大大減少實現網絡定位所需信標節點的比例(密度), 從而大大降低網絡的布置成本。
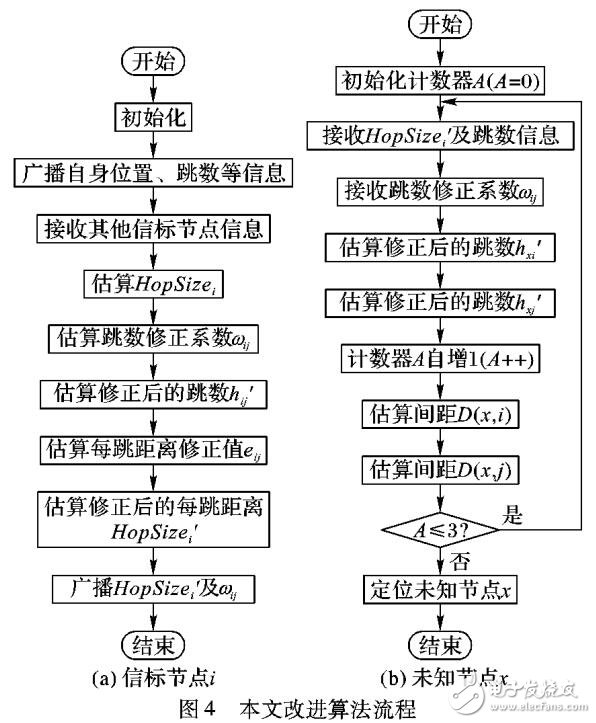
本文就DV-Hop算法的誤差成因進行了分析,在DV-Hop 定位算法優點的基礎上, 針對該算法只適用于各向同性網絡的不足, 對DV Hop 算法進行局部優化, 使得改進后的DV-Hop 算法減少了數據包發送量, 提高了定位精度, 并且對于不規則形狀的節點分布具有較強的適應性。
1 DV-Hop 定位算法
DV-Hop定位算法是APS算法系列中使用最為廣泛的定位方法, 其定位過程不依賴于測距方法, 利用多跳信標節點信息來參與節點定位, 定位覆蓋率較大。DV-Hop 算法非常類似于傳統網絡中的距離向量路由機制, 在該定位機制中, 未知節點首先計算與信標節點的最小跳數, 然后估算平均每跳距離, 利用最小跳數乘以平均每跳距離, 估算得到未知節點與信標節點之間的距離, 再利用三邊測量法或極大似然估計法計算未知節點的坐標。
DV-Hop定位算法可以分為以下3個階段:
( 1) 計算未知節點與每個信標節點的最小跳數。
信標節點向鄰居節點廣播自身位置信息的分組, 其中包括跳數字段, 初始化為0.接收節點記錄具有到每個信標節點的最小跳數, 忽略來自同一個信標節點的較大跳數的分組。然后將跳數值加1,并轉發給鄰居節點。通過這個方法網絡中的所有節點能夠記錄下到每個信標節點的最小跳數。
( 2) 計算未知節點與信標節點的實際跳段距離。
每個信標節點根據第1階段中記錄的其他信標節點的位置信息和相距跳數, 利用式(1)估算平均每跳的實際距離:
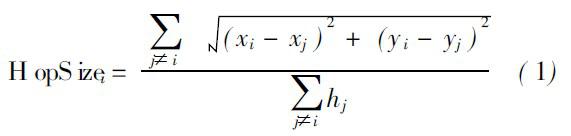
其中, ( xi, yi )、( xj, yj )是信標節點i、j 的坐標, hj 是信標節點i與j( i≠j)之間的跳段數。
然后, 信標節點將計算的每跳平均距離用帶有生存期的字段的分組廣播到網絡中, 未知節點僅記錄接收到的第1個每跳平均距離, 并轉發給鄰居節點。這個策略可以確保絕大多數未知節點從最近的信標節點接收每跳平均距離。未知節點接收到平均每跳距離后, 根據記錄的跳數, 計算到每個信標節點之間的距離。
( 3) 未知節點計算自身位置。
未知節點利用第2階段中記錄的到各個信標節點的跳段距離, 利用三邊測量法或極大似然估計法計算出自身坐標。
如圖1所示, 經過第1和第2階段, 能夠計算出信標節點L1 與L2、L3 之間的距離和跳數。信標節點L2 計算得到校正值(即每跳平均距離)為( 40 +75) / ( 2+ 5) = 16. 42.假設未知節點A 從L2 獲得校正值, 則它與3 個信標節點之間的距離分別為L1: 3×16. 42, L2: 2×16. 42, L3: 3×16. 42, 最后可利用三邊測量法確定節點A 的位置。
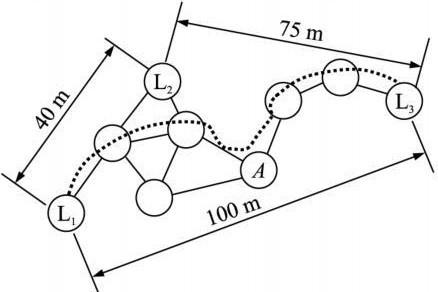
圖1 DV H op算法示意圖
DV-Hop算法采用平均每跳距離來估算實際距離, 對節點的硬件要求低, 實現簡單。其缺點是利用跳段距離代替直線距離, 存在一定的誤差。
2 DV-Hop算法誤差分析
在DV-Hop定位算法中, 算法的第1階段, 由于傳感器節點隨機分布和廣播分組過程中可能存在沖突等因素, 節點得到的到信標節點的最小跳數存在有一定偏差, 且跳數越多, 偏差越大。
在信標節點采用式(1)估算平均每跳距離時,所利用的是除本節點外所有其他信標節點, 所以得到的是全網絡范圍內的平均每跳距離, 不能反映本信標節點局部范圍內的網絡密度分布情況。因此,采用該方法得出的平均每跳距離在密度均勻的各向同性網絡中影響不大, 但在密度不均勻的各向異性網絡中, 就會造成較大的誤差。
在DV-Hop算法的第3階段, 未知節點利用了到所有信標節點的距離信息, 而據前面的分析, 未知節點到信標節點的最小跳數可能有偏差, 跳數越多,偏差越大, 且第2階段得出的平均每跳距離也只是對實際距離的一種估算, 不可避免會存在著誤差, 這樣信標節點距未知節點跳數越多, 二者之間的跳段距離估算誤差就越大, 利用較遠信標節點的距離信息參與位置計算, 反而可能降低了定位結果的精確度。
3 DV-Hop算法改進
根據上面的分析, 本文對DV-Hop算法加以改進, 改進后的方法計算過程仍與原DV-Hop算法大致相同, 下面僅對改進之處加以說明。
在DV-Hop算法的第1階段, 信標節點向鄰居節點廣播自身位置信息的分組時, 該分組加上生存期字段n, 其它節點在轉發該廣播包時, 首先檢測生存期字段, 如果n 大于1, 則n = n - 1, 轉發廣播包;如果n 不大于1, 則不再轉發該廣播包, 以保證該分組僅在n跳范圍內廣播。這樣每個節點僅收到n跳范圍內信標節點信息, 降低了原DV-Hop算法全網洪泛造成的高通信開銷、高分組沖突概率。
在DV-Hop算法的第2階段, 利用式(1)估算平均每跳實際距離時, 信標節點j 取自該節點n 跳范圍內跳數最少的m 個信標節點。這樣處理保證估算的平均每跳實際距離更符合該節點附近的節點分布, 提高了距離估計精確度, 并使該方法適用于各向異性網絡。
最后, 在未知節點利用極大似然估計法計算自身坐標時, 由于信標距離該未知節點跳段越近, 二者之間的距離估計越精確(概率意義上), 所以這里只取跳段距離最近的l個節點進行極大似然估計法運算。這樣, 既提高了定位精確度, 又降低了節點的計算開銷。
參數n、m、l的取值要綜合考慮信標節點比例、網絡的連通度、傳感器節點分布等因素。一般情況下, n 要保證絕大部分未知一個節點能收到3 個以上的信標節點分組, 而m、l取4~ 6即可取得相對高的精確度。
4 仿真分析
為了評估所提出的改進算法的可用性和有效性, 作者利用Matlab7. 0對DV-Hop算法及本文提出的改進算法( Improved DV- Hop, IDV H op)進行了實驗仿真, 并對相關實驗結果進行分析。
仿真分析的網絡模型的標準參數如下: 設定節點射頻通信距離是10個長度單位, 網絡規模為400個節點, 均勻隨機分布在邊長為100 個長度單位的正方形中(這時的平均連通度為11左右), 其中信標節點比例為5% .在相同的網絡場景下, 通過改變總節點數來改變網絡的連通度, 從而實現相同網絡場景下不同網絡連通度的仿真實驗條件。為消除隨機性產生的誤差, 所得仿真結果均為同樣參數下仿真100次所得結果的平均值。
( 1) 可定位節點比例。
可定位節點比例(也稱算法覆蓋率) 是指通過定位算法成功實現位置估計的未知節點數量占網絡中所有未知節點數量的百分比。通過仿真結果(圖2, IDV- Hop算法中n 取值為3)。
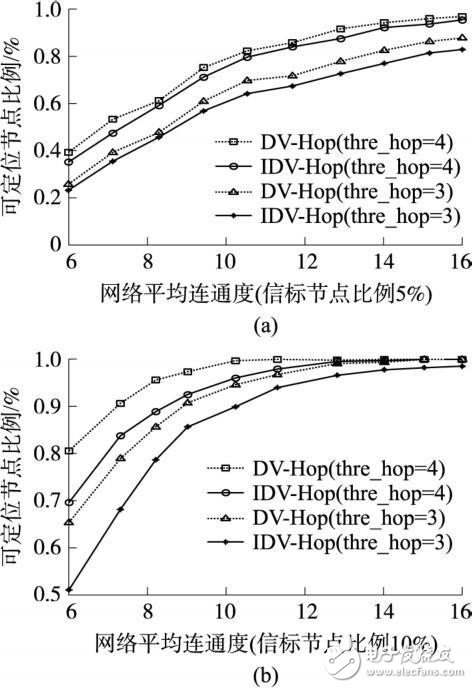
圖2 可定位節點比例
可以看出, 兩種算法的可定位節點比例均和網絡的平均連通度、信標節點比例、算法中分組廣播的生存期字段的取值都有關系; 在同樣的參數條件下,IDV-Hop算法的可定位節點比例和DV-Hop算法相比要低若干個百分點, 這是因為在算法第1階段, 可控洪泛使得部分未知節點收到的信標節點小于3而不能實施第3階段的定位運算。
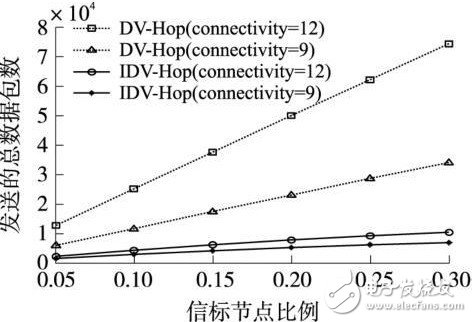
圖3 數據包發送量
(2) 數據包發送量。
圖3為網絡連通度為9和12時時, DV-Hop算法與IDV-Hop算法在數據包發送量上的比較, 其中橫坐標表示信標節點所占的比例, 分組廣播的生存期字段均取3, IDV-Hop算法中的n 取值為3.從圖中可以看出, 網絡的數據通信量隨信標節點比例和網絡連通度的增加而增加。而在同樣的網絡參數下, IDV-Hop 算法的數據通信量遠小于DV-Hop算法(不到原通信量的20% ) , 這主要是由于在算法的第1階段, IDV-Hop采用的部分洪泛代替了DV-Hop算法全網范圍洪泛的緣故。
另外, IDV-Hop算法的數據通信量與還與n的選擇有關, 當n較小時, 該算法限制洪泛跳數范圍內小,所需的數據通信量就小, 但n 值也不是越小越好, 如前面分析, 較小的n 值會降低算法的可定位節點比例。
( 3) 定位精度。
定位誤差( Localization E rror, LE)指的是通過定位算法得到的未知節點的估算位置與實際位置的偏差, 這種偏差可以用兩者之間的歐氏距離除以節點的通信半徑來衡量, 如式( 2)所示。顯然, 定位誤差的大小能最直接說明算法的有效性。
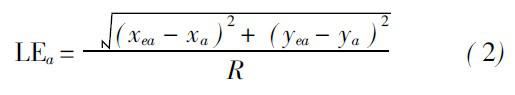
其中(x ea, yea )為未知節點的估算位置, ( xa, ya )為未知節點的實際位置, R為節點的通信半徑。
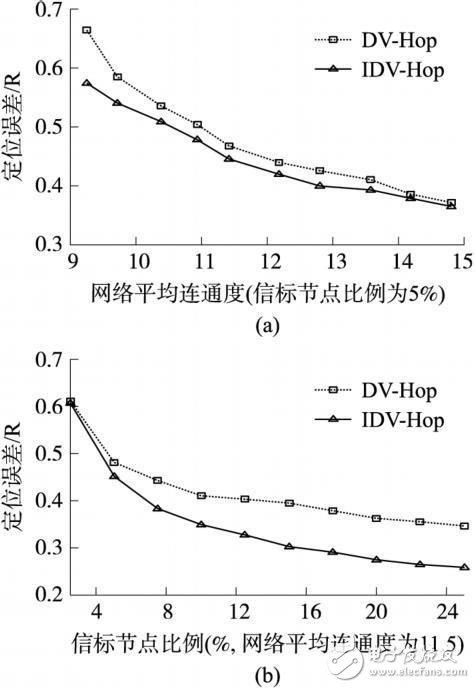
圖4 節點均勻分布時的定位精度
圖4給出了傳感器節點均勻分布時, DV-Hop算法和IDV-Hop算法定位精度比較結果。可以看出,在各向同性網絡中, 在相同的網絡連通度和信標節點比例下, 改進后的算法比原算法定位精度均有所提高, 特別是在大于6% 時, IDV-Hop算法的定位精度隨著信標節點比例升高而迅速提高, 而原DVHop算法提高并不明顯, 這是由于信標節點比例越高, IDV-Hop算法越有機會采用距離估計精確度較高的鄰近信標節點進行定位運算, 從而提高了定位精度, 驗證前面對DV-Hop算法的分析。
圖5為傳感器節點非均勻分布時(節點分布從左到右逐漸由疏變密),DV-Hop算法和IDV-Hop算法定位精度結果。與圖4相比, DV-Hop算法定位精度大幅下降, 而IDV-Hop算法僅稍有下降。在同樣的網絡參數下, IDV-Hop算法的定位精度比DV H op算法提高了大約20%, 可見, 改進后的算法更適用于各向異性網絡。
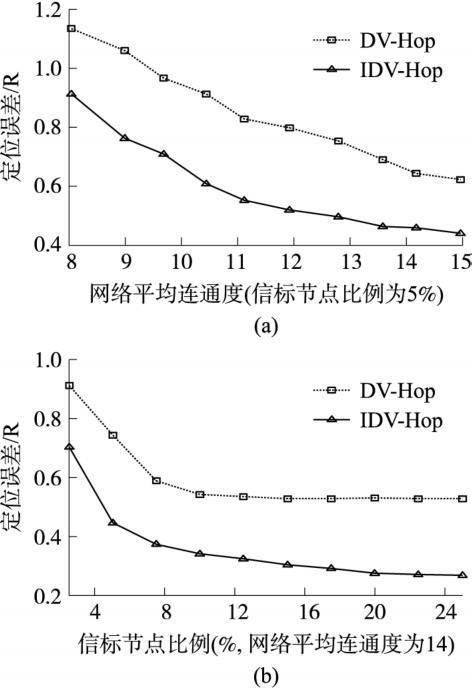
圖5 節點不均勻分布時的定位精度
5 結語
本文分析了DV-Hop算法只適用于各向同性網絡的原因, 對DV-Hop算法進行局部性優化, 給出了無線傳感器網絡無需測距DV-Hop 定位的改進算法。仿真結果表明, 改進后的算法可定位節點比例略有下降, 但提高了定位精度, 特別是節點非均勻分布時的定位精度, 減少了數據包發送量, 因此更適用于在實際項目中應用。
-
傳感器
+關注
關注
2552文章
51382瀏覽量
755805 -
gps
+關注
關注
22文章
2901瀏覽量
166531 -
無線傳感器
+關注
關注
15文章
770瀏覽量
98458
發布評論請先 登錄
相關推薦
基于最優跳距和改進粒子群的DV-Hop定位算法




 適用于節點不規則的異性無線傳感器網絡分布的DV-Hop定位的改進算法
適用于節點不規則的異性無線傳感器網絡分布的DV-Hop定位的改進算法











評論