1. 前言

數控系統的NURBS曲線插補技術是基于PC開放式數控系統的發展關鍵技術之一。數控加工時經常遇到諸如飛機的機翼、汽車流線型覆蓋件、成型模具型腔、汽輪機葉片等許多具有復雜外形型面的零件，CAD/CAM通常用列表曲線來描述它們。列表曲線的擬合方法很多，如三次樣條、B樣條、圓弧樣條及牛頓插值方法等。由于NURBS曲線具有良好的直觀性，且在“局部性”及收斂、逼近性方面占有優勢，已經成為當前最為通用的列表曲線擬合方法，利用NURBS在CAD/CAM系統中可以使所有的曲線具有統一的數學表達式，國際標準化組織(ISO)在其正式頒布的工業產品幾何定義STEP標準中，亦將NURBS作為產品交換的國際標準。于是，對CNC添加NURBS曲線曲面插補功能，成為現代開放式數控系統的關鍵技術之一。基于PC開放式數控系統可以充分利用PC的強大計算能力，實現NURBS曲線曲面高速度高精度的實時插補。

2．數控插補原理

在CNC系統中，插補器的硬件功能全部或部分地由計算機的系統程序來實現。CNC根據來自數據處理結果緩沖區中存儲的零件程序數據段的信息，以數字方式進行計算，不斷向系統提供坐標軸的位置命令，這種計算叫做插補計算，簡稱插補。插補軟件的任務是完成在輪廓起點到終點的中間點的坐標計算。尤其對于輪廓控制系統而言，插補是最重要的計算任務。插補必須是實時的，即必須在有限的時間內完成計算任務，對各坐標軸分配速度或位置信息。插補程序的運行時間和計算精度影響著整個CNC系統的性能指標。總結目前普遍應用的插補算法可分為兩類：

(1)脈沖增量插補。脈沖增量插補也稱為行程標量插補，就是用軟件模擬NC系統常用的逐點比較法、DDA積分法以及這兩種算法的改型算法。插補的結果是產生單個的行程增量，以一個個脈沖的方式輸出給步進電機。脈沖增量插補輸出的頻率主要受插補程序所用的時間限制，適用于中等精度和中等速度，以步進電機為驅動元件。

(2)數據采樣插補。數據采樣插補也稱為時間分割插補，適用于閉環和半閉環以直流或交流電機為執行機構的位置采樣控制系統。插補程序的調用周期可以和系統的位置采樣周期相同，也可以是采樣周期的整數倍。在這種系統中，插補程序的運行時間不多于計算機時間負荷的30%-40%，在其余時間內，計算機可以實現顯示、譯碼、刀補等數控功能。本文所研究的NURBS曲線插補算法就屬于這一類插補算法。

3. 參數曲線直接插補算法基礎

曲線表示主要有兩種方法:隱式方程法和參數方程法。參數方程法因其易于編程和計算成為CAD系統首選的曲線表示方法。一個三維曲線就可以用如下的參數方程表示:

x = x(u), y = y(u), z = z(u)

其中抽象參數u滿足0 < u <1。曲線的參數方程可以非常方便的控制多軸機床的運動，而且對各軸的控制可以是分別、獨立的進行，故數控系統的各種曲線直接插補算法都基于曲線的參數方程。通常把這三個方程合寫成p(u) = [x(u), y(u), z(u)]，或者笛卡兒分量表示形式P(u) = x(u)i + y(u) j + z(u)k ，其中i, j, k 分別為沿x, y, z軸正向的三個單位矢量。常簡記Pi = p(ui)。

插補計算就是在CNC系統的第i-1工作周期中，實時計算出滿足指定加工要求的下一個工作周期的各軸運動分量ΔPi 。例如滿足加工步長要求ΔLi的插補點Pi + 1為:

3.1 B樣條曲線的定義

非均勻有理B樣條曲線NURBS方法提出的首要理由是，為了找到與描述自由型曲線的B樣條方法相統一的、且又能精確表示二次曲線弧與二次的數學方法。因此在了解NURBS曲線之前，有必要首先了解B樣條曲線，B樣條曲線是采用控制頂點來定義曲線的，其曲線方程可寫為:

Ni, k(u),i = 0,1,K , n稱為k次規范B樣條基函數，其中的每一個k次規范B樣條基函數簡稱為B樣條。它是由一個稱為節點矢量的非遞減的參數u的序列U: u0 ≤ u1 ≤K ≤ ui + k + 1 所決定的k次分段多項式.

B樣條基Ni, k(u)通常采用截尾幕函數的差商定義，德布爾一考克斯的遞推定義為:

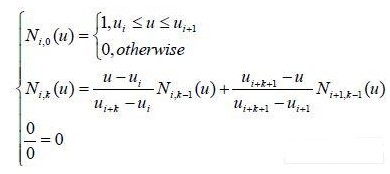
Ni, k(u)的雙下標中第二下標k表示次數，第一下標i表示序號。該遞歸公式表明，欲確定第i個k次B樣條Ni, k(u)，需要用到ui,ui + 1,K ui + k + 1共k+2個節點，包含的區間[ui,ui + k + 1]被稱為Ni, k(u)的支承區間。Ni, k(u)的第一下標等于其支承區間左端節點的下標，即表示該B樣條在參數u軸上的位置。曲線方程(23)中相應的n +1個控制頂點di,i = 0,1K n，要用到n +1個k次B樣條基函數Ni, k(u),i = 0,1,K , n。它們的支承區間的并集，被定義為這一組B樣條基的節點矢量U = [u0,u1,K un + k + 1]。

3.2 NURBS曲線的定義

在B樣條曲線定義的基礎上，若節點序列為非均勻分布，且在每個控制點處加一個表示對曲線形狀影響大小的加權因子Wi，則k階B樣條曲線相應的變為k階NURBS曲線，其公式相應為:

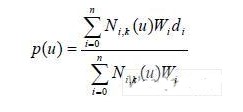
對于非周期NURBS曲線，往往取u0 = u1 =K = uk = 0,un + 1 = un + 2 =K = un + k + 1 =1,即將兩端節點的重復度取為k+1，從而使曲線兩端能相切通過控制多邊形的首、末端節點。于是，曲線定義域u∈[uk,un + 1] = [0,1]，節點矢量U = [0,0,K 0,uk + 1,K ,un,1,1,K 1]。而且由于NURBS曲線方程的有理性，使得尋求NURBS曲線的迭代公式變得相當困難。

4．NURBS曲線插補技術

4.1 傳統的CNC機床的加工方法

圖1描述了CNC機床傳統的曲線加工方法。首先，用CAD系統軟件設計加工零件的幾何模型，然后由CAM系統將刀具接觸軌跡轉化為刀具位置軌跡。以為目前的CNC系統一般只具有直線和圓弧插補功能，為了確保CNC系統能控制機床沿著刀具位置軌跡來執行加工任務，刀具位置軌跡通常被分解為一系列直線段或圓弧段（也稱為NC代碼）。應用足夠數量的直線段或圓弧段，就可以在指定的精度內逼近給定的曲線。但這種方法存在以下缺點：

1） 由于用直線逼近曲線本身是用直線代替曲線，逼近后的線是一階的，導矢不連續的，所以加工表面不光滑。

2） 在曲線的加工過程中，如果在直線部分不進行加減速，那么就要求在較低的速度下進行加工，這樣一來不能滿足高速加工的要求。并且由于直線段的一階不連續，在加工過程中會造成機床的過沖，不能保證加工的質量和精度要求。如果在曲線的加工過程中，對直線段部分的每一段直線進行加減速，會造成加工速度的不平衡，加工的質量差，時間長。

3） 大量的直線段或圓弧段將會增加加工速度的變化和曲線的加工時間，這樣將會降低曲線的平均加工速率，降低加工效率。

4） 具有復雜曲面形狀的零件的加工，需要存儲的程序段數非常龐大，而CNC系統的內存容量相對較小，因此需要分段存儲和調用，這不僅會降低系統的可靠性，也會降低加工效率。

通過設定曲線加工時的允許誤差和曲線曲率或者待加工曲線的長度，就可以確定加工任務中的最小直線段數。如果刀具實際走過的直線或圓弧段數太少，將會引起實際加工的曲線的一階和二階導矢的不連續。進而導致加工后的工件表面的光滑性和曲面的光潔度的畸變。基于以上分析，如果采用傳統的直線和圓弧的插補器，很難獲得高速，高精度的曲線加工。所以，開發一種新型的CNC插補器是十分必要的。

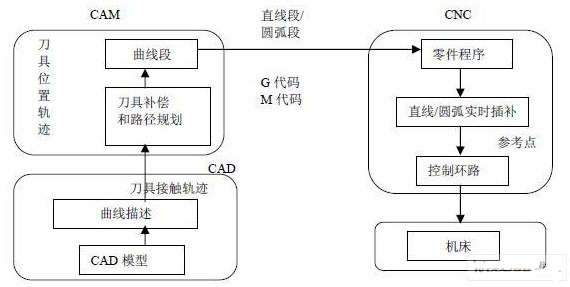
圖1 CNC機床傳統的曲線加工方法

4.2 采用NURBS插補技術的CNC機床的加工方法

圖2描述了一種新型的CNC機床的曲線曲面加工方法。在這種加工模式下，數控機床在它的伺服控制環中配備了NURBS曲線的實時插補器。因為NURBS曲線的定義參數較少，并且即可以表示解析曲線，又可以表示自由曲線，所以可以節省大量的花費在CAD/CAM和CNC機床之間的數據傳遞時間。

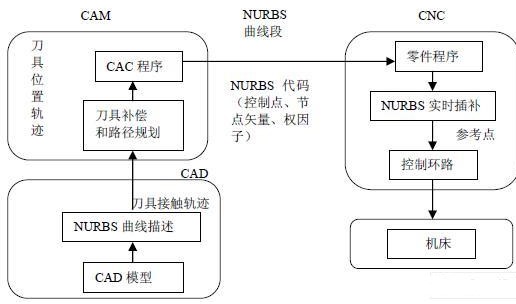
圖2 采用NURBS插補技術的CNC機床曲線曲面加工方法

一個三軸聯動的數控機床的伺服控制結構圖如圖3，其中CNC運動控制器的主要任務可以分為三部分。第一部分就是解釋從CAD/CAM系統中獲得的加工代碼。第二部分是將從第一部分中獲得的數據在一個采樣周期中轉變為CNC的伺服控制命令。第三部分就是在CNC控制器的各個運動軸上執行伺服控制命令。因為運動控制必須實時地進行，所以這三部分任務必須在一個給定的采樣周期內完成。因為代碼解釋通常都是在數控加工開始之前就完成了，所以第一部分任務不必實時完成。而且采用NURBS的加工方法只占用少量的程序內存，花費在曲線解釋上的時間可以大大的減少，因而總的加工時間也得以減少。因此在圖3中只有第二部分和第三部分需要實時進行。隨著伺服控制技術的發展，第三部分已經能夠實時的實現，所以，為了能夠成功地實現數控加工的實時運動控制，第二部分的命令生成任務必須在一個采樣周期內完成。

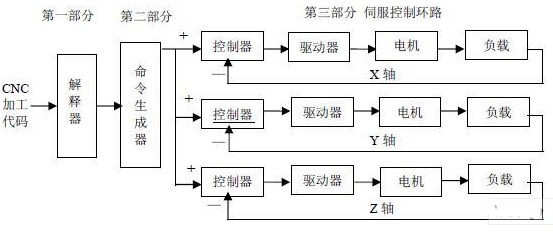
圖3 三軸聯動數控機床的伺服控制結構圖

5．結語

在現代開放式數控系統中，引入NURBS曲線進行插補，能有效地提高實時插補的速度和精度，從而進一步提高數控系統的工作效率。