編者按：Microsoft Semantic Machines資深研究科學家、UC Berkeley計算機科學博士Jacob Andreas指出，神經網絡不應視為模型，因為神經網絡的模型和推理過程不可分割。應該將推理過程視為機器學習問題的一等公民。

在大多數介紹人工智能的材料中，模型和推理過程的區分很關鍵。例如，HMM（隱馬爾可夫模型）是一類模型；維特比算法則是用于推理過程的一種算法，前向傳播算法是另一種推理算法，粒子濾波又是一種推理算法。

很多人將神經網絡描述為一類模型（他們大概也把神經網絡視作模型）。我主張這種觀點很有誤導性，將神經網絡看成糾纏不清的模型-推理對（model-inference pairs）會更有用。“模型-推理對”是一個長而拗口的詞，看起來現在也沒有什么很好的現成的簡稱，因此我將用模推（monferences）來指代這一概念。我主張我們應該將神經網絡視為模推的一個例子。（搭配某種特定的HMM參數的維特比算法的一種實現，同樣是模推。）

我將引用一些現有的論文，這些論文自然而然地符合將神經網絡視為模推這一視角——看起來這一想法對許多人來說已經是顯然的了。但我認為這一想法未曾被命名，也未曾經過系統的處理。我希望其他人會像我一樣，覺得下面的內容是有用的（或者至少厘清了一些東西）。

將神經網絡視作模型的后果是什么？讓我舉一個自己的例子來說明：

我第一次看到循環神經網絡的時候，我覺得“這是一個有趣的模型，搭配一個糟糕的推理過程”。循環網絡看起來像HMM。HMM有離散的隱藏狀態，而循環網絡有隱藏狀態向量。在HMM中進行推理時，我們保持和輸出分布相一致的隱藏狀態，但在循環網絡中進行推理時，我們僅僅保持單個向量——單個假設，加上貪婪推理過程。如果采用某種建模不確定性的方法，不是更好嗎？為什么不像卡爾曼濾波一樣對待RNN推理？

這完全錯了。探索為什么這是錯的，正是本文剩下部分的目標。

簡單來說，將循環網絡的隱藏狀態視作單個假設是毫無理由的。畢竟，一個足夠大的隱藏向量可以輕而易舉地表示前向傳播算法中的整張概率表——甚至可以表示粒子濾波的狀態。“HMM隱藏狀態 = RNN隱藏狀態”這一類比不好；“HMM解碼器狀態 = RNN隱藏狀態”這一類比更好。

讓我們通過實驗來探索這一點。（本節中的完整代碼見git.io/fN91L）。

我隨機生成了一個HMM，從中取樣了一組序列，并應用經典的最小化風險過程。最終得到的“在線標簽”精確度為62.8。

針對這一在線標簽問題，另一種完全可以接受（但某種程度上更費力）的生成模推的方法是從HMM中抽取更多樣本，然后使用(觀測, 隱藏)序列作為RNN網絡的訓練數據(x, y)：

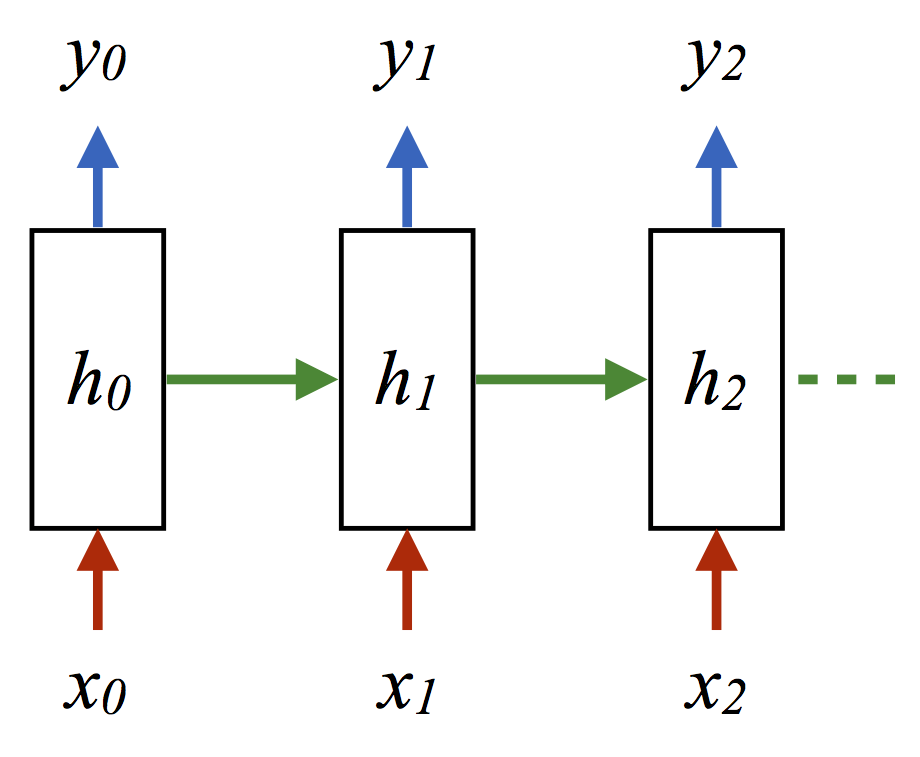
（其中每個箭頭表示內積加ReLU激活或log損失）。這一情形下取得的精確度為62.8。

兩個精確度是一樣的，這僅僅是個巧合？讓我們查看一些預測：

所以，甚至當兩個模推犯錯的時候，都犯了一樣的錯。

當然，我們知道，就這一問題而言，如果我們應用完整的前向-后向算法，并且同樣做出最大化邊際概率的預測，能得到稍好的結果。改進的經典過程得到的精確度為63.3。如我們所料，這比上面兩種在線模型的表現要好。另一方面，在取自HMM的樣本上訓練一個雙向循環網絡同樣得到63.3的精確度。

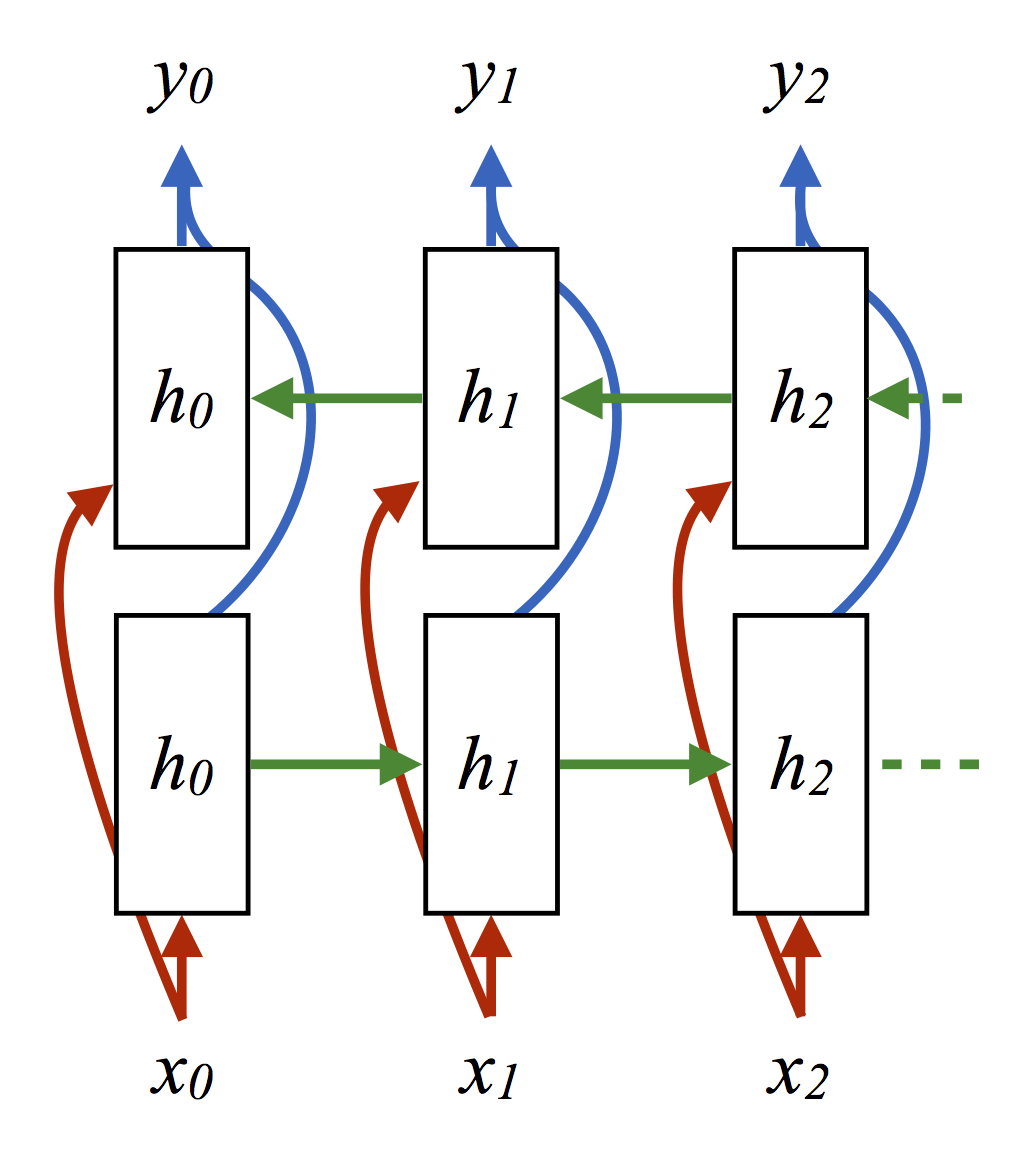
預測取樣：

注意，我們這里使用的神經網絡沒有編碼任何關于經典消息傳遞的規則，并且絕對沒有編碼任何HMM內部的生成過程。然而在兩種情形下，神經網絡都成功取得了和結構相同的經典消息傳遞過程一樣好（但沒有更好）的精確度。實際上，該神經訓練過程相當于一段代碼，這段代碼和前向-后向算法做出一致的預測，卻對前向-后向算法毫無所知！

神經網絡不是魔法——當我們的數據實際上是由HMM生成的時候，我們無法指望神經模推擊敗（信息論上最優的）經典模推。但經驗告訴我們，兩者的表現一樣好。隨著我們增強神經架構，以匹配更強大的經典推理過程的算法結構，它們的表現提升了。雙向循環網絡優于前向循環網絡；每個“真”隱藏向量間具有多層的雙向網絡（arXiv:1602.08210）可能在一些任務上表現更好。

更妙的是，我們也許可以少操心更困難的情形，也就是原本需要手工調整某種逼近推理方案的情形。（例如：假設我們的轉移矩陣是一個巨大的排列組合。在經典推理中，重復相乘可能非常昂貴，而嘗試取得轉移矩陣的低秩逼近則會損失信息。而一個神經模推卻具備緊湊地表達模型動力學的潛力。）

目前為止我們討論的是序列，但在更多結構化數據上同樣存在對應。就樹形問題而言，我們可以應用某種類似固定樹上的內向算法（aclweb/P13-1045），或者整個稀疏化解析表上的內向-外向算法（aclweb/D15-1137）。而對任意圖而言，我們可以應用“圖卷積”（arXiv:1509.09292），隨著圖卷積的重復，它開始看起來像是置信傳播。

這里有一條一般原則：任何保持離散狀態分布的推理算法，都可以轉換：

將表單元或離散分布替換為向量

將單元間的信息替換為循環網絡

展開“推理”過程（選擇一個合適的迭代數）

通過反向傳播進行訓練

所得的模推至少和相應的經典過程具備同樣的表達能力。在有必要逼近的地方，我們可以（至少從經驗上說）通過在數據上端到端地訓練，學習正確的逼近。

這種通過反向傳播逼近推理過程，但并不嘗試學習推理函數本身的想法已經提出了有一段時間了。（doi/10.1.1.207.9392、 arXiv:1508.02375）

我認為結合這一框架的各部分至少可以寫一篇句法分析的論文，而圖結構數據方面還有很多工作可以做。

我說明了模推這一角度是有用的。但是果真如此嗎？神經網絡確實是模推，而不是模型，這有準確的意義嗎？

不。這里有一個基礎性的可識別問題——我們無法真正區分“酷炫的模型搭配微不足道的推理”和“神秘的模型搭配復雜的推理”。因此，給定訓練好的神經網絡，詢問它進行推理的模型是哪個同樣毫無意義。另一方面，通過蒸餾法訓練的神經網絡（arXiv:1503.02531）看起來倒挺像“同一模型，不同模推”的良好人選。同時，將神經網絡視作模型這一角度也不應該完全忽略：它形成了成果累累的系列工作，將CRF中的對數線性回歸模型替換為神經網絡（arXiv:1507.03641）。盡管這些方法通常的賣點之一是“你可以保留動態程序”，我們之前論證了這一點在恰當組織的神經網絡上同樣成立。

不管怎么說，由于機器學習社區這一角落的研究重點在向計劃、推理和困難算法問題（nips2015/4G4h）轉變，我認為將神經網絡視作模推的角度將占統治地位。

除此以外，當我們回顧十年前的“深度學習革命”時，我認為最重要的經驗教訓是端到端訓練解碼器的重要性和推理過程，甚至在幾乎看起來完全不像是神經網絡的系統（arXiv:1601.01705）中也是如此。所以在創建學習系統的時候，不要問：“我的變量的概率關系是什么？”而問：“我如何逼近我的問題的推理函數？”，并嘗試直接學習這一逼近。為了高效地達成這一點，我們可以使用我們所知道的關于經典推理過程的一切知識。不過，我們同時也應該開始將推理視作學習問題的一等公民。

感謝Matt Gormley（他的EMNLP演講讓我開始思考這一問題），以及Robert Nishihara和Greg Durrett的反饋。

同樣感謝Jason Eisner的金玉良言：“一個拙劣的混成詞，因為monference應該是一個像model一樣的可數名詞，但它的后綴卻取自inference這個集合名詞。我可沒說infedel要好太多……”