DeepMind最新提出“神經(jīng)算術(shù)邏輯單元”，旨在解決神經(jīng)網(wǎng)絡(luò)數(shù)值模擬能力不足的問題。與傳統(tǒng)架構(gòu)相比，NALU在訓(xùn)練期間的數(shù)值范圍內(nèi)和范圍外都得到了更好的泛化。論文引起大量關(guān)注，本文附上大神的Keras實(shí)現(xiàn)。

在昆蟲、哺乳動(dòng)物和人類等許多物種的行為中，表示和操縱數(shù)值的能力都是顯而易見的。這表明基本的定量推理是智能（intelligence）的一個(gè)基本組成部分。

雖然神經(jīng)網(wǎng)絡(luò)能夠在給出適當(dāng)?shù)膶W(xué)習(xí)信號(hào)的情況下成功地表示和操縱數(shù)值量，但它們學(xué)習(xí)的行為通常不會(huì)表現(xiàn)出系統(tǒng)的泛化。具體來說，當(dāng)在測(cè)試時(shí)遇到訓(xùn)練時(shí)使用的數(shù)值范圍之外的數(shù)值時(shí)，即使目標(biāo)函數(shù)很簡單（例如目標(biāo)函數(shù)僅取決于聚合計(jì)數(shù)或線性外推），也經(jīng)常會(huì)出現(xiàn)失敗。

這種失敗表明，神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)行為的特點(diǎn)是記憶，而不是系統(tǒng)的抽象。觸發(fā)外推失敗的輸入分布變化是否具有實(shí)際意義，取決于訓(xùn)練過的模型將在何處運(yùn)行。然而，有相當(dāng)多的證據(jù)表明，像蜜蜂這樣簡單的動(dòng)物都能夠表現(xiàn)出系統(tǒng)的數(shù)值外推（numerical extrapolation）能力，這表明基于數(shù)值的系統(tǒng)化推理具有生態(tài)學(xué)上的優(yōu)勢(shì)。

DeepMind、牛津大學(xué)和倫敦大學(xué)學(xué)院的多名研究人員最新發(fā)表的論文“Neural Arithmetic Logic Units”，旨在解決這個(gè)問題。研究人員開發(fā)了一種新的模塊，可以與標(biāo)準(zhǔn)的神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)（如LSTM或convnet）結(jié)合使用，但偏向于學(xué)習(xí)系統(tǒng)的數(shù)值計(jì)算。他們的策略是將數(shù)值表示為沒有非線性的單個(gè)神經(jīng)元。對(duì)于這些single-value的神經(jīng)元，研究人員應(yīng)用能夠表示簡單函數(shù)的運(yùn)算符（例如 +， - ，×等）。這些運(yùn)算符由參數(shù)控制，這些參數(shù)決定用于創(chuàng)建每個(gè)輸出的輸入和操作。盡管有這樣的組合特征，但它們是可微的，因此可以通過反向傳播來學(xué)習(xí)。

摘要

神經(jīng)網(wǎng)絡(luò)可以學(xué)習(xí)表示和操作數(shù)值信息，但它們很少能很好地推廣到訓(xùn)練中遇到的數(shù)值范圍之外。為了支持更系統(tǒng)的數(shù)值外推（numerical extrapolation），我們提出一種新的架構(gòu)，它將數(shù)值表示為線性激活函數(shù)，使用原始算術(shù)運(yùn)算符進(jìn)行操作，并由學(xué)習(xí)門（learned gates）控制。

我們將這個(gè)模塊稱為神經(jīng)算術(shù)邏輯單元（neural arithmetic logic unit, NALU），參照自傳統(tǒng)處理器中的算術(shù)邏輯單元。實(shí)驗(yàn)表明，NALU增強(qiáng)的神經(jīng)網(wǎng)絡(luò)可以學(xué)習(xí)跟蹤時(shí)間，對(duì)數(shù)字圖像執(zhí)行算術(shù)運(yùn)算，將數(shù)字語言轉(zhuǎn)化為實(shí)值標(biāo)量，執(zhí)行計(jì)算機(jī)代碼，以及對(duì)圖像中的對(duì)象進(jìn)行計(jì)數(shù)。與傳統(tǒng)架構(gòu)相比，我們?cè)谟?xùn)練期間的數(shù)值范圍內(nèi)和范圍外都得到了更好的泛化，外推經(jīng)常超出訓(xùn)練數(shù)值范圍幾個(gè)數(shù)量級(jí)之外。

這篇論文一經(jīng)發(fā)表即引起很多關(guān)注，有人認(rèn)為這篇論文比一眼看上去要更重要，Reddit用戶claytonkb表示：“結(jié)合最近的D2NN，我們可以構(gòu)建超低功耗的芯片，可以在恒定時(shí)間計(jì)算超級(jí)復(fù)雜的函數(shù)，我們很快就會(huì)轉(zhuǎn)向異構(gòu)計(jì)算架構(gòu)。”

很快有大神在Keras做出了NALU網(wǎng)絡(luò)的實(shí)現(xiàn)，感受一下：

https://github.com/kgrm/NALU

神經(jīng)累加器和神經(jīng)算術(shù)邏輯單元

算術(shù)邏輯單元（Arithmetic Logic Unit, ALU）是中央處理器的執(zhí)行單元，是所有中央處理器的核心組成部分，由與門和或門構(gòu)成的算數(shù)邏輯單元，主要功能是進(jìn)行二進(jìn)制的算術(shù)運(yùn)算，如加減乘。

在這篇論文中，研究者提出兩種能夠?qū)W習(xí)以系統(tǒng)的方式表示和操作數(shù)字的模型。第一種方法支持累加積累量（accumulate quantities additively）的能力，這是線性外推的理想歸納偏差。這個(gè)模型構(gòu)成了第二個(gè)模型的基礎(chǔ)，即支持乘法外推（multiplicative extrapolation）。該模型還說明了如何將任意算術(shù)函數(shù)的歸納偏差有效地合并到端到端模型中。

第一個(gè)模型是神經(jīng)累加器（Neural Accumulator，NAC），它是線性層的一種特殊情況，其變換矩陣W僅由-1，0和1組成；也就是說，它的輸出是輸入向量中行的加法或減法。這可以防止層在將輸入映射到輸出時(shí)更改數(shù)字表示的比例，這意味著無論將多少個(gè)操作鏈接在一起，它們?cè)谡麄€(gè)模型中都是一致的。我們通過以下方式鼓勵(lì)W內(nèi)的0，1和-1來改善簡單線性層的歸納偏差。

由于硬約束強(qiáng)制W的每個(gè)元素都是{-1,0,1}中的一個(gè)，這會(huì)使學(xué)習(xí)變得困難，我們提出W在無約束參數(shù)方面的連續(xù)和可微分參數(shù)化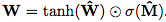：。 這種形式便于用梯度下降進(jìn)行學(xué)習(xí)，并產(chǎn)生矩陣，其元素保證在[-1,1]并且偏向接近-1,0或1。

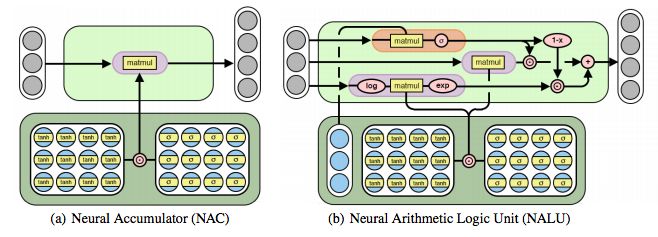
圖2：神經(jīng)累加器（NAC）是其輸入的線性變換。 變換矩陣是tanh（W）和σ（M）的元素乘積。 神經(jīng)算術(shù)邏輯單元（NALU）使用兩個(gè)帶有綁定權(quán)重的NAC來啟用加/減（較小的紫色cell）和乘法/除法（較大的紫色cell），由門（橙色的cell）控制

雖然加法和減法使得許多有用的系統(tǒng)泛化成為可能，但是可能需要學(xué)習(xí)更復(fù)雜的數(shù)學(xué)函數(shù)（例如乘法）的強(qiáng)健能力。 圖2描述了這樣一個(gè)單元：神經(jīng)算術(shù)邏輯單元（NALU），它學(xué)習(xí)兩個(gè)子單元之間的加權(quán)和，一個(gè)能夠執(zhí)行加法和減法，另一個(gè)能夠執(zhí)行乘法，除法和冪函數(shù)，如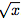。 重要的是，NALU演示了NAC如何通過門控子操作進(jìn)行擴(kuò)展，從而促進(jìn)了新類型數(shù)值函數(shù)的端到端學(xué)習(xí)。

NALU由兩個(gè)NAC單元（紫色單元）組成，這兩個(gè)單元由學(xué)習(xí)的S形門g（橙色單元）內(nèi)插，這樣如果加/減子單元的輸出值應(yīng)用權(quán)重為1（on），則乘法/除法子單元為0（off），反之亦然。 第一個(gè)NAC（較小的紫色子單元）計(jì)算累加向量a，存儲(chǔ)NALU的加法/減法運(yùn)算的結(jié)果; 它與原始NAC的計(jì)算方式相同（即a = Wx）。 第二個(gè)NAC（較大的紫色子單元）在對(duì)數(shù)空間中運(yùn)行，因此能夠?qū)W習(xí)乘法和除法，將結(jié)果存儲(chǔ)在m：

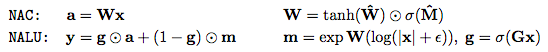
總之，這個(gè)單元可以學(xué)習(xí)由乘法，加法，減法，除法和冪函數(shù)組成的算術(shù)函數(shù)，其推斷方式是在訓(xùn)練期間觀察到的范圍之外的數(shù)字。

實(shí)驗(yàn)和結(jié)果

我們?cè)诙鄠€(gè)任務(wù)領(lǐng)域（合成、圖像、文本和代碼）、學(xué)習(xí)信號(hào)（監(jiān)督學(xué)習(xí)和強(qiáng)化學(xué)習(xí)）和結(jié)構(gòu)（前饋和循環(huán)）進(jìn)行實(shí)驗(yàn)。結(jié)果表明，我們提出的模型可以學(xué)習(xí)捕獲數(shù)據(jù)潛在數(shù)值性質(zhì)的表示函數(shù)，并將其推廣到比訓(xùn)練中觀察到的數(shù)值大幾個(gè)數(shù)量級(jí)的數(shù)值。我們還觀察到，即使不需要外推，我們的模塊相對(duì)于線性層也顯示出優(yōu)越的計(jì)算偏差。在一種情況下，我們的模型在誤差率上超過了最先進(jìn)的圖像計(jì)數(shù)網(wǎng)絡(luò)54%。

任務(wù)1：簡單的函數(shù)學(xué)習(xí)任務(wù)

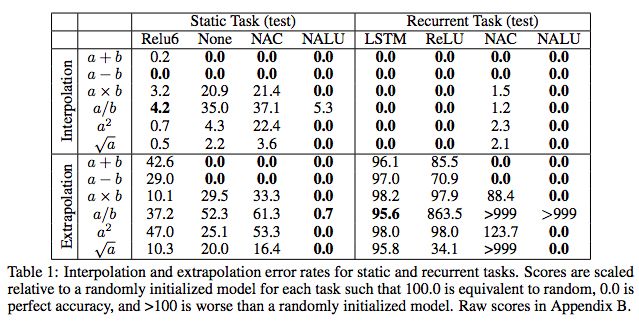
表1：靜態(tài)和循環(huán)任務(wù)的插值和外推誤差率。

任務(wù)2；MNIST計(jì)數(shù)和算術(shù)任務(wù)

表2：長度為1,10,100和1000的序列的MNIST計(jì)數(shù)和加法任務(wù)的準(zhǔn)確度。

結(jié)果顯示，NAC和NALU都能很好地推斷和插值。

任務(wù)3：語言到數(shù)字的翻譯任務(wù)

表3：將數(shù)字串轉(zhuǎn)換為標(biāo)量的平均絕對(duì)誤差（MAE）比較。

圖3：對(duì)先前未見過的查詢的中間NALU預(yù)測(cè)。

圖3顯示了隨機(jī)選擇的測(cè)試實(shí)例中NALU的中間狀態(tài)。 在沒有監(jiān)督的情況下，模型學(xué)會(huì)跟蹤當(dāng)前token的未知數(shù)的合理估計(jì)，這允許網(wǎng)絡(luò)預(yù)測(cè)它以前從未見過的token。

程序評(píng)估

圖4：簡單的程序評(píng)估，外推到更大的值。

我們比較了三種流行的RNN（UGRNN，LSTM和DNC），結(jié)果顯示即使域增加了兩個(gè)數(shù)量級(jí)，外推也是穩(wěn)定的。

學(xué)習(xí)在網(wǎng)格世界環(huán)境中跟蹤時(shí)間

圖5 :（上）Grid-World環(huán)境中時(shí)間跟蹤任務(wù)的幀。 智能體（灰色）必須在指定時(shí)間移動(dòng)到目的地（紅色）。 （下）NAC提高了A3C智能體所學(xué)到的外推能力。

MNIST奇偶校驗(yàn)預(yù)測(cè)任務(wù)和消融研究

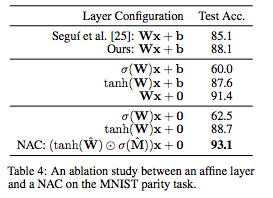
表4：關(guān)于MNIST奇偶校驗(yàn)任務(wù)的affine層和NAC之間的消融研究。

表4總結(jié)了變體模型的性能。結(jié)果顯示，去除偏差并對(duì)權(quán)重應(yīng)用非線性顯著提高了端到端模型的準(zhǔn)確性，即使大多數(shù)參數(shù)不在NAC中，NAC將先前最佳結(jié)果的誤差減少了54％。

結(jié)論

目前神經(jīng)網(wǎng)絡(luò)中數(shù)值模擬的方法還不夠完善，因?yàn)閿?shù)值表示方法不能推廣到訓(xùn)練中觀察到的范圍之外。我們已經(jīng)展示了NAC和NALU是如何在廣泛的任務(wù)領(lǐng)域中糾正這兩個(gè)缺點(diǎn)的，它促進(jìn)了數(shù)字表示和在訓(xùn)練過程中觀察到的范圍之外的數(shù)值表示函數(shù)。然而，NAC或NALU不太可能是每個(gè)任務(wù)的完美解決方案。相反，它們舉例說明了一種通用設(shè)計(jì)策略，用于創(chuàng)建具有針對(duì)目標(biāo)函數(shù)類的偏差的模型。這種設(shè)計(jì)策略是通過我們提出的單神經(jīng)元數(shù)值表示（single-neuron number representation）來實(shí)現(xiàn)的，它允許將任意（可微的）數(shù)值函數(shù)添加到模塊中，并通過學(xué)習(xí)門控制，正如NALU在加法/減法和乘法/除法之間實(shí)現(xiàn)的那樣。