在機器學習中，支持向量機（SVM）算法是針對二分類任務設計的，可以分析數據，識別模式，用于分類和回歸分析。訓練算法構建一個模型，將新示例分配給一個類別或另一個類別，使其成為非概率二元線性分類器；使用核技術還可以有效地執行非線性分類。迄今為止線性核技術仍是文本分類的首選技術。

今天，人工智能頭條將首先從支持向量機的基礎理論知識入手，和大家探討一個良好的排序算法如何在解決 SVM 問題過程中，在機器學習技術中發揮的重要作用。

▌前言

當前，機器學習(ML)正在迅速成為現實社會中最重要的計算技術之一。作為人工智能(AI)的一個分支，這項技術適用于諸多領域，包括自然語言翻譯和處理領域(如Siri和Alexa)、醫學研究，自動駕駛及商業戰略發展等。一些令人眼花繚亂的算法正在被不斷創造來解決ML問題，并從數據流中學習模式以構建AI的基礎設施。

然而，有時候我們需要回頭思考并分析一些基本算法是如何在這場機器學習革命中發揮作用及其所帶來的影響。下面我就舉一個非常重要的案例。

▌支持向量機

支持向量機(SVM)是過去幾十年發展中出現的最重要的機器學習技術之一。它的核心思想是給定一組訓練樣本，每個樣本標記屬于二分類中的一類，SVM將構建一個用于對一個新的樣本進行分類的模型，也就是說，它其實是一個非概率的二元線性分類器，廣泛用于工業系統，文本分類，模式識別，生物ML應用等。

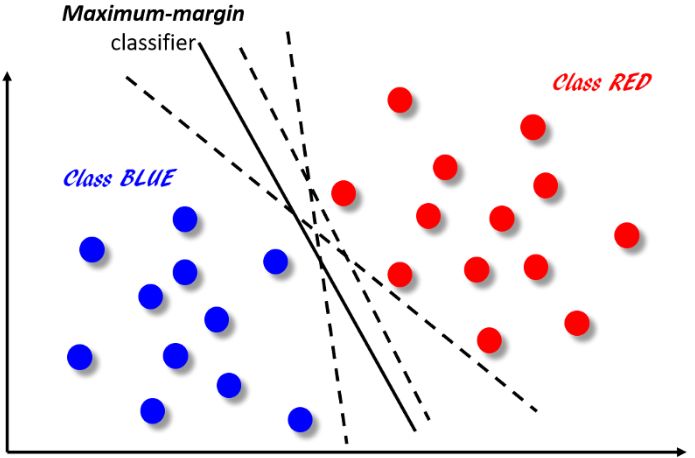
SVM的核心思想主要如下圖所示，它的最終目標是將二維平面中的點分為紅藍兩類，這可以通過在兩組點集之間創建分類器邊界(利用分類算法從帶標記的數據中學習邊界信息)來實現。下圖中展示了一些可能的分類器，它們都將正確地對數據點進行分類，但并非所有分類器都能使得分類后最接近邊界的數據點具有相同的邊距(距離)。從下圖中我們可以看出，其中只有一個分類器能夠最大化紅色和藍色點之間的距離，我們用實線表示該分類器而用虛線表示其他分類器。這種邊距最大化的效用是盡可能地放大兩個類別之間的距離，以便對新的點分類時分類器的泛化誤差盡可能小。

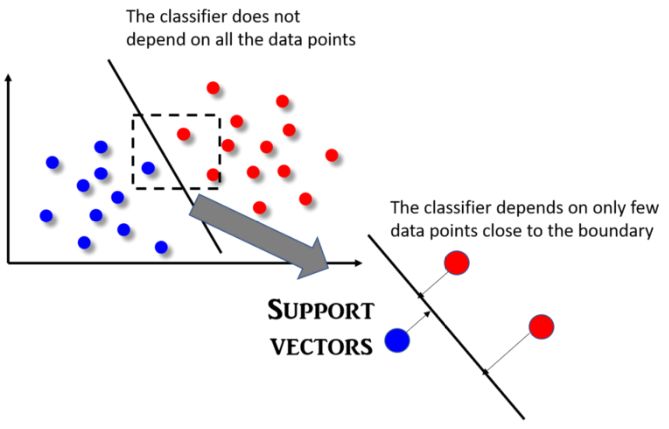
SVM算法最明顯的特征是分類器不依賴于所有數據點，這不同于依賴每個數據點特征并將其用于構造分類器邊界函數的邏輯回歸算法。實際上，SVM分類器會依賴于一個非常小的子數據點集，這些數據點最接近邊界，同時它們在超平面中的位置可以影響分類器邊界線。由這些點構成的向量唯一地定義并支持分類器函數，因此我們把這種分類器稱之為“支持向量機”，它的概念圖解如下圖所示。

這里，我們為大家準備了一個關于 SVM的精彩視頻教程。

▌關于SVM工作背后的幾何解釋：Convex Hull

SVM算法背后的形式數學相當復雜，但從直觀地我們可以理解為這是一種稱為 Convex Hull 的特殊幾何結構。

什么是Convex Hull呢？形式上，在歐幾里德平面（Euclidean plan）或歐幾里德空間（Euclidean space）中的一組 X點的凸包（convex hull）或凸殼（convex envelope）或閉包（convex closure），是包含 X點的最小凸集。我們可以通過類比“橡皮筋”來更容易地理解這個概念。想象一下，橡皮筋在一組釘子（類比我們的感興趣點）周圍伸展。如果橡皮筋被釋放，它會纏繞在釘子周圍，從而形成一個緊密的邊界，這是我們開始定義的集合。由此產生的形狀就是凸包，我們可以通過那些由橡皮筋產生的邊界釘子集來描述它，下面的圖解將有助于更直觀地感受這個概念。

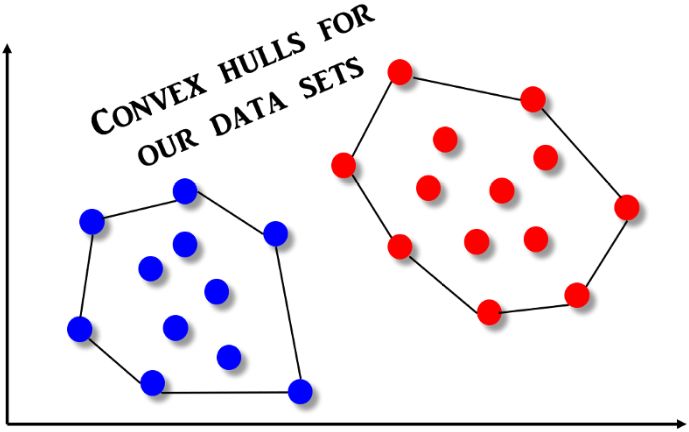
現在，我們可以很容易想象SVM分類器只不過是一種線性分類器，它通過二分法將連接這些凸包的線一分為二。因此，確定SVM分類器也就解決了找到一組點的凸包問題。

▌那么，如何確定凸包呢？

我們通過下面這個動畫來說明這個問題！這里，我將展示用于確定一組點的凸包的Graham’s scan算法。該算法能夠沿著凸包的邊界順序，依次找到其所有的頂點，并通過堆棧的方法有效地檢測和去除邊界中的凹陷區域。

現在還有個問題是這種算法的效率如何，即Grahan’s scan算法的時間復雜度是多少呢？

事實證明，Grahan’s scan算法的時間復雜性取決于它用于尋找構成凸包的正確點集的基礎排序算法。但是，一開始的排序算法又是什么呢？

Grahan’s scan算法的基本思想來自凸包的兩種特性：

只能通過逆時針轉動來橫穿凸包區域

關于具有最低y坐標的點p而言，凸包的頂點將以極角遞增的順序出現。

首先，這些點以數組 points的形式存儲。因此，算法由定位的參考點開始，這是具有最低 y坐標的點（在有捆綁關系(ties)的情況下，我們通過選擇具有最低 x和 y坐標的點來解綁）。一旦我們找到參考點，我們可以將該點移動到數組 points的開頭，使其與數組中第一個點互換位置。

接著，利用剩余點相對于參考點的極角關系，我們對其進行排序。經過排序后，相對于參考點的極角最小點將位于數組的開始處，而具有最大的極角點將位于數組的末尾。

隨著所有的點都被正確地排序，現在我們可以運行算法的主循環部分。當我們處理主數組中的點時，循環并將增長和縮小第二個列表。基本上，如果我們順時針地旋轉點，那么這些點將被推到堆棧上；反之，則如果我們以逆時針地方向，則拒絕并從堆棧彈出這些點。第二個列表一開始是個空列表，在算法結束時，構成凸邊界的點將出現在此列表中。堆棧數據結構正用于此目的。

#Threepointsareacounter-clockwiseturnifccw>0,clockwiseif#ccw

因此，Graham’s scan算法的時間復雜度取決于排序算法的效率。我們可以使用任何通用的排序算法，但對于時間復雜度為 O (n^2)和 O (n.log(n))的算法而言（如下面的動畫所示），它們之間的 Graham’s scan算法的效率存在很大差異。

▌總結

在本文中，我們展示了簡單排序算法在解決 SVM 問題過程中發揮的作用，以及它與廣泛使用的機器學習技術之間的關系。雖然有許多基于離散優化的算法可以用來解決SVM問題，但在構建復雜的AI學習模型方面，這種方法被視為是一種重要而基礎高效的算法。