1、背景

特征組合的挑戰

對于一個基于CTR預估的推薦系統，最重要的是學習到用戶點擊行為背后隱含的特征組合。在不同的推薦場景中，低階組合特征或者高階組合特征可能都會對最終的CTR產生影響。

之前介紹的因子分解機(Factorization Machines, FM)通過對于每一維特征的隱變量內積來提取特征組合。最終的結果也非常好。但是，雖然理論上來講FM可以對高階特征組合進行建模，但實際上因為計算復雜度的原因一般都只用到了二階特征組合。

那么對于高階的特征組合來說，我們很自然的想法，通過多層的神經網絡即DNN去解決。

DNN的局限

下面的圖片來自于張俊林教授在AI大會上所使用的PPT。

我們之前也介紹過了，對于離散特征的處理，我們使用的是將特征轉換成為one-hot的形式，但是將One-hot類型的特征輸入到DNN中，會導致網絡參數太多：

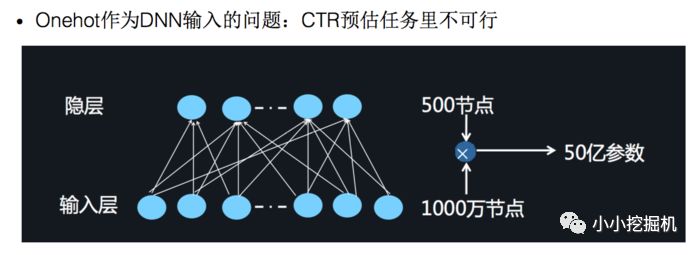
如何解決這個問題呢，類似于FFM中的思想，將特征分為不同的field：

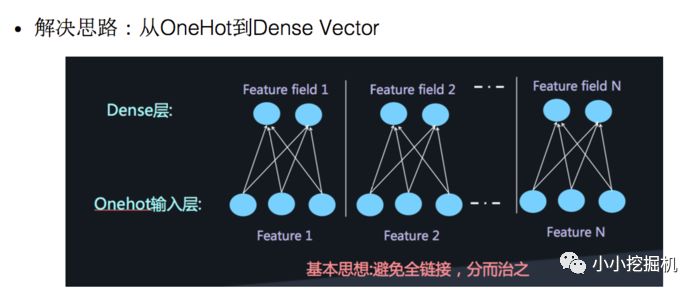
再加兩層的全鏈接層，讓Dense Vector進行組合，那么高階特征的組合就出來了

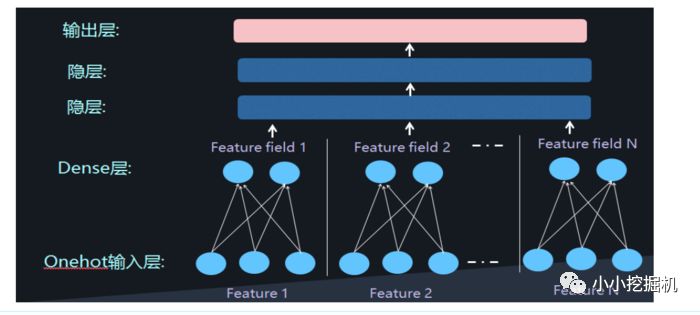
但是低階和高階特征組合隱含地體現在隱藏層中，如果我們希望把低階特征組合單獨建模，然后融合高階特征組合。

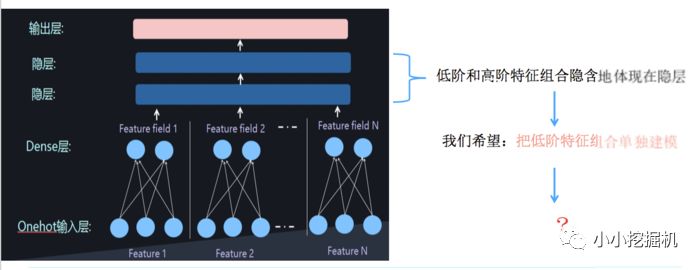
即將DNN與FM進行一個合理的融合：

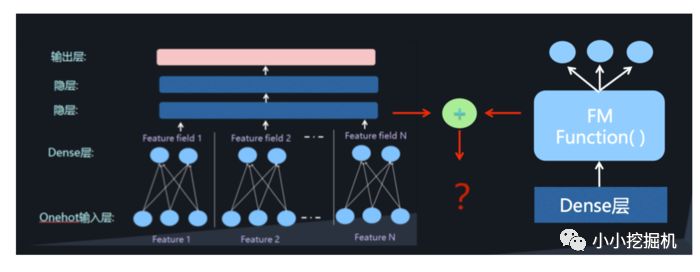
二者的融合總的來說有兩種形式，一是串行結構，二是并行結構

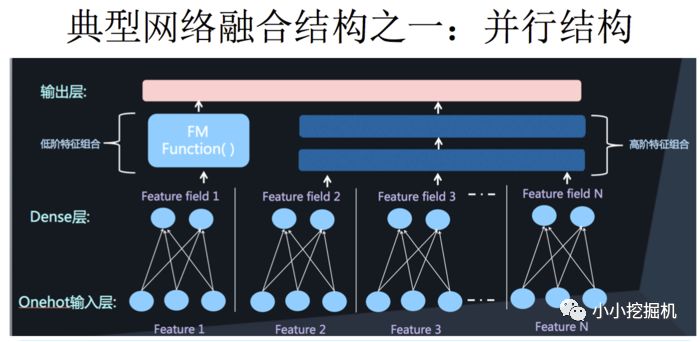
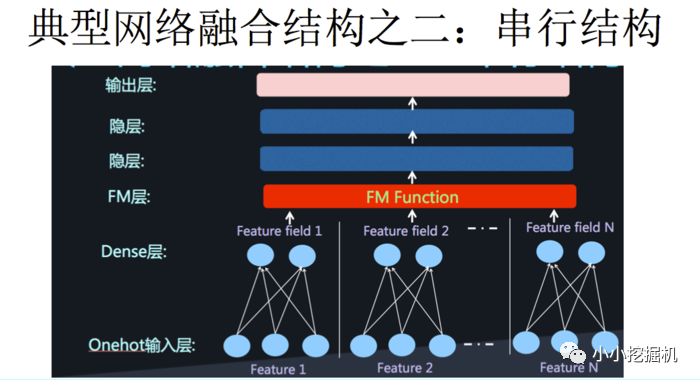
而我們今天要講到的DeepFM，就是并行結構中的一種典型代表。

2、DeepFM模型

我們先來看一下DeepFM的模型結構：

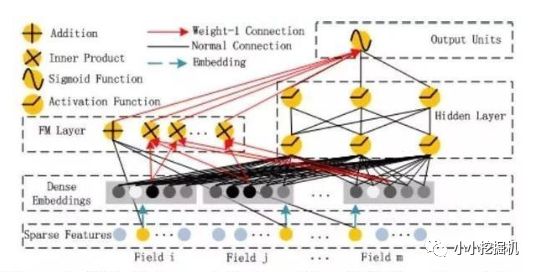
DeepFM包含兩部分：神經網絡部分與因子分解機部分，分別負責低階特征的提取和高階特征的提取。這兩部分共享同樣的輸入。DeepFM的預測結果可以寫為：

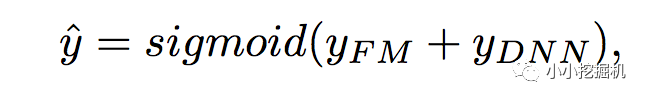
FM部分

FM部分的詳細結構如下：

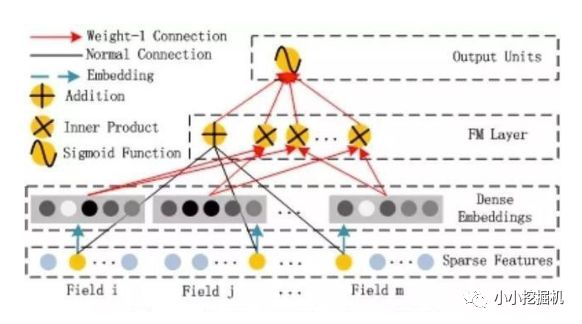
FM部分是一個因子分解機。關于因子分解機可以參閱文章[Rendle, 2010] Steffen Rendle. Factorization machines. In ICDM, 2010.。因為引入了隱變量的原因，對于幾乎不出現或者很少出現的隱變量，FM也可以很好的學習。

FM的輸出公式為：

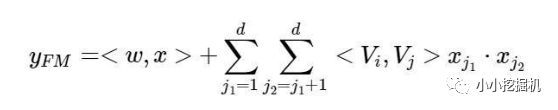
深度部分

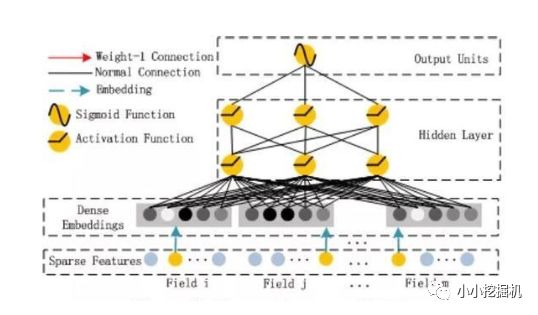
深度部分是一個前饋神經網絡。與圖像或者語音這類輸入不同，圖像語音的輸入一般是連續而且密集的，然而用于CTR的輸入一般是及其稀疏的。因此需要重新設計網絡結構。具體實現中為，在第一層隱含層之前，引入一個嵌入層來完成將輸入向量壓縮到低維稠密向量。

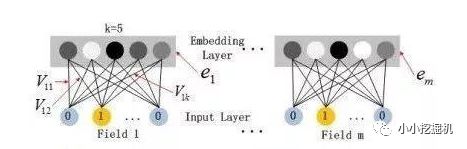
嵌入層(embedding layer)的結構如上圖所示。當前網絡結構有兩個有趣的特性，1）盡管不同field的輸入長度不同，但是embedding之后向量的長度均為K。2)在FM里得到的隱變量Vik現在作為了嵌入層網絡的權重。

這里的第二點如何理解呢，假設我們的k=5，首先，對于輸入的一條記錄，同一個field 只有一個位置是1，那么在由輸入得到dense vector的過程中，輸入層只有一個神經元起作用，得到的dense vector其實就是輸入層到embedding層該神經元相連的五條線的權重，即vi1，vi2，vi3，vi4，vi5。這五個值組合起來就是我們在FM中所提到的Vi。在FM部分和DNN部分，這一塊是共享權重的，對同一個特征來說，得到的Vi是相同的。

有關模型具體如何操作，我們可以通過代碼來進一步加深認識。

3、相關知識

我們先來講兩個代碼中會用到的相關知識吧，代碼是參考的github上星數最多的DeepFM實現代碼。

Gini Normalization

代碼中將CTR預估問題設定為一個二分類問題，繪制了Gini Normalization來評價不同模型的效果。這個是什么東西，不太懂，百度了很多，發現了一個比較通俗易懂的介紹。

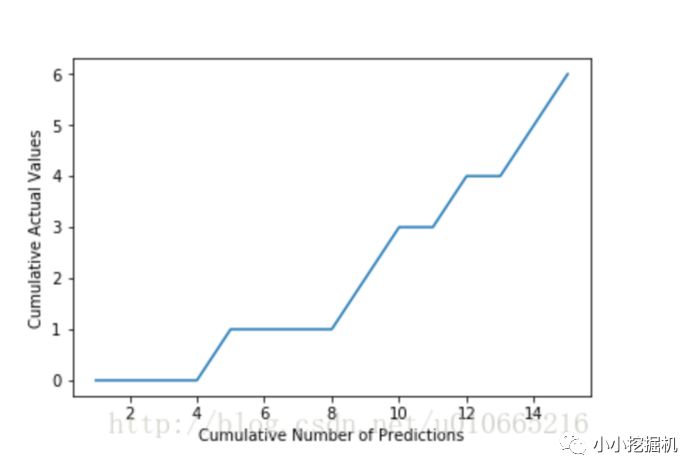
假設我們有下面兩組結果，分別表示預測值和實際值：

predictions = [0.9, 0.3, 0.8, 0.75, 0.65, 0.6, 0.78, 0.7, 0.05, 0.4, 0.4, 0.05, 0.5, 0.1, 0.1]actual = [1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]

然后我們將預測值按照從小到大排列，并根據索引序對實際值進行排序：

Sorted Actual Values [0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1]

然后，我們可以畫出如下的圖片：

接下來我們將數據Normalization到0，1之間。并畫出45度線。

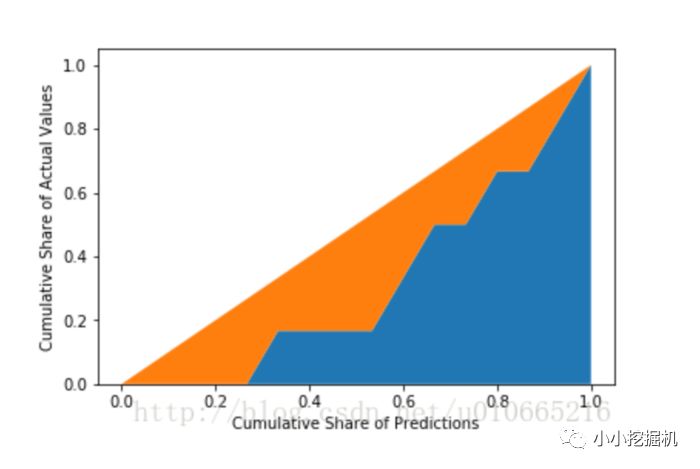
橙色區域的面積，就是我們得到的Normalization的Gini系數。

這里，由于我們是將預測概率從小到大排的，所以我們希望實際值中的0盡可能出現在前面，因此Normalization的Gini系數越大，分類效果越好。

embedding_lookup

在tensorflow中有個embedding_lookup函數，我們可以直接根據一個序號來得到一個詞或者一個特征的embedding值，那么他內部其實是包含一個網絡結構的，如下圖所示：

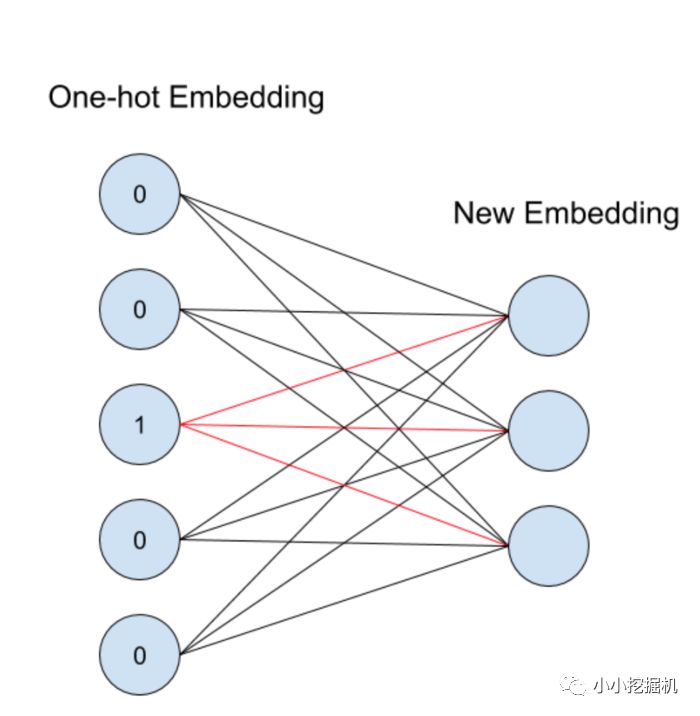
假設我們想要找到2的embedding值，這個值其實是輸入層第二個神經元與embedding層連線的權重值。

之前有大佬跟我探討word2vec輸入的問題，現在也算是有個比較明確的答案，輸入其實就是one-hot Embedding，而word2vec要學習的是new Embedding。

4、代碼解析

好，一貫的風格，先來介紹幾個地址：原代碼地址：https://github.com/ChenglongChen/tensorflow-DeepFM本文代碼地址：https://github.com/princewen/tensorflow_practice/tree/master/Basic-DeepFM-model數據下載地址：https://www.kaggle.com/c/porto-seguro-safe-driver-prediction

好了，話不多說，我們來看看代碼目錄吧，接下來，我們將主要對網絡的構建進行介紹，而對數據的處理，流程的控制部分，相信大家根據代碼就可以看懂。

項目結構

項目結構如下：

其實還應該有一個存放data的路徑。config.py保存了我們模型的一些配置。DataReader對數據進行處理，得到模型可以使用的輸入。DeepFM是我們構建的模型。main是項目的入口。metrics是計算normalized gini系數的代碼。

模型輸入

模型的輸入主要有下面幾個部分：

self.feat_index = tf.placeholder(tf.int32, shape=[None,None], name='feat_index')self.feat_value = tf.placeholder(tf.float32, shape=[None,None], name='feat_value')self.label = tf.placeholder(tf.float32,shape=[None,1],name='label')self.dropout_keep_fm = tf.placeholder(tf.float32,shape=[None],name='dropout_keep_fm')self.dropout_keep_deep = tf.placeholder(tf.float32,shape=[None],name='dropout_deep_deep')

feat_index是特征的一個序號，主要用于通過embedding_lookup選擇我們的embedding。feat_value是對應的特征值，如果是離散特征的話，就是1，如果不是離散特征的話，就保留原來的特征值。label是實際值。還定義了兩個dropout來防止過擬合。

權重構建

權重的設定主要有兩部分，第一部分是從輸入到embedding中的權重，其實也就是我們的dense vector。另一部分就是深度神經網絡每一層的權重。第二部分很好理解，我們主要來看看第一部分：

#embeddingsweights['feature_embeddings'] = tf.Variable( tf.random_normal([self.feature_size,self.embedding_size],0.0,0.01), name='feature_embeddings')weights['feature_bias'] = tf.Variable(tf.random_normal([self.feature_size,1],0.0,1.0),name='feature_bias')

weights['feature_embeddings'] 存放的每一個值其實就是FM中的vik，所以它是N * F * K的。其中N代表數據量的大小，F代表feture的大小(將離散特征轉換成one-hot之后的特征總量),K代表dense vector的大小。

weights['feature_bias']是FM中的一次項的權重。

Embedding part

這個部分很簡單啦，是根據feat_index選擇對應的weights['feature_embeddings']中的embedding值，然后再與對應的feat_value相乘就可以了：

# modelself.embeddings = tf.nn.embedding_lookup(self.weights['feature_embeddings'],self.feat_index) # N * F * Kfeat_value = tf.reshape(self.feat_value,shape=[-1,self.field_size,1])self.embeddings = tf.multiply(self.embeddings,feat_value)

FM part

首先來回顧一下我們之前對FM的化簡公式，之前去今日頭條面試還問到過公式的推導。

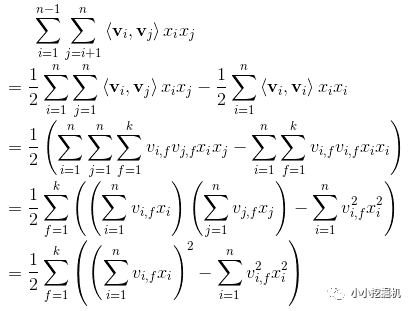
所以我們的二次項可以根據化簡公式輕松的得到，再加上我們的一次項，FM的part就算完了。同時更為方便的是，由于權重共享，我們這里可以直接用Embedding part計算出的embeddings來得到我們的二次項：

# first order termself.y_first_order = tf.nn.embedding_lookup(self.weights['feature_bias'],self.feat_index)self.y_first_order = tf.reduce_sum(tf.multiply(self.y_first_order,feat_value),2)self.y_first_order = tf.nn.dropout(self.y_first_order,self.dropout_keep_fm[0])# second order term# sum-square-partself.summed_features_emb = tf.reduce_sum(self.embeddings,1) # None * kself.summed_features_emb_square = tf.square(self.summed_features_emb) # None * K# squre-sum-partself.squared_features_emb = tf.square(self.embeddings)self.squared_sum_features_emb = tf.reduce_sum(self.squared_features_emb, 1) # None * K#second orderself.y_second_order = 0.5 * tf.subtract(self.summed_features_emb_square,self.squared_sum_features_emb)self.y_second_order = tf.nn.dropout(self.y_second_order,self.dropout_keep_fm[1])

DNN part

DNNpart的話，就是將Embedding part的輸出再經過幾層全鏈接層：

# Deep componentself.y_deep = tf.reshape(self.embeddings,shape=[-1,self.field_size * self.embedding_size])self.y_deep = tf.nn.dropout(self.y_deep,self.dropout_keep_deep[0])for i in range(0,len(self.deep_layers)): self.y_deep = tf.add(tf.matmul(self.y_deep,self.weights["layer_%d" %i]), self.weights["bias_%d"%I]) self.y_deep = self.deep_layers_activation(self.y_deep) self.y_deep = tf.nn.dropout(self.y_deep,self.dropout_keep_deep[i+1])

最后，我們要將DNN和FM兩部分的輸出進行結合：

concat_input = tf.concat([self.y_first_order, self.y_second_order, self.y_deep], axis=1)

損失及優化器

我們可以使用logloss(如果定義為分類問題)，或者mse(如果定義為預測問題)，以及多種的優化器去進行嘗試，這些根據不同的參數設定得到：

# lossif self.loss_type == "logloss": self.out = tf.nn.sigmoid(self.out) self.loss = tf.losses.log_loss(self.label, self.out)elif self.loss_type == "mse": self.loss = tf.nn.l2_loss(tf.subtract(self.label, self.out))# l2 regularization on weightsif self.l2_reg > 0: self.loss += tf.contrib.layers.l2_regularizer( self.l2_reg)(self.weights["concat_projection"]) if self.use_deep: for i in range(len(self.deep_layers)): self.loss += tf.contrib.layers.l2_regularizer( self.l2_reg)(self.weights["layer_%d" % I])if self.optimizer_type == "adam": self.optimizer = tf.train.AdamOptimizer(learning_rate=self.learning_rate, beta1=0.9, beta2=0.999, epsilon=1e-8).minimize(self.loss)elif self.optimizer_type == "adagrad": self.optimizer = tf.train.AdagradOptimizer(learning_rate=self.learning_rate, initial_accumulator_value=1e-8).minimize(self.loss)elif self.optimizer_type == "gd": self.optimizer = tf.train.GradientDescentOptimizer(learning_rate=self.learning_rate).minimize(self.loss)elif self.optimizer_type == "momentum": self.optimizer = tf.train.MomentumOptimizer(learning_rate=self.learning_rate, momentum=0.95).minimize( self.loss)

模型效果

前面提到了，我們用logloss作為損失函數去進行模型的參數更新，但是代碼中輸出了模型的 Normalization 的 Gini值來進行模型評價，我們可以對比一下(記住，Gini值越大越好呦)：

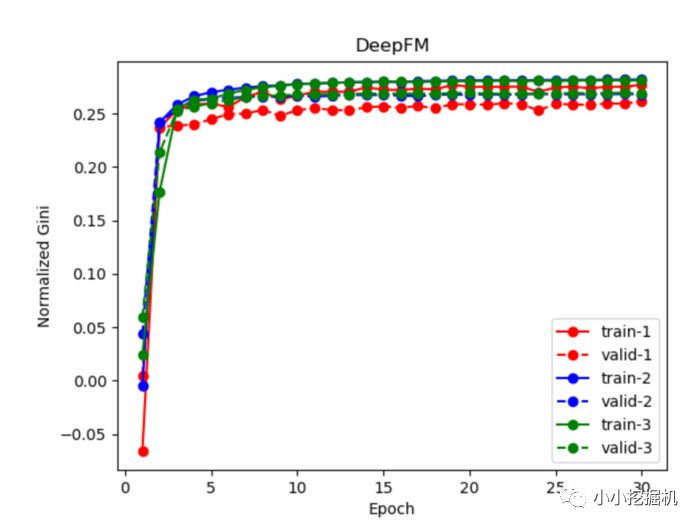
好啦，本文只是提供一個引子，有關DeepFM更多的知識大家可以更多的進行學習呦。