卡爾曼濾波器是傳感器融合工程師用于自動駕駛汽車的工具。想象一下,你有一個雷達傳感器,告訴你另一輛車距離15米,一個激光傳感器說車輛距離20米。你如何協調這些傳感器測量?這就是卡爾曼濾波器的功能。卡爾曼濾波在自動駕駛汽車上的應用十分廣泛,本文講述卡爾曼濾波算法,希望對你有所幫助。
卡爾曼濾波算法在控制領域有極廣泛的應用,在發動機燃油噴射控制中,可以應用擴展的卡爾曼濾波理論研究瞬態工況下發動機循環進氣量的最優估計算法,在雷達中,人們感興趣的是跟蹤目標,但目標的位置、速度、加速度的測量值往往在任何時候都有噪聲。卡爾曼濾波利用目標的動態信息,設法去掉噪聲的影響,得到一個關于目標位置的好的估計。
為了以后更好的工程實踐應用卡爾曼濾波算法,今天小編帶領著大家了解卡爾曼濾波算法的理論。
什么是卡爾曼濾波?
你可以在任何含有不確定信息的動態系統中使用卡爾曼濾波,對系統下一步的走向做出有根據的預測,即使伴隨著各種干擾,卡爾曼濾波總是能指出真實發生的情況。
在連續變化的系統中使用卡爾曼濾波是非常理想的,它具有占用內存小的優點(除了前一個狀態量外,不需要保留其它歷史數據),并且速度很快,很適合應用于實時問題和嵌入式系統。
在Google上找到的大多數關于實現卡爾曼濾波的數學公式看起來有點晦澀難懂,這個狀況有點糟糕。實際上,如果以正確的方式看待它,卡爾曼濾波是非常簡單和容易理解的,下面我將用漂亮的圖片和色彩清晰的闡述它,你只需要懂一些基本的概率和矩陣的知識就可以了。
我們能用卡爾曼濾波做什么?
用玩具舉例:你開發了一個可以在樹林里到處跑的小機器人,這個機器人需要知道它所在的確切位置才能導航。
我們可以說機器人有一個狀態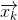 ,表示位置和速度:?
,表示位置和速度:?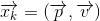
注意這個狀態只是關于這個系統基本屬性的一堆數字,它可以是任何其它的東西。在這個例子中是位置和速度,它也可以是一個容器中液體的總量,汽車發動機的溫度,用戶手指在觸摸板上的位置坐標,或者任何你需要跟蹤的信號。
這個機器人帶有GPS,精度大約為10米,還算不錯,但是,它需要將自己的位置精確到10米以內。樹林里有很多溝壑和懸崖,如果機器人走錯了一步,就有可能掉下懸崖,所以只有GPS是不夠的。
或許我們知道一些機器人如何運動的信息:例如,機器人知道發送給電機的指令,知道自己是否在朝一個方向移動并且沒有人干預,在下一個狀態,機器人很可能朝著相同的方向移動。當然,機器人對自己的運動是一無所知的:它可能受到風吹的影響,輪子方向偏了一點,或者遇到不平的地面而翻倒。所以,輪子轉過的長度并不能精確表示機器人實際行走的距離,預測也不是很完美。
GPS傳感器告訴了我們一些狀態信息,我們的預測告訴了我們機器人會怎樣運動,但都只是間接的,并且伴隨著一些不確定和不準確性。但是,如果使用所有對我們可用的信息,我們能得到一個比任何依據自身估計更好的結果嗎?回答當然是YES,這就是卡爾曼濾波的用處。
卡爾曼濾波是如何看到你的問題的?
下面我們繼續以只有位置和速度這兩個狀態的簡單例子做解釋。
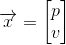
我們并不知道實際的位置和速度,它們之間有很多種可能正確的組合,但其中一些的可能性要大于其它部分:
卡爾曼濾波假設兩個變量(位置和速度,在這個例子中)都是隨機的,并且服從高斯分布。每個變量都有一個均值μ,表示隨機分布的中心(最可能的狀態),以及方差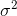 ,表示不確定性。?
,表示不確定性。?
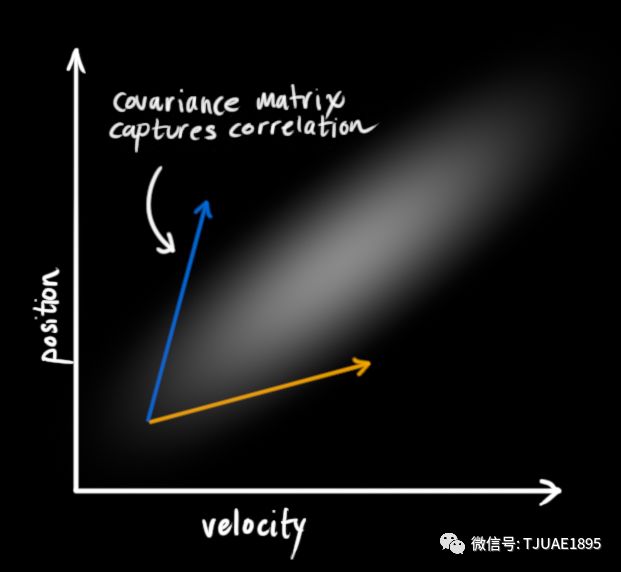
在上圖中,位置和速度是不相關的,這意味著由其中一個變量的狀態無法推測出另一個變量可能的值。下面的例子更有趣:位置和速度是相關的,觀測特定位置的可能性取決于當前的速度:
這種情況是有可能發生的,例如,我們基于舊的位置來估計新位置。如果速度過高,我們可能已經移動很遠了。如果緩慢移動,則距離不會很遠。跟蹤這種關系是非常重要的,因為它帶給我們更多的信息:其中一個測量值告訴了我們其它變量可能的值,這就是卡爾曼濾波的目的,盡可能地在包含不確定性的測量數據中提取更多信息!
這種相關性用協方差矩陣來表示,簡而言之,矩陣中的每個元素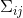 ?表示第 i 個和第 j 個狀態變量之間的相關度。(你可能已經猜到協方差矩陣是一個對稱矩陣,這意味著可以任意交換 i 和 j)。協方差矩陣通常用“
?表示第 i 個和第 j 個狀態變量之間的相關度。(你可能已經猜到協方差矩陣是一個對稱矩陣,這意味著可以任意交換 i 和 j)。協方差矩陣通常用“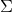 ”來表示,其中的元素則表示為“
”來表示,其中的元素則表示為“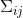 ?”。?
?”。?
使用矩陣來描述問題
我們基于高斯分布來建立狀態變量,所以在時刻 k 需要兩個信息:最佳估計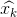 (即均值,其它地方常用 μ 表示),以及協方差矩陣?
(即均值,其它地方常用 μ 表示),以及協方差矩陣?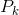 ?。?
?。?
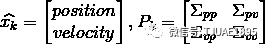 (1)
(1)
(當然,在這里我們只用到了位置和速度,實際上這個狀態可以包含多個變量,代表任何你想表示的信息)。接下來,我們需要根據當前狀態(k-1時刻)來預測下一狀態(k時刻)。記住,我們并不知道對下一狀態的所有預測中哪個是“真實”的,但我們的預測函數并不在乎。它對所有的可能性進行預測,并給出新的高斯分布。
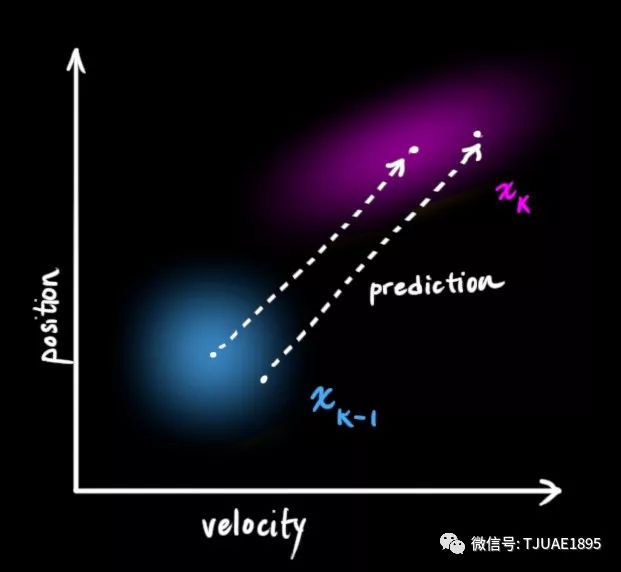
我們可以用矩陣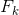 ?來表示這個預測過程:?
?來表示這個預測過程:?
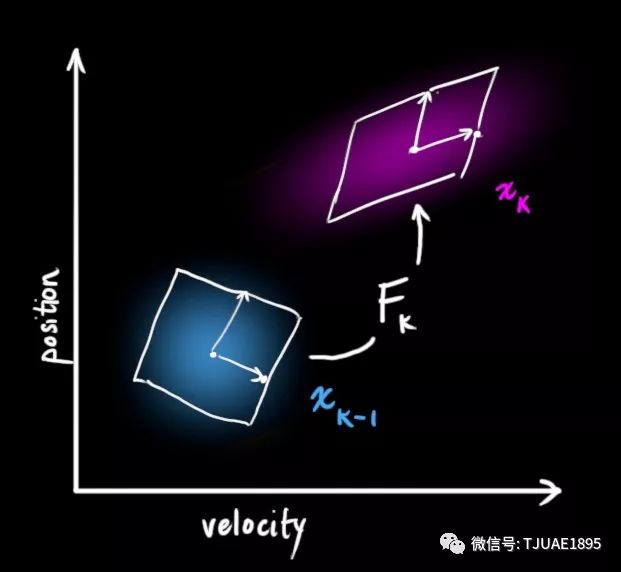
它將我們原始估計中的每個點都移動到了一個新的預測位置,如果原始估計是正確的話,這個新的預測位置就是系統下一步會移動到的位置。那我們又如何用矩陣來預測下一個時刻的位置和速度呢?下面用一個基本的運動學公式來表示:
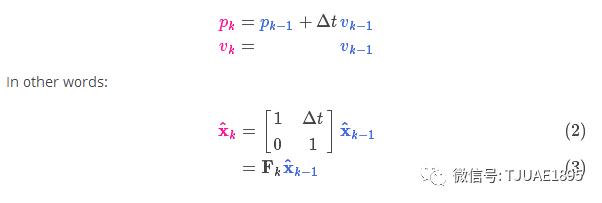
現在,我們有了一個預測矩陣來表示下一時刻的狀態,但是,我們仍然不知道怎么更新協方差矩陣。此時,我們需要引入另一個公式,如果我們將分布中的每個點都乘以矩陣A,那么它的協方差矩陣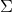 ?會怎樣變化呢?很簡單,下面給出公式:?
?會怎樣變化呢?很簡單,下面給出公式:?
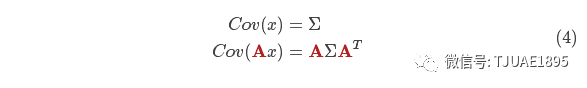
結合方程(4)和(3)得到:
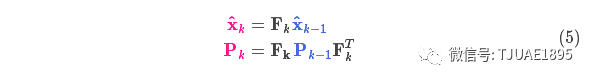
外部控制量
我們并沒有捕捉到一切信息,可能存在外部因素會對系統進行控制,帶來一些與系統自身狀態沒有相關性的改變。
以火車的運動狀態模型為例,火車司機可能會操縱油門,讓火車加速。相同地,在我們機器人這個例子中,導航軟件可能會發出一個指令讓輪子轉向或者停止。如果知道這些額外的信息,我們可以用一個向量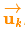 來表示,將它加到我們的預測方程中做修正。?
來表示,將它加到我們的預測方程中做修正。?
假設由于油門的設置或控制命令,我們知道了期望的加速度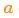 ,根據基本的運動學方程可以得到:?
,根據基本的運動學方程可以得到:?
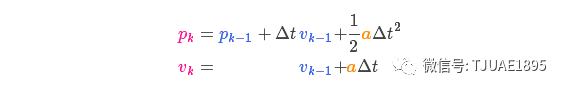
以矩陣的形式表示就是:
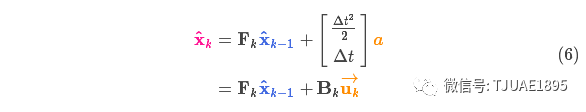
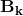 稱為控制矩陣,
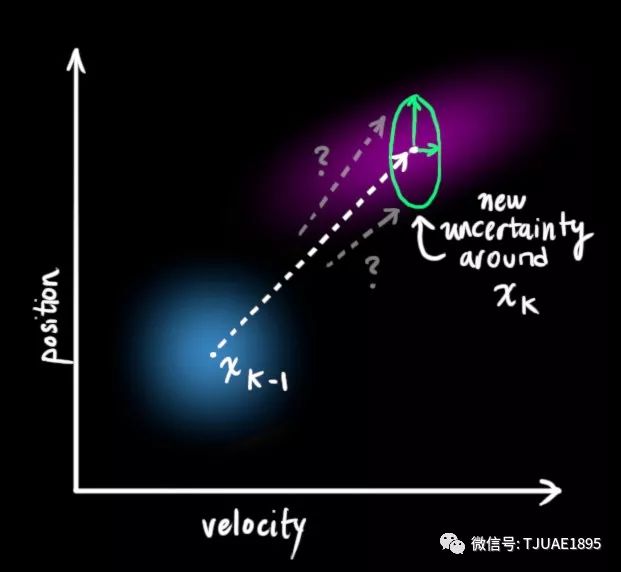
稱為控制矩陣,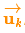 稱為控制向量(對于沒有外部控制的簡單系統來說,這部分可以忽略)。讓我們再思考一下,如果我們的預測并不是100%準確的,該怎么辦呢?
稱為控制向量(對于沒有外部控制的簡單系統來說,這部分可以忽略)。讓我們再思考一下,如果我們的預測并不是100%準確的,該怎么辦呢?
外部干擾
如果這些狀態量是基于系統自身的屬性或者已知的外部控制作用來變化的,則不會出現什么問題。
但是,如果存在未知的干擾呢?例如,假設我們跟蹤一個四旋翼飛行器,它可能會受到風的干擾,如果我們跟蹤一個輪式機器人,輪子可能會打滑,或者路面上的小坡會讓它減速。這樣的話我們就不能繼續對這些狀態進行跟蹤,如果沒有把這些外部干擾考慮在內,我們的預測就會出現偏差。
在每次預測之后,我們可以添加一些新的不確定性來建立這種與“外界”(即我們沒有跟蹤的干擾)之間的不確定性模型:
原始估計中的每個狀態變量更新到新的狀態后,仍然服從高斯分布。我們可以說 的每個狀態變量移動到了一個新的服從高斯分布的區域,協方差為
的每個狀態變量移動到了一個新的服從高斯分布的區域,協方差為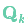 。換句話說就是,我們將這些沒有被跟蹤的干擾當作協方差為
。換句話說就是,我們將這些沒有被跟蹤的干擾當作協方差為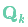 的噪聲來處理。?
的噪聲來處理。?
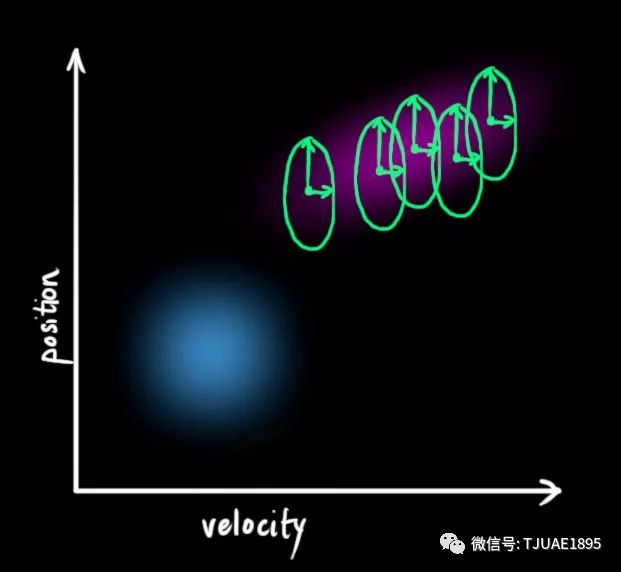
這產生了具有不同協方差(但是具有相同的均值)的新的高斯分布。
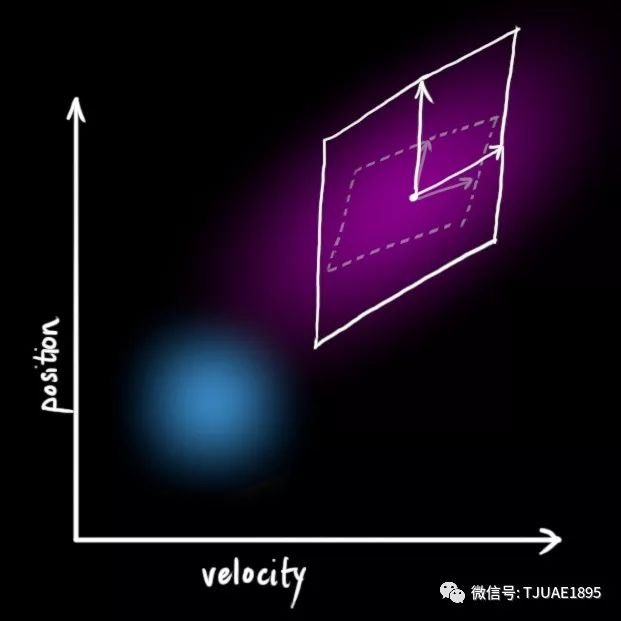
我們通過簡單地添加 得到擴展的協方差,下面給出預測步驟的完整表達式:?
得到擴展的協方差,下面給出預測步驟的完整表達式:?
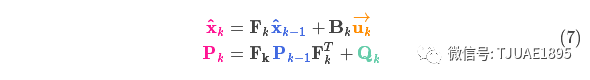
由上式可知,新的最優估計是根據上一最優估計預測得到的,并加上已知外部控制量的修正。
而新的不確定性由上一不確定性預測得到,并加上外部環境的干擾。
好了,我們對系統可能的動向有了一個模糊的估計,用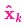 和
和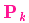 來表示。如果再結合傳感器的數據會怎樣呢?
來表示。如果再結合傳感器的數據會怎樣呢?
用測量值來修正估計值
我們可能會有多個傳感器來測量系統當前的狀態,哪個傳感器具體測量的是哪個狀態變量并不重要,也許一個是測量位置,一個是測量速度,每個傳感器間接地告訴了我們一些狀態信息。
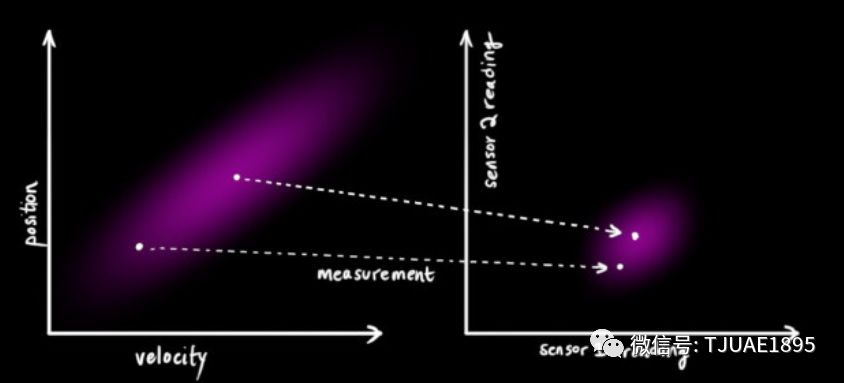
注意,傳感器讀取的數據的單位和尺度有可能與我們要跟蹤的狀態的單位和尺度不一樣,我們用矩陣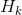 ?來表示傳感器的數據。?
?來表示傳感器的數據。?
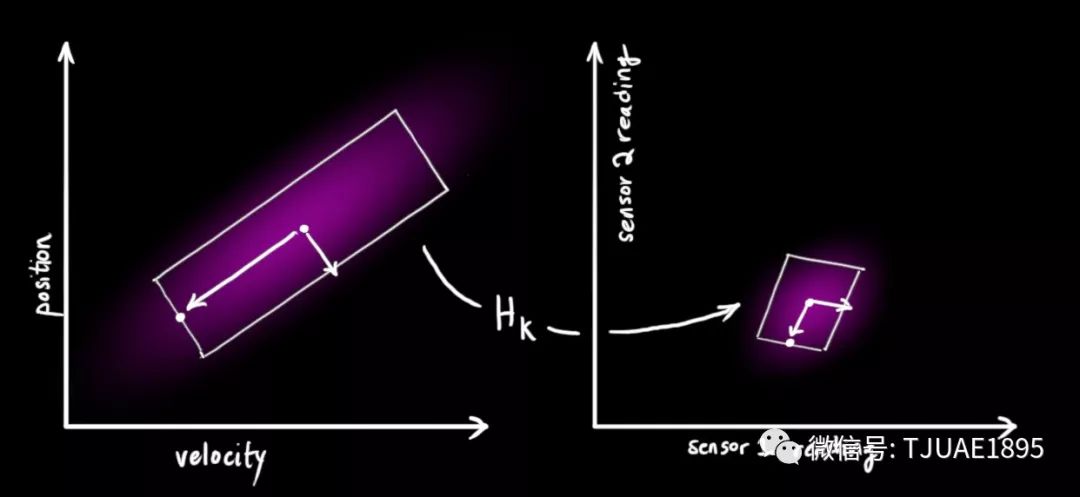
我們可以計算出傳感器讀數的分布,用之前的表示方法如下式所示:
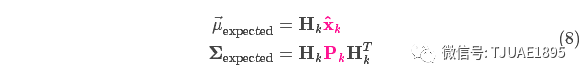
卡爾曼濾波的一大優點就是能處理傳感器噪聲,換句話說,我們的傳感器或多或少都有點不可靠,并且原始估計中的每個狀態可以和一定范圍內的傳感器讀數對應起來。
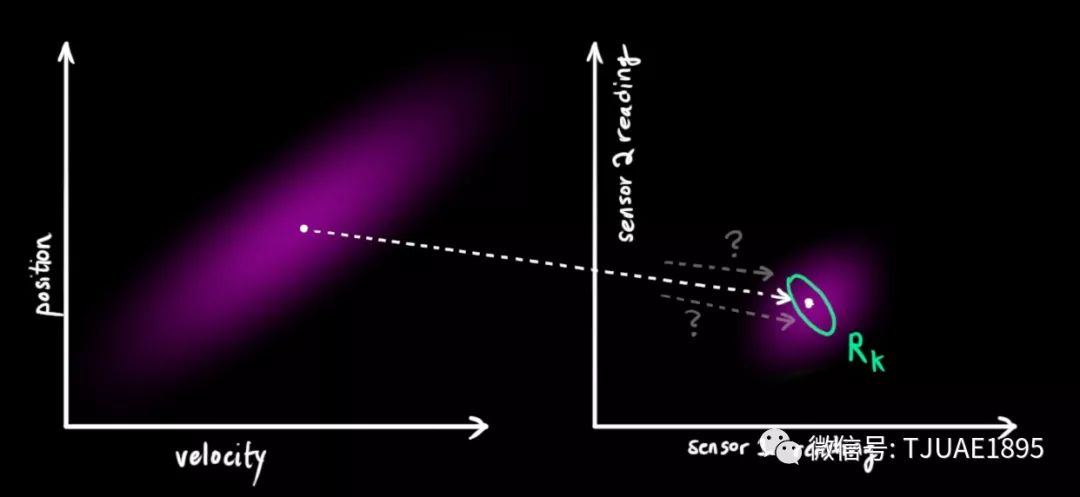
從測量到的傳感器數據中,我們大致能猜到系統當前處于什么狀態。但是由于存在不確定性,某些狀態可能比我們得到的讀數更接近真實狀態。
我們將這種不確定性(例如:傳感器噪聲)用協方差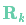 表示,該分布的均值就是我們讀取到的傳感器數據,稱之為
表示,該分布的均值就是我們讀取到的傳感器數據,稱之為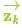 。?
。?
現在我們有了兩個高斯分布,一個是在預測值附近,一個是在傳感器讀數附近。
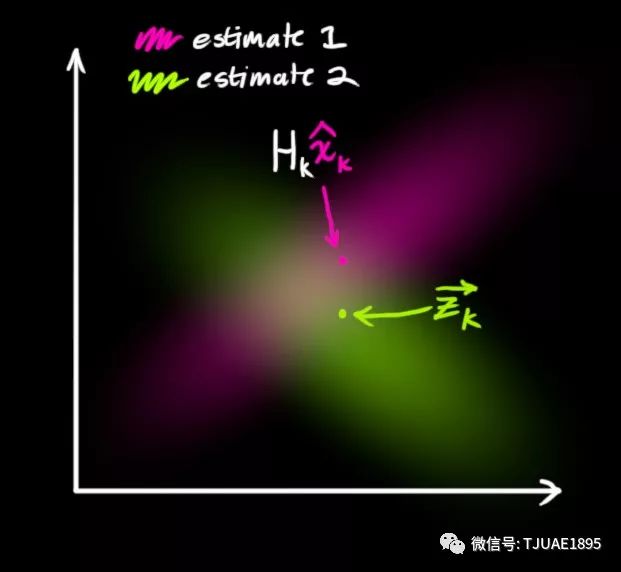
我們必須在預測值(粉紅色)和傳感器測量值(綠色)之間找到最優解。
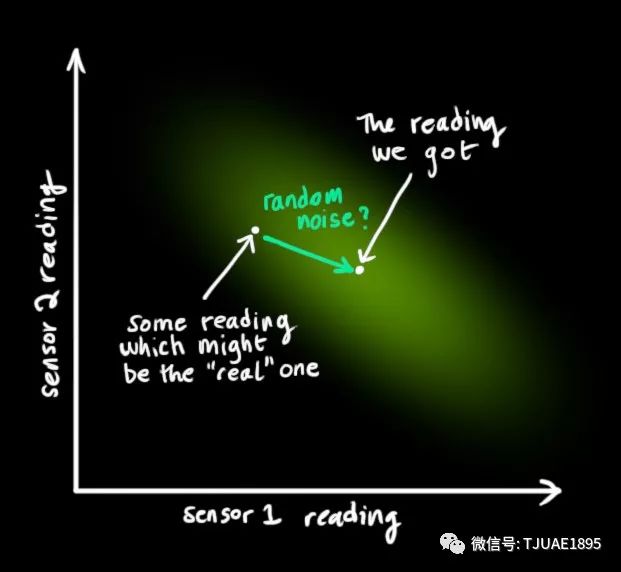
那么,我們最有可能的狀態是什么呢?對于任何可能的讀數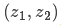 ,有兩種情況:(1)傳感器的測量值;(2)由前一狀態得到的預測值。如果我們想知道這兩種情況都可能發生的概率,將這兩個高斯分布相乘就可以了。?
,有兩種情況:(1)傳感器的測量值;(2)由前一狀態得到的預測值。如果我們想知道這兩種情況都可能發生的概率,將這兩個高斯分布相乘就可以了。?
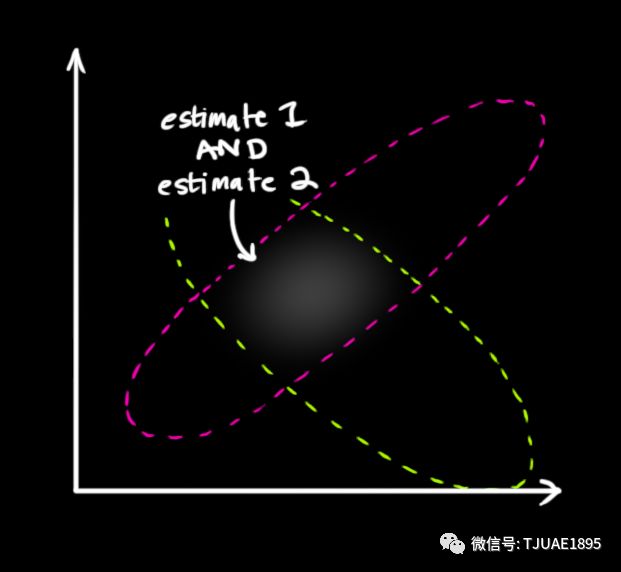
剩下的就是重疊部分了,這個重疊部分的均值就是兩個估計最可能的值,也就是給定的所有信息中的最優估計。
瞧!這個重疊的區域看起來像另一個高斯分布。
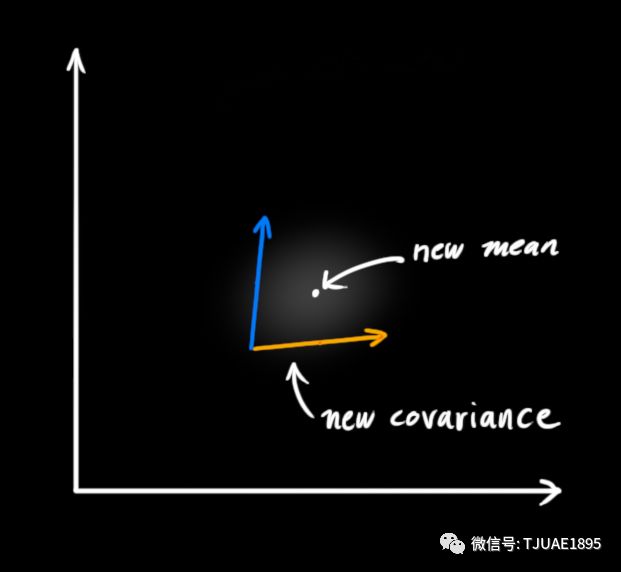
如你所見,把兩個具有不同均值和方差的高斯分布相乘,你會得到一個新的具有獨立均值和方差的高斯分布!下面用公式講解。
融合高斯分布
先以一維高斯分布來分析比較簡單點,具有方差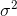 ?和 μ 的高斯曲線可以用下式表示:?
?和 μ 的高斯曲線可以用下式表示:?
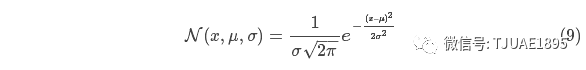
如果把兩個服從高斯分布的函數相乘會得到什么呢?
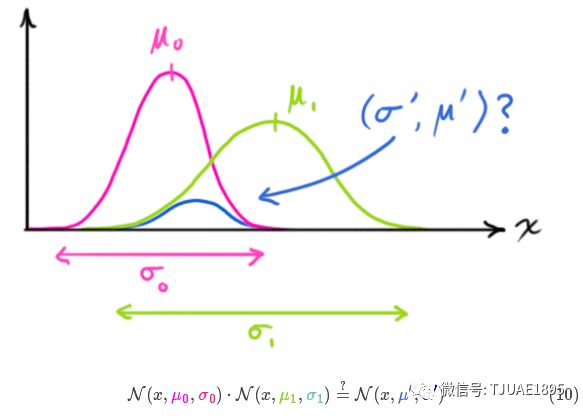
將式(9)代入到式(10)中(注意重新歸一化,使總概率為1)可以得到:
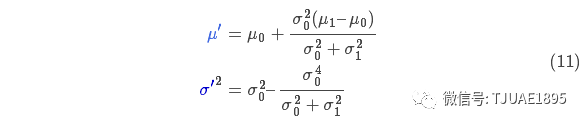
將式(11)中的兩個式子相同的部分用k表示:
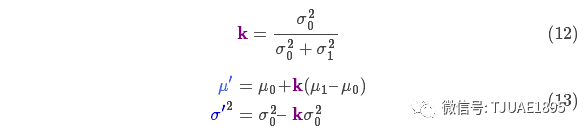
下面進一步將式(12)和(13)寫成矩陣的形式,如果Σ表示高斯分布的協方差,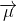 ?表示每個維度的均值,則:?
?表示每個維度的均值,則:?
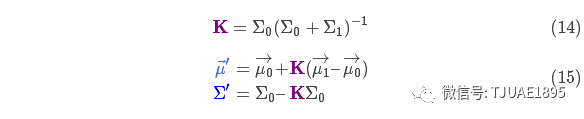
矩陣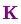 稱為卡爾曼增益,下面將會用到。放松!我們快要完成了!
稱為卡爾曼增益,下面將會用到。放松!我們快要完成了!
將所有公式整合起來
我們有兩個高斯分布,預測部分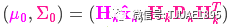 ,和測量部分
,和測量部分 ,將它們放到式(15)中算出它們之間的重疊部分:?
,將它們放到式(15)中算出它們之間的重疊部分:?
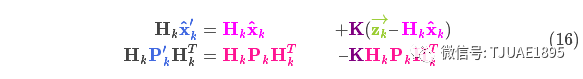
由式(14)可得卡爾曼增益為:
 將式(16)和式(17)的兩邊同時左乘矩陣的逆(注意
將式(16)和式(17)的兩邊同時左乘矩陣的逆(注意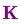 里面包含了?
里面包含了?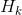 ?)將其約掉,再將式(16)的第二個等式兩邊同時右乘矩陣?
?)將其約掉,再將式(16)的第二個等式兩邊同時右乘矩陣?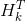 ?的逆得到以下等式:?
?的逆得到以下等式:?
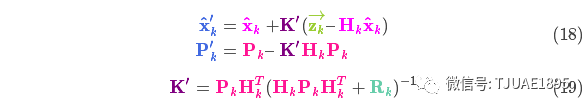
上式給出了完整的更新步驟方程。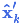 就是新的最優估計,我們可以將它和
就是新的最優估計,我們可以將它和 放到下一個預測和更新方程中不斷迭代。?
放到下一個預測和更新方程中不斷迭代。?
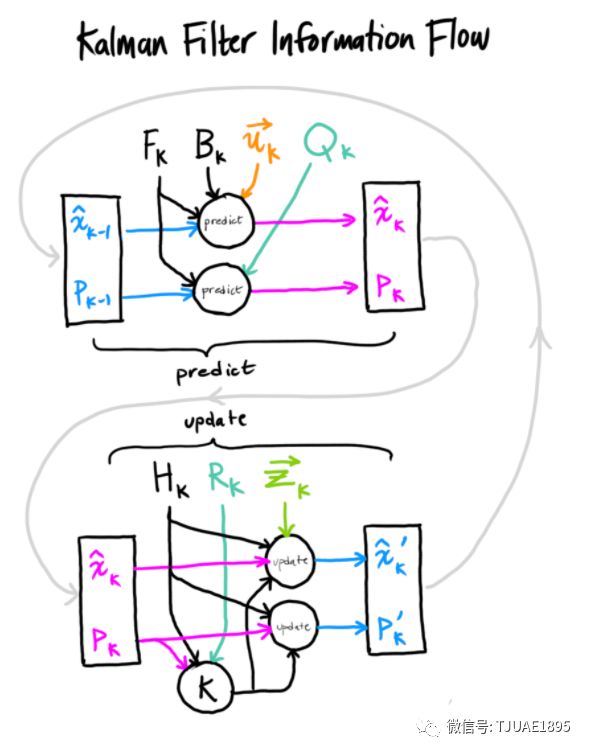
總結
以上所有公式中,你只需要用到式(7)、(18)、(19)。(如果忘了的話,你可以根據式(4)和(15)重新推導一下)
我們可以用這些公式對任何線性系統建立精確的模型,對于非線性系統來說,我們使用擴展卡爾曼濾波,區別在于EKF多了一個把預測和測量部分進行線性化的過程。
-
傳感器
+關注
關注
2552文章
51366瀏覽量
755714 -
機器人
+關注
關注
211文章
28627瀏覽量
207940 -
卡爾曼濾波
+關注
關注
3文章
166瀏覽量
24672
原文標題:卡爾曼濾波算法
文章出處:【微信號:IV_Technology,微信公眾號:智車科技】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 什么是卡爾曼濾波?我們能用卡爾曼濾波做什么?
什么是卡爾曼濾波?我們能用卡爾曼濾波做什么?
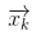
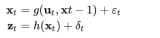










評論