Part1
1、神經網絡基礎問題
(1)BP,Back-propagation(要能推倒)
后向傳播是在求解損失函數L對參數w求導時候用到的方法,目的是通過鏈式法則對參數進行一層一層的求導。這里重點強調:要將參數進行隨機初始化而不是全部置0,否則所有隱層的數值都會與輸入相關,這稱為對稱失效。大致過程是:
首先前向傳導計算出所有節點的激活值和輸出值,
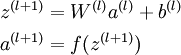
計算整體損失函數:
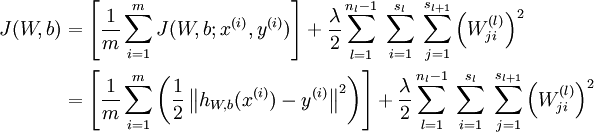
然后針對第L層的每個節點計算出殘差(這里是因為UFLDL中說的是殘差,本質就是整體損失函數對每一層激活值Z的導數),所以要對W求導只要再乘上激活函數對W的導數即可
(2)梯度消失、梯度爆炸
梯度消失:這本質上是由于激活函數的選擇導致的, 最簡單的sigmoid函數為例,在函數的兩端梯度求導結果非常小(飽和區),導致后向傳播過程中由于多次用到激活函數的導數值使得整體的乘積梯度結果變得越來越小,也就出現了梯度消失的現象。
梯度爆炸:同理,出現在激活函數處在激活區,而且權重W過大的情況下。但是梯度爆炸不如梯度消失出現的機會多。(3)常用的激活函數
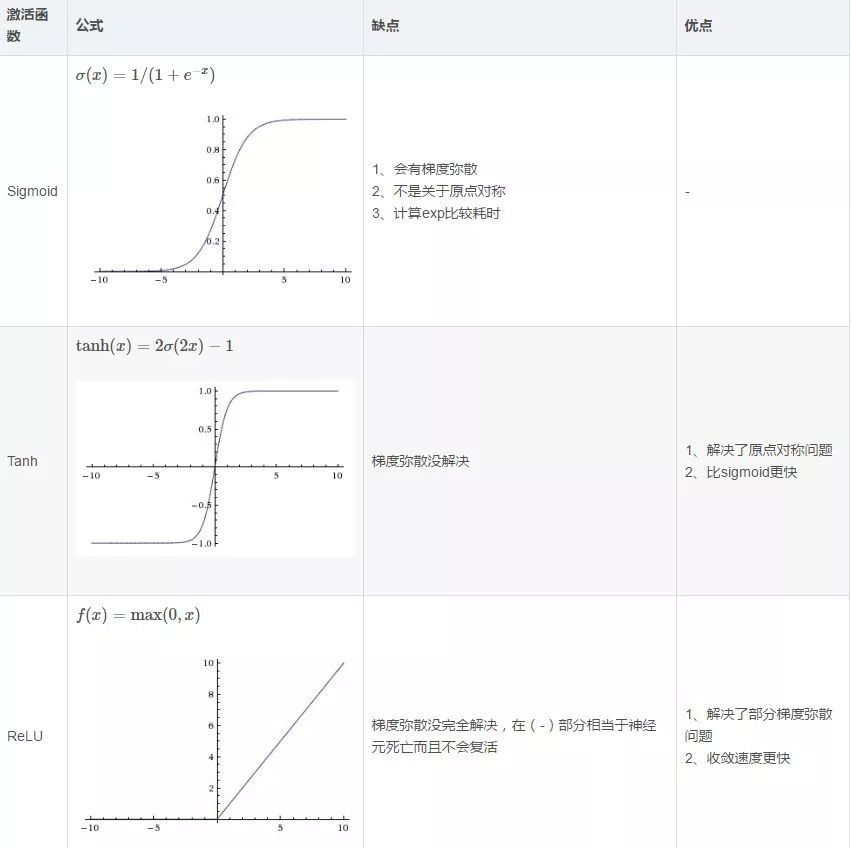
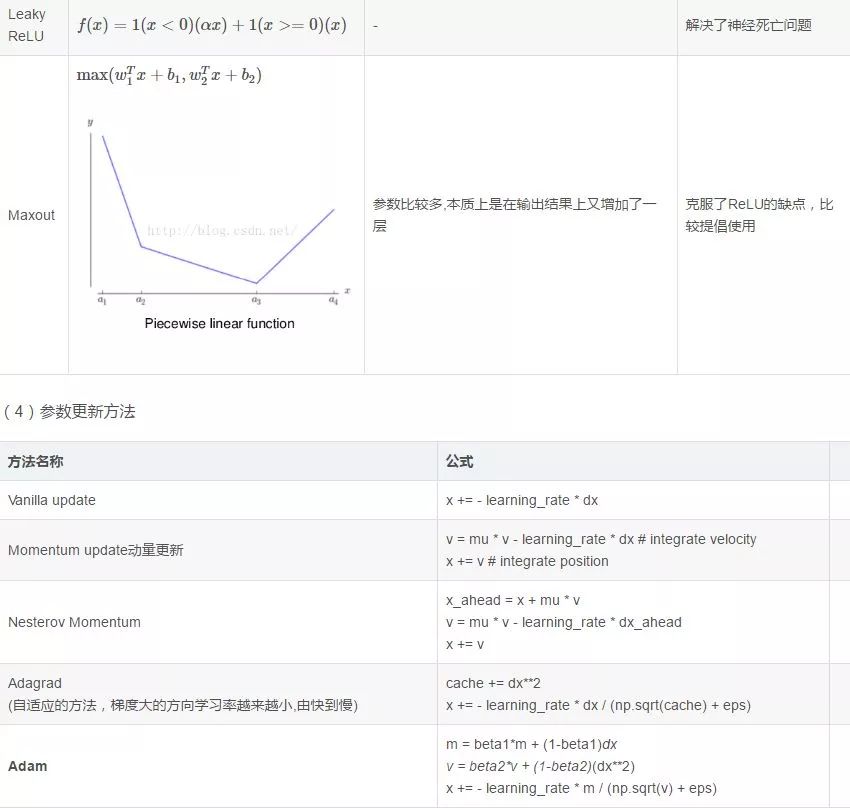
(5)解決overfitting的方法
dropout, regularization, batch normalizatin,但是要注意dropout只在訓練的時候用,讓一部分神經元隨機失活。Batch normalization是為了讓輸出都是單位高斯激活,方法是在連接和激活函數之間加入BatchNorm層,計算每個特征的均值和方差進行規則化。
2、CNN問題
(1) 思想
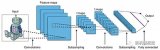
改變全連接為局部連接,這是由于圖片的特殊性造成的(圖像的一部分的統計特性與其他部分是一樣的),通過局部連接和參數共享大范圍的減少參數值。可以通過使用多個filter來提取圖片的不同特征(多卷積核)。
(2)filter尺寸的選擇
通常尺寸多為奇數(1,3,5,7)
(3)輸出尺寸計算公式
輸出尺寸=(N - F +padding*2)/stride + 1
步長可以自由選擇通過補零的方式來實現連接。
(4)pooling池化的作用
雖然通過.卷積的方式可以大范圍的減少輸出尺寸(特征數),但是依然很難計算而且很容易過擬合,所以依然利用圖片的靜態特性通過池化的方式進一步減少尺寸。
(5)常用模型,這個最好能記住模型大致的尺寸參數。

3、RNN
1、RNN原理:
在普通的全連接網絡或CNN中,每層神經元的信號只能向上一層傳播,樣本的處理在各個時刻獨立,因此又被成為前向神經網絡(Feed-forward+Neural+Networks)。而在RNN中,神經元的輸出可以在下一個時間戳直接作用到自身,即第i層神經元在m時刻的輸入,除了(i-1)層神經元在該時刻的輸出外,還包括其自身在(m-1)時刻的輸出。所以叫循環神經網絡
2、RNN、LSTM、GRU區別
RNN引入了循環的概念,但是在實際過程中卻出現了初始信息隨時間消失的問題,即長期依賴(Long-Term Dependencies)問題,所以引入了LSTM。
LSTM:因為LSTM有進有出且當前的cell informaton是通過input gate控制之后疊加的,RNN是疊乘,因此LSTM可以防止梯度消失或者爆炸。推導forget gate,input gate,cell state, hidden information等因為LSTM有進有出且當前的cell informaton是通過input gate控制之后疊加的,RNN是疊乘,因此LSTM可以防止梯度消失或者爆炸的變化是關鍵,下圖非常明確適合記憶:
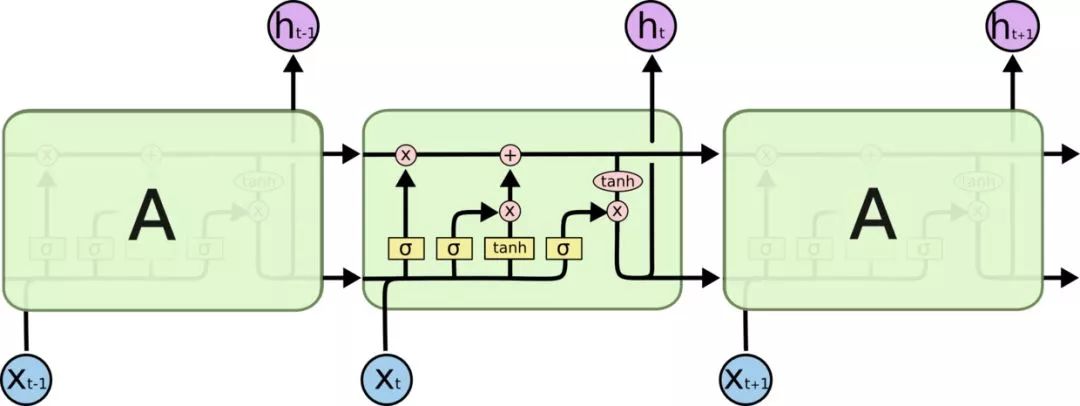
GRU是LSTM的變體,將忘記門和輸入們合成了一個單一的更新門。
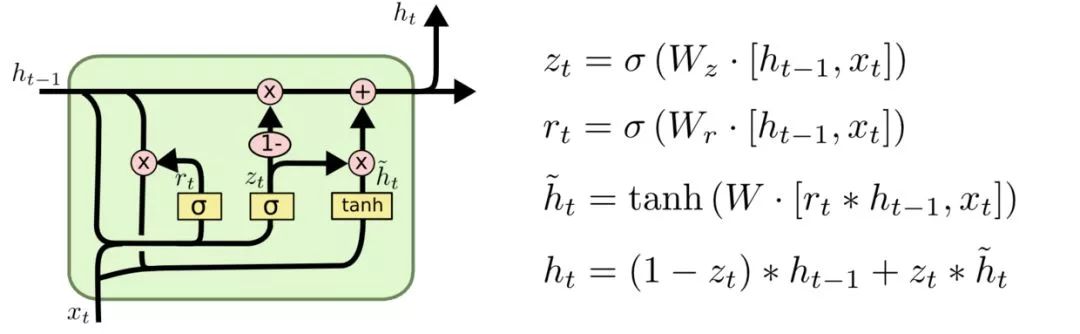
3、LSTM防止梯度彌散和爆炸
LSTM用加和的方式取代了乘積,使得很難出現梯度彌散。但是相應的更大的幾率會出現梯度爆炸,但是可以通過給梯度加門限解決這一問題。
4、引出word2vec
這個也就是Word Embedding,是一種高效的從原始語料中學習字詞空間向量的預測模型。分為CBOW(Continous Bag of Words)和Skip-Gram兩種形式。其中CBOW是從原始語句推測目標詞匯,而Skip-Gram相反。CBOW可以用于小語料庫,Skip-Gram用于大語料庫。具體的就不是很會了。
3、GAN
1、GAN的思想
GAN結合了生成模型和判別模型,相當于矛與盾的撞擊。生成模型負責生成最好的數據騙過判別模型,而判別模型負責識別出哪些是真的哪些是生成模型生成的。但是這些只是在了解了GAN之后才體會到的,但是為什么這樣會有效呢?
假設我們有分布Pdata(x),我們希望能建立一個生成模型來模擬真實的數據分布,假設生成模型為Pg(x;θθ),我們的目的是求解θ的值,通常我們都是用最大似然估計。但是現在的問題是由于我們相用NN來模擬Pdata(x),但是我們很難求解似然函數,因為我們沒辦法寫出生成模型的具體表達形式,于是才有了GAN,也就是用判別模型來代替求解最大似然的過程。
在最理想的狀態下,G可以生成足以“以假亂真”的圖片G(z)。對于D來說,它難以判定G生成的圖片究竟是不是真實的,因此D(G(z)) = 0.5。這樣我們的目的就達成了:我們得到了一個生成式的模型G,它可以用來生成圖片。
2、GAN的表達式
通過分析GAN的表達可以看出本質上就是一個minmax問題。其中V(D, G)可以看成是生成模型和判別模型的差異,而minmaxD說的是最大的差異越小越好。這種度量差異的方式實際上叫做Jensen-Shannon divergence。
3、GAN的實際計算方法
因為我們不可能有Pdata(x)的分布,所以我們實際中都是用采樣的方式來計算差異(也就是積分變求和)。具體實現過程如下:
有幾個關鍵點:判別方程訓練K次,而生成模型只需要每次迭代訓練一次,先最大化(梯度上升)再最小化(梯度下降)。
但是實際計算時V的后面一項在D(x)很小的情況下由于log函數的原因會導致更新很慢,所以實際中通常將后一項的log(1-D(x))變為-logD(x)。
實際計算的時候還發現不論生成器設計的多好,判別器總是能判斷出真假,也就是loss幾乎都是0,這可能是因為抽樣造成的,生成數據與真實數據的交集過小,無論生成模型多好,判別模型也能分辨出來。解決方法有兩個:1、用WGAN 2、引入隨時間減少的噪聲
4、對GAN有一些改進有引入f-divergence,取代Jensen-Shannon divergence,還有很多,這里主要介紹WGAN
5、WGAN
上面說過了用f-divergence來衡量兩個分布的差異,而WGAN的思路是使用Earth Mover distance (挖掘機距離 Wasserstein distance)。
Part
2
1、決策樹樹相關問題
(1)各種熵的計算熵、聯合熵、條件熵、交叉熵、KL散度(相對熵)
熵用于衡量不確定性,所以均分的時候熵最大
KL散度用于度量兩個分布的不相似性,KL(p||q)等于交叉熵H(p,q)-熵H(p)。交叉熵可以看成是用q編碼P所需的bit數,減去p本身需要的bit數,KL散度相當于用q編碼p需要的額外bits。
交互信息Mutual information :I(x,y) = H(x)-H(x|y) = H(y)-H(y|x) 表示觀察到x后,y的熵會減少多少。
(2)常用的樹搭建方法:ID3、C4.5、CART
上述幾種樹分別利用信息增益、信息增益率、Gini指數作為數據分割標準。其中信息增益衡量按照某個特征分割前后熵的減少程度,其實就是上面說的交互信息。用上述信息增益會出現優先選擇具有較多屬性的特征,畢竟分的越細的屬性確定性越高。所以提出了信息增益率的概念,讓含有較多屬性的特征的作用降低。CART樹在分類過程中使用的基尼指數Gini,只能用于切分二叉樹,而且和ID3、C4.5樹不同,Cart樹不會在每一個步驟刪除所用特征。
(3)防止過擬合:剪枝
剪枝分為前剪枝和后剪枝,前剪枝本質就是早停止,后剪枝通常是通過衡量剪枝后損失函數變化來決定是否剪枝。后剪枝有:錯誤率降低剪枝、悲觀剪枝、代價復雜度剪枝
(4)前剪枝的停止條件
節點中樣本為同一類
特征不足返回多類
如果某個分支沒有值則返回父節點中的多類
樣本個數小于閾值返回多類
2、邏輯回歸相關問題
(1)公式推導一定要會
(2)邏輯回歸的基本概念這個最好從廣義線性模型的角度分析,邏輯回歸是假設y服從Bernoulli分布。
(3)L1-norm和L2-norm
其實稀疏的根本還是在于L0-norm也就是直接統計參數不為0的個數作為規則項,但實際上卻不好執行于是引入了L1-norm;而L1norm本質上是假設參數先驗是服從Laplace分布的,而L2-norm是假設參數先驗為Gaussian分布,我們在網上看到的通常用圖像來解答這個問題的原理就在這。但是L1-norm的求解比較困難,可以用坐標軸下降法或是最小角回歸法求解。
(4)LR和SVM對比
首先,LR和SVM最大的區別在于損失函數的選擇,LR的損失函數為Log損失(或者說是邏輯損失都可以)、而SVM的損失函數為hinge loss。
其次,兩者都是線性模型。
最后,SVM只考慮支持向量(也就是和分類相關的少數點)
(5)LR和隨機森林區別
隨機森林等樹算法都是非線性的,而LR是線性的。LR更側重全局優化,而樹模型主要是局部的優化。
(6)常用的優化方法
邏輯回歸本身是可以用公式求解的,但是因為需要求逆的復雜度太高,所以才引入了梯度下降算法。
一階方法:梯度下降、隨機梯度下降、mini 隨機梯度下降降法。隨機梯度下降不但速度上比原始梯度下降要快,局部最優化問題時可以一定程度上抑制局部最優解的發生。
二階方法:牛頓法、擬牛頓法。這里詳細說一下牛頓法的基本原理和牛頓法的應用方式。牛頓法其實就是通過切線與x軸的交點不斷更新切線的位置,直到達到曲線與x軸的交點得到方程解。在實際應用中我們因為常常要求解凸優化問題,也就是要求解函數一階導數為0的位置,而牛頓法恰好可以給這種問題提供解決方法。實際應用中牛頓法首先選擇一個點作為起始點,并進行一次二階泰勒展開得到導數為0的點進行一個更新,直到達到要求,這時牛頓法也就成了二階求解問題,比一階方法更快。我們常常看到的x通常為一個多維向量,這也就引出了Hessian矩陣的概念(就是x的二階導數矩陣)。缺點:牛頓法是定長迭代,沒有步長因子,所以不能保證函數值穩定的下降,嚴重時甚至會失敗。還有就是牛頓法要求函數一定是二階可導的。而且計算Hessian矩陣的逆復雜度很大。擬牛頓法: 不用二階偏導而是構造出Hessian矩陣的近似正定對稱矩陣的方法稱為擬牛頓法。擬牛頓法的思路就是用一個特別的表達形式來模擬Hessian矩陣或者是他的逆使得表達式滿足擬牛頓條件。主要有DFP法(逼近Hession的逆)、BFGS(直接逼近Hession矩陣)、 L-BFGS(可以減少BFGS所需的存儲空間)。
3、SVM相關問題
(1)帶核的SVM為什么能分類非線性問題?
核函數的本質是兩個函數的內積,而這個函數在SVM中可以表示成對于輸入值的高維映射。注意核并不是直接對應映射,核只不過是一個內積
(2)RBF核一定是線性可分的嗎不一定,RBF核比較難調參而且容易出現維度災難,要知道無窮維的概念是從泰勒展開得出的。
(3)常用核函數及核函數的條件:核函數選擇的時候應該從線性核開始,而且在特征很多的情況下沒有必要選擇高斯核,應該從簡單到難的選擇模型。我們通常說的核函數指的是正定和函數,其充要條件是對于任意的x屬于X,要求K對應的Gram矩陣要是半正定矩陣。
RBF核徑向基,這類函數取值依賴于特定點間的距離,所以拉普拉斯核其實也是徑向基核。
線性核:主要用于線性可分的情況
多項式核
(4)SVM的基本思想
間隔最大化來得到最優分離超平面。方法是將這個問題形式化為一個凸二次規劃問題,還可以等價位一個正則化的合頁損失最小化問題。SVM又有硬間隔最大化和軟間隔SVM兩種。這時首先要考慮的是如何定義間隔,這就引出了函數間隔和幾何間隔的概念(這里只說思路),我們選擇了幾何間隔作為距離評定標準(為什么要這樣,怎么求出來的要知道),我們希望能夠最大化與超平面之間的幾何間隔x,同時要求所有點都大于這個值,通過一些變化就得到了我們常見的SVM表達式。接著我們發現定義出的x只是由個別幾個支持向量決定的。對于原始問題(primal problem)而言,可以利用凸函數的函數包來進行求解,但是發現如果用對偶問題(dual )求解會變得更簡單,而且可以引入核函數。而原始問題轉為對偶問題需要滿足KKT條件(這個條件應該細細思考一下)到這里還都是比較好求解的。因為我們前面說過可以變成軟間隔問題,引入了懲罰系數,這樣還可以引出hinge損失的等價形式(這樣可以用梯度下降的思想求解SVM了)。我個人認為難的地方在于求解參數的SMO算法。
(5)是否所有的優化問題都可以轉化為對偶問題
這個問題我感覺非常好,有了強對偶和弱對偶的概念。用知乎大神的解釋吧
(6)處理數據偏斜
可以對數量多的類使得懲罰系數C越小表示越不重視,相反另數量少的類懲罰系數變大。
4、Boosting和Bagging
(1)隨機森林
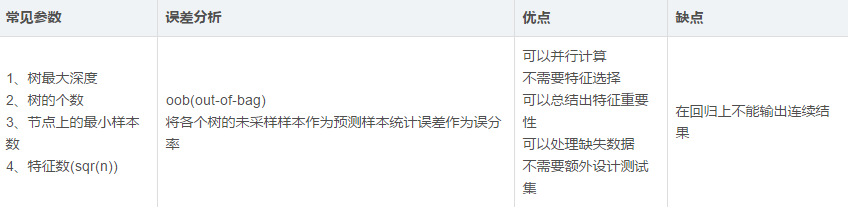
隨機森林改變了決策樹容易過擬合的問題,這主要是由兩個操作所優化的:1、Boostrap從袋內有放回的抽取樣本值2、每次隨機抽取一定數量的特征(通常為sqr(n))。
分類問題:采用Bagging投票的方式選擇類別頻次最高的
回歸問題:直接取每顆樹結果的平均值。
(2)Boosting之AdaBoost
Boosting的本質實際上是一個加法模型,通過改變訓練樣本權重學習多個分類器并進行一些線性組合。而Adaboost就是加法模型+指數損失函數+前項分布算法。Adaboost就是從弱分類器出發反復訓練,在其中不斷調整數據權重或者是概率分布,同時提高前一輪被弱分類器誤分的樣本的權值。最后用分類器進行投票表決(但是分類器的重要性不同)。
(3)Boosting之GBDT
將基分類器變成二叉樹,回歸用二叉回歸樹,分類用二叉分類樹。和上面的Adaboost相比,回歸樹的損失函數為平方損失,同樣可以用指數損失函數定義分類問題。但是對于一般損失函數怎么計算呢?GBDT(梯度提升決策樹)是為了解決一般損失函數的優化問題,方法是用損失函數的負梯度在當前模型的值來模擬回歸問題中殘差的近似值。 (注:由于GBDT很容易出現過擬合的問題,所以推薦的GBDT深度不要超過6,而隨機森林可以在15以上。)
(4)GBDT和Random Forest區別這個就和上面說的差不多。
(5)Xgboost這個工具主要有以下幾個特點:
支持線性分類器
可以自定義損失函數,并且可以用二階偏導
加入了正則化項:葉節點數、每個葉節點輸出score的L2-norm
支持特征抽樣
在一定情況下支持并行,只有在建樹的階段才會用到,每個節點可以并行的尋找分裂特征。
5、KNN和Kmean
(1)KNN 和Kmean缺點都屬于惰性學習機制,需要大量的計算距離過程,速度慢的可以(但是都有相應的優化方法)。
(2)KNNKNN不需要進行訓練,只要對于一個陌生的點利用離其最近的K個點的標簽判斷其結果。KNN相當于多數表決,也就等價于經驗最小化。而KNN的優化方式就是用Kd樹來實現。
(3)Kmean要求自定義K個聚類中心,然后人為的初始化聚類中心,通過不斷增加新點變換中心位置得到最終結果。Kmean的缺點可以用Kmean++方法進行一些解決(思想是使得初始聚類中心之間的距離最大化)
6、EM算法、HMM、CRF
這三個放在一起不是很恰當,但是有互相有關聯,所以就放在這里一起說了。注意重點關注算法的思想。(1)EM算法EM算法是用于含有隱變量模型的極大似然估計或者極大后驗估計,有兩步組成:E步,求期望(expectation);M步,求極大(maxmization)。本質上EM算法還是一個迭代算法,通過不斷用上一代參數對隱變量的估計來對當前變量進行計算,直到收斂。 (注意:EM算法是對初值敏感的,而且EM是不斷求解下界的極大化逼近求解對數似然函數的極大化的算法,也就是說EM算法不能保證找到全局最優值。對于EM的導出方法也應該掌握。 )
(2)HMM算法隱馬爾可夫模型是用于標注問題的生成模型。有幾個參數(ππ,A,B):初始狀態概率向量π,狀態轉移矩陣A,觀測概率矩陣B。稱為馬爾科夫模型的三要素。馬爾科夫三個基本問題:
概率計算問題:給定模型和觀測序列,計算模型下觀測序列輸出的概率。–》前向后向算法
學習問題:已知觀測序列,估計模型參數,即用極大似然估計來估計參數。–》Baum-Welch(也就是EM算法)和極大似然估計。
預測問題:已知模型和觀測序列,求解對應的狀態序列。–》近似算法(貪心算法)和維比特算法(動態規劃求最優路徑)
(3)條件隨機場CRF給定一組輸入隨機變量的條件下另一組輸出隨機變量的條件概率分布密度。條件隨機場假設輸出變量構成馬爾科夫隨機場,而我們平時看到的大多是線性鏈條隨機場,也就是由輸入對輸出進行預測的判別模型。求解方法為極大似然估計或正則化的極大似然估計。
之所以總把HMM和CRF進行比較,主要是因為CRF和HMM都利用了圖的知識,但是CRF利用的是馬爾科夫隨機場(無向圖),而HMM的基礎是貝葉斯網絡(有向圖)。而且CRF也有:概率計算問題、學習問題和預測問題。大致計算方法和HMM類似,只不過不需要EM算法進行學習問題。
(4)HMM和CRF對比其根本還是在于基本的理念不同,一個是生成模型,一個是判別模型,這也就導致了求解方式的不同。
7、常見基礎問題
(1)數據歸一化(或者標準化,注意歸一化和標準化不同)的原因
要強調:能不歸一化最好不歸一化,之所以進行數據歸一化是因為各維度的量綱不相同。而且需要看情況進行歸一化。
有些模型在各維度進行了不均勻的伸縮后,最優解與原來不等價(如SVM)需要歸一化。
有些模型伸縮有與原來等價,如:LR則不用歸一化,但是實際中往往通過迭代求解模型參數,如果目標函數太扁(想象一下很扁的高斯模型)迭代算法會發生不收斂的情況,所以最壞進行數據歸一化。
補充:其實本質是由于loss函數不同造成的,SVM用了歐拉距離,如果一個特征很大就會把其他的維度dominated。而LR可以通過權重調整使得損失函數不變。
(2)衡量分類器的好壞:這里首先要知道TP、FN(真的判成假的)、FP(假的判成真)、TN四種(可以畫一個表格)。幾種常用的指標:
精度precision = TP/(TP+FP) = TP/~P (~p為預測為真的數量)
召回率 recall = TP/(TP+FN) = TP/ P
F1值: 2/F1 = 1/recall + 1/precision
ROC曲線:ROC空間是一個以偽陽性率(FPR,false positive rate)為X軸,真陽性率(TPR, true positive rate)為Y軸的二維坐標系所代表的平面。其中真陽率TPR = TP / P = recall, 偽陽率FPR = FP / N
(3)SVD和PCA
PCA的理念是使得數據投影后的方差最大,找到這樣一個投影向量,滿足方差最大的條件即可。而經過了去除均值的操作之后,就可以用SVD分解來求解這樣一個投影向量,選擇特征值最大的方向。
(4)防止過擬合的方法
過擬合的原因是算法的學習能力過強;一些假設條件(如樣本獨立同分布)可能是不成立的;訓練樣本過少不能對整個空間進行分布估計。處理方法:
早停止:如在訓練中多次迭代后發現模型性能沒有顯著提高就停止訓練
數據集擴增:原有數據增加、原有數據加隨機噪聲、重采樣
正則化
交叉驗證
特征選擇/特征降維
(5)數據不平衡問題這主要是由于數據分布不平衡造成的。解決方法如下:
采樣,對小樣本加噪聲采樣,對大樣本進行下采樣
進行特殊的加權,如在Adaboost中或者SVM中
采用對不平衡數據集不敏感的算法
改變評價標準:用AUC/ROC來進行評價
采用Bagging/Boosting/ensemble等方法
考慮數據的先驗分布
-
神經網絡
+關注
關注
42文章
4779瀏覽量
101044 -
機器學習
+關注
關注
66文章
8438瀏覽量
132927 -
深度學習
+關注
關注
73文章
5512瀏覽量
121410
原文標題:收藏!機器學習與深度學習面試問題總結
文章出處:【微信號:machinelearningai,微信公眾號:機器學習算法與人工智能】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 機器學習與深度學習問題總結
機器學習與深度學習問題總結











評論