不管你怎樣看待數據科學家的研究工作，都不能輕易忽略對數據進行分析、組織和梳理的重要性。Glassdoor 網站收集了大量的雇主和員工的反饋數據，發現數據科學家位列 "美國最好的 25 個職位"榜首。盡管摘得這一桂冠，但需要數據科學家們研究的工作內容還在不斷新增。隨著機器學習等技術越來越普遍的應用，深度學習等熱門領域受到研究人員和工程師以及企業的關注日漸增加，數據科學家必將繼續站在技術創新的浪潮之巔，引領著時代的技術變革。

因此他們需要系統地研究統計機器學習，該學科脫胎于統計學和泛函分析，并結合了信息論、最優化理論和線性代數等多門學科。盡管強大的編程能力對數據科學家而言十分重要，但數據科學家也不完全就是軟件工程師。事實上熟練掌握Python對于他們就已足夠，真正重要的是同時具備編程、統計和批判思維的能力。

正如Josh Wills所言：“數據科學家比程序員擅長統計學，比統計學家擅長編程。” 很多軟件工程師想轉型數據科學家，但他們盲目地使用 TensorFlow 或 Apache Spark 等機器學習框架來處理數據，卻忽略了背后的統計學理論知識。也就是統計學習理論，機器學習的理論框架，這些都源自統計學和泛函分析。

那么為什么要學習統計學習？我們只有深刻理解了不同技術背后的想法，才能學以致用。也只有先易后難，才能游刃有余、融會貫通。同時，準確評估一種方法的性能也非常重要，不僅能知道工作效果的好壞，也能得知方法的適用范圍。此外，統計學習也是一個令人振奮的研究領域，在科學、工業和金融領域都有重要的應用。最后，統計學習是培養現代數據科學家的基礎要素。統計學習問題應用的例子如下：

確定前列腺癌的風險因素

根據對數周期圖對錄音進行分類

根據人口統計學、飲食和臨床測量預測是否會患有心臟病

定制垃圾郵件檢測系統

識別手寫郵政編碼

對組織樣本進行癌癥分類

建立人口調查數據中的薪資與人口統計變量的關系

在介紹常用的10種統計技術之前，我們需要先區分一下機器學習和統計學習，主要有以下幾點區別：

機器學習是人工智能的一個分支

統計學習是統計領域的一個分支

機器學習更側重于大規模應用和預測的精準性

統計學習強調模型及其解釋性、精度和不確定性

但區別也在變得越來越模糊，兩者很多時候交織在一起

不得不說，市場營銷把機器學習炒得很熱

線性回歸

在統計學中，線性回歸是一種通過擬合因變量和自變量之間的最佳線性關系來預測目標變量的方法。最佳擬合即表示由當前的線性表達式得到的預測輸出與實際觀測值的誤差和最小。

線性回歸主要分為簡單線性回歸和多元線性回歸。簡單線性回歸使用一個自變量來擬合最佳線性關系預測因變量；而多元線性回歸使用多個自變量來擬合最佳線性關系預測因變量。

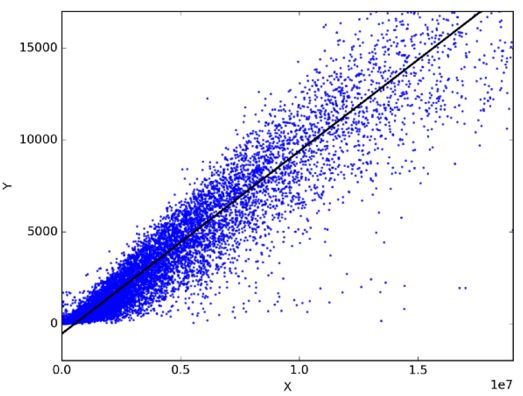
那么線性回歸可以用在哪些實際問題上呢？實際上任意選擇日常生活中相關的兩件事，你便能通過線性回歸模型得到他們之間的線性關系。比如你有了過去三年的月消費、月收入和月旅行次數的數據，那你可以預測下一年月支出，還可以知道是月收入還是月旅行次數對月消費更影響，甚至還能用方程式表達月收入、月旅行次數、月消費三者之間的關系呢。

分類

分類是屬于一種數據挖掘技術，將數據集分成多個類別可以幫助更準確的預測和分析。分類是一種高效分析大型數據集的方法，典型的代表有邏輯回歸(Logistic Regression) 分析和判別分析(Discriminant Analysis）。

邏輯回歸分析適合用于因變量為二元類別時的回歸分析。 和所有回歸分析一樣，邏輯回歸也屬于預測分析。 Logistic回歸用于描述數據，并解釋二元因變量與一個或多個名義、序數、區間或比率級別等描述性的自變量之間的關系。 適合邏輯回歸的問題類型有：

體重每超出標準體重一磅或每天每抽一包煙對得肺癌概率是否有影響（是或否）。

卡路里攝入、脂肪攝入和年齡對心臟病是否有影響（是或否）。

在判別分析中，兩個或多個已知的集合、簇或群體都可以作為分類的先驗知識，使用時根據被測特征就可把新的觀測值劃分到相應類別。判別分析會對每個類中的預測因素 X 分別進行建模，然后根據貝葉斯定理便能將其轉換成只需根據 X 值就可獲得對應類別的概率估計。此類模型既可以是線性判別分析，也可以是二次判別分析。

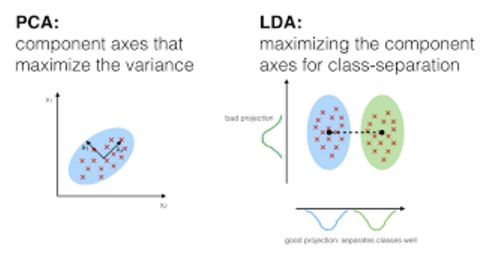
Linear Discriminant Analysis線性判別分析，通過自變量的線性組合對每個觀測值計算“判別分數”，并對其所處的響應變量Y類別進行分類。它假設每個類別內的觀測值都服從多變量高斯分布，且每個類別的方差一樣。

Quadratic Discriminant Analysis二次判別分析，提供了另一種方法。與LDA一樣，QDA也假設來自Y的每類觀察值都服從高斯分布。但與LDA不同的是，QDA假定每個類別都有其自己的協方差矩陣，也就是說每個類別的方差不一樣。

重采樣方法

重采樣方法就是從原始數據樣本中重復提取樣本，屬于統計推斷的非參數方法。重采樣不使用通用分布表來逼近地計算概率 p 的值，而是基于實際數據生成一個獨特的采樣分布。這種采用分布通過經驗性方法生成，而不是分析方法，它能夠基于數據所有可能結果的無偏樣本獲取無偏估計。為了很好的理解重采樣的概念，我們需要先了解Bootstrapping和交叉驗證（Cross-Validation）：

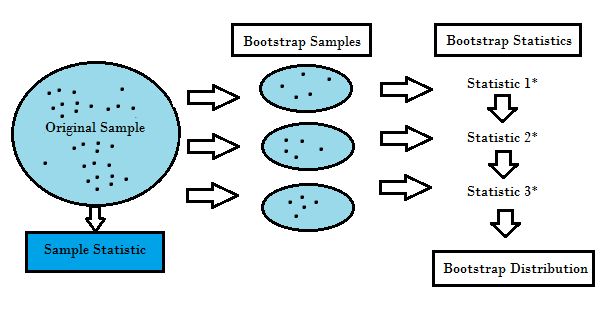
Bootstrapping是有助于在許多情況下驗證預測模型的性能和集成方法，估計模型的偏差和方差。 它通過對原始數據進行有放回的采樣，并將“未被選擇”的數據點作為測試用例。 我們可以多做幾次這樣的操作，然后用平均值來作為我們對模型性能的估計。

Cross validation交叉驗證通過將訓練數據分成k個部分來驗證模型性能，使用k-1部分作為訓練集，余下的部分作為測試集。 重復不同的k次后，將k個分數的平均值作為模型的性能估計。

通常對于線性模型而言，普通的最小二乘法是擬合數據時的主要標準。 接下來的3種方法可以為線性模型擬合提供更好的預測精度和模型可解釋性。

子集選擇

子集選擇的主要目的是挑選出與問題最相關的 p 個預測因子，然后使用該子集特征和最小二乘法擬合模型。

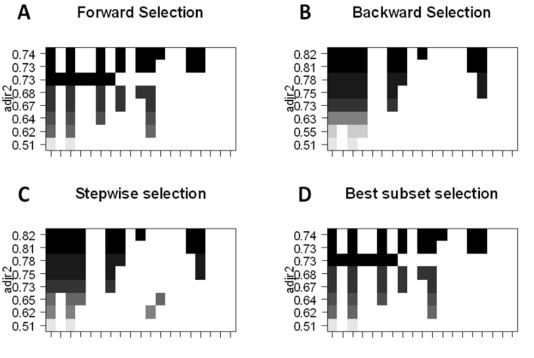
最佳子集的選擇，我們可以為 p 個預測因子的每個組合分別擬合普通最小二乘回歸，然后再觀察各個模型的擬合結果。算法分為兩個階段：（1）擬合包含 k 個預測因子的所有模型，其中 k 表示模型的最大長度；（2）使用交叉驗證預測損失選擇單個模型。要記住，不能單純使用訓練誤差評估模型的擬合情況，驗證集或測試集的誤差也是十分重要的，因為 RSS 和 R^2 會隨變量的增加而單調遞增。最好的方法就是通過選擇測試集中最高的 R^2 和最低的 RSS 來交叉驗證，從而選擇模型。

前向逐步選擇，可以選出 p 個預測因子的較小子集。算法先從不包含預測因子的模型開始，然后逐步地添加預測因子到模型中，直到所有預測因子都包含在模型中。添加預測因子的順序是根據不同變量對模型擬合性能提升的程度來確定的，不斷添加新的預測因子，直到交叉驗證誤差沒有大的改變。

后向逐步選擇，與前向逐步選擇相反，首先模型包含所有 p個 預測因子，然后迭代地移除用處最小的預測因子。

混合法，主體遵循前向逐步方法，但在添加每個新變量之后，該方法可能還會移除對模型擬合無用的變量。

特征縮減技術

特征縮減技術使用了所有 p 個預測因子進行建模，然而，表示預測因子重要性的系數將隨最小二乘誤差向零收縮，這種收縮也稱之為正則化，它旨在減少方差以防止模型的過擬合。常用的縮減系數方法有lasso(L1正則化)，嶺回歸(L2正則化)。

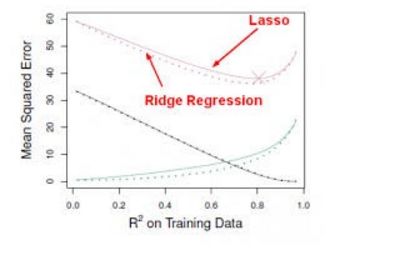
Ridge regression嶺回歸，跟最小二乘法很像都是尋求減少 RSS 的系數估計，只不過它是通過對損失函數(即優化目標)加入懲罰項，使得訓練求解參數過程中會考慮到系數的大小。我們不需要數學分析就能看出 Ridge 回歸很擅長于將特征收縮到最小的子空間中。如主成分分析PCA，通過Ridge 回歸可以將數據投影到低維空間，并在系數空間內收縮較低方差的成分而保留有較高方差的成分。

但Ridge 回歸有一個缺點，最終的模型需要包含所有 p 個預測因子，這源于盡管懲罰項將會令許多預測因子的系數逼近零，但又一定不等于零。雖然這對預測準確度并沒有什么影響，卻令模型的結果更難以解釋。Lasso 方法就很好的克服了這一缺點，因為它能在 s 足夠小的時候迫使一些預測因子的系數歸零。當 s = 1 時，就像正常的OLS 回歸，而當 s 逼近 0 時，系數將收縮到零。因此 Lasso 回歸同樣是執行變量選擇的好方法。

降維（維數減約）

降維是將將p + 1個系數估計問題簡化為為M + 1系數估計問題，其中M

Principal Components Regression主成分回歸，是從大量的變量中尋找低維特征集的方法。數據中的第一主成分（first principal component）是指觀測數據沿著這個變量方向的變化最大，也就是說若用 p 個不同的主成分分別擬合數據，那第一主成分必然是最接近數據分布的那條線。第二主成分是和第一主成分不相關的變量的線性組合，且在該約束下有最大的方差。主要思想是主成分能在各個互相垂直的方向使用數據的線性組合得到最大的方差。基于這種方法，我們還能結合相關變量的效應從數據中獲取更多的信息，畢竟在常規的最小二乘法中需要舍棄其中一個相關變量。

由于PCR 方法需要得到 X 的最優線性組合。由于 X 對應的輸出 Y 對主成分方向的計算沒有影響，也就是說這些組合（方向）是通過無監督方法獲得的，那么就無法保證這些方向是預測器的最優表征，也無法保證能獲得最優預測輸出。偏最小二乘法（PLS）作為 PCR 的代替方法，屬于有監督方法。和 PCR 類似，PLS 也是一種降維方法，它首先提取一個新的較小的特征集合（原始特征的線性組合），然后通過最小二乘法將原來的模型擬合為一個新的具有 M 個特征的線性模型，通過對模型預測誤差來評價特征集合是否是Y的最優線性組合。

非線性模型

在統計學中，非線性回歸屬于回歸分析的一種形式，通過模型參數的非線性組合來（依賴于一個或多個獨立變量）對觀測數據建模，并使用逐次逼近法來擬合數據。以下是幾種處理非線性模型的重要技術:

階梯函數（step function），變量為實數，可以寫成區間的效用函數的有限線性組合的形式。通俗的講，階梯函數就是一種只有有限部分的分段常數函數。

分段函數（piecewise function）通過多個子函數定義，且每一個子函數被定義在確定的區間上。分段實際上是函數的表示方式，而不是函數自身特性，但通過額外的限定條件，它也可以用于描述函數本身。例如，一個分段多項式函數是一個在每一個子定義上為多項式的函數，其中每一個多項式都可能是不同的。

樣條曲線（spline）是一種用多項式分段定義的特殊函數。在計算機圖形學中，樣條曲線是一種分段多項式參數化曲線。由于結構簡單、評估簡易和精度高，以及通過曲線擬合和交互曲線設計就能逼近復雜曲線的能力，使得樣條曲線很常用。

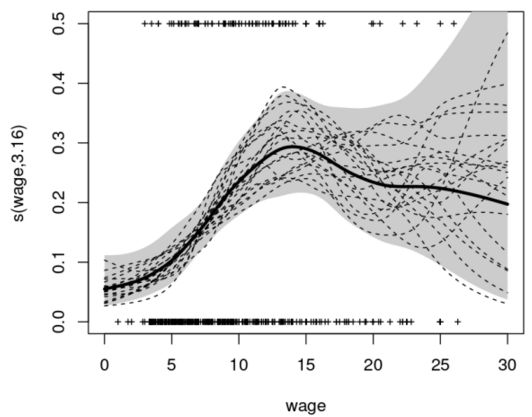
廣義加性模型（generalized additive model）是一種廣義線性模型，其中線性預測器線性依賴于某些預測器變量的未知平滑函數，其主要作用就是推斷這些平滑函數。

基于樹的方法

基于樹的方法可以用于回歸和分類問題，它會將預測器空間分層或分割成一些簡單的區域。由于預測器空間的分裂規則集合可以總結為一個樹，因此也被稱為決策樹方法。以下的方法是幾種不同的樹，它們可以組合起來投票輸出統一的預測。

Bagging能通過從原始數據中生成額外的訓練數據（通過組合和重復生成和原始數據大小相同的多段數據）來減少預測的方差，但無法提高模型的預測能力。

Boosting是一種計算輸出的方法，使用多個不同的模型，然后使用加權平均的方法對結果取平均值。一般結合各方法的優勢來改變這些方法所占的權重，此外，針對更寬泛的輸入數據還可以微調參數得到更佳的預測能力。

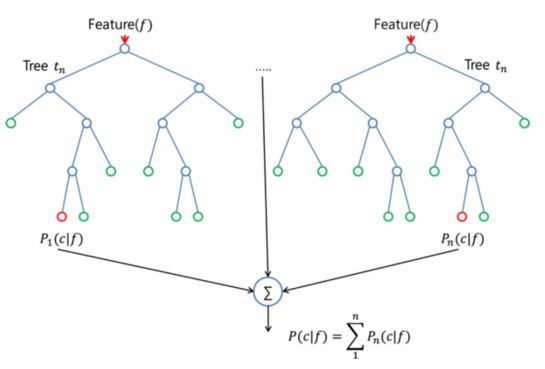
隨機森林算法（random forest algorithm）實際上和 bagging 算法很相似，同樣是對訓練集提取隨機 bootstrap 樣本。然而，除了 bootstrap 樣本以外，還可以提取特征的隨機子集來訓練單個樹；在 bagging 中，則需要為每個樹提供全部的特征。由于特征選擇是隨機的，相比常規的bagging 算法，每個樹之間更加獨立，從而通常能獲得更好的預測性能（得益于更好的方差-偏差權衡）。由于每個樹只需要學習特征的一個子集，因此速度也得以提升。

支持向量機

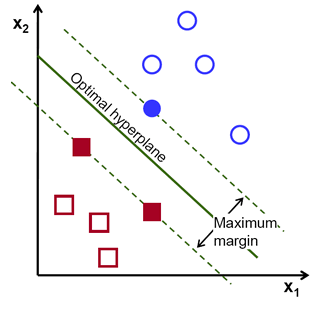
支持向量機（SVM）是一種常用的有監督學習分類技術。通俗地說，它尋找兩類點集的最優超平面（hyperplane，在 2D 空間中是線，在 3D 空間中是面，在高維空間中就是超平面。超平面是n 維空間的 n-1 維子空間）。這個超平面使得兩類點集的間隔最大，本質上是約束最優化問題，在一定約束下使得間隔最大化，從而實現數據的完美分類。

"支持向量"，就是那些支持著超平面的數據點，也可以說是離超平面最近的數據點。在上圖中，藍色填充圓和兩個填充方塊就是支持向量。使用過程中，當兩類數據線性不可分時，數據點可以通過核函數投影到高維空間中，使得數據變得線性可分。而多分類問題也可以分解成多個"一對一"（one-versus-one）或"一對剩余"（one-versus-rest）的二分類問題。

無監督學習

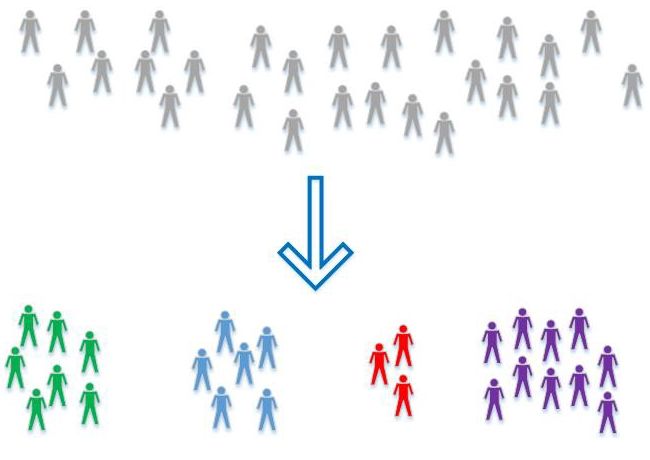
有監督學習是機器學習中的一大部分，其中數據分類已知。當數據分類是未知時，就需要使用另一種技術了，就是無監督學習，它們需要自己去發現數據中的模式。聚類（clustring）是一種典型的無監督學習，數據會根據相關性被分為多簇。以下是幾種最常用的無監督學習算法：

Principal Component Analysis主成分分析：通過保留具備最大方差和互相不相關的特征之間的線性組合，可以生成數據集的低維表示。它還有助于理解無監督學習中的隱變量交互。

k-Means clusteringk 均值聚類：屬于硬聚類算法，根據數據到聚類中心的距離將其分成 k 個不同的簇。

Hierarchical clustering層次聚類：由于k-means算法始終有K值選擇和初始聚類中心點選擇的問題，而這些問題也會影響聚類的效果。為了避免這些問題，我們可以選擇另外一種比較實用的聚類算法，就是層次聚類算法。顧名思義，層次聚類就是一層一層的進行聚類，可以自頂向下把大的類別（cluster）分割，叫作分裂法；也可以自下而上對小的類別進行聚合，叫作凝聚法；但是一般用的比較多的是由下向上的凝聚方法。

以上就是一些幫助數據科學家理解數據基本的統計技術，了解這些基本分析技術將為為項目的開發和數據的理解帶來更多的益處，對數據的抽象和操作會變得更加容易。希望這篇文章能幫助小伙伴們在理解數據科學的路上帶來一些新的收獲。