牛頓環(huán)干涉簡介

干涉現(xiàn)象是光的波動說的有力證據(jù)之一。太陽光照射在肥皂泡或水面上的油膜時，呈現(xiàn)出的彩色條紋，就是光的干涉現(xiàn)象。要產(chǎn)生干涉，兩束光必須滿足相干條件：頻率相同、振動方向相同、相位差恒定。

實驗中獲得相干光的方法一般有兩種：分波陣面法和分振幅法。等厚干涉屬于分振幅法。

17世紀初，物理學家牛頓在制作天文望遠鏡時，偶然發(fā)現(xiàn)將一曲率半徑大的凸透鏡放在平面玻璃上時，其接觸點出現(xiàn)明暗相間圓環(huán)花樣，這是光的干涉現(xiàn)象，這種光學現(xiàn)象被稱為“牛頓環(huán)”。

由于牛頓是堅持光的微粒學說，未能對此做出解釋。牛頓環(huán)的干涉應用材料的球面度，平整度及光潔度的檢驗。

牛頓環(huán)干涉的基本原理

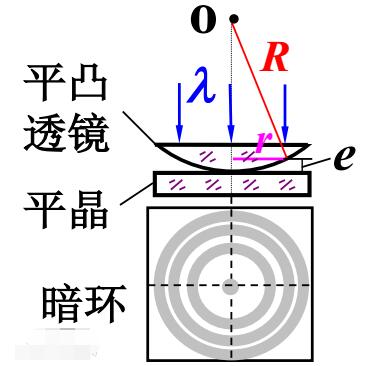
牛頓環(huán)裝置是由一塊曲率半徑較大的平凸面放在一塊光學玻璃平板（平鏡）上構(gòu)成的，如圖。平凸透鏡的凸面與玻璃平板之間的空氣層厚度從中心到邊緣逐漸增加，若以平行單光垂直照射到牛頓環(huán)上，則經(jīng)空氣層上、下表面反射的兩光束存在光程差，他們在平凸透鏡的凸面相遇后，將發(fā)生干涉。從透鏡上看到的干涉花樣是以玻璃接觸點為中心的一系列明暗相間的圓環(huán)，稱為牛頓環(huán)。同一干涉環(huán)上各處的空氣層厚度是相同的，因此他屬于等厚干涉。

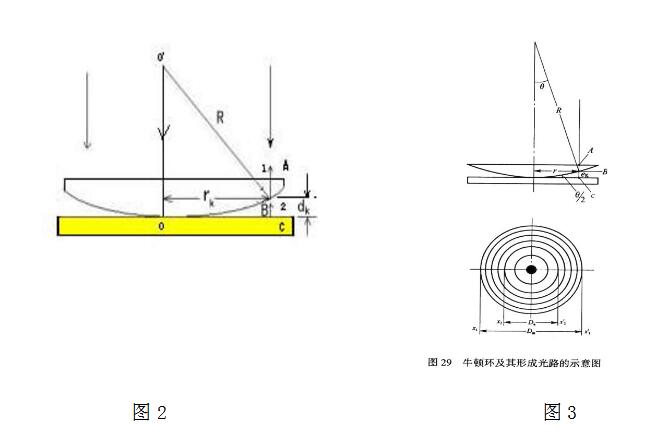
由圖2可見，若設透鏡的曲率半徑為R，與接觸點O相距為r處空氣層的厚度為d，其幾何關(guān)系式為

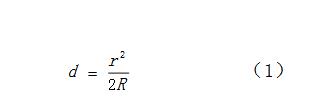
光線應是垂直入射的，計算光程差時還要考慮光波在平玻璃上反射會有半波損失，，從而帶來2?的附加程差，所以總光程差為

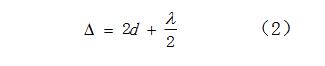
所以暗環(huán)的條件是

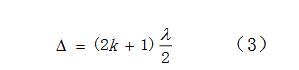
其中?3，2，1，0?k為干涉暗條紋的級數(shù)。綜合（1）（2）（3）式可得第可k級暗環(huán)的半徑為

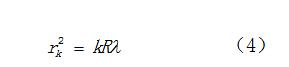
由式（4）可知，如果單色光源的波長λ已知，測出第m級的暗環(huán)半徑rm，，即可得出平圖透鏡的曲率半徑R；反之，如果R已知，測出rm后，就可計算出入射單色光波的波長λ。但是用此測量關(guān)系式往往誤差很大，原因在于凸面和平面不可能是理想的點接觸；接觸壓力會引起局部形變，使接觸處成為一個圓形平面，干涉環(huán)中心為一暗斑。或者空氣間隙層有了灰塵，附加了光程差，干涉環(huán)中心為一亮（或暗）斑，均無法確定環(huán)的幾何中心。實際測量時，我們可以通過測量距中心較遠的兩個暗環(huán)半徑rm和rn的平方差來計算曲率半徑R。因為

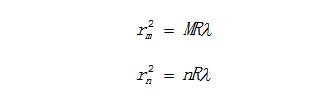
兩式相減可得

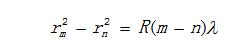
所以有

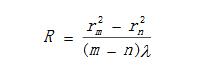
或

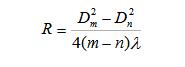
由上式可知，只要測出mD與nD（分別為第m與第n條暗紋的直徑）的值，就能算出R或λ。這樣就可避免實驗中條紋級數(shù)難以確定的困難，利用后以計算式還可克服確定條紋中心位置的困難。

牛頓環(huán)干涉的應用

判斷透鏡表面凸凹、精確檢驗光學元件表面質(zhì)量、測量透鏡表面曲率半徑和液體折射率。

在加工光學元件時，廣泛采用牛頓環(huán)的原理來檢查平面或曲面的面型準確度。

應用于光譜儀、把復合光分離成單色光的組成。