OpenAI 最近推出了其新的推理模型 o3，該模型在 ARC 數據集上大幅超越了之前的最佳性能（SOTA），并在具有挑戰性的 FrontierMath 數據集上取得了令人驚嘆的結果。很明顯，該模型在推理能力方面是一個重要的進步。

然而，最近關于人工智能進展停滯的報道中包含了一種對進展速度的悲觀情緒。許多人可能仍然在思考大型語言模型（LLM）擴展法則，這些法則預測計算、數據和模型大小的增加將導致更好的模型，是否已經“遇到了瓶頸”。我們是否達到了基于變換器的 LLMs 當前范式的可擴展性極限？

除了首次公開發布的推理模型（OpenAI 的 o1、Google 的 Gemini 2.0 Flash，以及即將在 2025 年發布的 o3）之外，大多數模型提供商似乎都在進行表面上看似漸進式的現有模型改進。從這個意義上說，2024 年基本上是一年的發展鞏固，許多模型在本質上已經趕上了年初的主流模型 GPT-4。

但這掩蓋了像 GPT-4o、Sonnet 3.5、Llama 3 等“主力”模型（即非推理模型）所取得的實際進展，這些模型在 AI 應用中最為頻繁。大型實驗室一直在推出這些模型的新版本，這些新版本在各個任務上都推動了 SOTA 性能，并且在編程和解決數學問題等任務上帶來了巨大的改進。

不可忽視的是，2024 年模型性能的改進主要是由訓練后和測試時計算的擴展所驅動的。在預訓練方面，新聞并不多。這導致了一些猜測，即（預訓練）擴展法則正在崩潰，我們已經達到了當前模型、數據和計算所能達到的極限。

在這篇文章中，將回顧 LLM 擴展法則的歷史，并分享對未來方向的看法。從外部預測大型 AI 實驗室的進展是困難的。對 2025 年 LLM 擴展可能如何繼續的總結：

預訓練：有限 - 計算擴展正在進行中，但我們可能受限于足夠規模的新高質量數據；

訓練后：更有可能 - 合成數據的使用已被證明非常有效，這可能會繼續下去；

推理時：也很有可能 - OpenAI 和 Google/Deepmind 在今年開始了這一趨勢，其他參與者將跟進；同時，注意開源復制；在應用層面，我們將看到越來越多的代理產品。

什么是 LLM 擴展法則？

在深入探討之前，什么是 LLM 擴展法則？簡而言之：它們是關于規模（以計算、模型大小和數據集大小衡量）與模型性能之間相關性的經驗觀察。

有了這個背景，讓我們看看我們目前的位置以及我們是如何走到這一步的。

計算最優的預訓練 - Kaplan 和 Chinchilla

最初的擴展法則指的是 LLMs 的預訓練階段。Kaplan 擴展法則（OpenAI，2020）建議，隨著、預訓練計算預算增加，應該更多地擴展模型大小而不是數據。這意味著：給定 10 倍的訓練預算增加，應該將模型大小擴展 5.5 倍，數據擴展 1.8 倍。

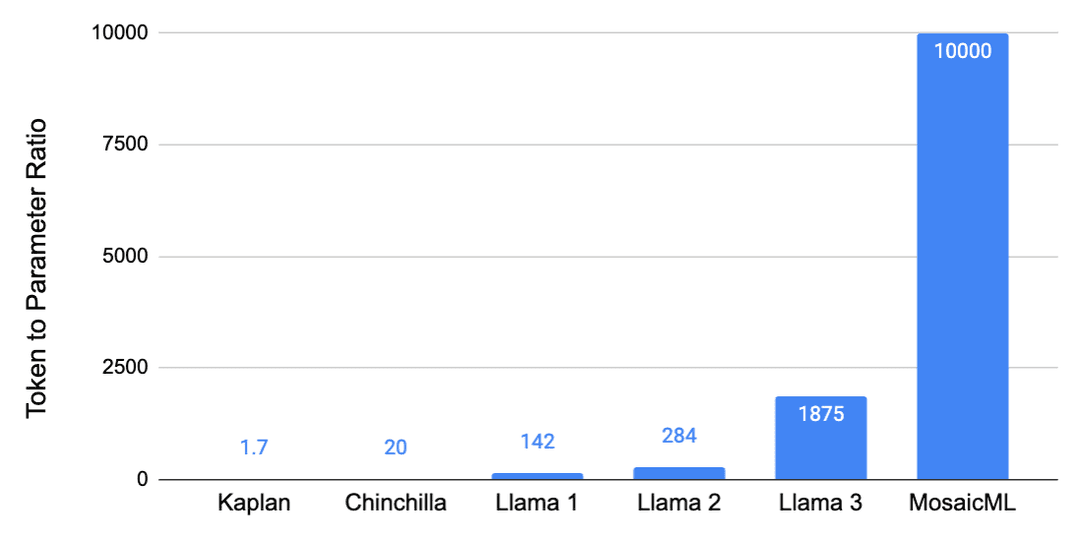
2020 年由 OpenAI 發布的 GPT-3，很可能遵循了這些擴展法則，并且在給定其大小的情況下，訓練數據量異常少。也就是說，它有 1750 億參數，但僅在 3000 億token上進行了訓練，這相當于大約 1.7 個token/參數。

這些原始擴展法則存在一些缺陷，例如沒有考慮嵌入參數，并且通常使用相對較小的模型來估計擴展法則，這并不一定適用于大型模型。Chinchilla 擴展法則（Deepmind，2022）糾正了一些這些缺陷，并得出了非常不同的結論。

特別是，數據的重要性比以前認為的要大得多，因此模型大小和數據應該與計算同等比例地擴展。這些新發現表明，像 GPT-3 和當時發布的其他模型實際上是嚴重欠擬合的。一個像 GPT-3 這樣的 1750 億參數的模型應該在大約 3.5T token上進行訓練才能達到計算最優，這大約是 20 個token/參數。或者，通過反向論證，像 GPT-3 這樣的模型應該小 20 倍，即只有 150 億參數。

Chinchilla 陷阱：優化推理

僅僅遵循 Chinchilla 擴展法則會導致“Chinchilla 陷阱”，即你最終會得到一個太大、因此在大規模推理時運行成本過高的模型。例如，在 Touvron 等人（Meta，2023）的 Llama 1 論文中，指出損失在 Chinchilla 最優之后繼續下降。Llama 1 模型以高達 142 個token/參數的比例進行訓練，這是最小的（70 億）模型，訓練在 1T 標記上。這一趨勢繼續出現在 Llama 2（Meta，2023）中，token翻倍至 2T，導致高達 284 個token/參數的比例。最后，也在 Llama 3（Meta，2024）中出現，比例高達 1,875 個token/參數（80 億模型在 15T tokne上訓練）。訓練這些小型模型更長時間使它們達到出人意料地高性能，且在推理時運行成本較低。

這種證據不僅來自 Llama 3 模型訓練在極高的token參數比例上，而且來自文獻。例如，Sardana 等人（MosaicML，2023）估計了考慮推理時計算的擴展法則。在他們的實驗中，他們訓練了高達 10,000 個token/參數 的模型比例，并發現損失在 Chinchilla 最優之后繼續下降。這些圖表很好地說明了訓練小型模型更長時間的點，以及如何導致如果預期有足夠高的推理需求，總成本更低。

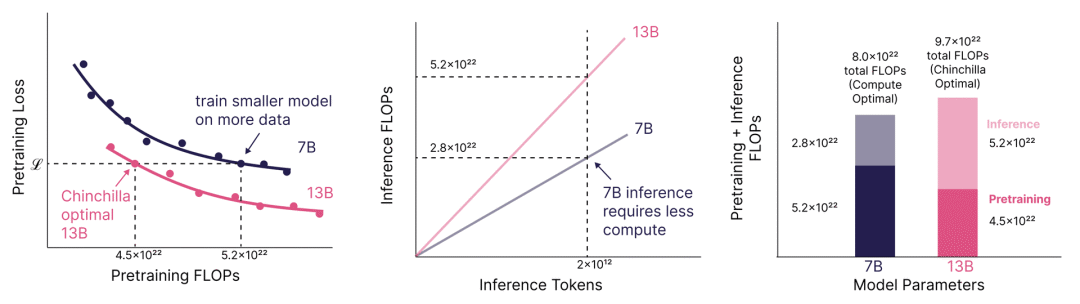
Sardana et al. (2023)

測試時間計算擴展

不用說，隨著數據和參數越來越多地訓練模型，計算成本越來越高。在 Llama 3 論文中，旗艦模型的訓練使用了 3.8×10^25 FLOPs，這是 Llama 2 的 50 倍。根據 EpochAI，截至 2024 年 12 月，已知的最大訓練預算是在 Gemini Ultra 的情況下，為 5×10^25 FLOPs。計算量非常大，尤其是如果考慮將其擴大幾個數量級的話。

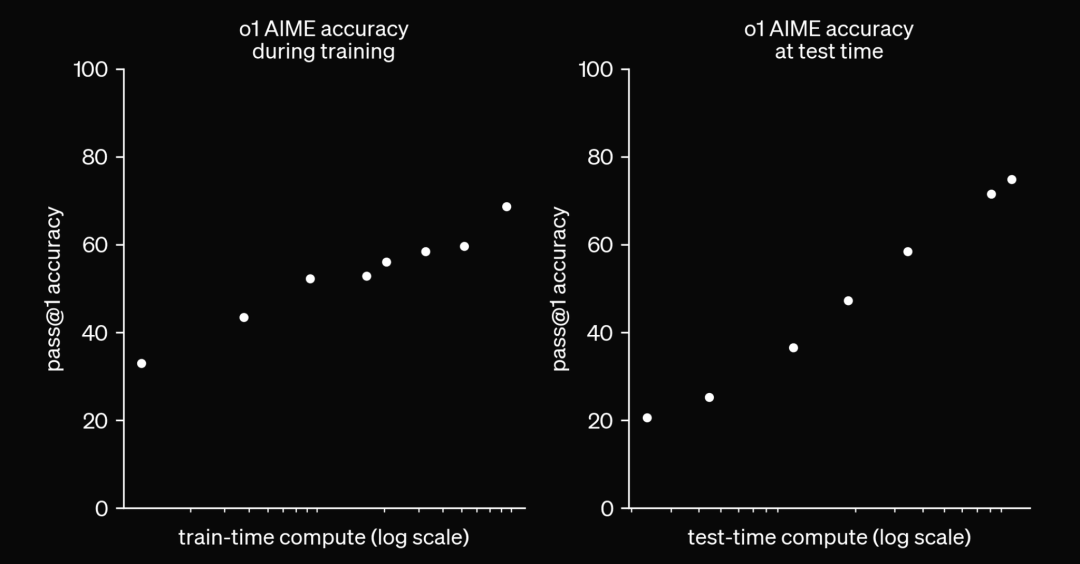
OpenAI 2024

作為回應，2024 年發布了像 OpenAI 的 o1 和最近的 o3 這樣的模型，這些模型利用測試時計算來生成預測。所以，這些模型不是立即生成答案，而是在測試時生成思維鏈，或使用 RL 技術來生成更好的答案。通俗地說，可以說我們給了模型更多時間來“思考”再給出答案。這催生了一種完全不同的 LLM 擴展法則，即測試時計算。

推薦聽聽 OpenAI 的 Noam Brown 的有趣演講，他談到了他在訓練用于玩撲克、國際象棋、Hex 等游戲的模型時學到的經驗，以及測試時計算如何使 SOTA 性能成為可能，這些性能僅通過擴展訓練計算是無法實現的。

例如，如果存在訓練和推理時間計算之間的權衡，即可以用 10 倍的訓練預算換取 15 倍的推理時間計算增加，那么在訓練計算已經非常昂貴而推理計算非常便宜的情況下，這樣做是有意義的。

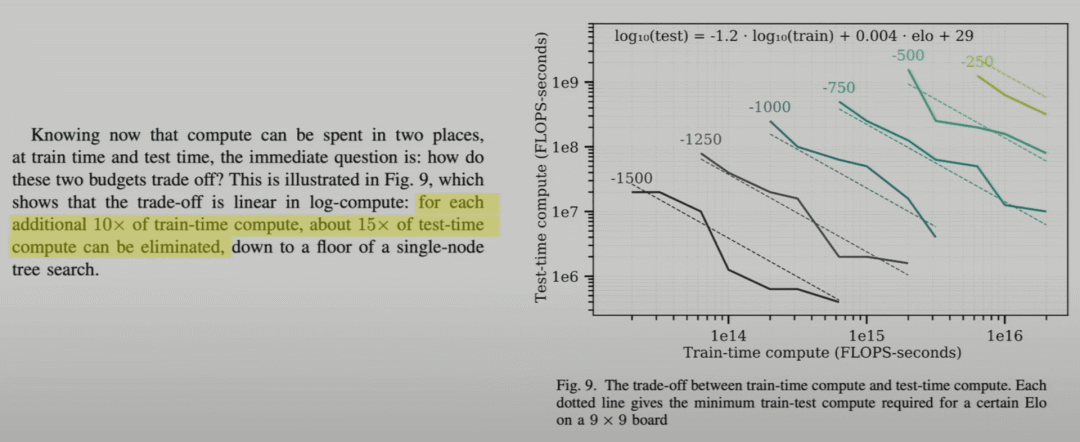
Jones (2021)

擴展法則是否仍然有效，還是我們已經遇到了瓶頸？

這是個大問題，從大型實驗室外部很難回答。讓我們回顧一下他們內部的說法，同時要意識到他們的陳述可能存在一些偏見。

Anthropic 的 Dario Amodei 表示：“我見過這種情況發生很多次，真的相信擴展可能會繼續，而且其中有一些我們還沒有在理論上解釋清楚的魔力。”

OpenAI 的 Sam Altman 則表示：“沒有遇到瓶頸。”

此外，公司仍在擴大他們的數據中心，xAI 的 Colossus 集群托管了 10 萬個 H100 節點，并計劃將其擴展到至少 100 萬個。

盡管在擴展計算能力時存在工程挑戰和能源瓶頸，但這一過程正在進行中。然而，計算能力只是 LLM 擴展法則中的一個因素，另外兩個因素是模型大小和數據。有了更大的集群，也可以在給定時間內訓練更大的模型。不過，數據的擴展則是另一回事。

EpochAI 估計，在索引的網絡中有 510T 個token的數據可用，而已知的最大數據集是大約 18T 個token（Qwen2.5）。看起來似乎還有很大的空間可以擴展數據，但其中大部分數據質量較低或重復。再加上從 1-2 年前開始，互聯網上新增的大量文本是由 LLM 生成的。盡管還有可能的新數據源可用，例如轉錄互聯網上的所有視頻，或者使用不在開放互聯網上的文本（例如專有數據），但低垂的果實已經被采摘了。

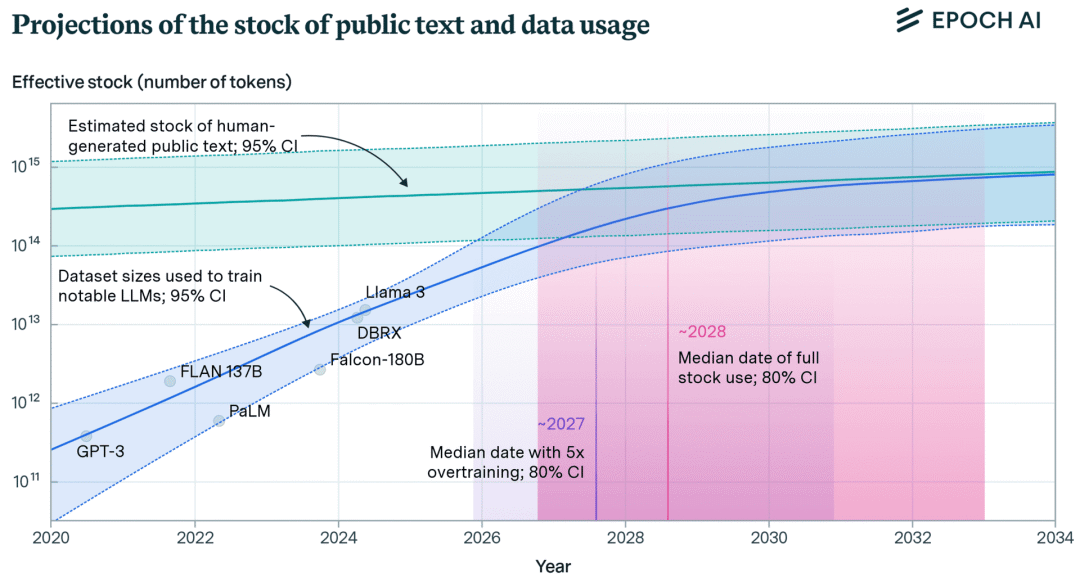
EpochAI

擴展的邊際效益遞減實際上正是冪律關系所預期的。也就是說，為了獲得第一單位的改進，需要 1 單位的數據，然后是 10 單位用于下一個改進，接著是 100 單位，以此類推。正如 Yann LeCun 所說，這適用于所有“長尾”領域，即隨著數據集大小的增加，輸入的多樣性不斷增長的領域，如對話和問答。

從擴展法則的方程式和圖表來看，應該清楚地認識到這些關系是有極限的，這一點也得到了 Kaplan 原始論文[3]的認可。原因在于自然語言中固有的熵，以及損失無法降低到零。因此，雖然目前看來性能似乎只是隨著計算、數據、模型大小的對數線性增長，但最終它必須趨于平穩。問題不在于是否會趨于平穩，而在于何時會發生。

我們現在已經達到了這個點了嗎？很難回答，因為這不僅僅是簡單地將計算或數據再擴展一個數量級并看看會發生什么。AI 實驗室正在構建大型的新集群，這將使他們能夠更長時間地訓練模型，并觀察損失是否繼續以相同的速度減少。據我們所知，我們還沒有在 10 萬個 H100 節點上訓練這些模型，更不用說 100 萬個了，所以很難判斷我們還能將訓練損失降低多少。更重要的是，我們只有一個互聯網，所以擴展數據是一個更困難的問題。正如我們從 Kaplan 擴展法則中知道的，只有當模型不受這些因素之一的限制時，這些法則才成立。

Ilya Sutskever在NeurIPS 2024

然而，鑒于那些利用測試時計算的模型所表現出的令人印象深刻的表現，以及OpenAI 的 o3 的發布，很明顯，擴展測試時計算是未來的發展趨勢。

如下面的圖表所示，當擴展測試時計算時，在具有挑戰性的 Arc 數據集上的性能提升是相當顯著的。從 o3 low到 o3 high，模型被賦予了 172 倍更多的計算資源來生成答案。它平均每道題使用 5700 萬個token，相當于 13.8 分鐘的運行時間，而在低計算設置中，它每道題僅使用 33 萬個token，即每道題 1.3 分鐘。

根據 Noam Brown 的說法，這只是開始。明年，我們可能會讓模型運行數小時、數天甚至數周來回答真正具有挑戰性的問題。

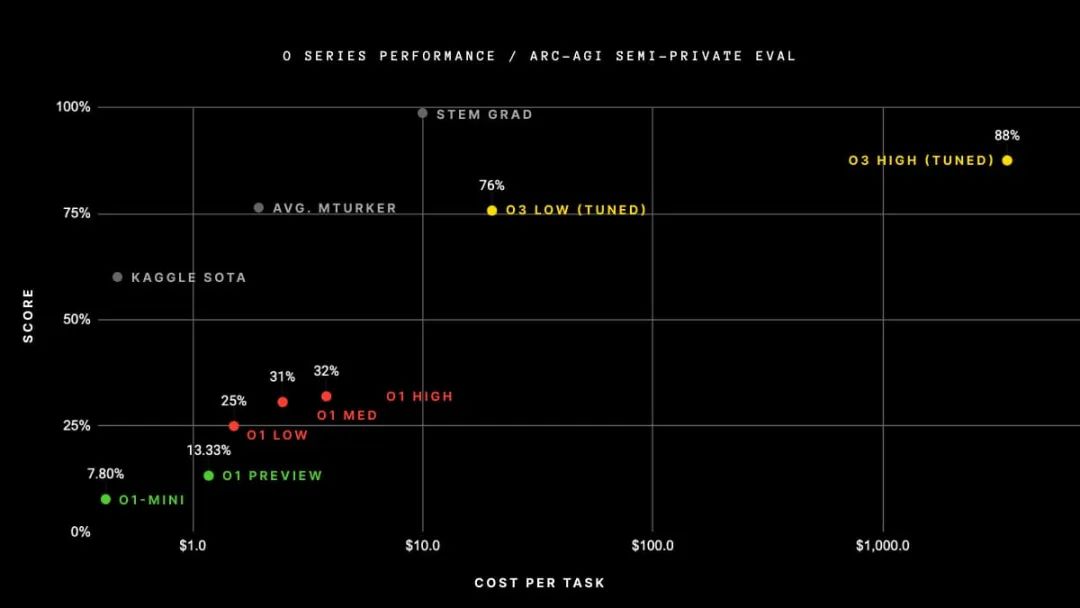
Arc Prize網站

結論

鑒于目前的發展勢頭和硬件部署情況，人們將會嘗試通過投入更多的計算資源來進一步推動擴展法則。這可能是在訓練方面，通過延長預訓練時間或在訓練后投入更多資源，但尤其在推理方面，通過讓模型“思考”更長時間后再給出答案。

公眾可能并不總是能夠接觸到最大的模型，這些模型可能性能最佳，但運行成本過高。像 GPT4o 或 Sonnet 3.5 這樣的模型，可能更適合用于推理的小型模型。而擁有 4050 億參數的 Llama 3 模型，雖然相當龐大，但可以作為小型模型的優秀教師模型，或者用于生成合成數據。

今年的趨勢，肯定會延續到 2025 年（在一年的這個時間點上，這是一個容易做出的預測）：

代理（Agents）

測試時計算（Test-time compute）

合成數據（Synthetic data）

代理實際上也是測試時計算的一種方式，但這種方式比大型實驗室更易于公眾和應用開發者接觸。盡管如此，大型實驗室也在大力投資代理技術。

測試時計算是關鍵。正如我們在 o1 Gemini 2.0 Flash 和 o3 中所看到的，這些將是解決需要更復雜推理的用例，或者在需要權衡一些訓練計算以換取更多推理計算的情況下的解決方案。

至于合成數據，它主要用于訓練后，但也可以將清理互聯網視為一種合成數據生成的方式。從今年的 LLM 論文中可以看出，合成數據對于 SFT 在數學和編程等任務上的性能提升非常重要。在某些領域，合成數據比其他領域更有用，所以不確定它是否真的能夠填補人類撰寫數據缺失的空白。

因此，本文的結論是，我們可能已經達到了一個點，即預訓練擴展法則并沒有完全崩潰，但可能正在放緩，這并不令人驚訝。這主要是因為我們已經耗盡了大量高質量文本的來源。

然而，這并不意味著該領域不會再有任何進展，因為預訓練只是拼圖的一部分。正如我們所見，擴展測試時計算和使用合成數據，很可能是未來進展的主要驅動力。至少到目前為止，我們可能只是處于測試時擴展法則的早期階段，所以還有很大的改進空間。

總之，這是我們看到的 2025 年 LLM 擴展最具潛力的方向：

預訓練：有限 - 計算擴展正在進行中，但我們可能受限于足夠規模的新高質量數據；

訓練后：更有可能 - 合成數據的使用已被證明非常有效，這可能會繼續下去；

推理時：也很有可能 - OpenAI 和 Google/Deepmind 在今年開始了這一趨勢，其他參與者將跟進；同時，注意開源復制；在應用層面，我們將看到越來越多的代理產品。

參考文獻：

[1] T. Brown et al. Language Models are Few-Shot Learners, 2020.[paper]

[2] J. Hoffmann et al. Training Compute-Optimal Large Language Models, 2022.[paper]

[3] J. Kaplan et al. Scaling Laws for Neural Language Models, 2020.[paper]

[4] H. Touvron et al. LLaMA: Open and Efficient Foundation Language Models, 2023.[paper]

[5] H. Touvron et al. Llama 2: Open Foundation and Fine-Tuned Chat Models, 2023.[paper]

[6] Llama Team, AI @ Meta. The Llama 3 Herd of Models, 2024.[paper]

[7] N. Sardana et al. Beyond Chinchilla-Optimal: Accounting for Inference in Language Model Scaling Laws, 2024.

原文鏈接：https://www.jonvet.com/blog/llm-scaling-in-2025