漢明碼原理介紹:
在計算機運行過程中,由于種種原因導致數據在存儲過程中可能出現差錯,為了能夠及時發現錯誤并且將錯誤糾正,通常可以將原數據配成漢明編碼。
漢明碼具有一位糾錯能力。
奇偶校驗是一種添加一個奇偶位用來指示之前的數據中包含有奇數還是偶數個1的檢驗方式。如果在傳輸的過程中,有奇數個位發生了改變,那么這個錯誤將被檢測出來(注意奇偶位本身也可能改變)。一般來說,如果數據中包含有奇數個1的話,則將奇偶位設定為1;反之,如果數據中有偶數個1的話,則將奇偶位設定為0。換句話說,原始數據和奇偶位組成的新數據中,將總共包含偶數個1.
奇偶校驗并不總是有效,如果數據中有偶數個位發生變化,則奇偶位仍將是正確的,因此不能檢測出錯誤。而且,即使奇偶校驗檢測出了錯誤,它也不能指出哪一位出現了錯誤,從而難以進行更正。數據必須整體丟棄并且重新傳輸。在一個噪音較大的媒介中,成功傳輸數據可能需要很長時間甚至不可能完成。雖然奇偶校驗的效果不佳,但是由于他只需要一位額外的空間開銷,因此這是開銷最小的檢測方式。并且,如果知道了發生錯誤的位,奇偶校驗還可以恢復數據。
如果一條信息中包含更多用于糾錯的位,且通過妥善安排這些糾錯位使得不同的出錯位產生不同的錯誤結果,那么我們就可以找出出錯位了。在一個7位的信息中,單個數據位出錯有7種可能,因此3個錯誤控制位就足以確定是否出錯及哪一位出錯了。
漢明編碼方案通用算法
下列通用算法可以為任意位數字產生一個可以糾錯一位的漢明碼。
一、1開始給數字的數據位(從左向右)標上序號, 1,2,3,4,5.。。
二、將這些數據位的位置序號轉換為二進制,1, 10, 11, 100, 101,等。
三、數據位的位置序號中所有為二的冪次方的位(編號1,2,4,8,等,即數據位位置序號的二進制表示中只有一個1)是校驗位
四、有其它位置的數據位(數據位位置序號的二進制表示中至少2個是1)是數據位
五、每一位的數據包含在特定的兩個或兩個以上的校驗位中,這些校驗位取決于這些數據位的位置數值的二進制表示
1.校驗位1覆蓋了所有數據位位置序號的二進制表示倒數第一位是1的數據:1(校驗位自身,這里都是二進制,下同),11,101,111,1001,等
2.校驗位2覆蓋了所有數據位位置序號的二進制表示倒數第二位是1的數據:10(校驗位自身),11,110,111,1010,1011,等
3.校驗位4覆蓋了所有數據位位置序號的二進制表示倒數第三位是1的數據:100(校驗位自身),101,110,111,1100,1101,1110,1111,等
4.校驗位8覆蓋了所有數據位位置序號的二進制表示倒數第四位是1的數據:1000(校驗位自身),1001,1010,1011,1100,1101,1110,1111,等
5.簡而言之,所有校驗位覆蓋了數據位置和該校驗位位置的二進制與的值不為0的數。 采用奇校驗還是偶校驗都是可行的。偶校驗從數學的角度看更簡單一些,但在實踐中并沒有區別。
從編碼形式上,我們可以發現漢明碼是一個校驗很嚴謹的編碼方式。在這個例子中,通過對4個數據位的3個位的3次組合檢測來達到具體碼位的校驗與修正目的(不過只允許一個位出錯,兩個出錯就無法檢查出來了,這從下面的糾錯例子中就能體現出來)。在校驗時則把每個漢明碼與各自對應的數據位值相加,如果結果為偶數(糾錯代碼為0)就是正確,如果為奇數(糾錯代碼為1)則說明當前漢明碼所對應的三個數據位中有錯誤,此時再通過其他兩個漢明碼各自的運算來確定具體是哪個位出了問題。
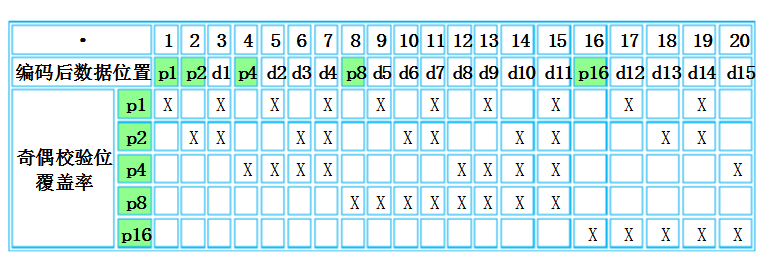
觀察上表可發現一個比較直觀的規律:第i個檢驗位是第2i-1位,從該位開始,檢驗2i-1位,跳過2i-1位……依次類推。例如上表中第3個檢驗位p4從第23-1=4位開始,檢驗4、5、6、7共4位,然后跳過8、9、10、11共4位,再檢驗12、13、14、15共4位……
漢明碼的編碼規則如下:
在新的編碼的2^(k - 1)( k 》= 0)位上填入0(即校驗位)
把新的編碼的其余位把源碼按原順序填入
校驗位的編碼方式為:第k位校驗碼從則從新的編碼的第2^(k - 1)位開始,每計算2^(k - 1)位的異或,跳2^(k - 1)位,再計算下一組2^(k - 1)位的異或,填入2^(k - 1)位,比如:
第1位校驗碼位于新的編碼的第1位(2 ^(1-1) == 1)(漢明碼從1位開始),計算1,3,5,7,9,11,13,15,。。。位的異或,填入新的編碼的第1位。
第2位校驗碼位于新的編碼的第2位(2 ^(2-1) == 2),計算2,3,6,7,10,11,14,15,。。。位的異或,填入新的編碼的第2位。
第3位校驗碼位于新的編碼的第4位(2 ^(3-1) == 4),計算4,5,6,7,12,13,14,15,20,21,22,23,。。。位的異或,填入新的編碼的第4位。
第4位校驗碼位于新的編碼的第8位(2 ^(4-1) == 8),計算8-15,24-31,40-47,。。。位的異或,填入新的編碼的第8位。
第5位校驗碼位于新的編碼的第16位(2 ^(5-1) == 16),計算16-31,48-63,80-95,。。。位的異或,填入新的編碼的第16位。
在數學方面,漢明碼是一種二元線性碼。對于每一個整數m》2,存在一個編碼,帶有m個奇偶校驗位2m- m-1個數據位。
漢明碼的生成和檢驗
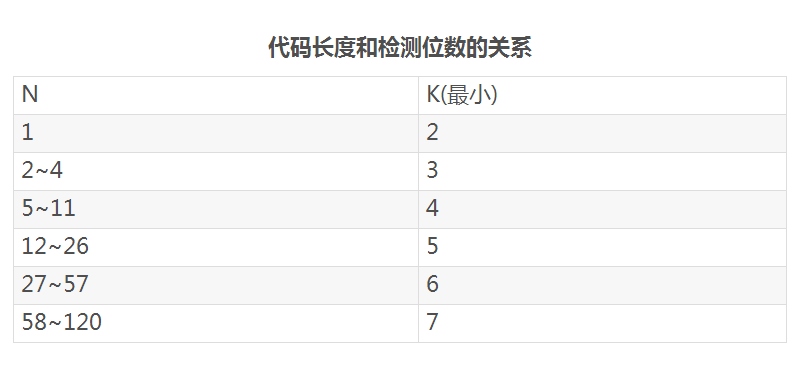
設將要進行檢測的二進制代碼為n位,為使其具有糾錯能力,需要再加上k位的檢測位,組成n+k位的代碼。那么,新增加的檢測位數k應滿足:
2k≥n+k+1或2k-1≥n+k
當k的位數確定后,便可根據承擔的檢測任務設定他們在傳送代碼中的位置和他們的取值。首先,將所要檢測的代碼分為Pn組,分多少個組,我們通過k的值來確定。下面我用一個例子來說明。
假設將要進行檢測的二進制代碼為0101,位數n=4,根據公式2k≥n+k+1可以得出k的值是3,所以最終形成的漢明碼應為n+k=7位。
所以分組分為P1、P2、P4。原因則是第一組是20、第二組則是21 、同理第三組則是22 、依次列推分組應按照2k-1。同時以后根據分組產生的數插入的位置也是按照此規律插入,比如第一組插入20、即第1位,第二組插入21 、即第2位,以此類推。那么組分好了,他們每一組中包含的位則是:
p1包含(1,3,5,7,9,11,。。。位)
p2包含(2,3,6,7,10,11,14,15,。。。位)
p3包含(4,5,6,7,12,13,14,15,。。。位)
每一組中包含的數又是如何確定的呢?我們來看下面這個表格

將編號轉成二進制從右向左,如果第一位是1,例如編號是1,3,5,7.。。。的就分入第一組,如果第二位是1的,例如編號2,3,6,7,10.。。的就分入第二組,以此類推將所有的編號分入相應的組中。下面我么來看例子0101是如何產生漢明碼的(采用配偶原則),
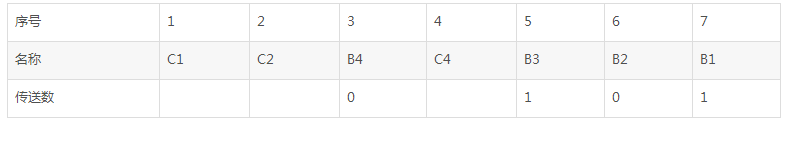
其中C1、C2、C4是我們插入的檢測位
如果按照配偶原則來配置漢明碼,則C1應使1 3 5 7位中“1”的個數為偶數;C2應使2 3 6 7位中“1”的個數為偶數;C4應使4 5 6 7位中“1”的個數為偶數。
按照上面我所說的則:
C1=③位+⑤位+⑦位,即C1=B4+B3+B1=0+1+1=0
C2=③位+⑥位+⑦位,即C2=B4+B2+B1=0+0+1=1
C4=⑤位+⑥位+⑦位,即C4=B3+B2+B1=1+0+1=0
所以0101的漢明碼應為C1C2B4C4B3B2B1,即0100101
漢明碼還存在配奇原則,下面來講一講配奇原則。按照配奇原則配置1100101的漢明碼。
根據1100101可知n=7。根據公式我們可以求出需要添加k=4位檢測位,詳細情況如下表。

按配奇原則配置,則
C1=③位+⑤位+⑦位+⑨位+11位+1=1+1+0+1+1+1=1
C2=③位+⑥位+⑦位+10位+11位+1=1
C4=⑤位+⑥位+⑦位+1=0
C8=⑨位+10位+11位+1=1
所以按配奇原則新配置的漢明碼為11101001101
漢明碼校驗錯誤實例
我們以上面的編碼為例,假設我們現在收到的編碼為001101001,我們可以發現漢明碼的第8位與原來的漢明碼001101011不同,那我們怎么找出這個第8位的錯誤編碼呢?
算法很簡單,我們只要在算漢明碼校驗位的算法的上再算一遍,就得到了漢明碼的校驗方法,比如計算001101001對應的2^k位。
1,3,5,7,9進行異或,得到0
2,3,6,7進行異或,得到0
4,5,6,7進行異或,得到0
8,9進行異或,得到1
我們把上述結果反著排列,得到1000,即十進制的8,根據漢明碼的校驗規則,編碼出錯的地方即在第8位,我們把第8位的0換成1,即可得原來的編碼001101011。
上述的例子是出現在2^k的校驗位上的,如果出現在非2^k位上,得到的結果也是一樣的,比如:
假設收到的編碼為001100011,即第6位出了錯誤,我們根據規則
1,3,5,7,9進行異或,得到0
2,3,6,7進行異或,得到1
4,5,6,7進行異或,得到1
8,9進行異或,得到0
我們把上述結果反著排列,得到0110,即十進制的6,根據漢明碼的校驗規則,編碼出錯的地方即在第6位,我們把第6位的0換成1,即可得原來的編碼001101011。
漢明碼的編碼和校驗的C++實現
通過原理,我們可以很簡單地實現漢明碼的編碼和校驗代碼
auto cal(size_t sz)-》decltype(auto)
{
decltype(sz) k = 0;
decltype(sz) cur = 1;
while (cur - 1 《 sz + k )
{
cur 《《= 1;
k++;
}
return k;
}
bool encode(const string &s, string &d)
{
d.clear();
auto k = cal(s.size());
d.resize(s.size() + k);
for (decltype(d.size()) i = 0, j = 0, p = 0; i!= d.size();i++)
解碼與校驗:
auto antiCal(size_t sz)-》decltype(auto)
{
decltype(sz) k = 0;
decltype(sz) cur = 1;
while (cur 《 sz)
{
cur 《《= 1;
k++;
}
return k;
}
auto decode(string &s, string &d)-》decltype(auto)
{
s.clear();
auto k = antiCal(d.size());
s.resize(d.size() - k);
decltype(d.size()) sum = 0;
for (decltype(k) p = 0;p != k;p++)
{
int pAnti = 0;
decltype(k) index = 1 《《 p;
for (decltype(d.size()) i = index - 1;i 《 d.size(); i+=index)
{
for (auto j = 0; j 《 index && i 《 d.size(); i++, j++)
pAnti ^= d[i] - ‘0’;
}
sum += pAnti 《《 p;
}
if (sum != 0)
d[sum - 1] = (1- (int)(d[sum - 1] - ‘0’)) + ‘0’;
for (decltype(d.size()) i = 0, p = 0,j = 0; i != d.size(); i++)
{
if ((i + 1) == (1 《《 p) && p 《 k)
p++;
else
s[j++] = d[i];
}
return sum;
}
{
if ((i + 1) == pow(2,p) && p 《 k)
{
d[i] = ‘0’;
p++;
}
else if (s[j] == ‘0’ || s[j] == ‘1’)
d[i] = s[j++];
else
return false;
}
for (auto i = 0; i != k;i++)
{
int count = 0 ,index = 1 《《 i;
for (auto j = index - 1; j 《 d.size() ;j += index)
for (auto k = 0; k!= index && j 《 d.size(); k++, j++)
count ^= d[j] - ‘0’;
d[index - 1] = ‘0’ + count;
}
return true;
}
測試樣例:
int main()
{
string source, dest;
while (cin 》》 source)
{
if (encode(source,dest))
{
cout 《《 “Source: ” 《《source 《《 endl;
cout 《《 “Dest: ” 《《 dest 《《 endl;
}
size_t index;
cout 《《 “----input error index : ”;
cin 》》 index;
auto k = dest.size();
if (index != 0 && index 《= dest.size())
dest[index - 1] = (1 - (int)(dest[index - 1] - ‘0’)) + ‘0’;
cout 《《 “Code ” 《《 dest 《《endl;
auto ret = decode(source,dest);
if (ret == 0)
{
cout 《《 “Source: ” 《《source 《《 endl;
cout 《《 “Dest: ” 《《dest 《《 endl;
}
else
{
cout 《《 “Error index ”《《 ret 《《 endl;
cout 《《 “Corret source: ” 《《source 《《 endl;
cout 《《 “Corret dest: ” 《《dest 《《 endl;
}
cout 《《 endl;
}
return 0;
}
Source: 10101
Dest: 001101011
----input error index : 8
Code 001101001
Error index 8
Corret source: 10101
Corret dest: 001101011
Source: 1001010101010101010111111001101
Dest: 1111001101010100101010101111110101101
----input error index : 20
Code 1111001101010100101110101111110101101
Error index 20
Corret source: 1001010101010101010111111001101
Corret dest: 1111001101010100101010101111110101101
Source: 1
Dest: 111
----input error index : 0
Code 111
Source: 1
Dest: 111
-
漢明碼
+關注
關注
0文章
8瀏覽量
8096
發布評論請先 登錄
相關推薦
基于FPGA的漢明碼譯碼器如何對碼元數據添加噪聲干擾?
【原創】基于FPGA的漢明碼編碼解碼設計
提高漢明碼對突發干擾的糾錯能力
一種基于漢明碼和濕紙碼的隱寫算法
基于FPGA的檢糾錯邏輯算法的實現

漢明碼計算及其糾錯原理詳解
漢明碼糾錯的基本原理及優化解決方案





 漢明碼原理和校驗及實現
漢明碼原理和校驗及實現











評論