一般來說,我們會從時域和頻域兩個角度,分別對信號進行分析。
時域
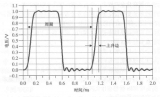
時域是真實世界存在的域,按時間順序呈現。例如,在某個時鐘信號的時域圖中,可以觀察到兩個重要的參數,波形的周期和上升沿:
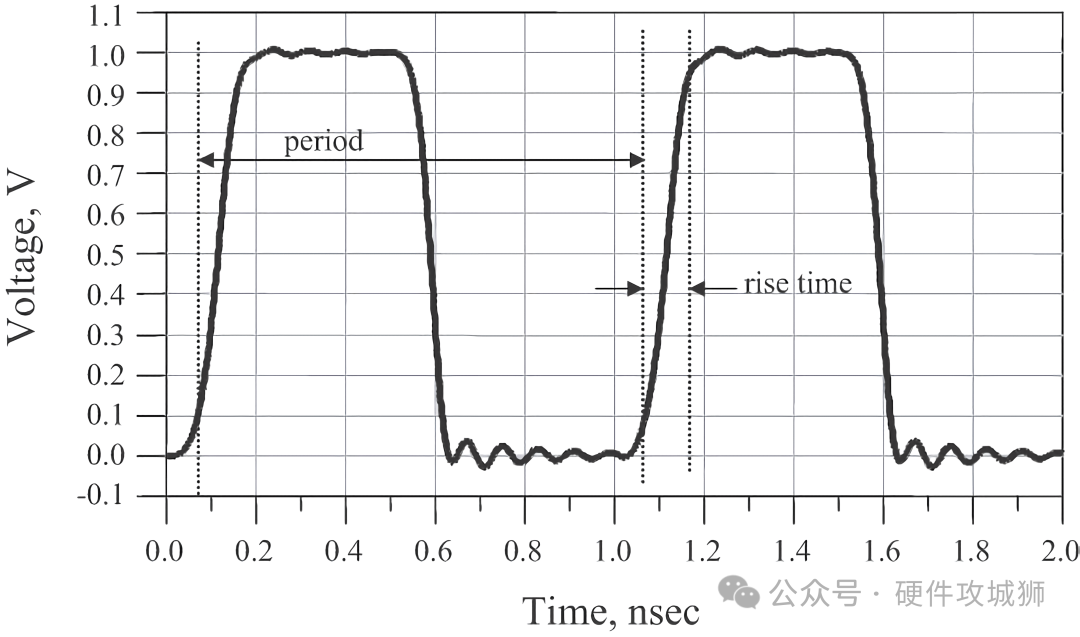
時鐘周期即信號循環重復一次所花的時間,通常它的單位是納秒級,時鐘頻率就是 1s 內循環的次數,即周期的倒數。例如,周期為 1ns 的時鐘信號,頻率就是 1/10ns=0.1GHz。
上升沿,通常定義為信號以最高點為標準的 20% 跳變到 80% 所花的時間(有時也會定義為 10% 到 90%)。下降沿通常比上升沿要短,這是因為典型 CMOS 結構中,N-MOS 比 P-MOS 導通速度要快,所以下降沿通常比上升沿短,也更容易產生信號完整性問題。
頻域
頻域是一個存在于數學定義中的域。通常在頻域中使用正弦波,因為時域中的任何波形,都能用正弦波合成出來。
頻域可以用更簡潔的語言描述相同的信息。如下圖可見,左邊是時域中對正弦波的描述,正弦波可以用頻率、幅度、相位這 3 個參數完全表示出來;而右邊是頻域中的描述,頻率和幅度可以僅用一個點表示出來(在大多數場合會忽略相位的使用):
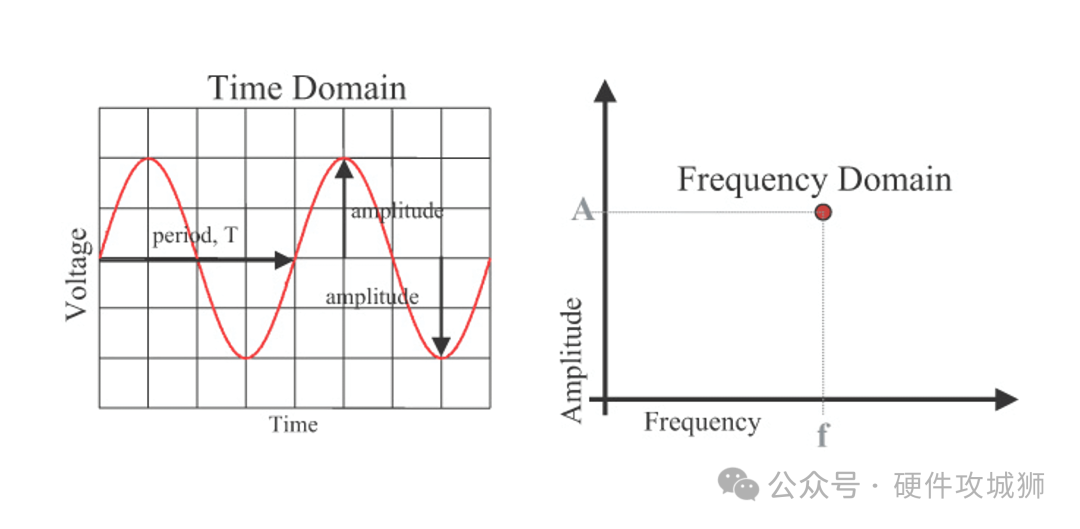
這樣,在頻域中表示一個正弦波就只需要一個點。如果有若干個頻率點,那么這個集合就稱為頻譜。
將一般互連的電氣問題放在頻域中,并使用正弦波描述,會變得更容易理解并解決。
時域到頻域的變換
從時域到頻域,轉換方法就是傅里葉變換。傅變有三種類型:傅里葉積分(FI)、離散傅里葉變換(DFT)、快速傅里葉變換(FFT)。
傅里葉積分用于將時域內的理想數學表達式變換為頻域表示,是將時域時間軸從負無窮到正無窮積分,得出從零到正無窮上連續的頻域函數。
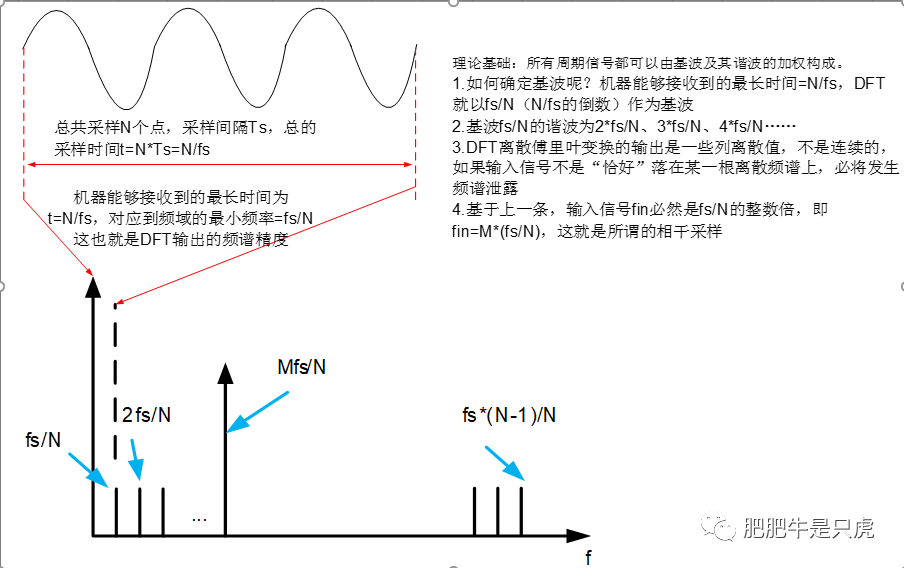
但實際上時域的波形是由一系列離散點組合而成的。這時候使用離散傅里葉變換,可以把波形轉換到頻域中(前提是時域為周期性的)。不比傅里葉積分,傅里葉變換只需要通過求和就可以實現轉換。
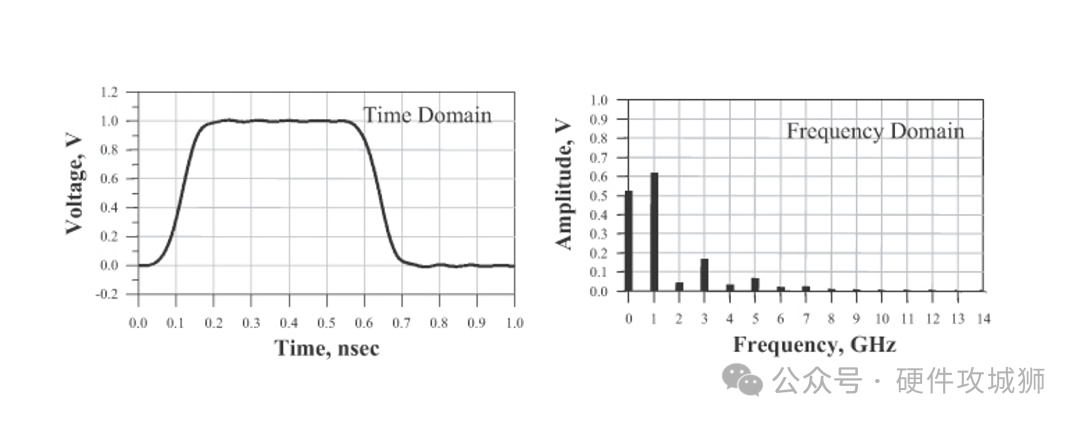
快速傅里葉變換使用了快速矩陣代數學的方法,只應用于時域中數據點個數是 2 的整數次冪的情況(如 256、512、1024 點)。根據計算點個數的數量,計算速度可以比普通離散傅里葉變換快很多。
需要注意的是,快速傅里葉變換要求信號是周期重復的,所以需要對原始信號進行相干采樣,或在采樣后加窗處理。
頻域到時域的逆變換
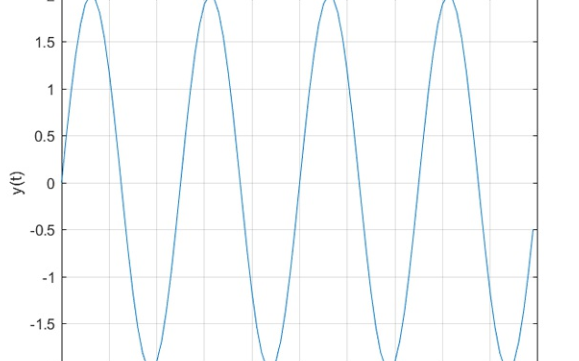
頻域包含波形中所有正弦波的頻率和幅度,如果要獲取它的時域波形,那么只需要將每個頻率分量逆變換乘它的時域正弦波,再疊加起來即可,這個過程稱為傅里葉逆變換。
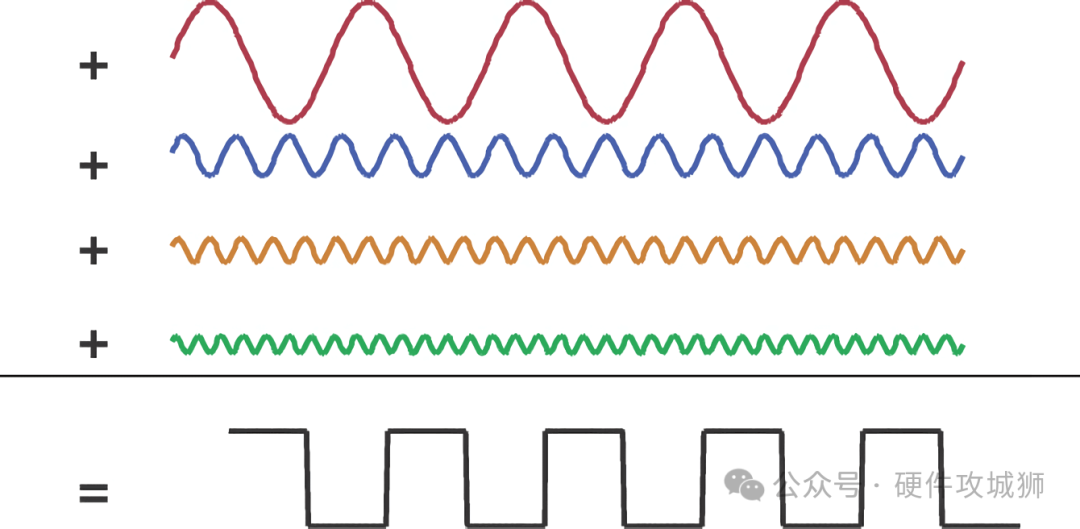
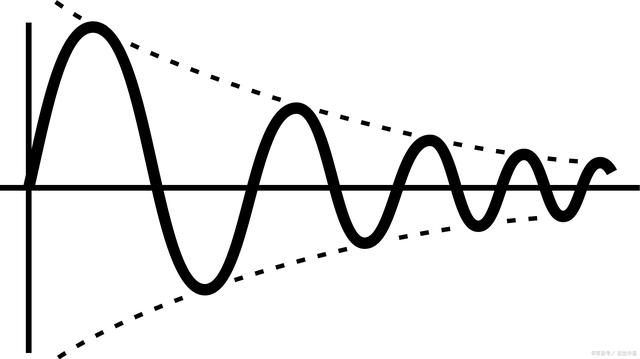
方波就是正弦波的多次諧波分量疊加,疊加次數越多,上升沿越陡,越接近于理想方波:

帶寬與上升沿
帶寬表示頻譜中最高有效正弦波頻率分量值(因為在數字信號中,最低頻永遠是直流),表示信號頻譜中的頻率范圍。帶寬的選擇對時域波形的最短上升沿有直接的影響。以理想方波為例,帶寬越大,上升沿就會越短,波形就越接近理想方波。
注意,「有效」表示信號諧波幅度高于相同基頻理想方波中對應諧波幅度的 70%。
例如,如果只用第 0、1、3 次諧波合成時域波形,那么波形的帶寬為第 3 次諧波的值即 3GHz。
根據實驗得出的經驗法則,帶寬與上升沿的關系為BW=0.35RT,其中 BW 為帶寬(GHz),RT 為 10%-90% 上升沿(ns)。舉個例子,如果信號的上升沿為 0.1ns,那么信號的帶寬就是 0.35GHz,反之也成立。(注意單位對應,GHz 對應 ns,MHz 對應 us)
-
信號
+關注
關注
11文章
2803瀏覽量
76980 -
時域
+關注
關注
1文章
72瀏覽量
28550 -
頻域
+關注
關注
1文章
89瀏覽量
26325
原文標題:信號完整性 - 時域與頻域
文章出處:【微信號:mcu168,微信公眾號:硬件攻城獅】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 從時域和頻域兩個角度對信號進行分析
從時域和頻域兩個角度對信號進行分析

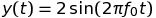












評論