濾波器一般用低通原型進(jìn)行描述,因?yàn)榈屯ㄊ菢?biāo)準(zhǔn)配置。如何將低通極點(diǎn)轉(zhuǎn)換成高通極點(diǎn)?ADI為你提供了一種轉(zhuǎn)換算法。速速 get 起來~
受原點(diǎn)零值的影響,其直流響應(yīng)并不平坦,而是n ×(20 dB/十倍頻程)的上升響應(yīng),其中n為極點(diǎn)數(shù)。在轉(zhuǎn)折頻率條件下,受極點(diǎn)影響,上述上升響應(yīng)會(huì)增加n × (–20 dB/十倍頻程)的響應(yīng)。結(jié)果是,在轉(zhuǎn)折頻率以外,會(huì)呈現(xiàn)平坦的響應(yīng)。
以1/s縮放傳遞函數(shù),可將低通原型轉(zhuǎn)換成高通濾波器。實(shí)際上,這通常相當(dāng)于將電容變成值為1/C的電感,而對于無源設(shè)計(jì),則相當(dāng)于將電感變成值為1/L的電容。對于有源設(shè)計(jì),電阻變成值為1/R的電容,而電容則變成值為1/C的電阻。這僅適用于頻率設(shè)置電阻,不適用于增益設(shè)置電阻(即并非適用于電路中的每個(gè)電阻或電容)。
考察轉(zhuǎn)換的另一種方式是研究s平面的轉(zhuǎn)換。低通原型的復(fù)數(shù)極點(diǎn)對由一個(gè)實(shí)部α和一個(gè)虛部β構(gòu)成。歸一化高通極點(diǎn)通過以下公式算出

以及

這樣,一個(gè)簡單的極點(diǎn)α0轉(zhuǎn)換成

低通零點(diǎn)(ωZ,LP)通過以下公式轉(zhuǎn)換

此外,原點(diǎn)處將增加與極點(diǎn)數(shù)量相等的零點(diǎn)。
在將歸一化低通原型極點(diǎn)和零點(diǎn)轉(zhuǎn)換成高通之后,接著以與低通相同的方式(即以頻率和阻抗)進(jìn)行反向歸一化處理。
作為例子,此處轉(zhuǎn)換的是一個(gè)1 kHz、3極點(diǎn)、0.5 dB切比雪夫?yàn)V波器。選擇切比雪夫?yàn)V波器的原因在于,如果響應(yīng)不正確,它可以更清楚地顯示出來;這種情況下,巴特沃茲則可能過于寬松。選擇3極點(diǎn)濾波器是為了分別轉(zhuǎn)換一個(gè)極點(diǎn)對和單個(gè)極點(diǎn)。
極點(diǎn)位置
低通原型的極點(diǎn)位置來自設(shè)計(jì)表。
表1

第一級為極點(diǎn)對,第二級為單極點(diǎn)。請注意,用α表示兩個(gè)完全不同的參數(shù)的做法是不可取的。左側(cè)的α和β為復(fù)平面上的極點(diǎn)位置。這些是轉(zhuǎn)換算法中使用的值。右側(cè)的α為1/Q,這正是物理濾波器設(shè)計(jì)等式所希望看到的。轉(zhuǎn)換結(jié)果將產(chǎn)生如表2所示結(jié)果。
表2

這里需要提醒一下,由于描述切比雪夫?yàn)V波器的一種習(xí)慣做法(即此處所用做法)是引用誤差帶的末端而非3 dB頻率,因此,F(xiàn)0必須除以(高通)紋波帶與3 dB帶寬的比值。
用Sallen-Key高通拓?fù)浣Y(jié)構(gòu)來構(gòu)建濾波器,原理圖見圖1。

圖1. 高通轉(zhuǎn)換
圖2所示為低通原型和高通轉(zhuǎn)換的響應(yīng)。請注意,它們在1 kHz截止頻率左右是對稱的。還應(yīng)注意,0.5 dB誤差帶位于1 kHz,而不是?3 dB點(diǎn),這是切比雪夫?yàn)V波器的一個(gè)特征。響應(yīng)的對稱性驗(yàn)證了轉(zhuǎn)換的精度。
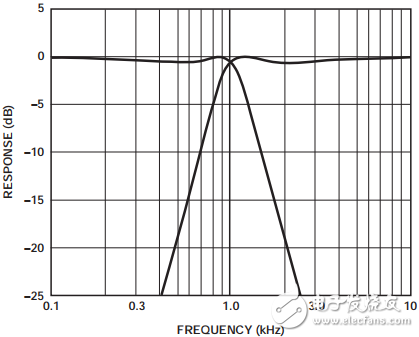
圖2. 低通和高通響應(yīng)
從低通到高通濾波器的轉(zhuǎn)換,上述算法你get到了么?
-
濾波器
+關(guān)注
關(guān)注
161文章
7953瀏覽量
179948 -
算法
+關(guān)注
關(guān)注
23文章
4660瀏覽量
94003
原文標(biāo)題:一種算法,實(shí)現(xiàn)濾波器的低通到高通轉(zhuǎn)換
文章出處:【微信號(hào):analog_devices,微信公眾號(hào):analog_devices】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
轉(zhuǎn)換測量卡爾曼濾波器設(shè)計(jì)與實(shí)現(xiàn)-- 其中的 “轉(zhuǎn)換測量“...
帶通濾波器與低通+高通結(jié)合的區(qū)別??
如何設(shè)計(jì)低通FIR濾波器
如何實(shí)現(xiàn)低和使用濾波器2.20高通濾波組件?
一種基于分布式算法的低通FIR濾波器
低通模擬濾波器的重要設(shè)計(jì)淺析
LMS自適應(yīng)濾波器的算法原理和應(yīng)該如何實(shí)現(xiàn)
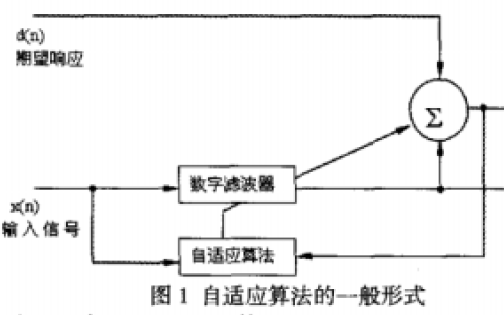
從低通到帶通濾波器的轉(zhuǎn)換

數(shù)字濾波器是什么 數(shù)字濾波器的性能指標(biāo)
數(shù)字信號(hào)處理基礎(chǔ)之時(shí)頻轉(zhuǎn)換和濾波器設(shè)計(jì)


















評論