一、濾波的概念

濾波是指通過某種方法將信號中的某些頻率成分增強或抑制，達到去除噪聲、改善信號質量、分離信號等目的的過程。濾波器是實現濾波功能的關鍵組件，它可以改變信號的頻譜特性，對不同頻率區(qū)域的信號進行處理。

二、常見的濾波算法

1.小波變換濾波

原理：小波變換通過將信號分解成不同尺度的子信號，可以提取出信號中的局部特征。在濾波中，小波變換可以用來去除信號中的噪聲或者對信號進行平滑處理。

下面是該算法的波形圖：

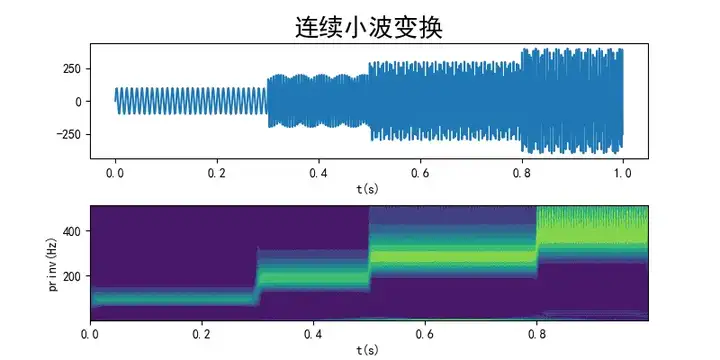
使用場景：

（1）圖像去噪：小波變換可以有效地去除圖像中的噪聲，尤其是在多尺度分解中，可以針對不同頻率的噪聲進行過濾。

（2）特征提取：小波變換能夠揭示圖像或信號中的局部特征，因此在特征提取方面非常有用，比如在圖像識別和分類中。

（3）邊緣檢測：小波變換在邊緣檢測方面表現出色，因為它能夠捕捉到圖像中的尖銳變化。

（4）信號去噪：在信號處理中，小波變換可以用于去除信號中的噪聲，尤其是在非平穩(wěn)信號中。

2.移動平均濾波

原理：首先確定一個包含一定數量樣本點的窗口，這個窗口在信號上滑動。在每一個位置，計算窗口內所有樣本點的平均值。將計算得到的平均值作為濾波后的輸出。將窗口沿信號滑動一定步長，重復上述步驟。

我們有一個離散時間信號 x[n]，并且我們使用長度為 M 的窗口進行移動平均濾波，那么濾波后的信號 y[n] 可以通過以下公式計算：則計算公式為：

y[n]=1/M∑k=n?M+1nx[k]

例如：一個包含噪聲的信號序列x=[1,4,3,6,6,5,10,9,7,12].

我們可以使用移動平均濾波來平滑信號并減小噪聲的影響。假設我們選擇一個窗口大小為3，即每次計算三個樣本的平均值。

第一個輸出樣本為：y[0]=(1/3)?(1+4+3)=2.666

第二個輸出樣本為：y[1]=(1/3)?(4+3+6)=4.33

以此類推，我們可以繼續(xù)計算后續(xù)輸出樣本。

下面是使用這個算法生成的一個波形圖

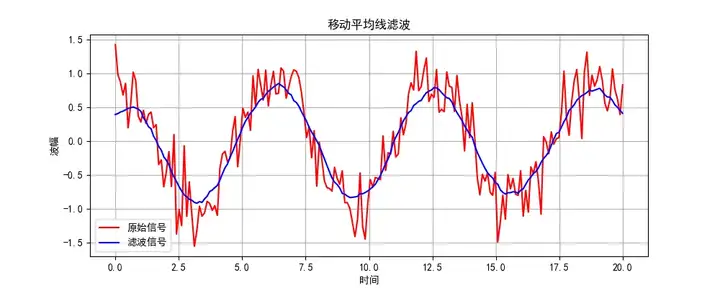
使用場景：

（1）在金融領域等需要對數據進行趨勢分析的場景中，移動平均濾波可以平滑價格波動，幫助分析數據的長期趨勢，預測未來走勢。

（2）在實時數據處理或傳感器數據處理中，移動平均濾波可以利用先前時刻的數據進行濾波處理，對新的數據進行平均，有助于消除數據中的噪聲或異常值。

（3）移動平均濾波對周期性噪聲和高頻噪聲的濾波效果比較好，可以很好地降低信號或數據中的高頻成分，同時保留信號的基本特征。

3.中值濾波

原理：中值濾波會選取數字圖像或數字序列中像素點及其周圍臨近像素點（一共有奇數個像素點）的像素值，將這些像素值排序，然后將位于中間位置的像素值作為當前像素點的像素值，讓周圍的像素值接近真實值，從而消除孤立的噪聲點。例如，針對下圖中第4行第3列的像素點，計算它的中值濾波值。

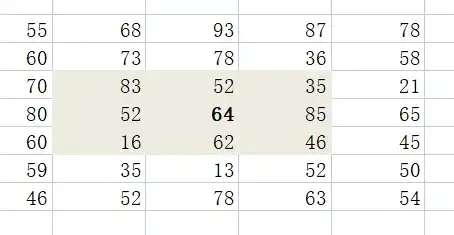
將其鄰域設置為3×3大小，對其3×3鄰域內像素點的像素值進行排序（升序降序均可），按升序排序后得到序列值為：[16，35，46，52，52，62，64，83，85]，在該序列中，處于中心位置（也叫中心點或中值點）的值是“52”，因此用該值替換原來的像素值 64，作為當前點的新像素值，新的像素圖如下所示。

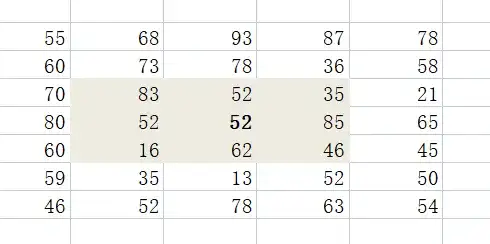
下面是使用這個算法對隨機噪聲濾波后生成的一個波形圖：

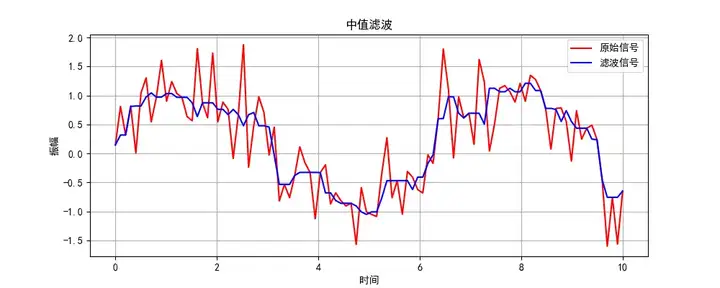
使用場景：

（1）孤立噪聲點平滑：中值濾波能有效去除圖像或信號中的孤立噪聲點，而不會對整體圖像或信號的平滑區(qū)域造成影響。

（2）椒鹽噪聲去除：中值濾波對椒鹽噪聲（salt-and-pepper noise）具有很好的濾除效果，這種噪聲表現為圖像中隨機分布的白色和黑色像素點。

（3）實時視頻處理：由于中值濾波算法的計算復雜度相對較低，它可以用于實時視頻流的噪聲去除。

4.算術平均濾波

原理：算術平均濾波是圖像處理中的一個常用技術，主要用于降低圖像中的隨機噪聲。算術平均濾波器的基本思想是用像素點鄰域內的平均灰度值來代替該像素點的灰度值。

算術平均濾波的計算公式如下：

f'(x, y) = 1/(mn) * ΣΣf(x+k, y+l)

其中，f'(x, y)是濾波后像素點(x, y)的灰度值，f(x+k, y+l)是原像素點(x, y)領域內的灰度值，ΣΣ表示對領域內所有像素點求和，m和n是濾波窗口的大小。

下面是使用這個算法對隨機噪聲濾波后生成的一個波形圖：

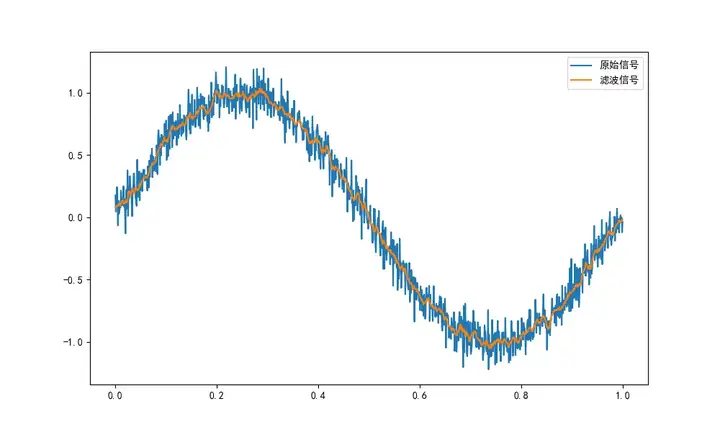
算術平均濾波適用于一些簡單的圖像或信號處理場景，例如去除較為均勻且較弱的噪聲。

5.卡爾曼濾波

原理：

（1）預測步驟（預測狀態(tài)）：通過系統(tǒng)的動態(tài)模型，根據已知的系統(tǒng)狀態(tài)和控制量，預測系統(tǒng)的下一個狀態(tài)以及狀態(tài)的協(xié)方差。這一步驟得到的是對系統(tǒng)未來狀態(tài)的預測。

（2）測量更新步驟（更新狀態(tài)）：利用傳感器測量數據，根據預測的狀態(tài)和測量數據的協(xié)方差，通過卡爾曼增益計算得到關于系統(tǒng)狀態(tài)的修正估計。卡爾曼增益會根據預測和測量的不確定性來調整估計值，以平衡兩者之間的權重。

下面是使用這個算法對隨機噪聲濾波后生成的一個波形圖：

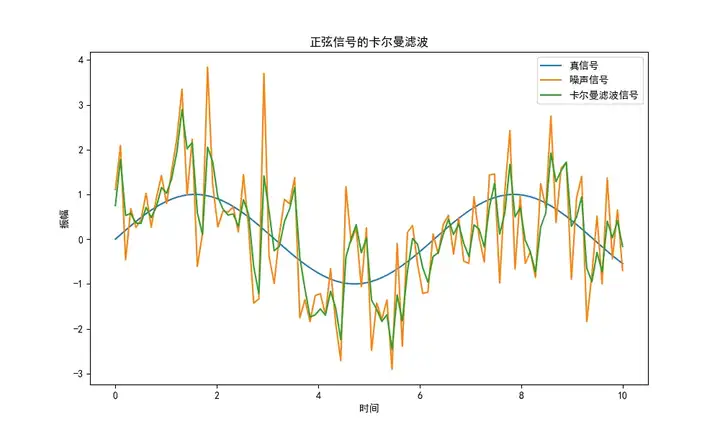
使用場景：卡爾曼濾波廣泛應用于估計動態(tài)系統(tǒng)的狀態(tài)，例如航天器導航、飛行器控制、傳感器數據融合等領域。它具有高效、準確、穩(wěn)定等優(yōu)點，能夠處理系統(tǒng)模型不確定性、傳感器誤差等問題，提高狀態(tài)估計的精度和魯棒性。

6.均值濾波

原理：連續(xù)采樣N個數據，去掉一個最大值和一個最小值然后計算N-2個數據的算術平均值N值的選取

下面是使用這個算法對隨機噪聲濾波后生成的一個波形圖：

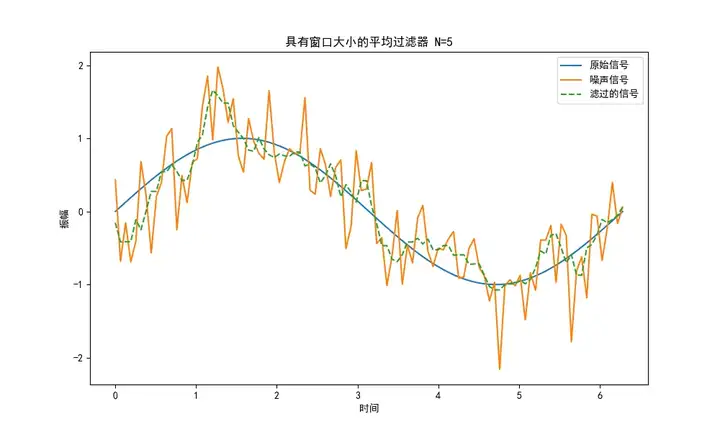
使用場景：
（1）工業(yè)自動化：在工業(yè)自動化和控制系統(tǒng)中，均值濾波用于從傳感器數據中去除噪聲，提高系統(tǒng)的穩(wěn)定性和可靠性。

（2）信號平滑：當信號受到高頻干擾或隨機噪聲時，中值平均濾波法可以將突然的干擾降低，使信號變得更加平滑。

（3）環(huán)境監(jiān)測：在環(huán)境監(jiān)測中，均值濾波可以用于處理大氣、水質等監(jiān)測數據，去除測量誤差和隨機波動。

（4）數字圖像處理：在數字圖像處理中，中值平均濾波法常用于去除圖像中的噪聲，例如在數字攝影中去除低光照條件下的圖像噪聲。

7.快速傅里葉變換（FFT）濾波

原理：FFT濾波將時域信號通過FFT算法轉換到頻域，得到信號在頻域上的頻譜信息。在頻域上對信號進行濾波處理，可以采用各種濾波器，如低通濾波器、高通濾波器、帶通濾波器等，以抑制或增強特定頻率成分。對經過濾波處理的頻域信號進行逆FFT，將信號恢復回時域。

我使用python生成了一個頻率為50 Hz的正弦波信號，并添加了高斯噪聲。然后，使用numpy.fft.fft函數計算信號的FFT，并使用numpy.fft.fftfreq生成對應的頻率向量。接下來，設計了一個簡單的低通濾波器，只允許截止頻率以下的頻率成分通過。應用濾波器后，使用numpy.fft.ifft計算逆FFT，得到濾波后的信號。

下面是濾波的效果圖：

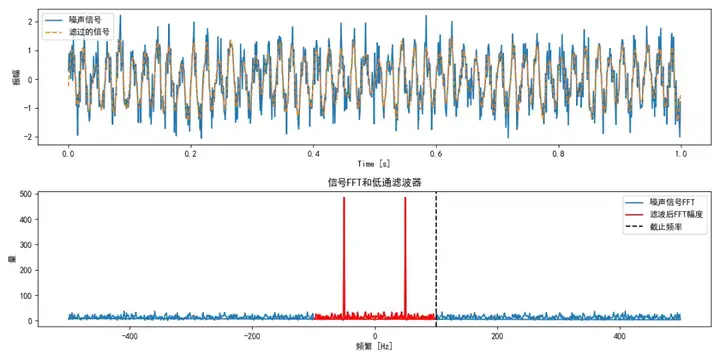
使用場景：

（1）頻域濾波：FFT允許將時域信號轉換到頻域，然后可以輕松地應用各種濾波器，如低通、高通、帶通和帶阻濾波器。

（2）信號分析：FFT常用于分析信號的頻率成分，識別信號中的周期性成分或檢測特定頻率的信號。

（3）圖像處理：在圖像處理中，FFT可以用于頻域濾波，如銳化、模糊、邊緣檢測等。

審核編輯 黃宇