支路電流法(Node Voltage Method)是一種在電路分析中常用的方法,主要用于求解線性電路中的電流和電壓。然而,對于非線性電路,支路電流法的應用會受到一定的限制。
- 支路電流法的基本原理
支路電流法是一種基于基爾霍夫電流定律(KCL)的電路分析方法。基爾霍夫電流定律指出,在一個電路節點上,流入節點的電流之和等于流出節點的電流之和。通過將電路分解為若干個支路,并在每個節點上應用基爾霍夫電流定律,可以列出一組線性方程組,進而求解電路中的電流和電壓。
- 非線性電路的特點
非線性電路是指電路元件的電壓-電流關系不是線性的,即元件的電阻、電容或電感等參數與電流或電壓的關系不是簡單的正比關系。常見的非線性元件包括二極管、晶體管、運算放大器等。非線性電路的特點是:
- 電壓-電流關系復雜,可能具有非線性、非對稱性或非單調性等特點。
- 電路的穩態和瞬態響應可能具有非線性特性,如諧振、振蕩等。
- 電路的分析和設計更加復雜,需要考慮非線性元件的非線性特性。
- 支路電流法在非線性電路中的應用
雖然支路電流法主要用于線性電路的分析,但在某些情況下,也可以應用于非線性電路的分析。以下是一些可能的應用場景:
3.1 線性化處理
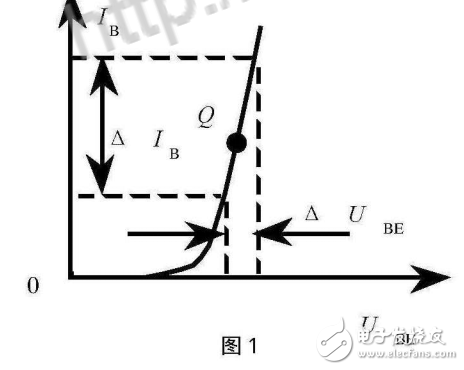
對于某些非線性元件,可以通過線性化處理將其轉化為線性元件。例如,對于二極管,可以在其工作點附近進行泰勒展開,保留一階項,忽略高階項,從而將其視為線性元件。然而,這種方法只適用于元件工作在近似線性的區域,對于大信號或強非線性元件,線性化處理可能不夠準確。
3.2 小信號分析
對于非線性電路,可以采用小信號分析的方法,即在電路的穩態工作點附近進行線性化處理,分析電路的小信號響應。這種方法適用于分析電路的穩定性、頻率響應等特性。然而,小信號分析無法反映電路的大信號行為和非線性特性。
3.3 迭代求解
對于復雜的非線性電路,可以采用迭代求解的方法。首先,假設電路中的非線性元件為線性元件,求解電路的初始解。然后,根據初始解計算非線性元件的實際工作狀態,更新電路的參數。重復這個過程,直到滿足一定的收斂條件。這種方法可以求解非線性電路的穩態和瞬態響應,但計算過程可能較為復雜。
- 支路電流法在非線性電路分析中的挑戰
盡管支路電流法在某些情況下可以應用于非線性電路的分析,但在實際應用中,仍然面臨一些挑戰:
4.1 非線性元件的建模難度
非線性元件的電壓-電流關系復雜,難以用簡單的數學模型描述。對于強非線性元件,如二極管、晶體管等,需要采用更復雜的模型,如二極管方程、Ebers-Moll模型等,這增加了電路分析的難度。
4.2 非線性方程的求解難度
非線性電路的方程組可能具有多個解,甚至可能沒有解。求解非線性方程組需要采用特殊的數值方法,如牛頓法、擬牛頓法等,這些方法的計算復雜度較高,收斂速度可能較慢。
4.3 穩定性和收斂性問題
在非線性電路的分析過程中,可能遇到穩定性和收斂性問題。例如,在迭代求解過程中,可能存在多個穩定點,導致求解過程陷入局部最優解。此外,非線性電路的瞬態響應可能具有振蕩、混沌等復雜現象,增加了分析的難度。
- 解決方案
針對支路電流法在非線性電路分析中遇到的挑戰,可以采取以下解決方案:
5.1 選擇合適的非線性模型
根據非線性元件的特性和電路的工作條件,選擇合適的非線性模型。對于簡單的非線性元件,可以采用線性化處理或小信號分析;對于復雜的非線性元件,需要采用更精確的非線性模型。
5.2 采用高效的數值方法
在求解非線性方程組時,可以采用高效的數值方法,如牛頓法、擬牛頓法等。這些方法可以提高求解速度,提高收斂性。同時,可以采用多尺度方法、同倫方法等,以提高求解的穩定性和準確性。
5.3 引入輔助變量和約束條件
在非線性電路的分析過程中,可以引入輔助變量和約束條件,以簡化問題。例如,可以引入電流源、電壓源等輔助元件,將非線性電路轉化為線性電路;或者引入功率平衡、能量守恒等約束條件,以限制電路的工作狀態。
-
電感
+關注
關注
54文章
6153瀏覽量
102601 -
非線性電路
+關注
關注
0文章
15瀏覽量
6173 -
基爾霍夫電流定律
+關注
關注
2文章
27瀏覽量
8179 -
支路電流法
+關注
關注
0文章
18瀏覽量
6778
發布評論請先 登錄
相關推薦
非線性電路的分析方法_非線性電路分析舉例




 支路電流法適用于非線性電路嗎
支路電流法適用于非線性電路嗎










評論