在信號處理領域,濾波器是一種非常重要的工具,用于對信號進行處理,以去除噪聲、提取有用信息或實現其他特定功能。濾波器的類型有很多,如低通濾波器、高通濾波器、帶通濾波器、帶阻濾波器等。正確地選擇和使用濾波器對于信號處理的質量至關重要。
- 引言
濾波器是一種對信號進行頻率選擇的系統,其核心功能是通過特定的數學模型對信號進行處理,以實現對信號的濾波。濾波器的類型主要取決于其頻率響應特性,即濾波器對不同頻率成分的響應程度。在實際應用中,根據信號的特點和處理需求,選擇合適的濾波器類型是非常重要的。
1.1 濾波器的基本概念
濾波器是一種線性時不變(LTI)系統,其輸入和輸出之間的關系可以通過系統函數(也稱為傳遞函數)來描述。系統函數是一個復數函數,表示濾波器對不同頻率成分的響應。通過分析系統函數,我們可以了解濾波器的頻率響應特性,從而判斷其類型。
1.2 濾波器的分類
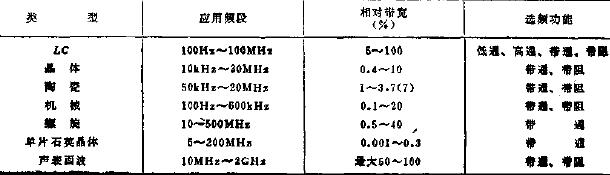
濾波器按照其頻率響應特性可以分為以下幾類:
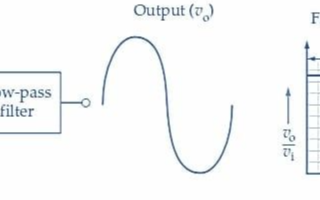
- 低通濾波器(Low-Pass Filter, LPF):允許低頻信號通過,抑制高頻信號。
- 高通濾波器(High-Pass Filter, HPF):允許高頻信號通過,抑制低頻信號。
- 帶通濾波器(Band-Pass Filter, BPF):允許特定頻率范圍內的信號通過,抑制其他頻率的信號。
- 帶阻濾波器(Band-Stop Filter, BSF):抑制特定頻率范圍內的信號,允許其他頻率的信號通過。
- 全通濾波器(All-Pass Filter, APF):對所有頻率的信號都具有相同的增益,但會改變信號的相位。
1.3 系統函數與濾波器類型的關系
系統函數是描述濾波器輸入和輸出之間關系的數學模型。通過分析系統函數,我們可以了解濾波器的頻率響應特性,從而判斷其類型。系統函數通常表示為:
H(s) = Y(s) / X(s)
其中,H(s)是系統函數,Y(s)是濾波器的輸出信號的拉普拉斯變換,X(s)是濾波器的輸入信號的拉普拉斯變換。
- 系統函數的表示方法
系統函數可以通過不同的數學工具來表示,如多項式、有理函數、部分分式等。在實際應用中,我們通常使用復數域的方法來分析系統函數,以便更好地理解濾波器的頻率響應特性。
2.1 多項式表示法
多項式表示法是最基本的系統函數表示方法,通常用于描述線性時不變系統。在這種表示法中,系統函數可以表示為:
H(s) = b_m * s^m + b_(m-1) * s^(m-1) + ... + b_1 * s + b_0
/ a_n * s^n + a_(n-1) * s^(n-1) + ... + a_1 * s + a_0
其中,b_m、b_(m-1)、...、b_0是分子的系數,a_n、a_(n-1)、...、a_0是分母的系數,s是拉普拉斯變換中的復變量。
2.2 有理函數表示法
有理函數表示法是一種更通用的系統函數表示方法,可以用于描述線性時不變系統和某些非線性系統。在這種表示法中,系統函數可以表示為:
H(s) = N(s) / D(s)
其中,N(s)是分子多項式,D(s)是分母多項式。
2.3 部分分式表示法
部分分式表示法是一種特殊的有理函數表示法,用于將系統函數分解為若干個簡單的部分分式。這種表示法有助于我們更容易地分析系統函數的頻率響應特性。部分分式表示法通常表示為:
H(s) = c_1 / (s - z_1) + c_2 / (s - z_2) + ... + c_k / (s - z_k)
其中,c_1、c_2、...、c_k是常數,z_1、z_2、...、z_k是部分分式的極點。
-
濾波器
+關注
關注
161文章
7859瀏覽量
178694 -
頻率
+關注
關注
4文章
1534瀏覽量
59324 -
函數
+關注
關注
3文章
4345瀏覽量
62874 -
數學模型
+關注
關注
0文章
83瀏覽量
11966
發布評論請先 登錄
相關推薦
基于橢圓函數的LC帶通濾波器設計與仿真





 如何通過系統函數判斷濾波器類型
如何通過系統函數判斷濾波器類型










評論