異步計數(shù)器可以有 2 n -1 種可能的計數(shù)狀態(tài),例如 4 位計數(shù)器的 MOD-16(0-15),這使其非常適合用于頻分應用。但也可以使用基本異步計數(shù)器配置來構建計數(shù)狀態(tài)小于其最大輸出數(shù)的特殊計數(shù)器。例如,模數(shù)或 MOD 計數(shù)器。
這是通過強制計數(shù)器在預定值時將其自身重置為零來實現(xiàn)的,從而產(chǎn)生一種具有截斷序列的異步計數(shù)器。然后,計數(shù)到其最大模數(shù)(2 n )的n 位計數(shù)器稱為全序列計數(shù)器,而模數(shù)小于最大模數(shù)的 n 位計數(shù)器稱為截斷計數(shù)器。
但是,為什么我們要創(chuàng)建一個異步截斷計數(shù)器,而不是 MOD-4、MOD-8 或其他等于 2 的冪的模數(shù)呢?答案是,我們可以通過使用組合邏輯來利用觸發(fā)器上的異步輸入。
如果我們采用模 16 異步計數(shù)器并用附加邏輯門對其進行修改,則可以使其提供十進制(除以 10)計數(shù)器輸出,以用于標準十進制計數(shù)和算術電路。
這種計數(shù)器通常稱為十進制計數(shù)器。十進制計數(shù)器需要在輸出計數(shù)達到十進制值 10 時(即 DCBA = 1010)重置為零,為此,我們需要將此條件反饋給重置輸入。計數(shù)序列從二進制“0000”(BCD =“0”)到“1001”(BCD =“9”)的計數(shù)器通常稱為 BCD 二進制編碼十進制計數(shù)器,因為其十狀態(tài)序列是 BCD 碼的序列,但二進制十進制計數(shù)器更常見。
異步十進制計數(shù)器
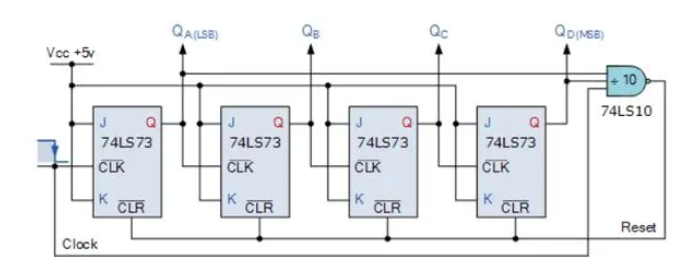
這種異步計數(shù)器在輸入時鐘信號的每個后沿從 0000 開始向上計數(shù),直到達到輸出 1001(十進制 9)。輸出 QA 和 QD 現(xiàn)在都等于邏輯“1”。在下一個時鐘脈沖施加時,74LS10 NAND 門的輸出狀態(tài)從邏輯“1”變?yōu)檫壿嫛?”電平。
由于 NAND 門的輸出連接到 所有 74LS73 JK 觸發(fā)器的CLEAR ( CLR ) 輸入,該信號導致所有Q輸出在計數(shù)為 10 時重置回二進制0000。由于輸出QA和QD現(xiàn)在都等于邏輯“0”(因為觸發(fā)器剛剛重置),NAND門的輸出返回到邏輯電平“1”,計數(shù)器再次從0000重新啟動。我們現(xiàn)在有一個十進制或模 10 遞增計數(shù)器。
十年計數(shù)器真值表
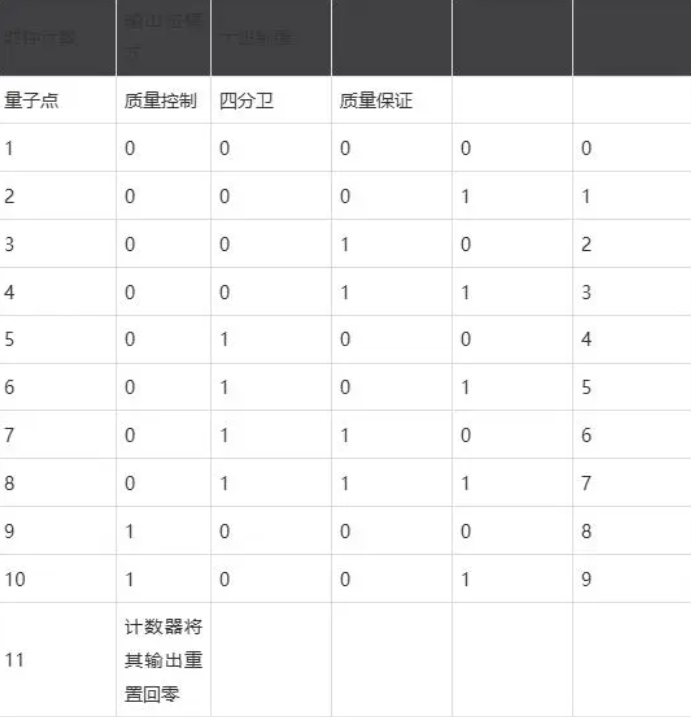
十進制計數(shù)器時序圖
通過使用截斷計數(shù)器輸出序列的相同想法,上述電路可以輕松地適應其他計數(shù)周期,只需改變與NAND門輸入的連接或使用其他邏輯門組合即可。
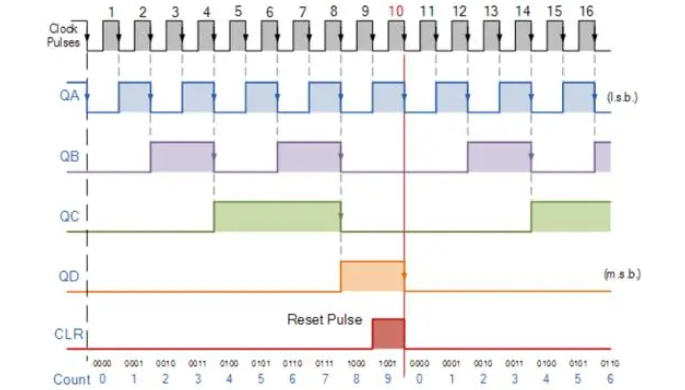
舉例來說,只需將“ QC ”和“ QD ”的輸出輸入到NAND門,就可以輕松實現(xiàn)十二進制(模 12) ,注意 12 的二進制等價物是1100,而輸出“ QA ”是最低有效位 (LSB)。
由于用n 個觸發(fā)器可實現(xiàn)的最大模數(shù)為2 n,這意味著在設計截斷異步計數(shù)器時,您應該確定大于或等于所需模數(shù)的最低 2 的冪。
假設我們希望從 0 數(shù)到 39,或者對 40 取模并重復。那么所需的觸發(fā)器數(shù)量最多為 6 個,n = 6可得到最大 MOD 為 64,因為 5 個觸發(fā)器是不夠的,因為這只能得到 MOD-32。
現(xiàn)在假設我們想構建一個“除以 128”的計數(shù)器用于分頻,我們需要級聯(lián)七個觸發(fā)器,因為 128 = 2 7。使用諸如 74LS74 之類的雙觸發(fā)器,我們?nèi)匀恍枰膫€ IC 來完成電路。
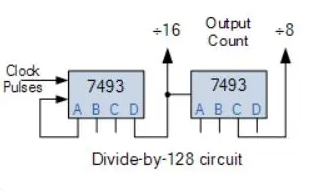
一種簡單的替代方法是使用兩個 TTL 7493 作為 4 位波紋計數(shù)器/分頻器。由于 128 = 16 x 8,因此可以將一個 7493 配置為“除以 16”計數(shù)器,將另一個配置為“除以 8”計數(shù)器。兩個 IC 可以級聯(lián)在一起,形成一個“除以 128”分頻器,如圖所示。
當然,也有標準 IC 異步計數(shù)器可用,例如 TTL 74LS90 可編程紋波計數(shù)器/分頻器,可配置為 2 分頻、5 分頻或兩者的任意組合。74LS390 是一種非常靈活的雙十進制驅(qū)動器 IC,具有大量可用的“分頻”組合,包括 2 分頻、4 分頻、5 分頻、10 分頻、20 分頻、25 分頻、50 分頻和 100 分頻。
分頻器
紋波計數(shù)器能夠截斷序列以產(chǎn)生“除以 n”的輸出,這意味著計數(shù)器(尤其是紋波計數(shù)器)可用作分頻器,以將高時鐘頻率降低到更可用的值,以用于數(shù)字時鐘和計時應用。例如,假設我們需要一個精確的 1Hz 計時信號來操作數(shù)字時鐘。
我們可以很容易地使用配置為非穩(wěn)態(tài)多諧振蕩器的標準 555 定時器芯片產(chǎn)生 1Hz 方波信號,但制造商的數(shù)據(jù)表告訴我們,555 定時器根據(jù)制造商的不同,通常具有 1-2% 的定時誤差,并且在 1Hz 的低頻下,這個 2% 的定時誤差是不好的。
但是,數(shù)據(jù)表還告訴我們,555 定時器的最大工作頻率約為 300kHz,在此高頻率下 2% 的誤差(雖然在最大約 6kHz 時仍然很大)是可以接受的。因此,通過選擇更高的定時頻率(例如 262.144kHz)和 18 位波紋(Modulo-18)計數(shù)器,我們可以輕松制作出精度為 1Hz 的定時信號,如下所示。
來自 18 位異步波紋計數(shù)器的 1Hz 定時信號
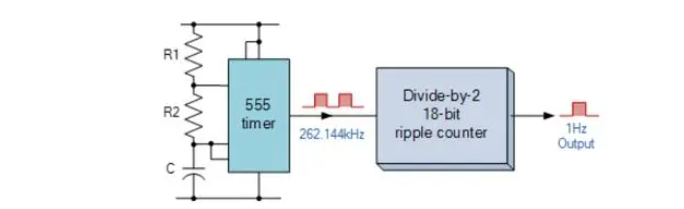
這當然是一個非常簡單的如何產(chǎn)生精確定時頻率的例子,但通過使用高頻晶體振蕩器和多位分頻器,可以為從時鐘或手表到事件定時甚至電子鋼琴/合成器或音樂類型應用等各種應用產(chǎn)生精密頻率發(fā)生器。
不幸的是,異步計數(shù)器的主要缺點之一是由于門的內(nèi)部電路,時鐘脈沖到達其輸入端和出現(xiàn)在其輸出端之間存在微小的延遲。
在異步電路中,這種延遲稱為傳播延遲,因此異步紋波計數(shù)器有“傳播計數(shù)器”的綽號,在某些高頻情況下,這種延遲會產(chǎn)生錯誤的輸出計數(shù)。
在大位波紋計數(shù)器電路中,如果將各個階段的延遲全部加在一起,在計數(shù)器鏈的末端產(chǎn)生總延遲,則輸入信號和計數(shù)輸出信號之間的時間差可能非常大。這就是為什么異步計數(shù)器通常不用于涉及大量位的高頻計數(shù)電路的原因。
此外,計數(shù)器的輸出彼此之間沒有固定的時間關系,并且由于它們的時鐘序列,它們不會在同一時刻發(fā)生。換句話說,輸出頻率逐一可用,這是一種多米諾骨牌效應。然后,添加到異步計數(shù)器鏈的觸發(fā)器越多,最大工作頻率就越低,以確保準確計數(shù)。為了克服傳播延遲問題,開發(fā)了同步計數(shù)器。
然后總結一下異步計數(shù)器的一些優(yōu)點:
異步計數(shù)器可以很容易地由切換觸發(fā)器或 D 型觸發(fā)器制成。
它們被稱為“異步計數(shù)器”,因為觸發(fā)器的時鐘輸入并非全部由相同的時鐘信號驅(qū)動。
鏈中的每個輸出都取決于前一個觸發(fā)器輸出的狀態(tài)變化。
異步計數(shù)器有時也稱為波紋計數(shù)器,因為數(shù)據(jù)似乎從一個觸發(fā)器的輸出“波紋”到下一個觸發(fā)器的輸入。
它們可以使用“除以 n”計數(shù)器電路來實現(xiàn)。
截斷計數(shù)器可以產(chǎn)生任意模數(shù)計數(shù)。
異步計數(shù)器的缺點:
可能需要額外的“重新同步”輸出觸發(fā)器。
要計算不等于2 n 的截斷序列,需要額外的反饋邏輯。
如果計算大量的位數(shù),則連續(xù)階段的傳播延遲可能會變得過大。
這種延遲使它們獲得了“傳播計數(shù)器”的綽號。
在高時鐘頻率下會發(fā)生計數(shù)錯誤。
同步計數(shù)器更快、更可靠,因為它們對所有觸發(fā)器使用相同的時鐘信號。
審核編輯 黃宇
-
觸發(fā)器
+關注
關注
14文章
2003瀏覽量
61290 -
異步計數(shù)器
+關注
關注
0文章
10瀏覽量
8070
發(fā)布評論請先 登錄
相關推薦
壓控振蕩器仿真原理是什么
壓控振蕩器vco工作原理是什么
壓控振蕩器芯片控制信號的原理
反饋式振蕩器的振蕩平衡條件是什么
振蕩器的工作原理、類型及設計方法
深入了解 MEMS 振蕩器 溫度補償 MEMS 振蕩器 TC-MO
反饋振蕩器的構成和工作原理
考畢茲振蕩器電路圖 考畢茲振蕩器的工作原理和特點
非穩(wěn)態(tài)多諧振蕩器與單穩(wěn)態(tài)多諧振蕩器電路詳解
什么是LC三端式振蕩器 LC三端式振蕩器工作原理




 了解反饋振蕩器,看這篇文章就夠了
了解反饋振蕩器,看這篇文章就夠了










評論