1 二項式分布推導計算
二項分布的推導過程主要基于組合數學和概率論的基本原理。假設有一個隨機試驗,每次試驗只有兩種可能的結果,通常稱為“成功”和“失敗”。成功的概率為p,失敗的概率為1?p。現在進行n次獨立重復試驗,在這n次試驗中成功k次的概率。
推導過程如下:
1) 確定組合方式:
首先,需要確定在n次試驗中成功k次的組合方式有多少種。這可以通過組合數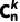 (也叫二項式系數)來計算,它表示從n個不同項中選取k個的不同方式的數目。組合數的計算公式為:
(也叫二項式系數)來計算,它表示從n個不同項中選取k個的不同方式的數目。組合數的計算公式為:
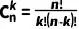 ??
??
(1)
其中n!表示n的階乘,即 n×(n?1)×…×2×1。
2) 計算每種組合方式的概率:
接下來,計算每一種組合方式對應的概率。由于每次試驗成功的概率是p,失敗的概率是1?p,且試驗是獨立的,所以成功k次且失敗n?k次的概率為pk×(1?p)n?k。
3) 將組合數與概率相乘:
最后,將組合數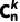 與每一種組合方式的概率pk×(1?p)n?k相乘,并考慮到所有可能的k值(從0到n),得到成功次數為k的總概率。因此,二項分布的概率質量函數為:
與每一種組合方式的概率pk×(1?p)n?k相乘,并考慮到所有可能的k值(從0到n),得到成功次數為k的總概率。因此,二項分布的概率質量函數為:
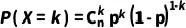 ????
????
k=0,1,2,…,n(2)
這個公式描述了在n次獨立重復試驗中成功次數為k的概率,即二項分布的概率質量函數。
需要注意的是,當n和k的值較大時,直接計算階乘和組合數可能會非常繁瑣。在實際應用中,通常會使用編程庫中的二項式分布函數來進行計算,這些函數已經優化了計算過程,可以高效地處理大數值的情況。
2 從二項分布到泊松分布推導計算
從二項式分布推導泊松分布的詳細計算過程涉及幾個關鍵步驟和近似。逐步推導:
首先,回顧二項式分布的概率質量函數:
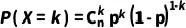 ????
????
k=0,1,2,…,n (3)
其中,X表示在n次獨立重復試驗中成功的次數,p是每次試驗成功的概率。
現在,考慮一種特殊情況:當n很大,p很小,但np保持為一個中等大小的常數時,二項式分布可以近似為泊松分布。
推導過程如下:
1) 使用斯特林公式近似階乘:
斯特林公式給出了階乘的一個近似表達式:
 ?????????????
?????????????
(4)
e是自然對數的底數,約等于 2.71828。
利用這個公式,我們可以近似計算組合數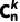 : ? ?
: ? ?
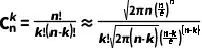 ???????
???????
(5)
簡化后得到:
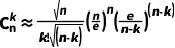 ??????
??????
(6)
2) 將p替換為λ/n:
在泊松分布的上下文中,我們通常使用參數λ來表示平均發生率或期望值,即λ=np。因此,可以將p替換為λ/n得到
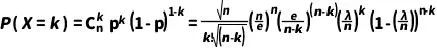 ?????
?????
(7)
進一步簡化,考慮到n很大而k相對較小,并且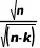 ?的影響在?n?很大時可以忽略。
?的影響在?n?很大時可以忽略。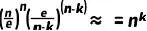 。
。
上式子簡化為
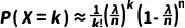 ????
????
(8)
根據指數函數的性質
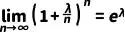 ??????
??????
(9)
3) 當n趨于無窮大時,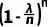 ?趨近于?
?趨近于?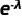 (這是由指數函數的定義和性質得出的)。因此,上述(8)式進一步簡化為:
(這是由指數函數的定義和性質得出的)。因此,上述(8)式進一步簡化為:
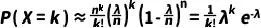 ?????
?????
(10)
這就是泊松分布的概率密度函數。綜上所述,當二項式分布中的試驗次數n很大,而每次試驗成功的概率p很小時,通過一系列近似和變換,我們可以將二項式分布近似為泊松分布。這種近似在統計學和概率論中非常有用,特別是在處理大量小概率事件時。
3 泊松分布在分子免疫檢測中的應用
在分子免疫檢測中,泊松分布可以用于描述在一定區域內(如細胞表面、組織切片等)隨機出現的抗原分子數量或者熒光標記分子的數量。例如:
1)流式細胞術分析
在流式細胞儀中,我們可能對單個細胞上特定抗原受體的數量感興趣。假設平均每個細胞上有 λ 個受體,那么根據泊松分布,給定細胞上具有 k 個受體的概率可以通過泊松概率質量函數來計算:

這有助于研究人員了解細胞群體中不同受體表達水平的細胞比例。
2)免疫組化或免疫熒光實驗:
在這些實驗中,抗體與組織切片上的靶蛋白結合后,通過顯色劑或熒光探針進行可視化。每單位面積(如一個視野或一個細胞核內)的陽性信號點數可以服從泊松分布。
實驗人員可能想要知道在一定的觀察窗口內觀測到 k 個信號點的概率,特別是在背景噪聲較高的情況下,泊松分布可以幫助量化這一隨機過程。
3)病毒或微生物計數:
分子免疫檢測也包括對病毒顆粒、細菌或其他微生物的定量。例如,在病毒載量檢測中,如果已知樣本中的平均病毒濃度,泊松分布可以用來預測在一次檢測中發現某個病毒拷貝數的概率。
4)基因表達定量:
在RNA測序(RNA-Seq)數據分析中,泊松分布模型有時也被用于估計轉錄本的豐度。盡管更為復雜的統計模型常被使用,但在某些簡化條件下,基因表達水平的變化可以近似為泊松過程。
通過泊松分布的建模和計算,研究者能夠更準確地推斷出生物分子的實際分布情況,并以此為基礎進行進一步的數據分析和統計推斷。
4 計算實例
泊松分布可以被用來精確描述超低濃度蛋白分子的檢測過程。以下是泊松分布在分子免疫檢測中的一個具體計算示例:
假設我們正在檢測一種特定蛋白質分子的濃度,其平均出現率為λ。為了簡化計算,我們假設λ=3,即平均每個樣本中有3個蛋白質分子。現在,我們想要計算在一個樣本中檢測到k個蛋白質分子的概率。這可以通過泊松分布的概率質量函數來完成。概率質量函數的公式為:

其中,X是觀察到的蛋白質分子數,k是具體的次數,λ是平均出現率。
例如,我們想要計算在一個樣本中檢測到恰好2個蛋白質分子的概率。將λ=3和k=2代入公式,我們得到:
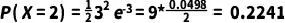
所以,在一個樣本中檢測到恰好2個蛋白質分子的概率約為0.2241。
假設在一項針對某種細胞表面抗原的流式細胞術實驗中,我們已知平均每個細胞上大約有4個該抗原分子(λ=4)。現在想要計算在給定的一個細胞上觀察到恰好有6個這種抗原分子的概率。
根據泊松分布的概率質量函數,可以這樣計算:

將 λ = 4 和 k = 6 帶入公式:
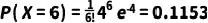
所以,在這個例子中,觀察到一個細胞上有6個該抗原分子的概率約為11.53%。
類似地,我們可以計算其他k值的概率。如果我們想要知道檢測到蛋白質分子數少于或等于某個特定值(比如3)的概率,我們可以計算所有小于或等于3的k值的概率,并將它們相加。這稱為累積分布函數。值得注意的是,由于泊松分布的前提是事件之間是相互獨立的,因此在實際應用中,需要確保樣本中的蛋白質分子是隨機分布的,且每個分子的檢測是獨立的。此外,λ的估計也是非常重要的,它可以通過實驗數據或理論模型來得出。通過這種方法,泊松分布在分子免疫檢測中為我們提供了一種精確量化超低濃度蛋白質分子的工具,對于生物醫學研究和臨床診斷等領域具有重要意義。
熒光分子計數中,泊松分布可以用于預測在某個區域內(如細胞內或顯微圖像的像素點)隨機出現熒光標記分子的數量。例如,在單分子熒光成像實驗中,我們對每個細胞內某種蛋白質分子的平均表達量為λ個。
假設研究者使用了熒光標記技術來檢測和量化細胞內的某種蛋白質,并且通過分析得知,在一個典型細胞內平均有100個這種熒光標記的蛋白質分子(即λ=100)。現在他們想要計算在一個特定細胞內恰好觀測到120個熒光信號的概率。
應用泊松分布概率質量函數:

將 λ = 100 和 k = 120 帶入公式:
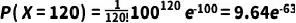
這個結果非常小,表示在給定條件下,觀察到恰好120個熒光標記分子的概率極低。在實際數據分析時,通常會用泊松分布來擬合整個分子計數的數據集,以獲得總體表達水平、變異性以及不同表達水平下的細胞比例等統計信息。
-
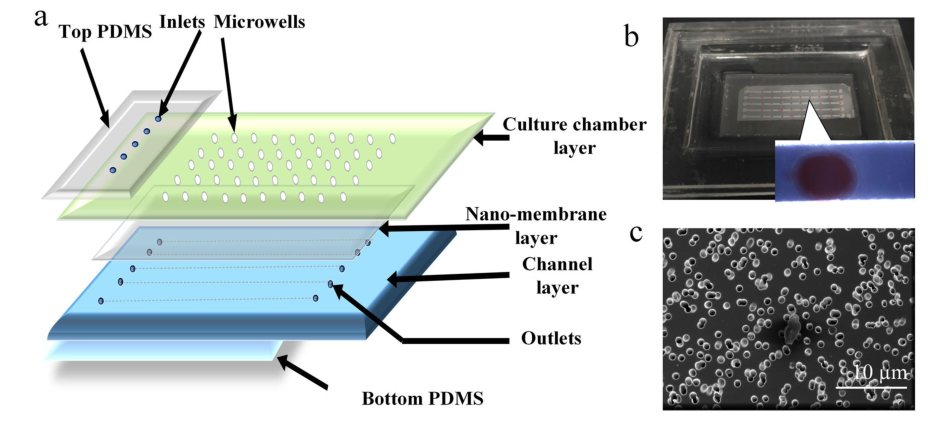
微流控芯片
+關注
關注
13文章
293瀏覽量
19137 -
光信號
+關注
關注
0文章
455瀏覽量
28019 -
RNA
+關注
關注
0文章
46瀏覽量
9848
原文標題:泊松分布在微流控芯片分子免疫檢測中的應用
文章出處:【微信號:gh_38186cae1d9a,微信公眾號:秦嶺農民】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
基于免疫微傳感器的微流體系統
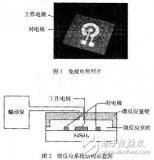
基于免疫微傳感器的微流體系統
POCT中的“顛覆性技術”——微流控芯片應用實例分享
機器學習:泊松分布與指數分布
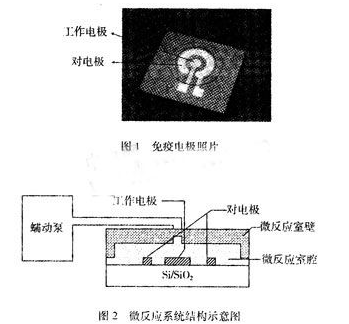
基于MEMS工藝的電極型免疫微傳感器檢測系統設計
基于泊松簇過程的毫米波異構網絡模型







 泊松分布在微流控芯片分子免疫檢測中的應用有哪些
泊松分布在微流控芯片分子免疫檢測中的應用有哪些











評論