安全多方計算
在討論安全多方計算(下文使用 MPC) 之前,我們先討論安全多方計算的設定,在MPC 的所有參與者中,某些參與者可能會被一個敵手 (攻擊者) 控制,在敵手控制下的參與者被稱為被腐化方,它在協議執行過程中會遵循敵手的指令對協議進行攻擊。一個安全的協議應經得起任何敵手的攻擊。為了正式描述和證明一個協議是“安全”的,我們需要對MPC的安全性進行精準定義。
1.安全性
安全多方計算的安全性規范是通過一種理想世界/現實世界的范式 (Ideal/Real Paradigm)來定義的。在理想世界中,存在一個可信的第三方 (Trusted Third Party,TTP),每個參與方將各自的秘密數據通過安全信道提供給可信第三方,由第三方在聯合的數據上進行函數的計算,在完成計算后,可信第三方把輸出發給各個參與方。由于在計算過程中,每個參與者唯一可執行的動作是將秘密數據發送給可信第三方,因此,攻擊者唯一可執行的是選擇被腐化參與者的輸入,且攻擊者除能獲得計算結果以外,不能得到其他任何信息。
與理想世界相對應的是現實世界,現實世界中不存在可信第三方,參與者在沒有任何外部節點幫助下參與協議執行,且部分參與者可能被攻擊者“腐化”或存在合謀。因此,現實世界中的一個安全協議,需要經受它在現實世界的任竟敵手的攻擊,當在理想世界中存在同樣敵手攻擊時,敵手與誠實參與者在理想世界執行中的輸入/輸出數據的聯合分布與現實世界執行中的輸入/輸出數據的聯合分布在計算上不可區分,即在理想世界中模擬了現實世界的協議執行。
理想世界/現實世界范式是為了確保滿足“安全性”所隱含的多個屬性。
1) 隱私:任何一方都不應該獲取超過它規定的輸出,特別是不應該從輸出信息中獲取其他合作方的輸入信息。攻擊者在理想世界中獲取不到任何除被腐化方輸出以外的其他信息,那么在現實世界中也同樣如此。
2) 正確性:保證每一方收到的輸出都是正確的。誠實參與者在現實世界所得到的輸出與理想世界從可信第三方得到的輸出是相同的。
3) 輸入獨立性:被腐化的參與者所選擇的輸入必須與誠實參與者輸人無關。在理想世界的協議執行中,被腐化參與者在發送輸入給可信第三方時,無法獲取誠實參與者的任何輸入信息。
4) 保證輸出:被腐化的參與者不應當具備阻止誠實參與者獲取輸出的能力。
5)公平性:當且僅當誠實參與者獲取輸出時,被腐化的參與者才能獲取輸出,即不存在被腐化參與者獲取了輸出而誠實參與者未獲取輸出的情況。在理想世界中,可信第三方總是將輸出返回給所有參與者。因此可以保證輸出和公平性。這也意味著在現實世界中,誠實參與者得到與理想世界同樣的輸出。
2.參與者
我們需要對 MPC 的參與者進行定義:MPC 的參與者是指參與協議的各方,每個參與者可被抽象為具有概率多項式時間算法 (Probabilistic Polynomial Time Algorithm,PPT Algorithm)的交互圖靈機。根據協議執行過程中的敵手對參與者的控制能力/權利,可將被腐化參與者分為三種敵手類型。
1) 半誠實敵手:這類參與者會按照協議的要求執行各個步驟。然而,半誠實敵手會設法獲取所有協議執行過程中的信息 (包括執行腳本和所有接收到的消息),并試圖推導額外的隱私信息。
2) 惡意敵手:這類參與者在執行協議過程中,完全按照攻擊者的指令執行協議的各個步驟,不僅會將所有的輸入、輸出,以及中間結果泄露給攻擊者,還會根據攻擊者的意圖改變輸入信息、偽造中間及輸出信息,甚至終止協議。
3) 秘密敵手:這種類型的敵手可能對協議進行惡意攻擊,一旦它發起攻擊,有一定的概率會被檢測到。如果沒有被檢測到,那么它就可能完成了一次成功的攻擊 (發起攻擊是為了獲取額外的信息)。
因此,根據安全多方計算協議中的不同參與者在現實世界的攻擊行為,可將協議的安全模型進行如下劃分。
1)半誠實模型 (The Semi-Honest Model):在協議執行時,參與者按照協議規定的流程執行,但是可能會被惡意攻擊者監聽并獲取到在協議執行過程中自己的輸入、輸出,以及在協議運行過程中獲得的信息。
2)惡意模型 (The Malicious Model):在協議執行時,攻擊者可以利用在其控制下的參與者,通過不合法的輸入或者惡意篡改輸入等方法來分析誠實參與者的隱私信息,還可以通過提前終止和拒絕參與等方式導致協議終止。
另外,根據敵手何時及如何控制參與方,可以將敵手的腐化策略分為下列三種模型。
1)靜態腐化模型 (Static Corruption Model):在該模型中,在協議開始之前,由敵手固定控制一組合作方。誠實的合作方始終是誠實的,腐化的合作方始終是腐化的。
2)自適應腐化模型 (Adaptive Corruption Model):敵手能夠自主決定什么時間對哪個參與者進行腐化,需要注意的是,一旦一個參與者被腐化,它將始終保持腐化狀態。
3)主動安全模型(Proactive Security Model):誠實參與者可能在某一段時間被腐化,被腐化參與者也可能在某一段時間變為誠實參與者。主動安全模型是從一個可能存在入侵網絡、服務或設備的外部敵手的角度來講的,當網絡被修復時,敵手失去了對機器的控制,被腐化的參與者變為誠實參與者。
在現實世界中,MPC 協議不是孤立運行的,通常是對協議進行模塊序列化組合或與其他協議并行 (運行) 組合得到一個更大的協議來運行。
有研究證明,如果一個 MPC 協議在一個更大的協議中按序列運行,則它仍然遵守現實/理想世界范式,即存在一個可信第三方執行該協議并輸出對應結果。這個理論被稱為“模塊化組合”,它允許使用安全子協議以模塊化的方式構造更大的協議,以及分析一個使用MPC 進行某些計算的更大的系統。
對于協議并行運行的情況,當有其他協議與當前協議并行運行時,若該協議不需要其他并行協議發送任何消息,則可將該假設稱為協議的獨立設定,它也是 MPC 安全性的基本安全定義。在獨立設定下,一個并行運行的協議與可信第三方執行的行為一樣。
最后,在一些其他場景中,MPC 協議可能與該協議的其他實例,或其他 MPC 協議,抑或其他不安全協議并行運行,協議實例可能需要與其他實例進行交互,此時該協議的運行可能是不安全的。協議在理想世界中不包含與其他協議 (功能函數) 的交互,而在現實世界中需要與另一個功能函數進行交瓦,與理想世界的模擬存在不同的執行條件 (可將此時的現實世界稱為混合世界)。在這種情況下,主流的方式是采用“通用組合”(Universal Composability) 進行安全定義,在此定義下,任何被證明是安全的協議都被保證按照理想的行為執行,而不論它與其他任何協議是否并行執行。
MPC 的安全定義具有重要作用,具體地講,如果一個 MPC 協議在現實世界是安全的,那么對于一個使用 MPC 協議的從業人員,他可以僅考慮該 MPC 協議在理想世界中的執行情況,即對于非密碼學的 MPC 協議的使用者,可以不考慮 MPC 協議如何運行,或者該協議是否安全,因為理想模型對 MPC 的功能提供了更清晰和更簡單的抽象。
盡管理想模型提供了簡單的抽象,但有些情況下容易產生如下問題。
在現實世界中,敵手可能輸入任何值,且 MPC 協議沒有通用的解決方案來防止這種情況。例如,對于“百萬富翁”問題,敵手可以任意輸入被腐化參與者的財富量 (比如直接輸入最大值),那么敵手腐化方永遠是“勝利”的一方。如果一個 MPC 協議的應用依賴于參與者的正確輸入,那么需要通過其他技術增強/驗證參與者輸入的正確性。
MPC 協議僅保證計算過程安全,而無法保證輸出安全。MPC 協議的輸出結果在各參與者揭秘之后,給出的輸出結果可能會透露其他參與者的輸入信息。例如,需要計算兩個參與者薪資的平均數,MPC 協議可以保證除輸出平均薪資以外不會輸出任何其他信息。但是,其中一個參與者完全可以根據自己的薪資和平均薪資,計算出另一個參與者的薪資。因此,使用 MPC 并不意味著所有信息都能受到保護。
在實踐過程中,考慮到 MPC 的計算和通信開銷問題,通常會以半誠實模型為主要安全設定。因此,本書中討論的 MPC 協議也主要以半誠實模型的協議為主,雖然部分 MPC 協議可以同時支持半誠實和惡意安全性,但本文仍主要關注 MPC 協議的半誠實設定。
密碼學
密碼學是隱私計算技術的重要基礎,在隱私計算的各個技術路線中經常被使用。密碼學理論體系非常龐大且復雜,感興趣的讀者可參考《現代密碼學及其應用》等圖書擴展學習,本文僅對密碼學的基礎知識和隱私計算中常用密碼學原語進行簡單介紹。
在MPC 協議中,經常會使用兩種數據加密方式:對稱加密和非對稱 (公鑰) 加密。
對稱加密是應用較早的加密算法,其技術成熟。因為加密和解密使用同一個密鑰,所以它被稱為對稱加密。常見的對稱加密算法有 DES、AES、IDEA 等。
非對稱加密也叫作公鑰加密。與對稱加密不同的是,非對稱加密算法需要兩個密鑰:公 (public key) 和私鑰 (private key),且二者成對出現。私鑰被自己保存,不能對外泄露。公鑰指的是公共的密鑰,任何人都可以獲得該密鑰。通常使用公鑰對數據進行加密,使用私鑰進行解密。非對稱加密還有另一種用法,即數字簽名,使用私鑰對數據進行簽名,使用公鑰進行驗簽。數字簽名可以讓公鑰持有者驗證私鑰持有者的身份并且防止私鑰持有者發布的內容被篡改。常見的非對稱加密算法有 RSA、EIGamal、D-H、ECC 等。
1.橢圓曲線加密
橢圓曲線加密是一種公鑰加密技術,它常常與其他公鑰加密算法結合以得到對應橢圓曲線版本加密算法。通常認為,橢圓曲線可以使用更短的密鑰而達到更高的安全性。
橢圓曲線加密是將實數域上的橢圓曲線加法群限制在素數域內,基于離散對數困難問題構造的加密算法。實數域上的一個橢圓曲線通常可通過一個二元三次方程定義,以常用的Weierstrass橢圓曲線方程為例:
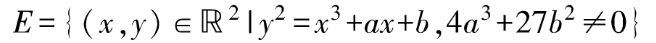
其中,a、b 為可配置參數。該橢圓曲線方程對應的所有解 (二維平面在該方程對應曲線上所有的點)再加上一個無窮遠處的點0 (群的單位元,0 點)構成該橢圓曲線的元素集合。在這些點的集合上,再定義對應的滿足封閉、交換、結合性質的加法計算和逆元計算,即可構成橢圓曲線加法群。通過修改橢圓曲線不同的參數a、b,即可得到不同的圓曲線群。
對于橢圓曲線上的兩個點 P、Q,首先定義經過兩個點的直線以及與橢圓曲線的交點 R,P與Q在橢圓曲線上的加法結果為 R 關于x軸的對稱點。這個加法操作定義包含了多種情況,如圖2所示。
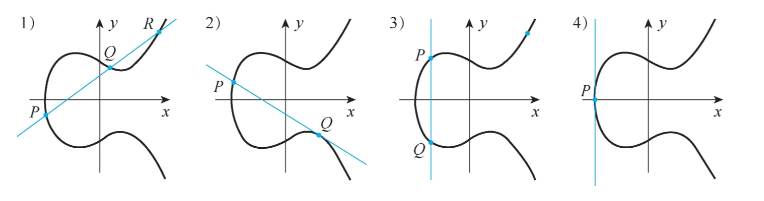
圖2. 橢圓曲線四種不同點加法情況
P、Q 不是切點且不互為逆元,則有第三個交點 R,此時 P+Q=-R。
P或Q為切點 (假設為 0),此時 P與0連接后的線稱為切線,則定義 R=O,此時P+Q+Q=0。即加法結果為 P+O=-Q。
若 P與Q的連線垂直于x軸,此時連線與橢圓曲線沒有交點,則認為交點位于無窮遠處,即 P+Q=0。
若 P=Q,則此時認為連線為橢圓曲線在 P 點的切線;若該切線與橢圓曲線有交點R,則結果為-R,否則認為交點為無窮遠處點。
橢圓曲線的加法具體到實現上,則是先計算 P與Q連線的斜率
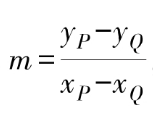
然后根據韋達定理計算交點 R的坐標:
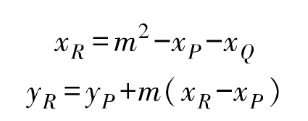
若P和Q為同一點,其斜率計算修改為
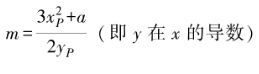
然后按照上式計算 R的坐標。
橢圓曲線的標量乘法 (或稱多倍點運算) 可以通過點的多次相加實現,如nP表示對n個P點進行加法:
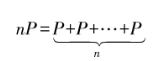
由于橢圓曲線加法群滿足交換律和結合律,因此可通過 Double-and-Add 算法進行優化。
在將橢圓曲線加法群應用到加密時,通常需要將橢圓曲線的元素限制在一個素數域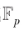 內,于是可基于其標量乘法構造離散對數難題。素數域的橢圓曲線定義如下:
內,于是可基于其標量乘法構造離散對數難題。素數域的橢圓曲線定義如下:
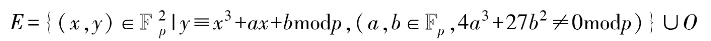 a=-1,b=3 的一個素數域橢圓曲線點分布如圖 3 所示。
a=-1,b=3 的一個素數域橢圓曲線點分布如圖 3 所示。
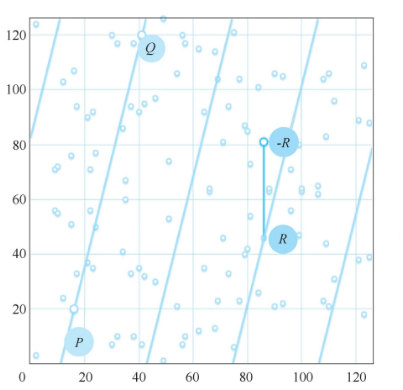
圖3
對于定義在素數域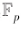 上的橢圓曲線的點,其坐標的加法和標量乘法與實數域計算規則一樣,但所有的計算均需要在素數域E進行。如圖1-3 所示的 P點 (16,20)與0點(41.120)的交點為 R (86,46)在素數域F定義下的 PO 直線上[素數域下。上的直線定義為所有滿足 ax+by+c三0(modp)的點T,其加法結果-R(86,81)。
上的橢圓曲線的點,其坐標的加法和標量乘法與實數域計算規則一樣,但所有的計算均需要在素數域E進行。如圖1-3 所示的 P點 (16,20)與0點(41.120)的交點為 R (86,46)在素數域F定義下的 PO 直線上[素數域下。上的直線定義為所有滿足 ax+by+c三0(modp)的點T,其加法結果-R(86,81)。
同樣,根據加法計算規則,可得到素數域的標量乘法,當標量 n 很大時,計算 Q=nP后,將Q點作為公鑰,n 作為私鑰,已知P、Q計算n 就構造了素數域圓曲線的離散對數難題。顯然,若 n 定義在整數域,則P 的標量乘法所遍歷得到的點集構成了該橢圓曲線的循環子群,為保證安全性,需要使 P的標量乘法覆蓋的點足夠多(子群的階足夠大),因此需要找到一個元素階較高的基點。
尋找基點的一個簡單方法是,首先根據橢圓曲線的階N確定子群的階n(需要為素數),計算余因子h=N/n,然后在橢圓曲線中隨機選擇點 P,計算 G=hP,若 G=0,則重新選擇點,否則點 G 即為基點。
有多個主流的被認為安全的橢圓曲線及參數可供選擇,如比特幣簽名中的橢圓曲線secp256k1、curve25519等;在開源框架FATE 中,實現了扭曲愛德華曲線Edwards25519。
密文計算
若經過加密的密文可進行直接計算,則可將對應的加密技術稱為同態加密。“同態”的概念來自于抽象代數中的同態映射,它是指兩個代數系統(群/環/域)之間能保持運算的一類映射,即對于代數系統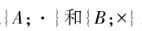 ,若經過某個映射
,若經過某個映射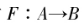 后,對
后,對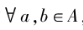 ,有F(A·B)= F(A)XF(B),則可稱F為A到B的同態映射。
,有F(A·B)= F(A)XF(B),則可稱F為A到B的同態映射。
若一個明文經過某種加密算法,其密文進行與明文“對應的”密文運算后,解密得到與明文運算相同的結果,則可認為該加密算法具有同態性質,即可對明文進行同態加密。同態加密根據支持的計算類型和支持程度,可分為三種類型:半同態加密 (Partially Homomorphic Encryption,PHE)、近似全同態加密 (SomeWhat Homomorphic Encryption,SWHE) 和全同態加密 ( Fully Homomorphic Encryption,FHE)。
(1) 半同態加密
半同態加密是指只支持加法或乘法運算的加密算法,可分別稱為加法同態和乘法同態。常見的半同態加密算法包括RSA、EIGamal、ECC-EIGamal、Paillier,其中 RSA 和EIGamal具有乘法同態性質,ECC-EIGamal和Paillier具有加法同態性質。Paillier 是常用的一個半同態加密算法。它依賴于復合剩余類的困難問題構造,經過多年研究,已被證實非常可靠,且在多個開源隱私計算框架中經常被使用。下面將對 Paillier 原理做簡要介紹。
一個 PHE 通常包含以下幾個功能。
KeyGen():密鑰生成,用于產生加密數據的公鑰 pk 和私鑰 sk,以及一些公共參數( public parameter)。
Encrypt():加密算法,使用pk 對用戶數據 m 進行加密,得到密文 (ciphertext) c。
Decrypt():解密算法,使用 sk 對密文c解密,得到數據原文 (plaintext) m。
Add():密文同態加法,輸入兩個密文 c1、c2,進行同態加運算。
ScalaMul():密文同態標量乘法,輸入 c 和一個標量 s,計算c與標量乘的結果。
對于 Paillier 加密,其各個算法功能的實現如下。
KeyGen()。隨機生成兩個獨立的大素數p 和q,滿足gcd(pg,(p-1)(q-1))=1,且p、q長度相等。計算n=pq,A=lcm(p-1,q-1),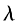 =
=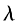 (n)為n 的卡邁克爾函數,Icm 為最小公倍數。隨機選擇
(n)為n 的卡邁克爾函數,Icm 為最小公倍數。隨機選擇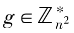 ,不妨設 g=n+1,并定義L函數
,不妨設 g=n+1,并定義L函數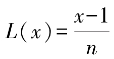 ,
,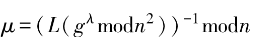 。返回公鑰 (n,g)和私鑰 (
。返回公鑰 (n,g)和私鑰 (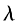 ,
,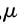 )。
)。
2)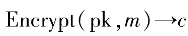 。輸入明文消息m,隨機選擇
。輸入明文消息m,隨機選擇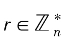 ,計算密文
,計算密文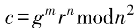 。
。
3)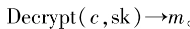 。輸入密文消息c,計算
。輸入密文消息c,計算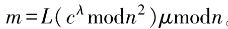 。
。
解密的正確性可根據卡邁克爾函數性質,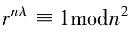 及二項式定理(1+x)”=1+
及二項式定理(1+x)”=1+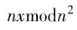 推導驗證。
推導驗證。
由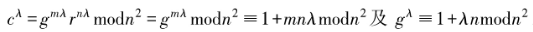 可得
可得
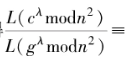
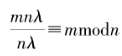 。
。
4)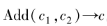 。輸入密文
。輸入密文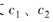 ,其密文加法被定義為
,其密文加法被定義為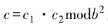 正確性可驗證:
正確性可驗證: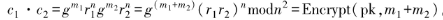 。
。
5)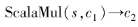 。輸入密文c 和標量s,其標量乘法被定義為
。輸入密文c 和標量s,其標量乘法被定義為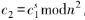
正確性可驗證: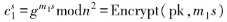 。
。
(2) 近似全同態加密
近似全同態加密 (有限級數同態加密)是同時支持密文加法和密文乘法的加密算法,但它往往僅能支持有限級數的密文乘法。近似全同態加密是大部分全同態加密的基礎。全同態加密算法往往會在近似全同態加密方案上加人一個自舉(Bootstraping)或漸進式的模數切換 (Modulus Switching)。全同態加密算法起源于 2009年 Gentry 提出的方案,通過對近似全同態加密算法加入自舉操作,控制運算過程中噪聲的增長。自舉方法是指通過將解密過程本身轉化為同態運算電路,并生成新的公私鑰對,對原私鑰和含有噪聲的原密文進行加密,然后用原私鑰的密文對原密文的密文進行解密的同態運算,其可得到不含噪聲的新密文。
(3) 全同態加密
Gentrv于2009年提出一種基于電路模型的全同態加密算法,它僅支持對每個比特進行加法和乘法同態運算(布爾運算)。目前主流的同態加密方案基于格上 LWE Learning With Errors)/Ring-LWE (RLWE) 問題構造,LWE/RLWE 都可以規約到基于格上的困難問題【如最短線性無關向量 (SIVP) 問題】,然而LWE 問題中涉及矩陣與向量的乘法,計算較復雜,而基于 RLWE 的問題僅涉及環上多項式的運算,具有更小的計算開銷。因此,雖然主流的同態加密算法 (如BGV、BFV 等)都可同時基于LWE/RLWE 構造,但在實現上會以RLWE 為主。另外,Cheon 等人在 2017 年提出了一種浮點數的全同態加密方案--CKKS,該方案支持針對實數或復數的浮點數加法和乘法同態運算,得到的計算結果為近似值,它通常適用于機器學習模型訓練等不需要精確結果的場景。
3.偽隨機函數
隱私計算中另一個被廣泛使用的密碼學原語為偽隨機函數 (Pseudo Random Function)。一個偽隨機函數是一個形如 y= F(k,x)的確定性函數,其中是密鑰空間K 的一個密鑰,x 是輸人空間X的一個元素,y 是輸出空間Y上的一個元素。其安全性要求:給定一個隨機密鑰k,函數 F(k,·)應該看上去像一個定義在X到Y的隨機函數。Oded 等人證明了通過偽隨機數生成器可構造偽隨機函數。
三、機器學習
從隱私計算根據其保護的計算過程來看,有一大類是隱私保護的機器學習。機器學習根據其學習方式通常可分為三種類型:監督學習、半監督學習和無監督學習。
監督學習是在給定帶標簽/標記訓練數據下的學習方式,其目標是在給定的訓練數據集中學習到一個模型(函數),當新數據出現時,可根據這個函數給出預測結果。常見的監穆學習算法包括樸素貝葉斯、邏輯回歸、線性回歸、決策樹、集成樹、支持向量機、(深度)神經網絡等。然而,很多實際問題中,因為對數據進行標記的代價有時很高,所以通常只能拿到少量標簽數據和大量的無標簽數據。半監督學習是在給定較少帶標簽訓練數據和大量無標簽數據下的學習方式,它使用無標簽數據來獲得數據結構更多的信息,其目標是要得到比單獨使用帶標簽數據訓練的監督學習技術更好的結果。常見的半監督學習策略包括 selftraining、PU Learning、Co-training 等。無監督學習中的常見任務有聚類、表示學習和密度估計。這些任務都是希望在無明確提供的標簽的情況下了解數據的內在結構。常見的無監督學習算法包括 k-means 聚類、主成分分析和自動編碼器等。由于沒有提供標簽,因此在多數無監督學習算法中沒有用于比較模型性能的具體方法。
在實際應用中,監督學習應用范圍比較廣,因此本文以監督學習為主對一些基本概念進行介紹。
1.損失函數
監督學習通常給出帶標簽訓練數據 (x,y),x作為輸入數據,通常由一個向量表示,向量的每個元素稱為特征;y為模型需要學習的輸出數據,通常也稱為標簽。訓練數據一般由多條 (x,y) 數據組成,每條 (x,y) 數據被稱為一個樣本,所有樣本的輸入組成輸入空間/特征空間X,所有輸出標簽組成輸出空間 Y。根據輸出空間的分布,可將監督學習劃分為分類模型和回歸模型,分類模型通常根據輸出標簽 y的基數分為二分類模型和多分類模型.
因此,監督學習的目標是通過一個學習算法,在訓練集 X×Y 上找到一個模型f(x,w)使模型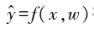 得到的預測值
得到的預測值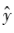 與真實輸出值一致。然而,模型的預測值
與真實輸出值一致。然而,模型的預測值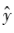 可能與y一致或不一致。因此,需要使用一個損失函數來量化模型預測值
可能與y一致或不一致。因此,需要使用一個損失函數來量化模型預測值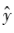 與真實值y的差異(一般稱
與真實值y的差異(一般稱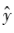 -y為殘差)。損失函數 L(y,f(x,w))是一個非負實值函數,需要根據監督學習的任務類型進行不同定義。常用的損失函數包括 0-1 損失函數、平方損失函數、對數損失函數、交叉損失函數、合頁損失函數等。然而,前面的損失函數僅僅是定義在訓練數據集上的期望損失,通常被稱為經驗損失或經驗風險,只有當樣本數量趨于無窮大時,才可認為其損失是期望的損失 (通常也被稱為期望風險)。當模型參數復雜而訓練數據較少時,可能會存在模型在訓練數據上預測正確性很高,而在訓練集外的未知數據集上預測正確性較低的現象,這種現象被稱為“過擬合”。為了防止“過擬合”現象,通常會在經驗損失基礎上加入參數正則化項(正則化損失),限制模型參數對的復雜度,這個新的損失函數可稱為結構化損失函數(或結構風險函數)。
-y為殘差)。損失函數 L(y,f(x,w))是一個非負實值函數,需要根據監督學習的任務類型進行不同定義。常用的損失函數包括 0-1 損失函數、平方損失函數、對數損失函數、交叉損失函數、合頁損失函數等。然而,前面的損失函數僅僅是定義在訓練數據集上的期望損失,通常被稱為經驗損失或經驗風險,只有當樣本數量趨于無窮大時,才可認為其損失是期望的損失 (通常也被稱為期望風險)。當模型參數復雜而訓練數據較少時,可能會存在模型在訓練數據上預測正確性很高,而在訓練集外的未知數據集上預測正確性較低的現象,這種現象被稱為“過擬合”。為了防止“過擬合”現象,通常會在經驗損失基礎上加入參數正則化項(正則化損失),限制模型參數對的復雜度,這個新的損失函數可稱為結構化損失函數(或結構風險函數)。
2.梯度下降
在定義了損失函數之后,便可以通過優化方法尋找模型參數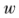 ,使損失值不斷下降,損失值越低,則可認為模型預測值
,使損失值不斷下降,損失值越低,則可認為模型預測值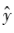 與真實輸出值y之間的差異越小。一種常見的參數優化方法是梯度下降法,對于每次訓練迭代,先計算損失函數對參數的梯度 (一階連續偏導數),用梯度的反方向 (梯度的負數) 乘以一定步長 lr(學習速率),對參數進行更新:
與真實輸出值y之間的差異越小。一種常見的參數優化方法是梯度下降法,對于每次訓練迭代,先計算損失函數對參數的梯度 (一階連續偏導數),用梯度的反方向 (梯度的負數) 乘以一定步長 lr(學習速率),對參數進行更新:
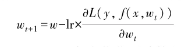
步長lr 可以固定為一個比率,也可以通過各類優化器計算得到一個自適應的比率。梯度下降按照訓練樣本的選取策略可分為隨機梯度下降 (每次隨機選取一個樣本)、批量梯度下降(每次使用所有樣本)和小批量 (mini batch) 梯度下降(每次按順序選取一批樣本)。
在聯邦學習中,有標簽一方可直接計算梯度,在無標簽一方,梯度必須在密態方式下計算,可通過有標簽一方對殘差進行同態加密并發送給無標簽一方計算,也可以通過 MPC 方式聯合計算。
3.深度學習
深度學習是近年來非常流行的一種機器學習方法。與傳統機器學習相比,深度學習主要采用深度神經網絡作為特定模型結構,通過對網絡結構的層結構、層連接方式、連接權重采樣、單元結構、激活函數、學習策略、正則化等多種方式優化,實現遠超傳統機器學習的模型性能。多種經典的深度學習技術被廣泛采用,包括卷積神經網絡 (Convolutional Neural Networks,CNN)、圖卷積神經網絡 (GCN)、Dropout、Poling、長短期記憶網絡 (LongShort-Term Memory,LSTM)、RNN、GRU、殘差網絡、DQN、DDQN、Batch Normalization.Layer Normalization、 Attention 、Transformer 等。
由于深度學習模型復雜、參數量大,而隱私計算中很多計算涉及密文計算,因此,在實際應用中,通常會使用網絡層級更少、結構更為簡單的神經網絡,如 CNN、Dropout、Pooling、Batch Normalization、Layer Normalization 等。隱私計算中有多種實現方案,如在聯邦學習中,通常首先會在參與方本地進行神經網絡的前向計算,然后在協調節點上進行梯度計算,最后在各本地進行網絡的反向傳播。MPC 實現的深度神經網絡則通常將模型參數和數據進行秘密共享,進行全密態的訓練或預測。基于全同態加密的方案 CKKS 可直接在全密態下(數據加密或模型加密) 進行網絡的訓練和預測,且可以滿足模型和數據的完全分離。
審核編輯:湯梓紅
-
函數
+關注
關注
3文章
4345瀏覽量
62877 -
機器學習
+關注
關注
66文章
8438瀏覽量
132928 -
深度學習
+關注
關注
73文章
5512瀏覽量
121413 -
深度神經網絡
+關注
關注
0文章
61瀏覽量
4547
原文標題:隱私計算迎來千億級風口,一文講清它的技術理論基礎
文章出處:【微信號:釋然IT雜談,微信公眾號:釋然IT雜談】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
存內計算技術工具鏈——量化篇




 安全多方計算技術解析
安全多方計算技術解析










評論