作者:nghuyong
在大模型的研發中,通常會有下面一些需求:
1.計劃訓練一個10B的模型,想知道至少需要多大的數據?
2.收集到了1T的數據,想知道能訓練一個多大的模型?
3.老板準備1個月后開發布會,給的資源是100張A100,應該用多少數據訓多大的模型效果最好?
4.老板對現在10B的模型不滿意,想知道擴大到100B模型的效果能提升到多少?
以上這些問題都可以基于Scaling Law的理論進行回答。本文是閱讀了一系列 Scaling Law的文章后的整理和思考,包括Scaling Law的概念和推導以及反Scaling Law的場景,不當之處,歡迎指正。
核心結論
大模型的Scaling Law是OpenAI在2020年提出的概念[1],具體如下:
對于Decoder-only的模型,計算量(Flops), 模型參數量, 數據大小(token數),三者滿足:。(推導見本文最后)
模型的最終性能主要與計算量,模型參數量和數據大小三者相關,而與模型的具體結構(層數/深度/寬度)基本無關。
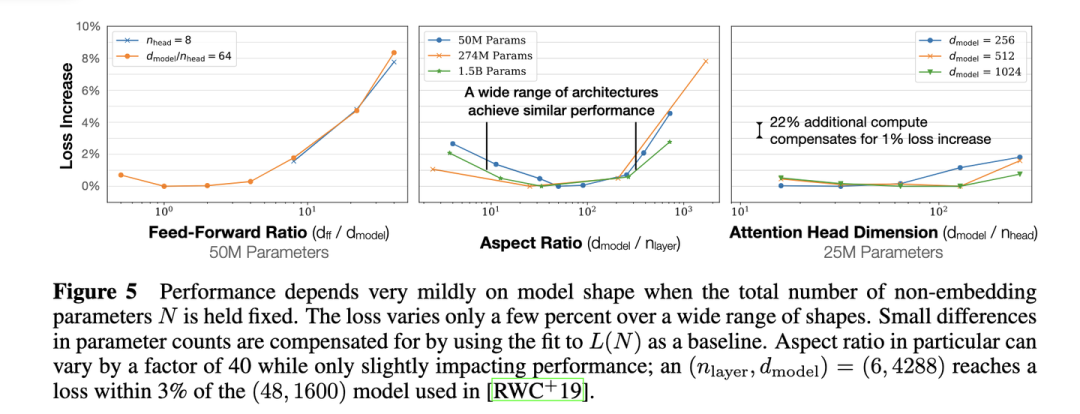
固定模型的總參數量,調整層數/深度/寬度,不同模型的性能差距很小,大部分在2%以內
3.對于計算量,模型參數量和數據大小,當不受其他兩個因素制約時,模型性能與每個因素都呈現冪律關系
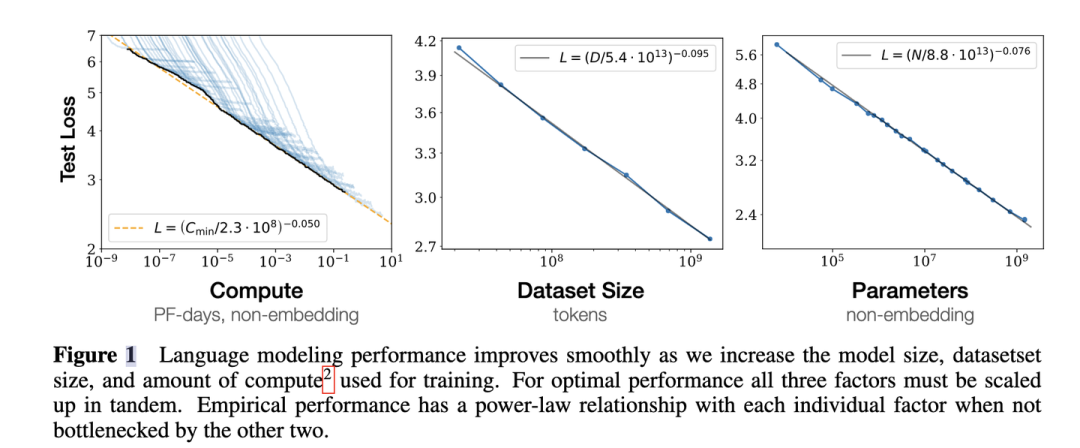
4. 為了提升模型性能,模型參數量和數據大小需要同步放大,但模型和數據分別放大的比例還存在爭議。
5. Scaling Law不僅適用于語言模型,還適用于其他模態以及跨模態的任務[4]:
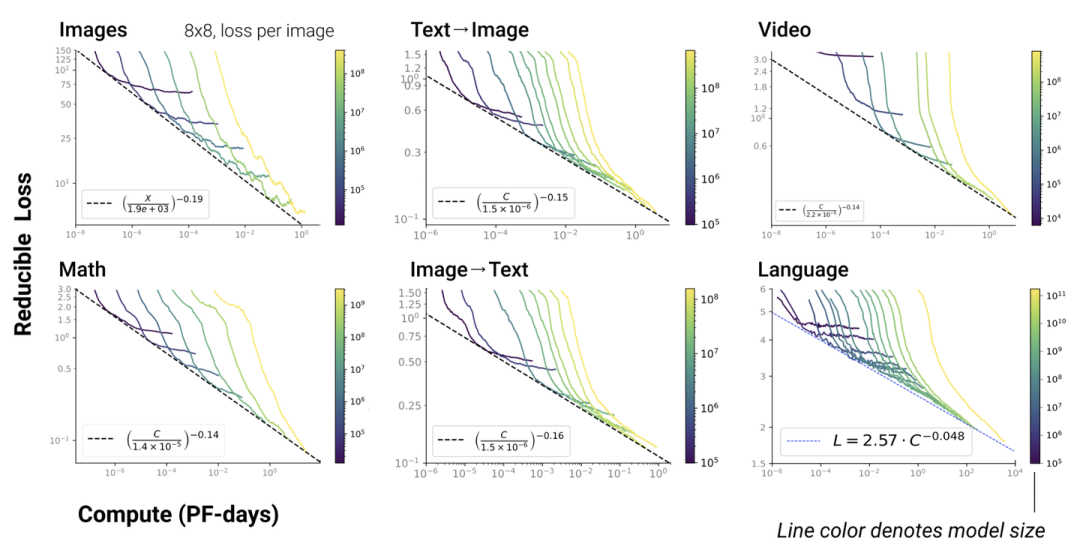
這里橫軸單位為PF-days: 如果每秒鐘可進行次運算,就是1 peta flops,那么一天的運算就是這個算力消耗被稱為1個petaflop/s-day。
核心公式
(?)=?∞+(?0?)?

第一項是指無法通過增加模型規模來減少的損失,可以認為是數據自身的熵(例如數據中的噪音)
第二項是指能通過增加計算量來減少的損失,可以認為是模型擬合的分布與實際分布之間的差。根據公式,增大(例如計算量),模型整體loss下降,模型性能提升;伴隨趨向于無窮大,模型能擬合數據的真實分布,讓第二項逼近0,整體趨向于
大模型中的scaling law
下圖是GPT4報告[5]中的Scaling Law曲線,計算量和模型性能滿足冪律關系
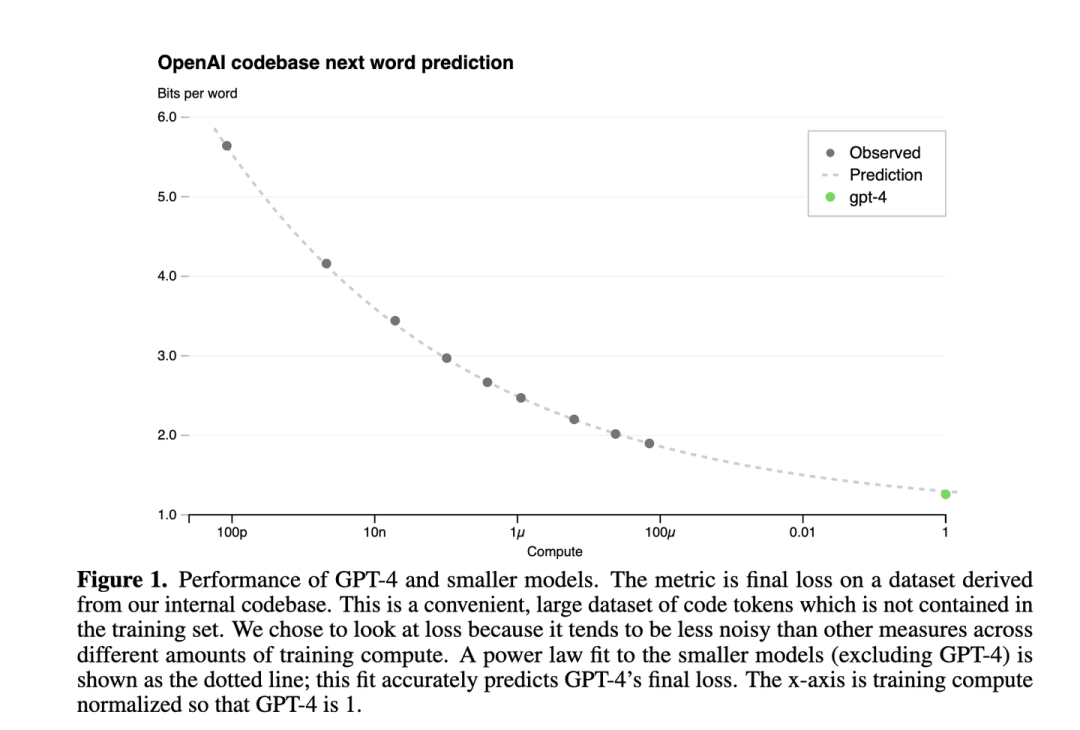
橫軸是歸一化之后的計算量,假設GPT4的計算量為1。基于10,000倍小的計算規模,就能預測最終GPT4的性能。
縱軸是"Bits for words", 這也是交叉熵的一個單位。在計算交叉熵時,如果使用以 2 為底的對數,交叉熵的單位就是 "bits per word",與信息論中的比特(bit)概念相符。所以這個值越低,說明模型的性能越好。
Baichuan2
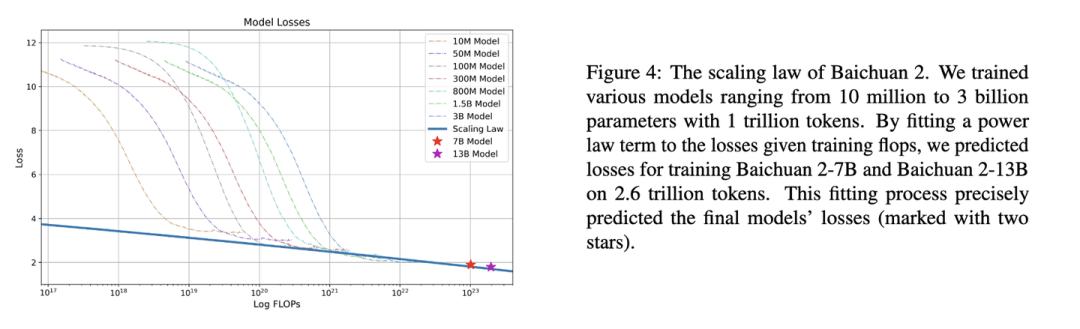
下圖是Baichuan2[6]技術報告中的Scaling Law曲線。基于10M到3B的模型在1T數據上訓練的性能,可預測出最后7B模型和13B模型在2.6T數據上的性能
MindLLM
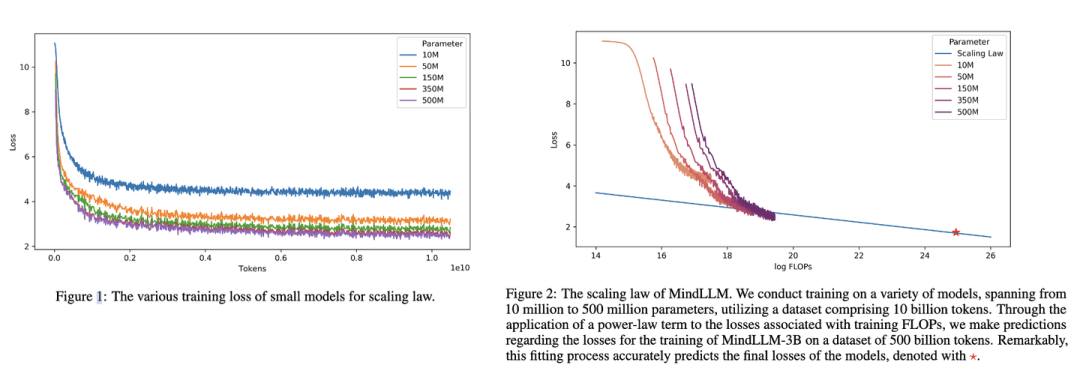
下圖是MindLLM[7]技術報告中的Scaling Law曲線。基于10M到500M的模型在10B數據上訓練的性能,預測出最后3B模型在500B數據上的性能。
Scaling Law實操: 計算效率最優
根據冪律定律,模型的參數固定,無限堆數據并不能無限提升模型的性能,模型最終性能會慢慢趨向一個固定的值
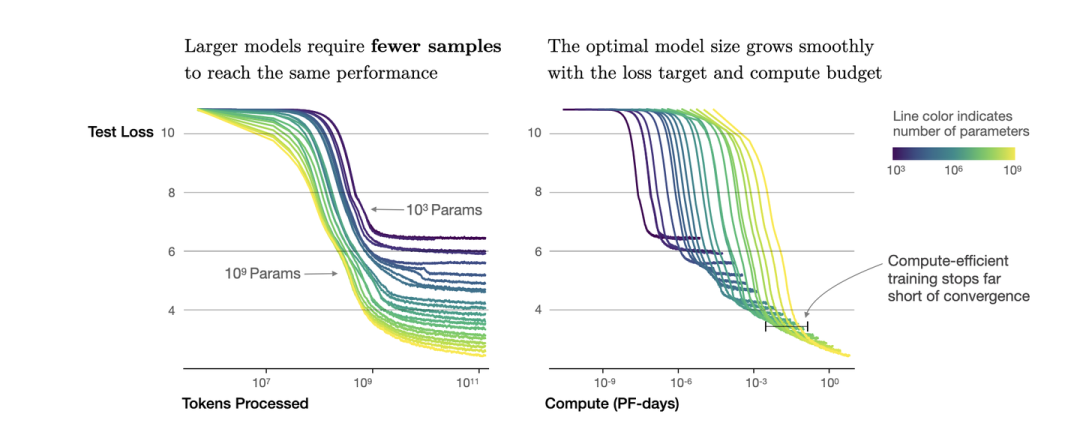
如圖所示,如果模型的參數量為(圖中紫色的線),在數量達到,模型基本收斂。所以在數據量達到后,繼續增加數據產生的計算量,沒有同樣計算量下提升模型參數量帶來的收益大(計算效率更優)。根據,可以進一步轉換成模型參數與計算量的關系,即: 模型參數為,在計算量為Flops,即PF-days時基本收斂。也就是右圖中紫色線的拐點。
按照上面的思路,下面進行Scaling Law的實操。
首先準備充足的數據(例如1T),設計不同模型參數量的小模型(例如0.001B - 1B),獨立訓練每個模型,每個模型都訓練到基本收斂(假設數據量充足)。根據訓練中不同模型的參數和數據量的組合,收集計算量與模型性能的關系。然后可以進一步獲得計算效率最優時,即同樣計算量下性能最好的模型規模和數據大小的組合,模型大小與計算量的關系,以及數據大小與計算量的關系。
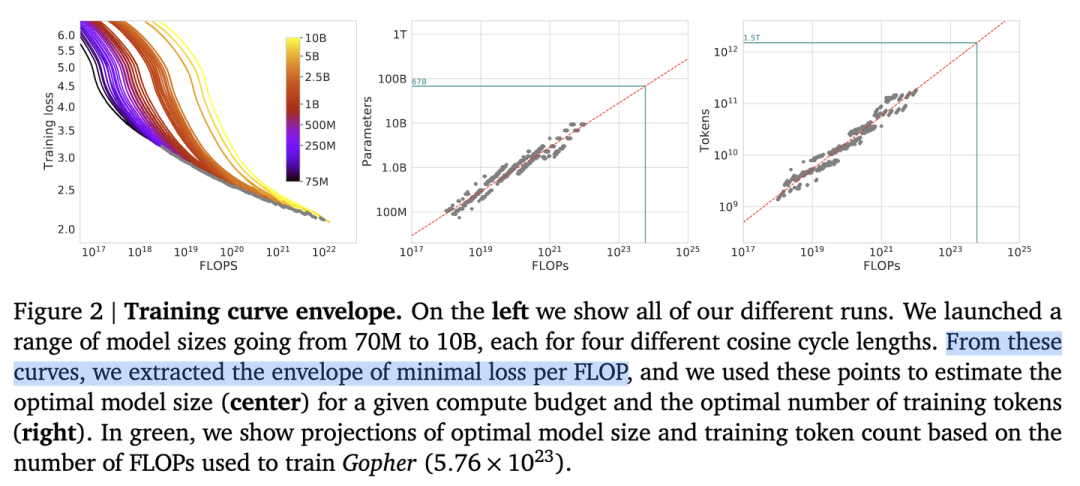
如圖所示,根據左圖可以看到計算量與模型性能呈現冪律關系(可以認為數據和模型都不受限制),根據中圖和右圖,可以發現,,即計算效率最優時,模型的參數與計算量的冪次成線性關系,數據量的大小也與計算量的冪次成線性關系。
根據,可以推算出,但是,分別是多少存在分歧。
OpenAI[1]認為模型規模更重要,即,而DeepMind在Chinchilla工作[2]和Google在PaLM工作[3]中都驗證了,即模型和數據同等重要。
所以假定計算量整體放大10倍,OpenAI認為模型參數更重要,模型應放大100.73(5.32)倍,數據放大100.27(1.86)倍;后來DeepMind和Google認為模型參數量與數據同等重要,兩者都應該分別放大100.5(3.16)倍。
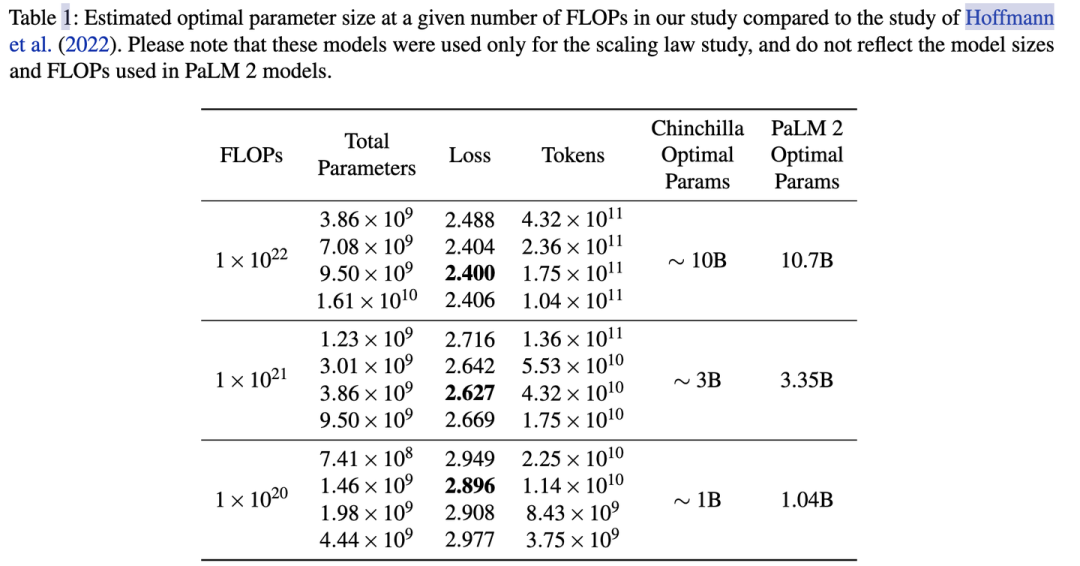
例如在PaLM的實驗中,計算量從 放大10倍到, 模型參數也提升了3.2倍,3.35B->10.7B。具體最好在自己的數據上做實驗來獲得你場景下的和
LLaMA: 反Scaling Law的大模型
假設遵循計算效率最優來研發LLM,那么根據Scaling Law,給定模型大小,可以推算出最優的計算量,進一步根據最優計算量就能推算出需要的token數量,然后訓練就行。
但是計算效率最優這個觀點是針對訓練階段而言的,并不是推理階段,實際應用中推理階段效率更實用。
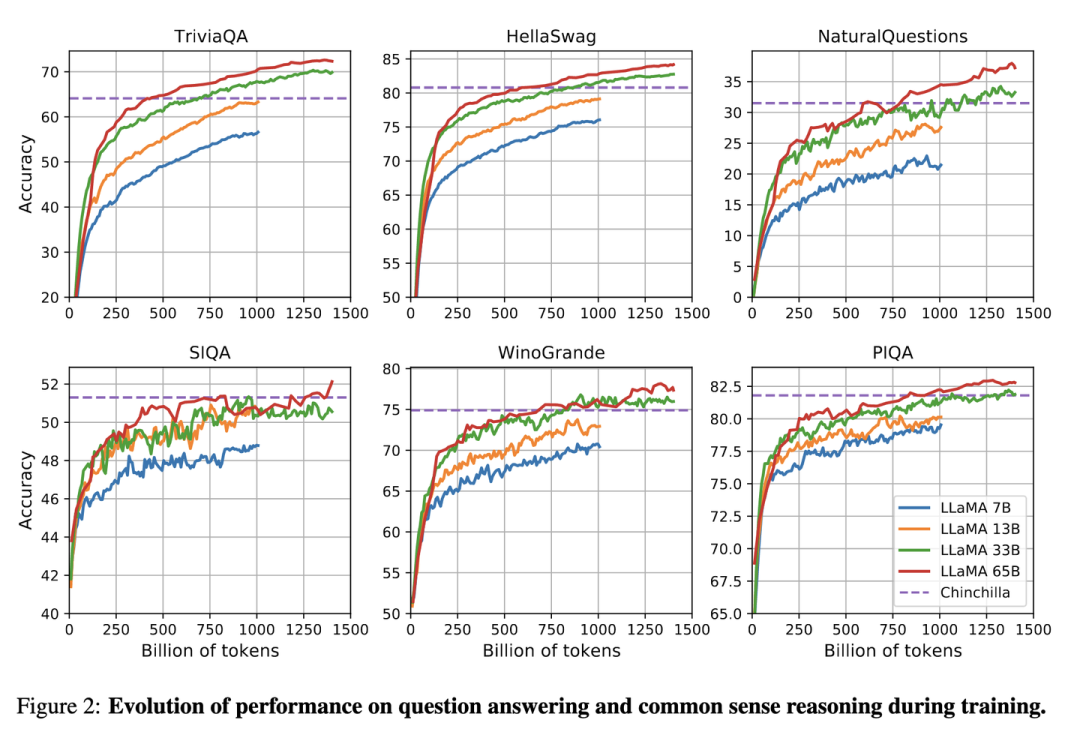
Meta在LLaMA[8]的觀點是:給定模型的目標性能,并不需要用最優的計算效率在最快時間訓練好模型,而應該在更大規模的數據上,訓練一個相對更小模型,這樣的模型在推理階段的成本更低,盡管訓練階段的效率不是最優的(同樣的算力其實能獲得更優的模型,但是模型尺寸也會更大)。根據Scaling Law,10B模型只需要200B的數據,但是作者發現7B的模型性能在1T的數據后還能繼續提升。

所以LLaMA工作的重點是訓練一系列語言模型,通過使用更多的數據,讓模型在有限推理資源下有最佳的性能。
具體而言,確定模型尺寸后,Scaling Law給到的只是最優的數據量,或者說是一個至少的數據量,實際在訓練中觀察在各個指標上的性能表現,只要還在繼續增長,就可以持續增加訓練數據。
審核編輯:黃飛
-
GPT
+關注
關注
0文章
354瀏覽量
15437 -
OpenAI
+關注
關注
9文章
1100瀏覽量
6580 -
大模型
+關注
關注
2文章
2491瀏覽量
2867
原文標題:大模型中的Scaling Law計算方法
文章出處:【微信號:zenRRan,微信公眾號:深度學習自然語言處理】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
FFTC問題求解答!!!動態scaling
多電機數學模型推導
電動助力轉向EPS——理論公式推導及simulink模型
電機控制系統基于概念的仿真模型
常用的feature scaling方法都有哪些?
EDA探索之MOSFET的微縮- Moore’s Law介紹
Scaling Law大模型設計實操案例

電感等效模型阻抗公式推導
張宏江深度解析:大模型技術發展的八大觀察點

浪潮信息趙帥:開放計算創新 應對Scaling Law挑戰

復旦提出大模型推理新思路:Two-Player架構打破自我反思瓶頸





 大模型的Scaling Law的概念和推導
大模型的Scaling Law的概念和推導










評論