寫在前面
Feature scaling,常見的提法有“特征歸一化”、“標準化”,是數據預處理中的重要技術,有時甚至決定了算法能不能work以及work得好不好。談到feature scaling的必要性,最常用的2個例子可能是:
特征間的單位(尺度)可能不同,比如身高和體重,比如攝氏度和華氏度,比如房屋面積和房間數,一個特征的變化范圍可能是[1000, 10000],另一個特征的變化范圍可能是[?0.1,0.2],在進行距離有關的計算時,單位的不同會導致計算結果的不同,尺度大的特征會起決定性作用,而尺度小的特征其作用可能會被忽略,為了消除特征間單位和尺度差異的影響,以對每維特征同等看待,需要對特征進行歸一化。
原始特征下,因尺度差異,其損失函數的等高線圖可能是橢圓形,梯度方向垂直于等高線,下降會走zigzag路線,而不是指向local minimum。通過對特征進行zero-mean and unit-variance變換后,其損失函數的等高線圖更接近圓形,梯度下降的方向震蕩更小,收斂更快,如下圖所示,圖片來自Andrew Ng。
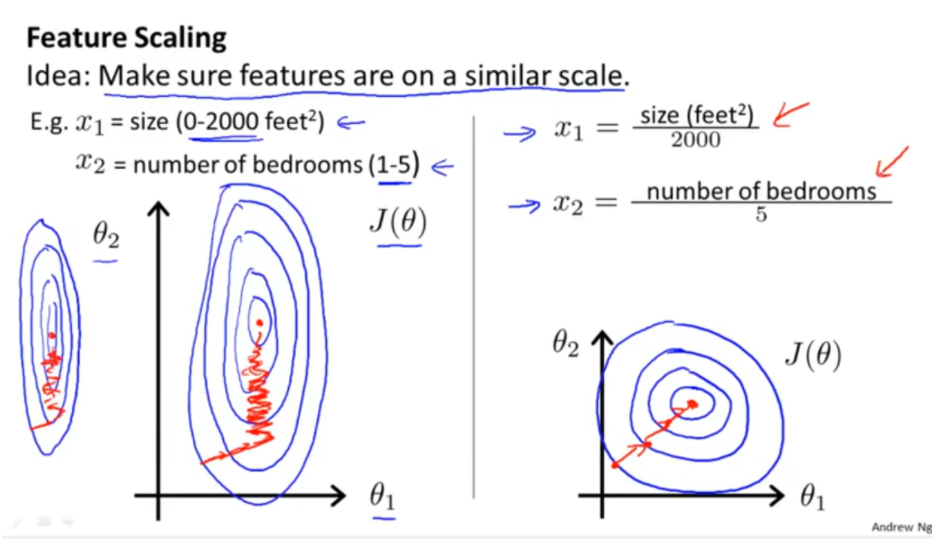
Feature Scaling from Andrew Ng 對于feature scaling中最常使用的Standardization,似乎“無腦上”就行了,本文想多探究一些為什么,
常用的feature scaling方法都有哪些?
什么情況下該使用什么feature scaling方法?有沒有一些指導思想?
所有的機器學習算法都需要feature scaling嗎?有沒有例外?
損失函數的等高線圖都是橢圓或同心圓嗎?能用橢圓和圓來簡單解釋feature scaling的作用嗎?
如果損失函數的等高線圖很復雜,feature scaling還有其他直觀解釋嗎?
根據查閱到的資料,本文將嘗試回答上面的問題。但筆者能力有限,空有困惑,能講到哪算哪吧(微笑)。
常用feature scaling方法
在問為什么前,先看是什么。 給定數據集,令特征向量為x,維數為D,樣本數量為R,可構成D×R的矩陣,一列為一個樣本,一行為一維特征,如下圖所示,圖片來自Hung-yi Lee pdf-Gradient Descent:
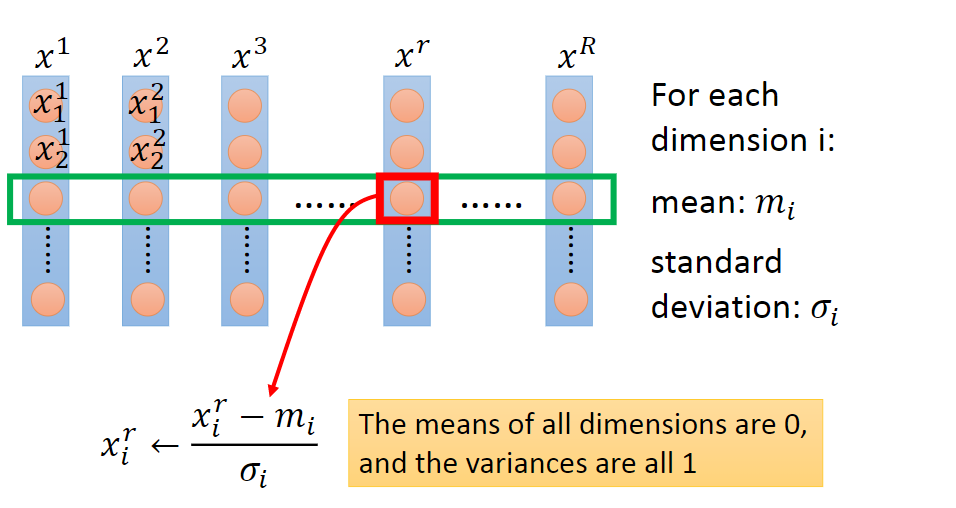
feature matrix feature scaling的方法可以分成2類,逐行進行和逐列進行。逐行是對每一維特征操作,逐列是對每個樣本操作,上圖為逐行操作中特征標準化的示例。 具體地,常用feature scaling方法如下,來自wiki,
Rescaling (min-max normalization、range scaling):
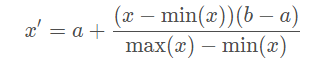
將每一維特征線性映射到目標范圍[a,b],即將最小值映射為a,最大值映射為b,常用目標范圍為[0,1]和[?1,1],特別地,映射到[0,1]計算方式為:
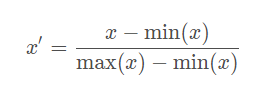
Mean normalization:
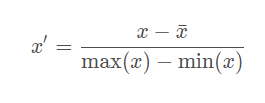
將均值映射為0,同時用最大值最小值的差對特征進行歸一化,一種更常見的做法是用標準差進行歸一化,如下。
Standardization (Z-score Normalization):
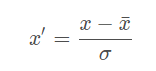 每維特征0均值1方差(zero-mean and unit-variance)。
每維特征0均值1方差(zero-mean and unit-variance)。
Scaling to unit length:
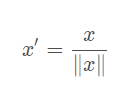 將每個樣本的特征向量除以其長度,即對樣本特征向量的長度進行歸一化,長度的度量常使用的是L2 norm(歐氏距離),有時也會采用L1 norm,不同度量方式的一種對比可以參見論文“CVPR2005-Histograms of Oriented Gradients for Human Detection”。 上述4種feature scaling方式,前3種為逐行操作,最后1種為逐列操作。容易讓人困惑的一點是指代混淆,Standardization指代比較清晰,但是單說Normalization有時會指代min-max normalization,有時會指代Standardization,有時會指代Scaling to unit length。
將每個樣本的特征向量除以其長度,即對樣本特征向量的長度進行歸一化,長度的度量常使用的是L2 norm(歐氏距離),有時也會采用L1 norm,不同度量方式的一種對比可以參見論文“CVPR2005-Histograms of Oriented Gradients for Human Detection”。 上述4種feature scaling方式,前3種為逐行操作,最后1種為逐列操作。容易讓人困惑的一點是指代混淆,Standardization指代比較清晰,但是單說Normalization有時會指代min-max normalization,有時會指代Standardization,有時會指代Scaling to unit length。
計算方式上對比分析
前3種feature scaling的計算方式為減一個統計量再除以一個統計量,最后1種為除以向量自身的長度。
減一個統計量可以看成選哪個值作為原點,是最小值還是均值,并將整個數據集平移到這個新的原點位置。如果特征間偏置不同對后續過程有負面影響,則該操作是有益的,可以看成是某種偏置無關操作;如果原始特征值有特殊意義,比如稀疏性,該操作可能會破壞其稀疏性。
除以一個統計量可以看成在坐標軸方向上對特征進行縮放,用于降低特征尺度的影響,可以看成是某種尺度無關操作。縮放可以使用最大值最小值間的跨度,也可以使用標準差(到中心點的平均距離),前者對outliers敏感,outliers對后者影響與outliers數量和數據集大小有關,outliers越少數據集越大影響越小。
除以長度相當于把長度歸一化,把所有樣本映射到單位球上,可以看成是某種長度無關操作,比如,詞頻特征要移除文章長度的影響,圖像處理中某些特征要移除光照強度的影響,以及方便計算余弦距離或內積相似度等。
稀疏數據、outliers相關的更多數據預處理內容可以參見scikit learn-5.3. Preprocessing data。 從幾何上觀察上述方法的作用,圖片來自CS231n-Neural Networks Part 2: Setting up the Data and the Loss,zero-mean將數據集平移到原點,unit-variance使每維特征上的跨度相當,圖中可以明顯看出兩維特征間存在線性相關性,Standardization操作并沒有消除這種相關性。
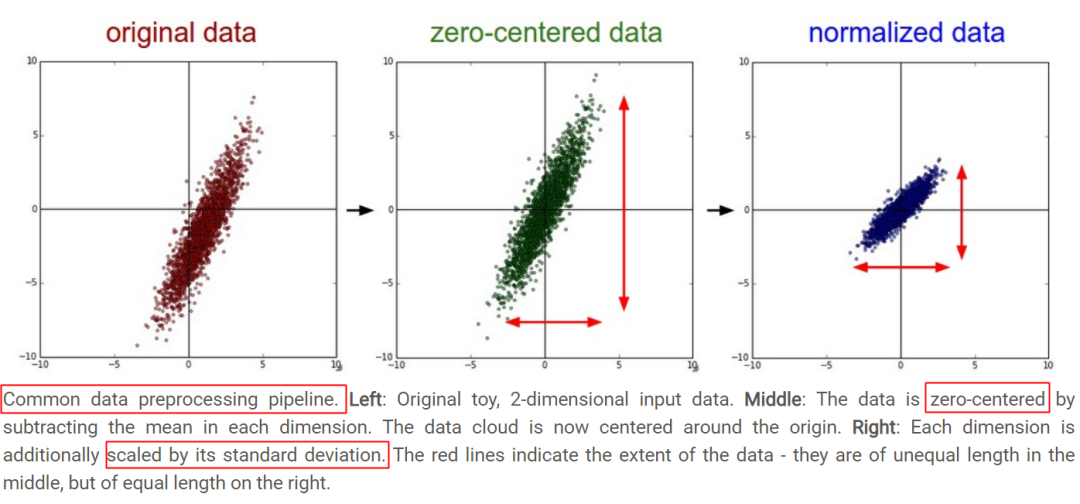
Standardization 可通過PCA方法移除線性相關性(decorrelation),即引入旋轉,找到新的坐標軸方向,在新坐標軸方向上用“標準差”進行縮放,如下圖所示,圖片來自鏈接,圖中同時描述了unit length的作用——將所有樣本映射到單位球上。
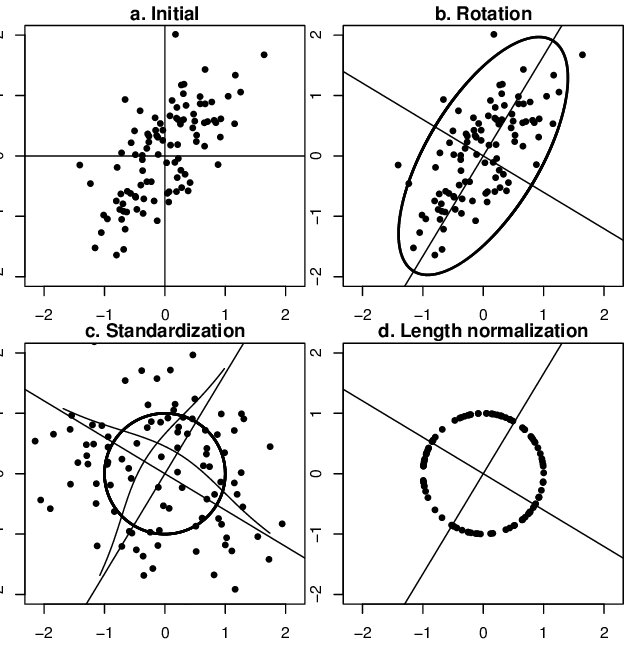
Effect of the operations of standardization and length normalization 當特征維數更多時,對比如下,圖片來自youtube,
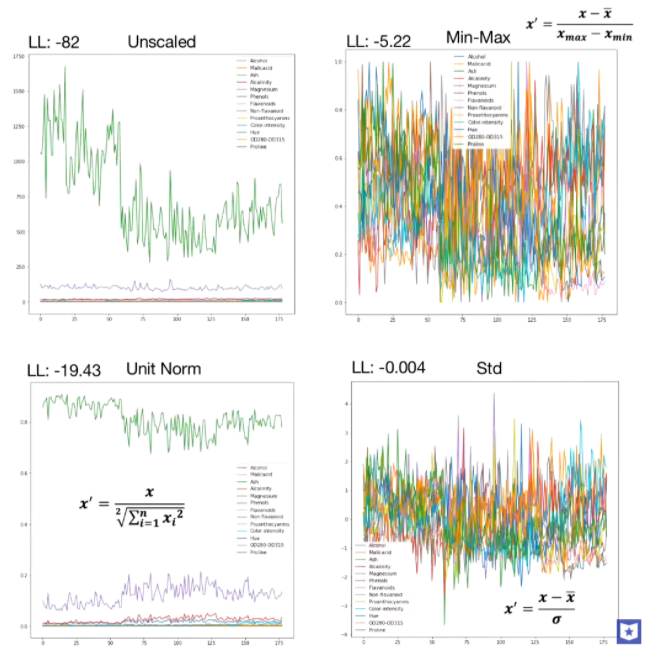
feature scaling comparison 總的來說,歸一化/標準化的目的是為了獲得某種“無關性”——偏置無關、尺度無關、長度無關……當歸一化/標準化方法背后的物理意義和幾何含義與當前問題的需要相契合時,其對解決該問題就有正向作用,反之,就會起反作用。所以,“何時選擇何種方法”取決于待解決的問題,即problem-dependent。
feature scaling 需要還是不需要
下圖來自data school-Comparing supervised learning algorithms,對比了幾個監督學習算法,最右側兩列為是否需要feature scaling。
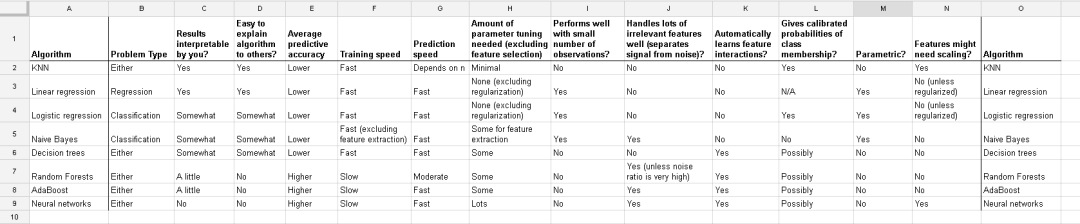
Comparing supervised learning algorithms 下面具體分析一下。
什么時候需要feature scaling?
涉及或隱含距離計算的算法,比如K-means、KNN、PCA、SVM等,一般需要feature scaling,因為:
zero-mean一般可以增加樣本間余弦距離或者內積結果的差異,區分力更強,假設數據集集中分布在第一象限遙遠的右上角,將其平移到原點處,可以想象樣本間余弦距離的差異被放大了。在模版匹配中,zero-mean可以明顯提高響應結果的區分度。 就歐式距離而言,增大某個特征的尺度,相當于增加了其在距離計算中的權重,如果有明確的先驗知識表明某個特征很重要,那么適當增加其權重可能有正向效果,但如果沒有這樣的先驗,或者目的就是想知道哪些特征更重要,那么就需要先feature scaling,對各維特征等而視之。 增大尺度的同時也增大了該特征維度上的方差,PCA算法傾向于關注方差較大的特征所在的坐標軸方向,其他特征可能會被忽視,因此,在PCA前做Standardization效果可能更好,如下圖所示,圖片來自scikit learn-Importance of Feature Scaling,
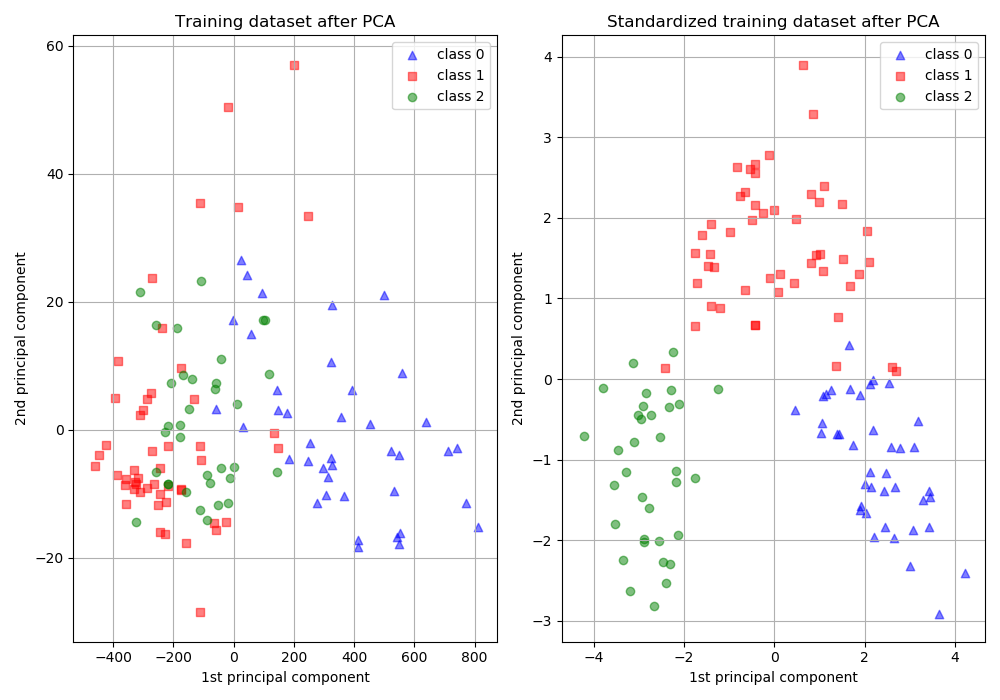
PCA and Standardization
損失函數中含有正則項時,一般需要feature scaling:對于線性模型y=wx+b而言,x的任何線性變換(平移、放縮),都可以被w和b“吸收”掉,理論上,不會影響模型的擬合能力。但是,如果損失函數中含有正則項,如λ∣∣w∣∣^2,λ為超參數,其對w的每一個參數施加同樣的懲罰,但對于某一維特征xi而言,其scale越大,系數wi越小,其在正則項中的比重就會變小,相當于對wi懲罰變小,即損失函數會相對忽視那些scale增大的特征,這并不合理,所以需要feature scaling,使損失函數平等看待每一維特征。
梯度下降算法,需要feature scaling。梯度下降的參數更新公式如下,
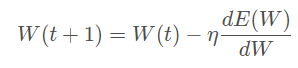
E(W)為損失函數,收斂速度取決于:參數的初始位置到local minima的距離,以及學習率η的大小。一維情況下,在local minima附近,不同學習率對梯度下降的影響如下圖所示:
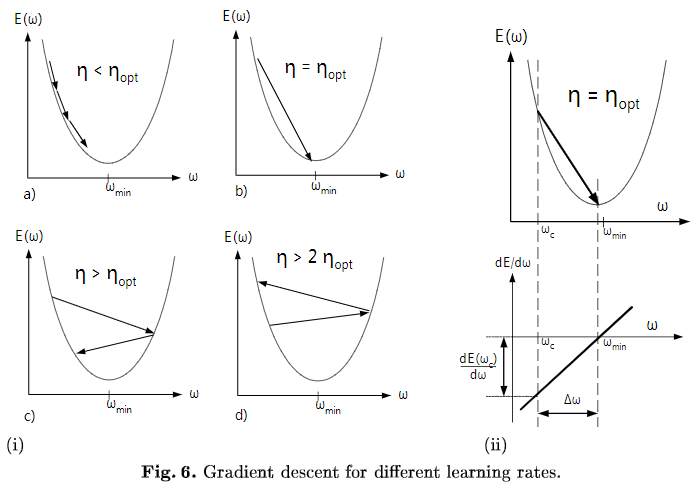
Gradient descent for different learning rates 多維情況下可以分解成多個上圖,每個維度上分別下降,參數W為向量,但學習率只有1個,即所有參數維度共用同一個學習率(暫不考慮為每個維度都分配單獨學習率的算法)。收斂意味著在每個參數維度上都取得極小值,每個參數維度上的偏導數都為0,但是每個參數維度上的下降速度是不同的,為了每個維度上都能收斂,學習率應取所有維度在當前位置合適步長中最小的那個。下面討論feature scaling對gradient descent的作用,
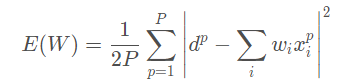
不同方向上的下降速度變化不同(二階導不同,曲率不同),恰由輸入的協方差矩陣決定,通過scaling改變了損失函數的形狀,減小不同方向上的曲率差異。將每個維度上的下降分解來看,給定一個下降步長,如果不夠小,有的維度下降的多,有的下降的少,有的還可能在上升,損失函數的整體表現可能是上升也可能是下降,就會不穩定。scaling后不同方向上的曲率相對更接近,更容易選擇到合適的學習率,使下降過程相對更穩定。
zero center與參數初始化相配合,縮短初始參數位置與local minimum間的距離,加快收斂。模型的最終參數是未知的,所以一般隨機初始化,比如從0均值的均勻分布或高斯分布中采樣得到,對線性模型而言,其分界面初始位置大致在原點附近,bias經常初始化為0,則分界面直接通過原點。同時,為了收斂,學習率不會很大。而每個數據集的特征分布是不一樣的,如果其分布集中且距離原點較遠,比如位于第一象限遙遠的右上角,分界面可能需要花費很多步驟才能“爬到”數據集所在的位置。所以,無論什么數據集,先平移到原點,再配合參數初始化,可以保證分界面一定會穿過數據集。此外,outliers常分布在數據集的外圍,與分界面從外部向內挪動相比,從中心區域開始挪動可能受outliers的影響更小。
對于采用均方誤差損失LMS的線性模型,損失函數恰為二階,如下圖所示
另有從Hessian矩陣特征值以及condition number角度的理解,詳見Lecun paper-Efficient BackProp中的Convergence of Gradient Descent一節,有清晰的數學描述,同時還介紹了白化的作用——解除特征間的線性相關性,使每個維度上的梯度下降可獨立看待。
文章開篇的橢圓形和圓形等高線圖,僅在采用均方誤差的線性模型上適用,其他損失函數或更復雜的模型,如深度神經網絡,損失函數的error surface可能很復雜,并不能簡單地用橢圓和圓來刻畫,所以用它來解釋feature scaling對所有損失函數的梯度下降的作用,似乎過于簡化,見Hinton vedio-3.2 The error surface for a linear neuron。
對于損失函數不是均方誤差的情況,只要權重w與輸入特征x間是相乘關系,損失函數對w的偏導必然含有因子x,w的梯度下降速度就會受到特征x尺度的影響。理論上為每個參數都設置上自適應的學習率,可以吸收掉x尺度的影響,但在實踐中出于計算量的考慮,往往還是所有參數共用一個學習率,此時x尺度不同可能會導致不同方向上的下降速度懸殊較大,學習率不容易選擇,下降過程也可能不穩定,通過scaling可對不同方向上的下降速度有所控制,使下降過程相對更穩定。
對于傳統的神經網絡,對輸入做feature scaling也很重要,因為采用sigmoid等有飽和區的激活函數,如果輸入分布范圍很廣,參數初始化時沒有適配好,很容易直接陷入飽和區,導致梯度消失,所以,需要對輸入做Standardization或映射到[0,1]、[?1,1],配合精心設計的參數初始化方法,對值域進行控制。但自從有了Batch Normalization,每次線性變換改變特征分布后,都會重新進行Normalization,似乎可以不太需要對網絡的輸入進行feature scaling了?但習慣上還是會做feature scaling。
什么時候不需要Feature Scaling?
與距離計算無關的概率模型,不需要feature scaling,比如Naive Bayes; 與距離計算無關的基于樹的模型,不需要feature scaling,比如決策樹、隨機森林等,樹中節點的選擇只關注當前特征在哪里切分對分類更好,即只在意特征內部的相對大小,而與特征間的相對大小無關。
小結
這篇文章寫得十分艱難,一開始以為蠻簡單直接,但隨著探索的深入,冒出的問號越來越多,打破了很多原來的“理所當然”,所以,在寫的過程中不停地做加法,很多地方想解釋得盡量直觀,又不想照搬太多公式,但自己的理解又不夠深刻,導致現在敘述這么冗長,希望以后在寫文時能更專注更精煉。
審核編輯 :李倩
-
算法
+關注
關注
23文章
4629瀏覽量
93196 -
函數
+關注
關注
3文章
4345瀏覽量
62882
原文標題:小結
文章出處:【微信號:vision263com,微信公眾號:新機器視覺】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
Jtti:常用的網絡質量監控方法有哪些
常用的devops工具集成方法
電源常用ic腳位解析方法 7腳電源芯片怎么看型號
浪潮信息趙帥:開放計算創新 應對Scaling Law挑戰

我常用的分析方法——輸入輸出阻抗,是怎么玩的?你會不?
圖像識別算法都有哪些方法
電磁仿真軟件有哪些常用的方法
smt貼片加工常用的檢測修理方法有哪些
常用的無損檢測方法有哪些?主要應用如何?
示波器探頭常用的校準方法
自動焊常用的焊接方法有哪些





 常用的feature scaling方法都有哪些?
常用的feature scaling方法都有哪些?










評論