在用電路實現加法之后,就需要一個能把結果保存下來的存儲電路。設想存儲電路的運行邏輯是:有一個控制開關,當著開關=1的時候,輸出端等于輸入端的值,當開關=0的時候,輸入端的值的變化,不影響輸出端的值,也就是輸出端保持之前的數值。
4.1. 一位觸發器
首先我們得承認,要像上一章的加法器一樣,通過邏輯分析設計這樣一個能滿足存儲數字需求的電路不是一件很容易的事情,本章拿前人的成果,直接把電路給出來,試著給大家分析。
1918年英國工程師埃克爾斯發明了一個具有記憶功能的電路,如圖 4-1:
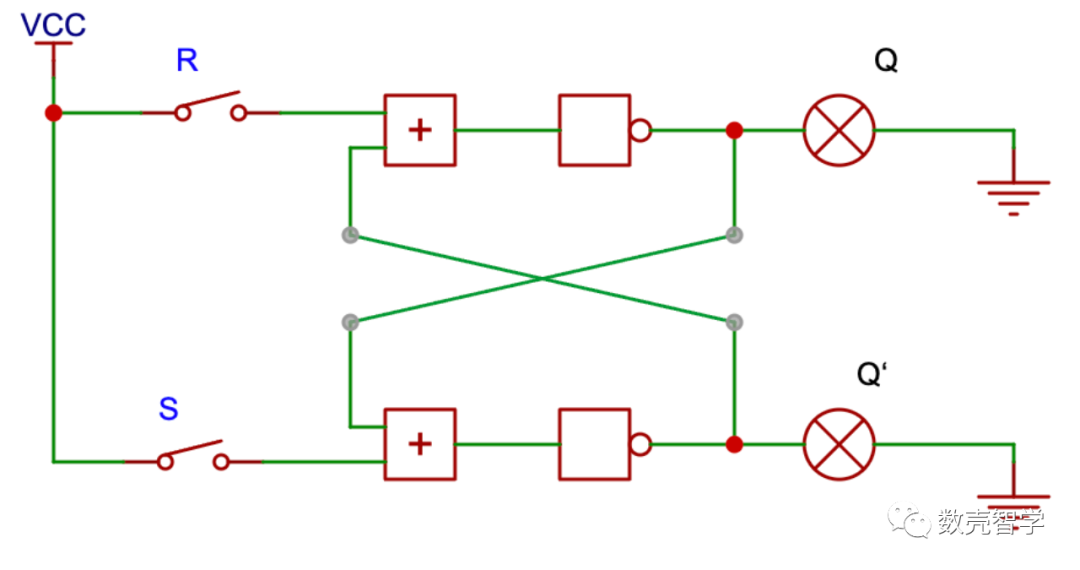
圖 4-1具有記憶能力的電路(觸發器)
這是一個震蕩反饋電路,對于初學者來說稍微有點燒腦,我們列出這個電路的真值表(表 4-1):
表 4-1 觸發器的輸入輸出真值表
| S | R | Q | |
|---|---|---|---|
| 0 | 0 | 不變 | 不變 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
我們可以發現該電路最神奇的地方在于當S=R=0的時候,可以保持輸出的值Q不變,即這個時候Q的值不受R的變化影響,也就是Q能夠保存一個比特的信號,這就是使得其具有作為存儲電路的可能性。
仔細分析這個表的輸入輸出,可以發現幾個有意思的特征可以被利用:
1、如果另S和R保持相反的輸入(即R=0,S=1 或者R=1,S=0),則輸出Q的值一直和R保持一致;
2、如果S=R=1,輸出Q=0;S=R=0,輸出Q保存一個比特信號;
在此技術上,我們稍微修改一下電路
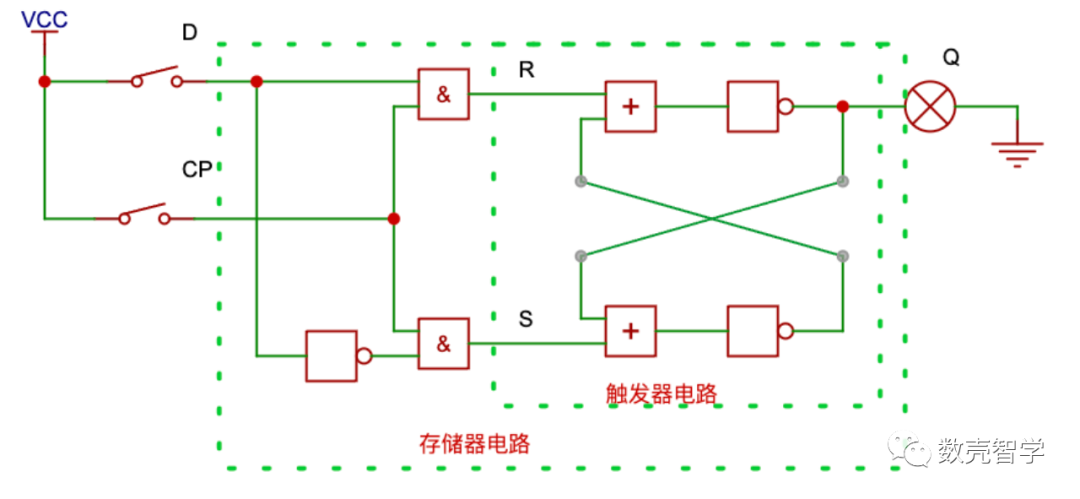
圖 4-2一位寄存器比特單元電路
在圖 4-1的基礎上,在S、R兩個輸入端分別增加一個“與門”,用CP開關進行控制,根據表 4-1,電路邏輯狀態如下:
當CP=0,無論開關D=0還是D=1,通過兩個與門的作用,S=R=0,Q保持之前的值不變,起到保存比特信號的效果;
當CP=1,S、R的值取決于開關D的狀態,D=1,則S=1、R=0、輸出Q=D=1,相反D=0,則S=0、R=1、輸出Q=D=0,也就是該狀態下,存儲器可以把輸入的值寫入到Q。
至此,一個完整的一位存儲電路設計完成了,CP是狀態控制開關,CP=1,使得輸出Q=輸入D;CP=0,輸出狀態不變,實現存儲。
圖 4-2是完整的一位存儲電路,大虛線框代表的就是存儲電路,用簡化的圖例可以表示為:

圖 4-3觸發器示意圖
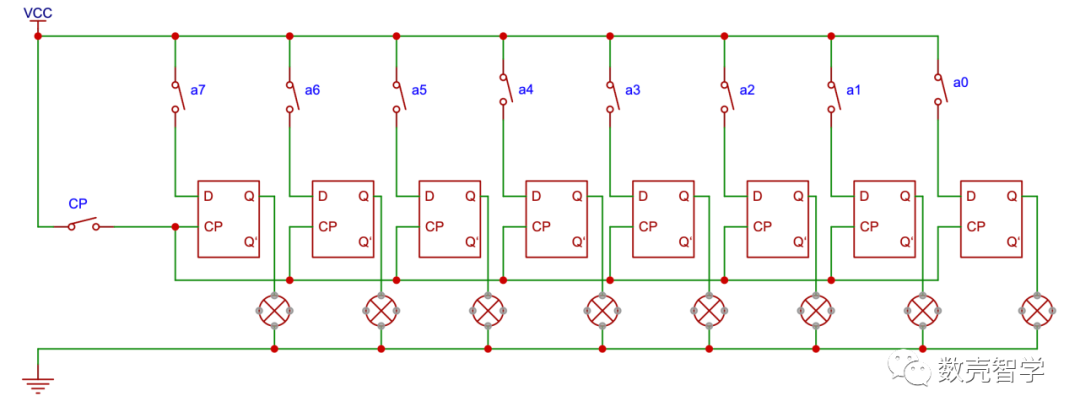
圖 4-4 八位二進制數字存儲
4.2. 存儲芯片設計
圖 4-2的電路輸入、輸出在不同的線路端,對于存儲芯片的使用來說還是不夠方便。作為存儲芯片,我們希望寫入和讀取是同一個端口,用寫入(W)、讀取(R)兩個控制端決定當前是處于讀取還是寫入狀態,這樣的設計更有利于大規模的存儲電路的堆疊。

圖 4-5 比特存儲單元電路
圖 4-5中把寄存器單元的輸出Q和“讀”控制開關R通過“與門”G連接,輸出端和輸入端D連接。當R斷開狀態,G與DB端的連線相當于斷開,使得寄存器輸出端Q不對DB端的狀態造成影響。工作步驟如下:
1、W合并,R斷開,寫入狀態:Q=DB
2、W斷開,R斷開,保持狀態:Q不受DB影響;
3、W斷開,R合并,讀取狀態:DB=Q
至此,我們完成存儲芯片的比特單元的電路設計,用更簡單的示意圖表示如下:

圖 4-6比特存儲單元電路示意圖

圖 4-7 八位存儲芯片單元(寄存器)電路圖
現在我們已經可以嘗試站在軟件開發的角度對存儲芯片的電路設計提一些需求,把圖 4-7的8位整體作為一個字節的存儲單元,一個存儲芯片有大量的字節存儲單元(比如現在主流的8G內存有810241024個這樣的字節存儲單元),希望給每個存儲單元一個位置編號,方便在編程的時候直接定位存儲的位置,這個位置編號成為“地址”。
圖 4-7的簡化示意圖如下:

圖 4-8 八位寄存器示意圖
為了方便理解,先給出一個字節存儲單元疊在一起的電路圖(圖 4-9)作為過度,從圖中可以看出,默認狀態所有的讀、寫控制都斷開,當需要對第一行進行“存”操作,只需要把W0=1,該狀態下D0~D7修改的值都會被保存到第一行的8個電路中。

圖 4-9 四組八位存儲芯片字節單元組電路圖
這個電路與我們的存儲芯片越來越接近了,但是還有一個缺點,每行都需要W、R兩個控制端,那么一個保存256字節的存儲芯片就有256*2個控制端,而且,隨著存儲芯片的容量越來越大,控制端越來越多,如果封裝成一個芯片不可能設置那么多的針腳,所以必須想到變通的方法。
觀察發現,雖然W、R控制端總數很多,但是在存儲芯片操作的過程中,每次只會對其中的一行(一個字節)操作。我們需要一個地址選擇功能的電路,通過輸入n位的數字,能夠實現在2^n^個地址中選中一個。因為n位的二進制數字能表示0~2^n-1^的數字,才提出這么精準的設計需求。
有一種叫“譯碼器”的電路邏輯,解決了這種問題。我們用一個2進4出的譯碼器電路來演示說明其原理,方法類似設計加法器電路(圖 3-3)設計的方法:
1、列出所有可能的邏輯表達值(表 4-2);
表 4-2 二進四出譯碼器邏輯真值表
| A1 | A0 | D3 | D2 | D1 | D0 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 |
2、根據真值表給出邏輯表達式;

3、根據邏輯表達式設計譯碼器的電路圖

圖 4-10 二進4出譯碼器電路圖
三進八出譯碼器的示意圖如下:

圖 4-11三進八出譯碼器示意圖
將譯碼器連接到字節單元組存儲(圖 4-9)的所有W、R端口(如圖 4-12)。當A1=0,A0=1,通過譯碼器D1=1,W1通過與門連接D1和W(W1=D1&W),R1通過與門連接D1和R(R1=D1&R)。所以譯碼器控制了選中哪一行的存儲單元,W、R實現對這行存儲單元的讀、寫控制。
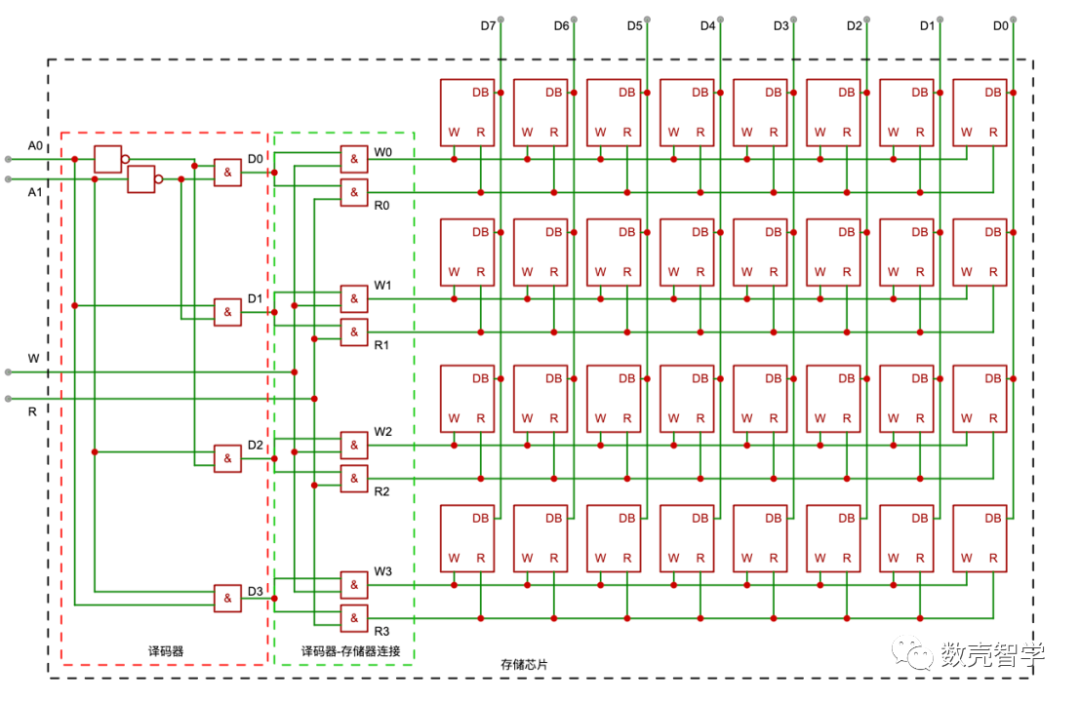
圖 4-12連接譯碼器后的完整存儲電路
圖 4-12中利用2比特位的譯碼器實現了4行(4字節)的存儲芯片,同理,可以用8比特位的譯碼器實現256行(256字節)的存儲芯片。
這里的2比特位和8比特位即內存地址長度,現在計算機的操作系統常用32位和64位,指的就是內存的地址長度。按照這樣的理解32位的操作,最長控制4294967296個地址,因為每個地址所代表的內存空間也是32位(4個字節),可以說其能控制的最大存儲是:4294967296 * 4字節 = 16GB。當然現代計算機還可以通過譯碼器的級聯擴展地址空間。
為了下文繪制電路圖方便,把圖 4-12簡化成表示8位地址的內存示意圖(圖 4-13):

圖 4-13 八位地址的內存示意圖
-
寄存器
+關注
關注
31文章
5363瀏覽量
120949 -
存儲電路
+關注
關注
2文章
11瀏覽量
13143 -
加法器
+關注
關注
6文章
183瀏覽量
30186 -
觸發器
+關注
關注
14文章
2003瀏覽量
61289
發布評論請先 登錄
相關推薦




 存儲電路實現原理詳解
存儲電路實現原理詳解










評論