怎么增加差分對的線性范圍?
差分算法是一種常用的計算機算法,用于解決序列上的差的問題。差分對的線性范圍是指一段序列中存在的差分對的數量的線性增長范圍。在本文中,我們將探討如何增加差分對的線性范圍。
差分算法的基本原理是將一個序列中的相鄰元素的差值存儲在另一個數組中。這個數組稱為差分數組,它的長度比原序列少1。通過這種方法,我們可以在O(1)的時間復雜度內對序列進行更改操作,而不必重新計算整個序列的值。
差分算法的應用非常廣泛,它可以用于解決排序問題、數組區間修改問題、連通性問題等。其中,最常見的應用場景是數組區間修改問題。例如,給定一個長度為n的數組A和一個包含m個修改操作的序列,每個操作包含一個左端點l和右端點r以及一個修正值v。我們需要對數組A進行m次修改操作后,計算A中任意一段區間的和。
假設我們有一個差分數組D,它的第i個元素是A[i]-A[i-1],即原數組的相鄰元素之差。那么,區間[l,r]的和就可以通過下面的公式計算得出:
sum[l,r] = A[l] + D[l+1] + D[l+2] + ... + D[r]
通過這種方法,我們只需要修改差分數組D就可以對原數組進行區間修改操作,并且時間復雜度是O(1)。
現在我們來考慮如何增加差分對的線性范圍。首先,我們需要了解差分對的定義。一個差分對是指數組D中相鄰元素之差為正數的一對位置。例如,對于差分數組D=[1, 2, -3, -1, 4],它包含兩個差分對(1,2)和(4,5)。
增加差分對的線性范圍的方法有很多種,下面我們將介紹其中的兩種方法。
方法一:增加原序列中的冗余元素
要增加差分對的線性范圍,我們可以將原序列中的冗余元素添加到末尾。例如,假設原序列為A=[3, 1, 4, 6, 7],我們可以將它擴展為A'=[3, 1, 4, 6, 7, 0, 0, 0, ...],然后對它進行差分運算得到差分數組D=[3, -2, 3, 2, -7, 0, 0, 0, ...]。這個差分數組包含了更多的正數和負數,因此它的線性范圍更大。
由于我們需要將冗余元素添加到末尾,因此這種方法的時間復雜度是O(n)。實現時需要注意,擴展后的數組長度必須是2的冪次方,可以通過在數組末尾添加一些值為0的元素來實現這一點。
方法二:應用四邊形不等式
四邊形不等式是一個重要的算法原理,它可以用于優化區間加法操作的時間復雜度。在差分算法中,我們也可以應用這個原理來增加差分對的線性范圍。
假設我們需要對原序列進行n次修改操作,并且每個操作的修改值都相同。我們可以將這些操作分為若干個塊,每個塊包含k個連續的操作。通過計算差分數組D中每個塊的偏差,我們可以將序列的修改操作轉換為每個塊的加法操作。例如,對于原序列A=[3, 1, 4, 6, 7],差分數組D=[3, -2, 3, 2, -7],我們可以將它分為兩個塊,每個塊包含3個操作。第一個塊對應的偏差為D[1]+D[2]+D[3]=-2,因此我們可以將它轉換為A[2],A[3],A[4]的加法操作,即A[2]+=v,A[3]+=v,A[4]+=v。第二個塊對應的偏差為D[4]+D[5]=-7,因此我們可以將它轉換為A[5],A[6],A[7]的加法操作,即A[5]+=v,A[6]+=v,A[7]+=v。
通過應用四邊形不等式,我們可以將每個塊的加法操作轉換為兩個加法操作,在這個過程中引入一些冗余元素。例如,對于上面的例子,我們可以將第一個塊的加法操作轉換為A[2]+=v,A[3]+=v,A[4]+=v,A[5]-=v,A[6]-=v,A[7]-=v,這樣可以增加兩個差分對(2,3)和(5,6)。通過這種方法,我們可以將差分對的線性范圍增加到O(n/log n)。
總結
在本文中,我們探討了如何增加差分對的線性范圍。通過增加原序列中的冗余元素和應用四邊形不等式,我們可以在不增加時間復雜度的情況下增加差分對的數量。這些方法在實際應用中非常有用,可以幫助我們更快地解決實際問題。
-
差分對
+關注
關注
0文章
9瀏覽量
6870
發布評論請先 登錄
相關推薦
前端的audio codec輸出信號為R/L/GND, 如何變成差分對信號輸入TPA3113D2?
霍爾效應中uh和im的線性范圍
THS4524的差分輸入范圍是多少?
4芯M8接口的線性范圍是多少

LED汽車大燈-線性方案
如何對PCB進行差分對的走線操作呢?
差示掃描量熱儀測試范圍和工作原理

低壓差線性穩壓器電路圖分享
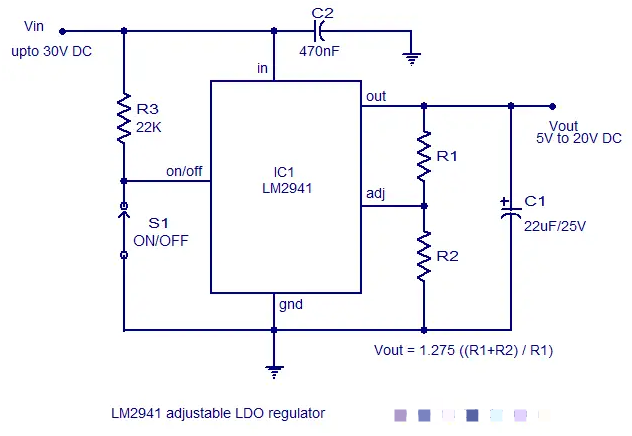
低壓差線性穩壓器的特點有哪些




 怎么增加差分對的線性范圍?
怎么增加差分對的線性范圍?












評論