常用的10個泰勒公式
泰勒公式是數學中的一個重要的工具,在數學物理學中有著廣泛的應用。它可以用于計算任意一點附近的函數近似值,是求解復雜問題的必備工具。以下是常用的10個泰勒公式:
1. 常數函數的泰勒公式
常數函數的泰勒公式非常簡單,因為常數函數在任何點的導數都為0,所以其泰勒展開式就是其自身。換句話說,對于任何實數c,我們有
f(x) = f(c)
這就是常數函數的泰勒公式。
2. 一階導數存在的函數的泰勒公式
對于一階導數存在的函數f(x),可以使用以下公式計算其在點a處的泰勒展開式:
f(x) = f(a) + f'(a)(x-a)
其中f'(a)表示在點a處的導數。
3. 二階導數存在的函數的泰勒公式
對于二階導數存在的函數f(x),可以使用以下公式計算其在點a處的泰勒展開式:
f(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2
其中f''(a)表示在點a處的二階導數。
4. 三階導數存在的函數的泰勒公式
對于三階導數存在的函數f(x),可以使用以下公式計算其在點a處的泰勒展開式:
f(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \frac{f'''(a)}{3!}(x-a)^3
其中f'''(a)表示在點a處的三階導數。
5. n階導數存在的函數的泰勒公式
對于n階導數存在的函數f(x),可以使用以下公式計算其在點a處的泰勒展開式:
f(x) = \sum_{k=0}^{n}\frac{f^{(k)}(a)}{k!}(x-a)^k
其中,f^{(k)}(a)表示在點a處的k階導數。
6. 正弦函數的泰勒公式
對于正弦函數,它在任何一點的值和導數都比較容易計算,所以它關于任意一點a的泰勒公式是:
\sin(x) = \sum_{k=0}^{\infty}\frac{(-1)^k}{(2k+1)!}(x-a)^{2k+1}
7. 余弦函數的泰勒公式
余弦函數也類似于正弦函數,其關于任意一點a的泰勒公式是:
\cos(x) = \sum_{k=0}^{\infty}\frac{(-1)^k}{(2k)!}(x-a)^{2k}
8. 指數函數的泰勒公式
指數函數是一個非常特殊的函數,我們可以證明它在任何點處的取值和導數都等于它在0點處的取值和導數。因此,它的泰勒公式也非常容易計算:
e^x = \sum_{k=0}^{\infty}\frac{x^k}{k!}
9. 對數函數的泰勒公式
對于對數函數,其泰勒公式與指數函數非常相似,但是要注意在x=0處不存在對數函數。因此:
\ln(x) = \ln(a) + \frac{x-a}{a} - \frac{(x-a)^2}{2a^2} + \frac{(x-a)^3}{3a^3} - ...
10. 雙曲函數的泰勒公式
雙曲函數包括雙曲正弦函數和雙曲余弦函數。它們的泰勒公式分別是:
\sinh(x) = \sum_{k=0}^{\infty}\frac{x^{2k+1}}{(2k+1)!}
\cosh(x) = \sum_{k=0}^{\infty}\frac{x^{2k}}{(2k)!}
這些公式是常用的泰勒公式,它們可以幫助我們快速地計算函數的近似值,進一步分析函數在某個點的性質。當然,我們在實際應用時,還需要考慮泰勒展開式的收斂性和誤差范圍等問題。
-
二階電路
+關注
關注
0文章
16瀏覽量
9844
發布評論請先 登錄
相關推薦
電工常用的計算公式
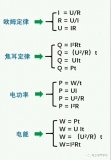
Aigtek功率放大器選型常用公式&概念總結

云端彈性計算公式有哪些內容?
平衡流量計計算公式

1pF-10pF的電容最大承受功率是多少?
微變等效電路rbe的計算公式
信噪比SNR、信號質量RSSI的定義及公式

電源設計的10個階段
《合宙的第一個10年》故事連載09:建立客戶信任還有公式?





 常用的10個泰勒公式
常用的10個泰勒公式











評論