transformer架構可能看起來很恐怖,您也可能在YouTube或博客中看到了各種解釋。但是,在我的博客中,我將通過提供一個全面的數學示例闡明它的原理。通過這樣做,我希望簡化對transformer架構的理解。 那就開始吧!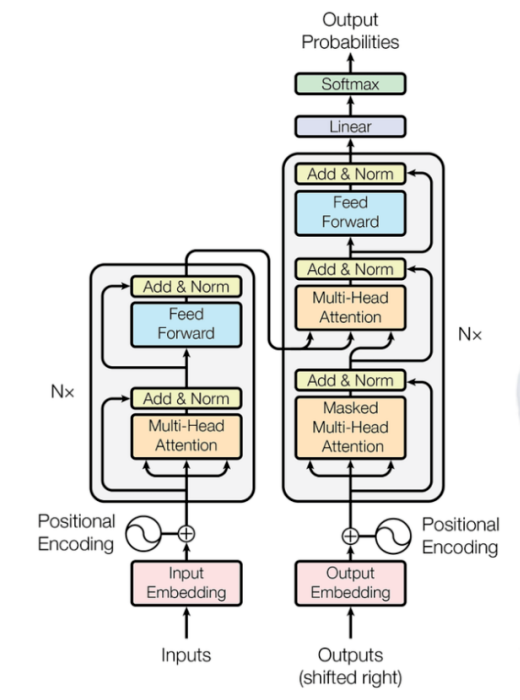
Inputs and Positional Encoding
讓我們解決最初的部分,在那里我們將確定我們的輸入并計算它們的位置編碼。
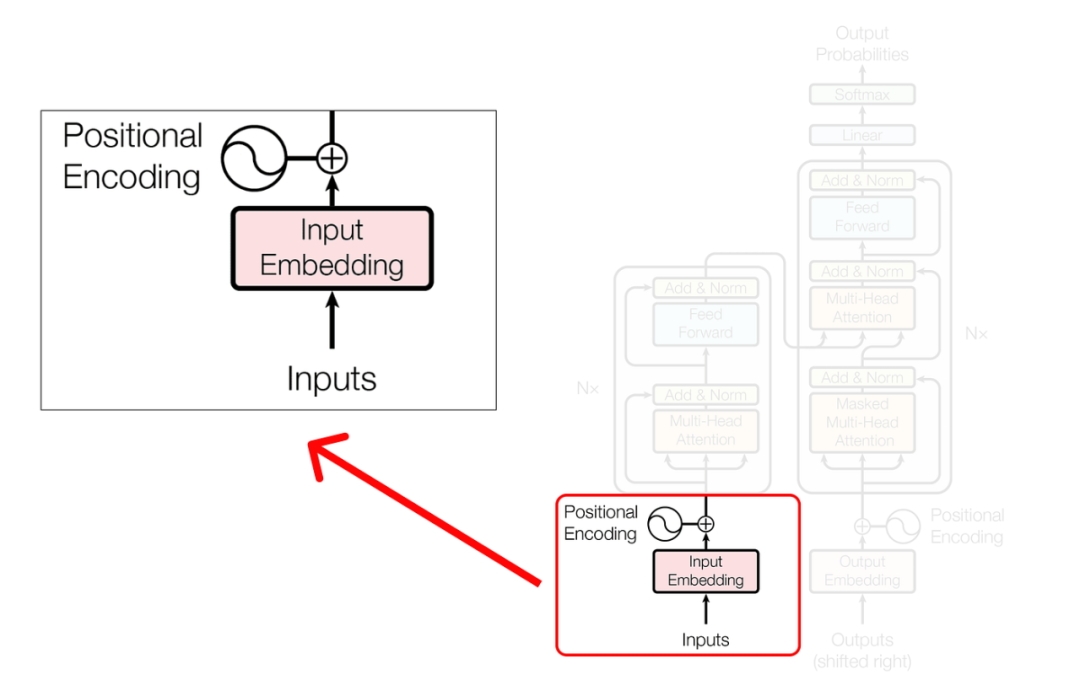
Step 1 (Defining the data)
第一步是定義我們的數據集(語料庫)。

在我們的數據集中,有3個句子(對話) 取自《權力的游戲》電視劇。盡管這個數據集看起來很小,但它已經足以幫助我們理解之后的數學公式。
Step 2 (Finding the Vocab Size)
為了確定詞匯量,我們需要確定數據集中的唯一單詞總數。這對于編碼(即將數據轉換為數字) 至關重要。 
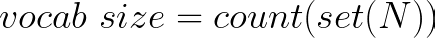 ? 其中N是所有單詞的列表,并且每個單詞都是單個token,我們將把我們的數據集分解為一個token列表,表示為N。
? 其中N是所有單詞的列表,并且每個單詞都是單個token,我們將把我們的數據集分解為一個token列表,表示為N。 

獲得token列表(表示為N) 后,我們可以應用公式來計算詞匯量。 具體公式原理如下: 

使用set操作有助于刪除重復項,然后我們可以計算唯一的單詞以確定詞匯量。因此,詞匯量為23,因為給定列表中有23個獨特的單詞。
Step 3 (Encoding and Embedding)
接下來為數據集的每個唯一單詞分配一個整數作為編號。
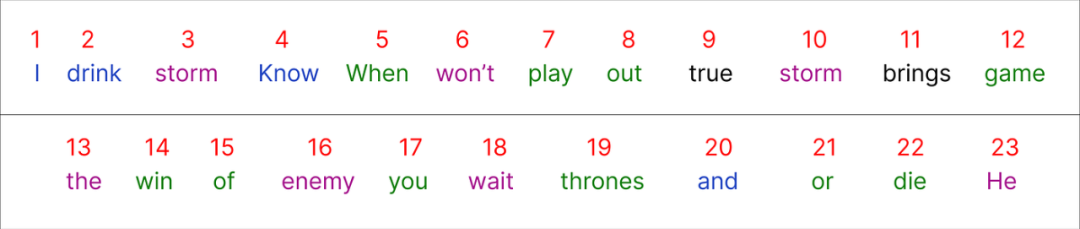
 在對我們的整個數據集進行編碼之后,是時候選擇我們的輸入了。我們將從語料庫中選擇一個句子以開始: ? “When you play game of thrones”
在對我們的整個數據集進行編碼之后,是時候選擇我們的輸入了。我們將從語料庫中選擇一個句子以開始: ? “When you play game of thrones” 
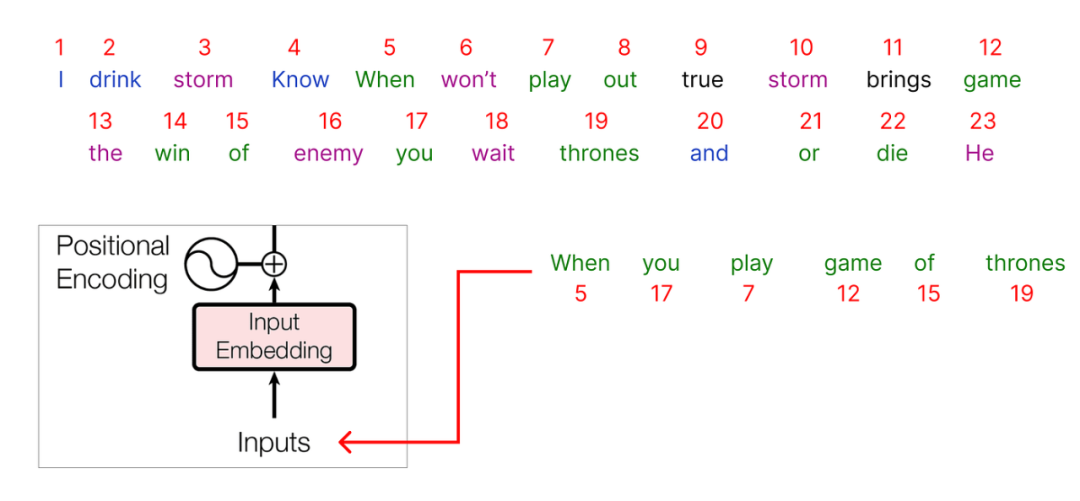
作為輸入傳遞的每個字將被表示為一個編碼,并且每個對應的整數值將有一個關聯的embedding聯系到它。 
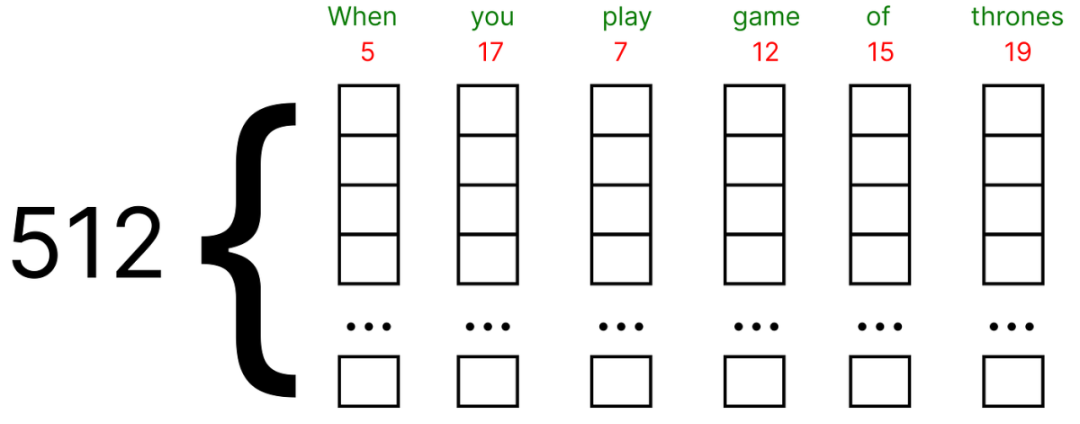
這些embedding可以使用谷歌Word2vec (單詞的矢量表示) 找到。在我們的數值示例中,我們將假設每個單詞的embedding向量填充有(0和1) 之間的隨機值。
此外,原始論文使用embedding向量的512維度,我們將考慮一個非常小的維度,即5作為數值示例。

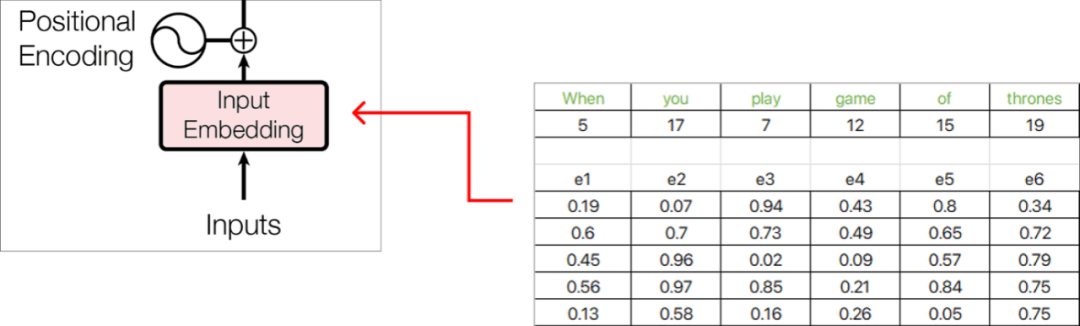
現在,每個單詞embedding都由5維的embedding向量表示,并使用Excel函數RAND() 用隨機數填充值。
Step 4 (Positional Embedding)
讓我們考慮第一個單詞,即“when”,并為其計算位置embedding向量。位置embedding有兩個公式:
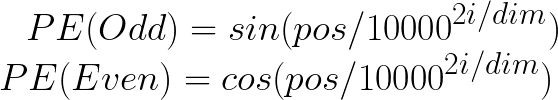
第一個單詞“when”的POS值將為零,因為它對應于序列的起始索引。此外,i的值(取決于是偶數還是奇數) 決定了用于計算PE值的公式。維度值表示embedding向量的維度,在我們的情形下,它是5。 
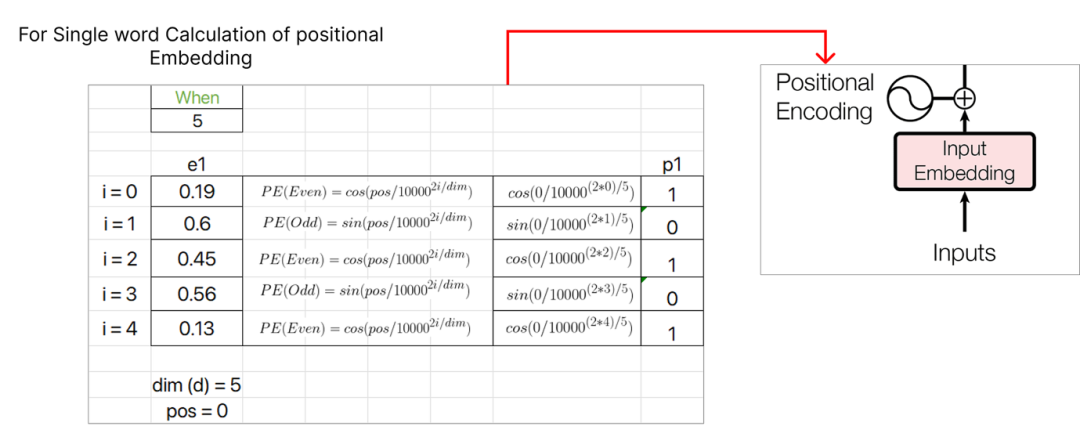
繼續計算位置embedding,我們將為下一個單詞“you” 分配pos值1,并繼續為序列中的每個后續單詞遞增pos值。 
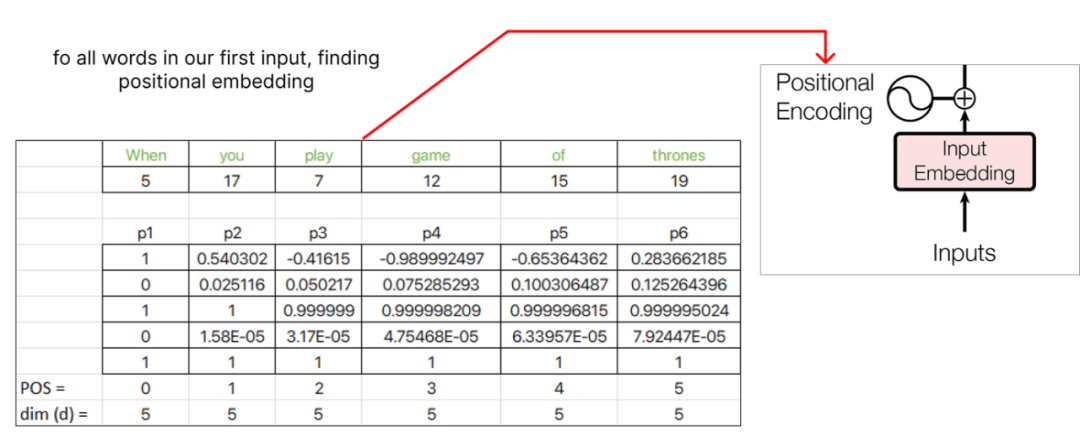
找到位置embedding后,我們可以將其與原始單詞embedding聯系起來。
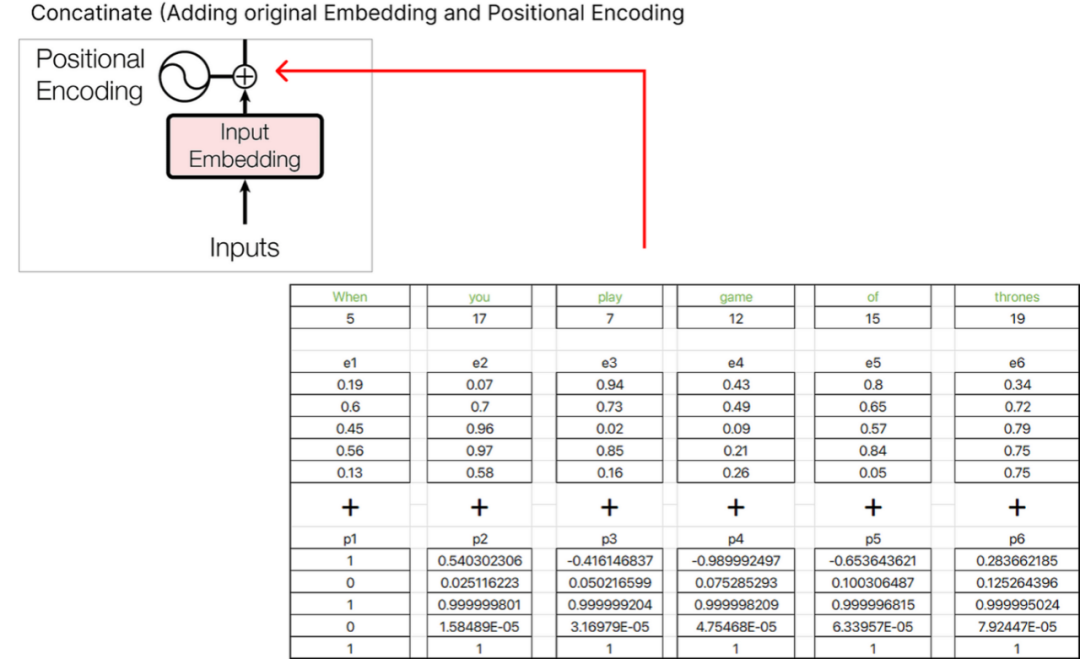
 我們得到的結果向量是e1+p1,e2+p2,e3+p3等諸如此類的embedding和。 ?
我們得到的結果向量是e1+p1,e2+p2,e3+p3等諸如此類的embedding和。 ?
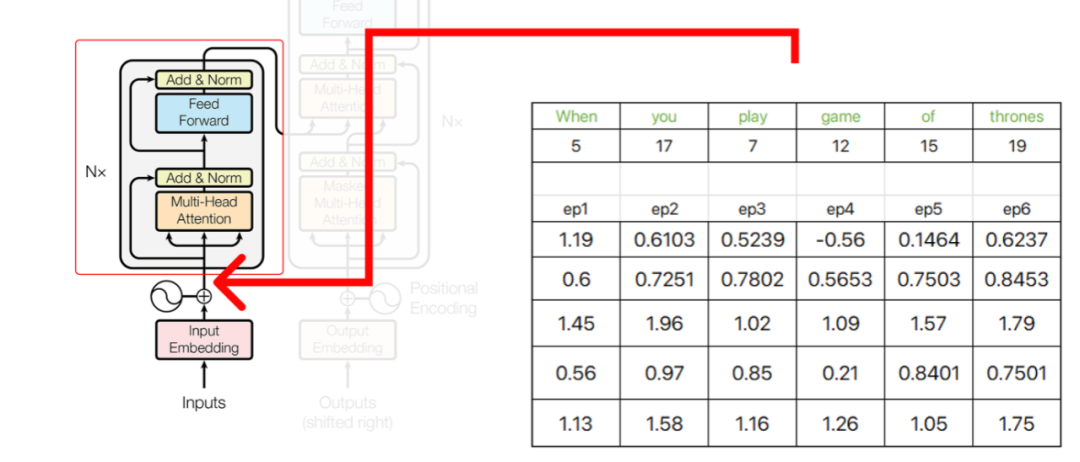
 Transformer架構的初始部分的輸出將在之后用作編碼器的輸入。 ?
Transformer架構的初始部分的輸出將在之后用作編碼器的輸入。 ?
在編碼器中,我們執行復雜的操作,涉及查詢(query),鍵(key)和值(value)的矩陣。這些操作對于轉換輸入數據和提取有意義的表示形式至關重要。 
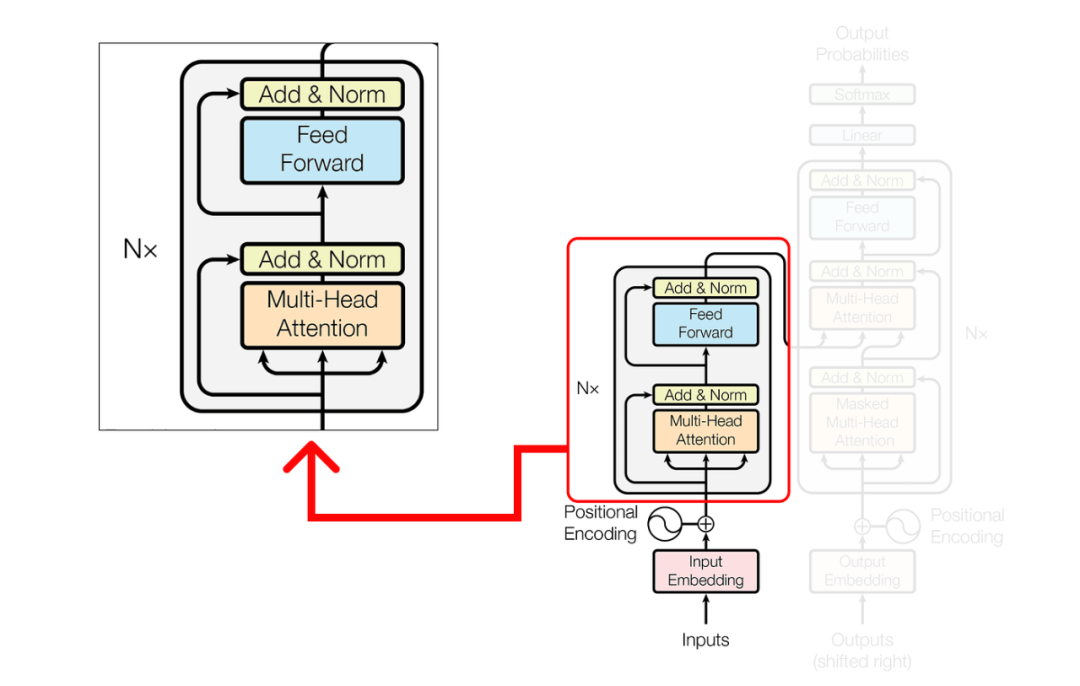
在多頭注意力(multi-head attention)機制內部,單個注意層由幾個關鍵組件組成。這些組件包括: 
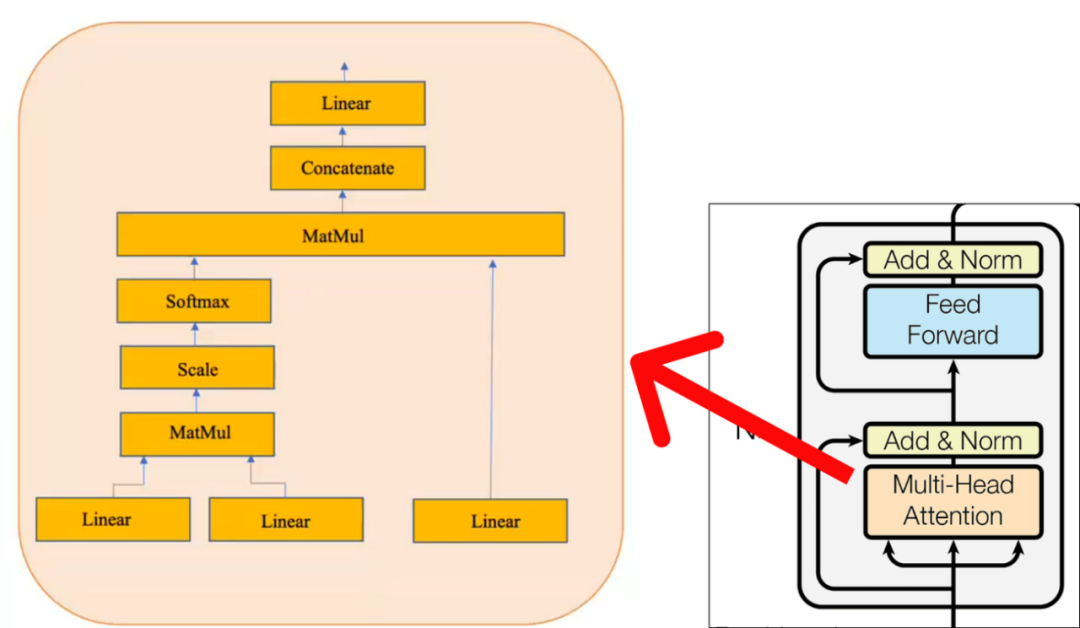
請注意,黃色框代表單頭注意力機制。讓它成為多頭注意力機制的是多個黃色盒子的疊加。出于示例的考慮,我們將僅考慮一個單頭注意力機制,如上圖所示。
Step 1 (Performing Single Head Attention)
注意力層有三個輸入
Query
Key
Value


在上面提供的圖中,三個輸入矩陣(粉紅色矩陣) 表示從將位置embedding添加到單詞embedding矩陣的上一步獲得的轉置輸出。另一方面,線性權重矩陣(黃色,藍色和紅色) 表示注意力機制中使用的權重。這些矩陣的列可以具有任意數量的維數,但是行數必須與用于乘法的輸入矩陣中的列數相同。在我們的例子中,我們將假設線性矩陣(黃色,藍色和紅色) 包含隨機權重。這些權重通常是隨機初始化的,然后在訓練過程中通過反向傳播和梯度下降等技術進行調整。所以讓我們計算(Query, Key and Value metrices): 
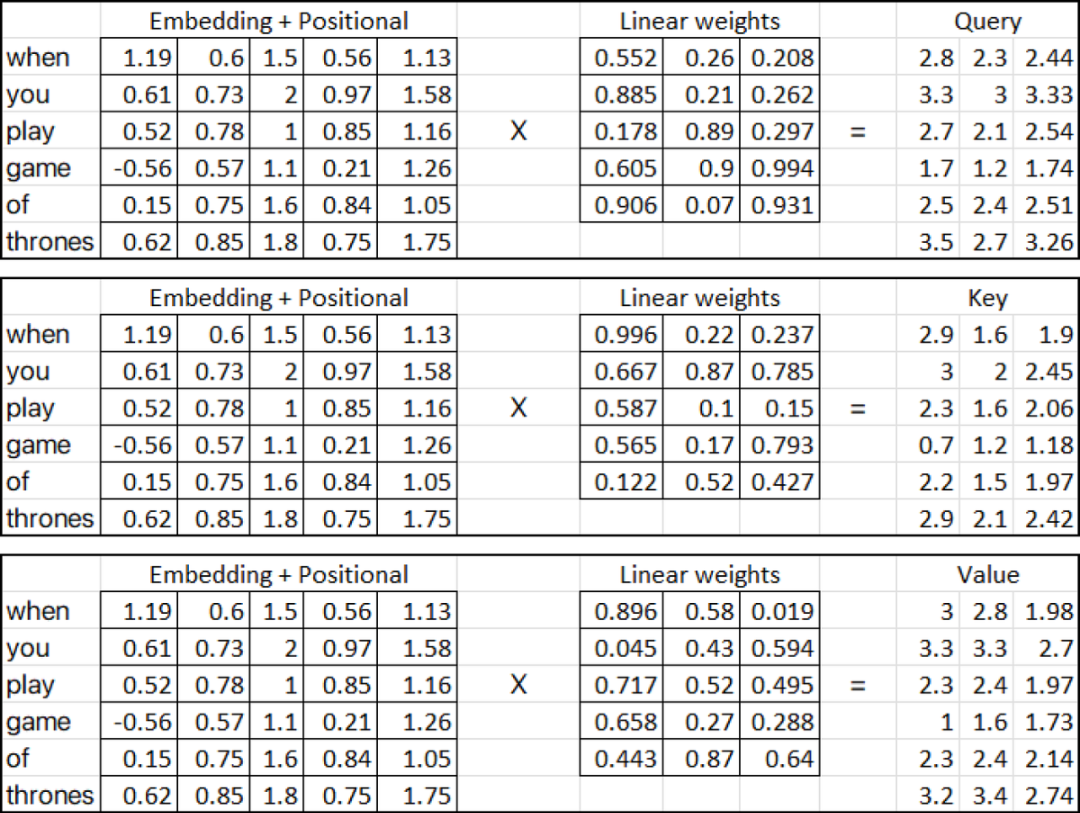
一旦我們在注意力機制中有了query, key, 和value矩陣,我們就繼續進行額外的矩陣乘法。 

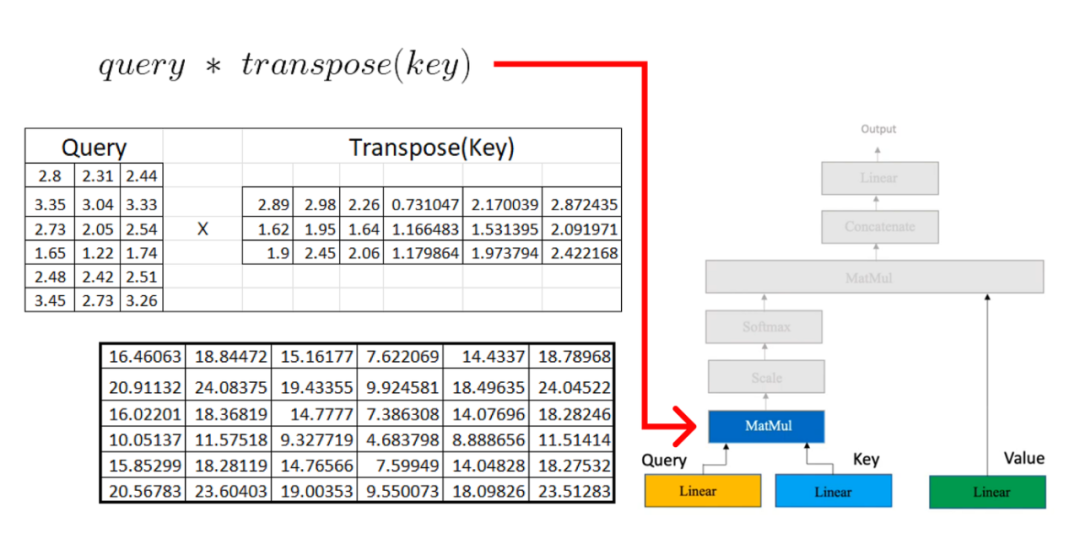
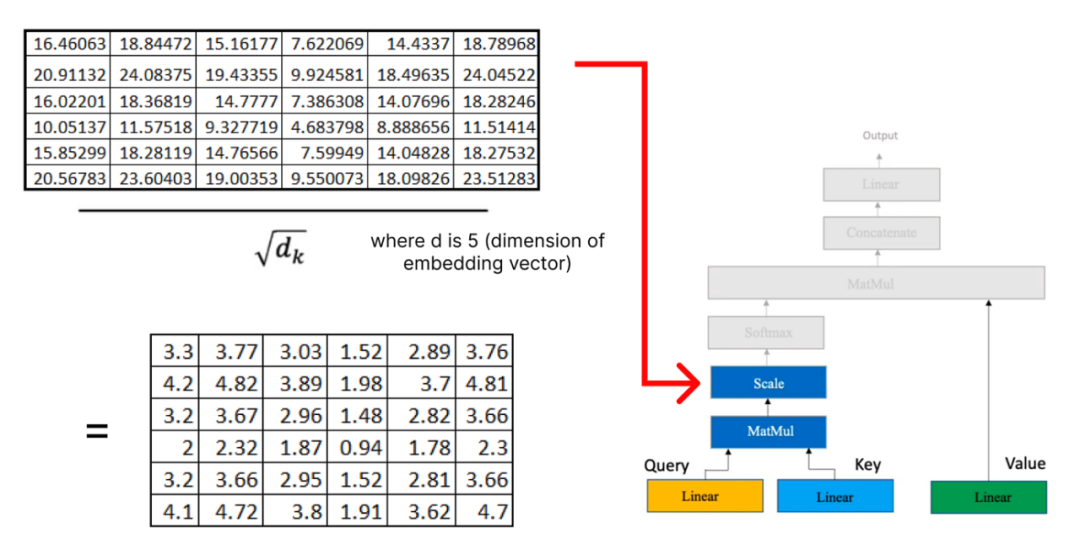

 現在,我們將結果矩陣與我們之前計算的值矩陣相乘:
現在,我們將結果矩陣與我們之前計算的值矩陣相乘: 
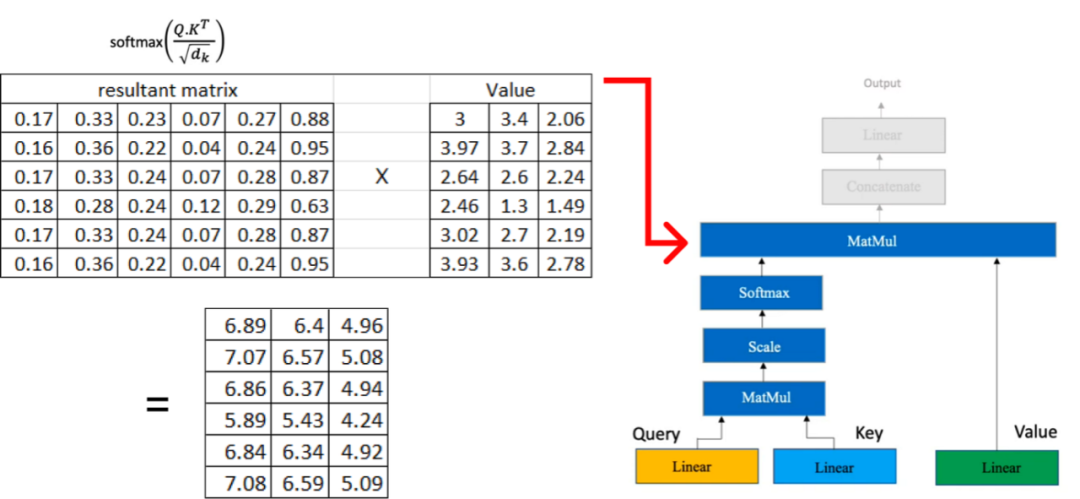
如果我們有多個頭部注意力,每個注意力都會產生一個維度為(6x3) 的矩陣,那么下一步就是將這些矩陣級聯在一起。 
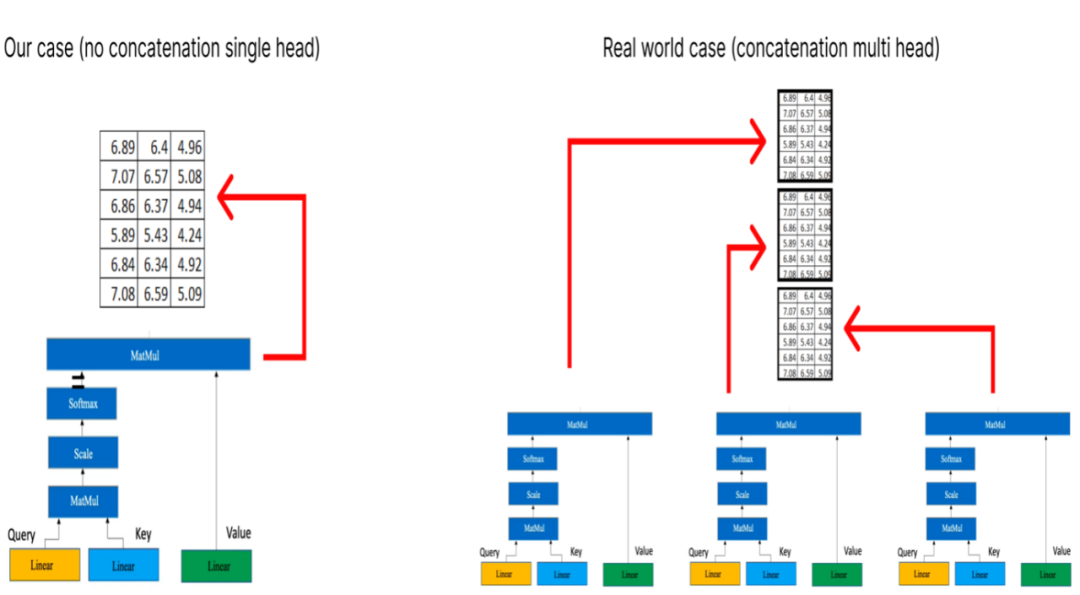
在下一步中,我們將再次執行類似于用于獲取query, key, 和value矩陣的過程的線性轉換。此線性變換應用于從多個頭部注意獲得的級聯矩陣。 
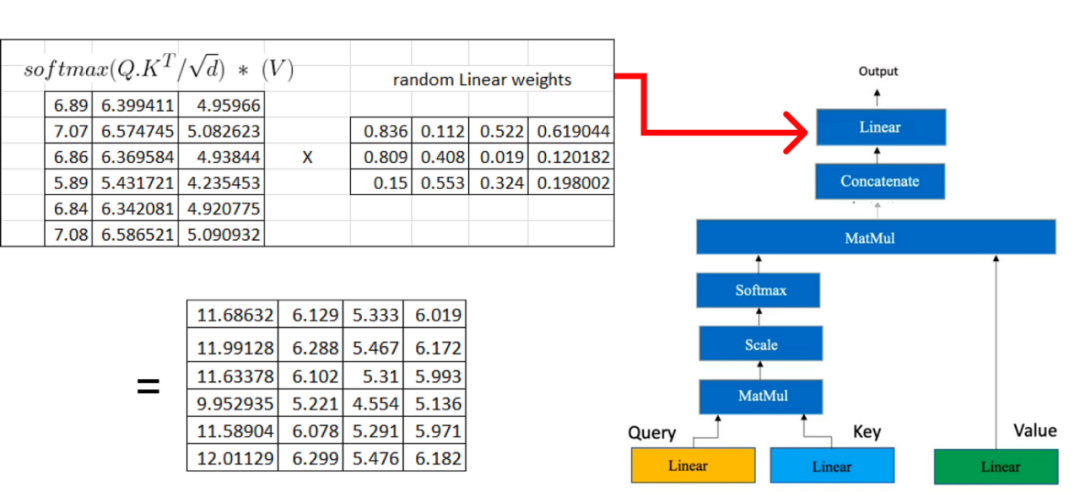
編輯:黃飛
-
函數
+關注
關注
3文章
4345瀏覽量
62937 -
Transformer
+關注
關注
0文章
145瀏覽量
6043
原文標題:圖解!逐步理解Transformers的數學原理
文章出處:【微信號:vision263com,微信公眾號:新機器視覺】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
手機通信原理解析
如何更改ABBYY PDF Transformer+界面語言
解析Transformer中的位置編碼 -- ICLR 2021

基于Transformer的目標檢測算法

BEV人工智能transformer
基于Transformer的目標檢測算法難點

大模型基礎Transformer結構的原理解析
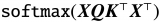
更深層的理解視覺Transformer, 對視覺Transformer的剖析




 transformer原理解析
transformer原理解析











評論