1電機電磁力的基本概念
電機運行時,其內部有三類電磁力存在,分別是麥克斯韋張力、洛倫茲力及磁致伸縮力。導致電機電磁振動的主要因素是鐵心受到的麥克斯韋張力,且定子受到的電磁力絕大部分作用于定子齒尖。為便于分析,一般將電磁力分解為徑向電磁力和切向電磁力,徑向電磁力比切向電磁力的分量大很多,徑向電磁力經齒傳遞到軛部,引起定子軛部徑向的形變。切向電磁力導致轉矩波動,引起齒部切向形變,將引起軸系共振。
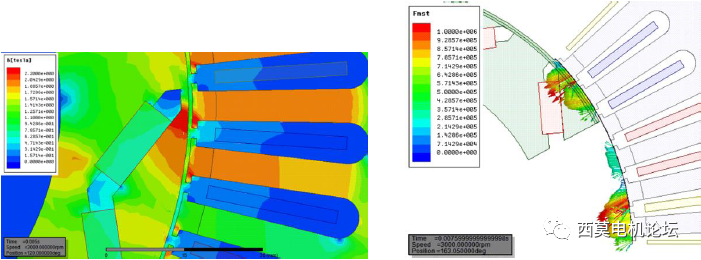
徑向電磁力
其中,Maxwell應力張量法表達式如下。
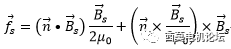
徑向電磁力及切向電磁力表達式如下,其單位均為N/m2。
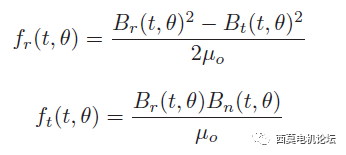
在Maxwell中,通過場計算器添加徑向電磁力Br及切向電磁力Bt可按如下操作進行。
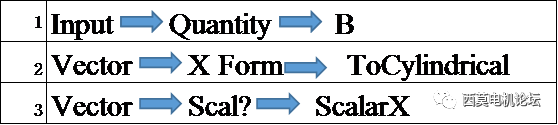
添加Br
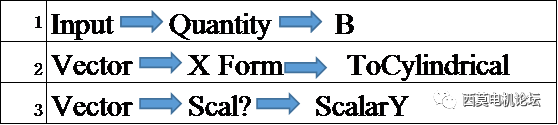
添加Bt
徑向及切向電磁力密度表達式如下。
徑向電磁力:(Br^2-Bt^2)/Mu0/2
切向電磁力:(Br*Bt)/Mu0
最終,在Maxwell中生成如下所示的徑向及切向電磁力表達式。
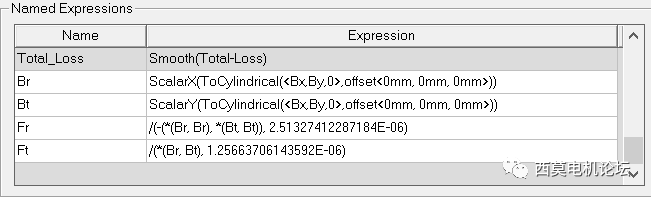
徑向及切向電磁力表達式
利用Maxwell瞬態場仿真得到定子齒部某點電磁力隨時間變化的結果,通常,時域下的電磁力難以獲得足夠的信息,因此,我們需要將電磁力從時域變換到頻域,即一維傅里葉變換。利用離散傅里葉變換(DFT),將隨時間變化的波形轉換到頻域,得到各次頻率諧波的幅值及相位,這種時域到頻域的轉換,便于對復雜電磁力波的分析與優化,并應用于結構諧響應分析。
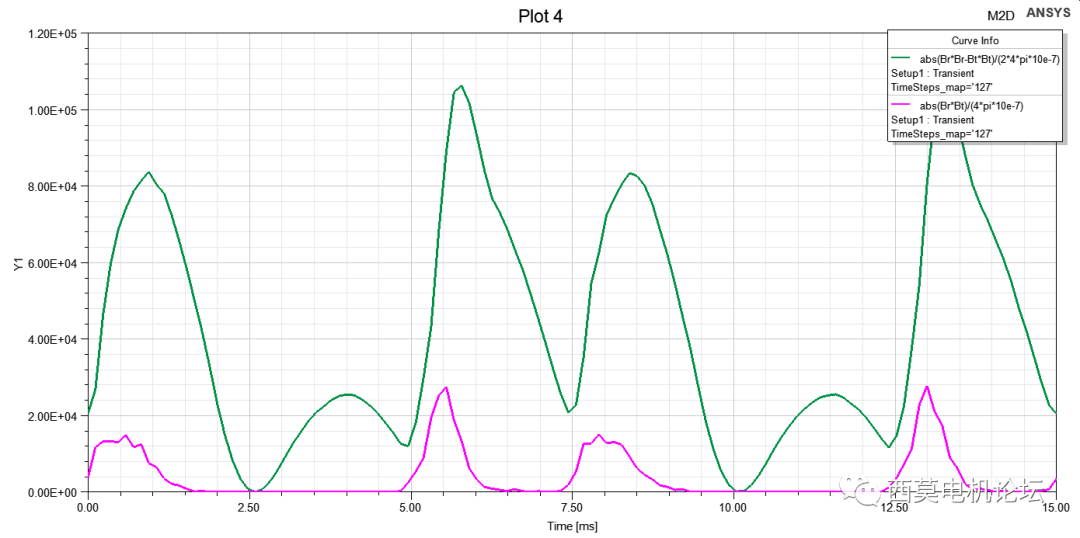
時域電磁力
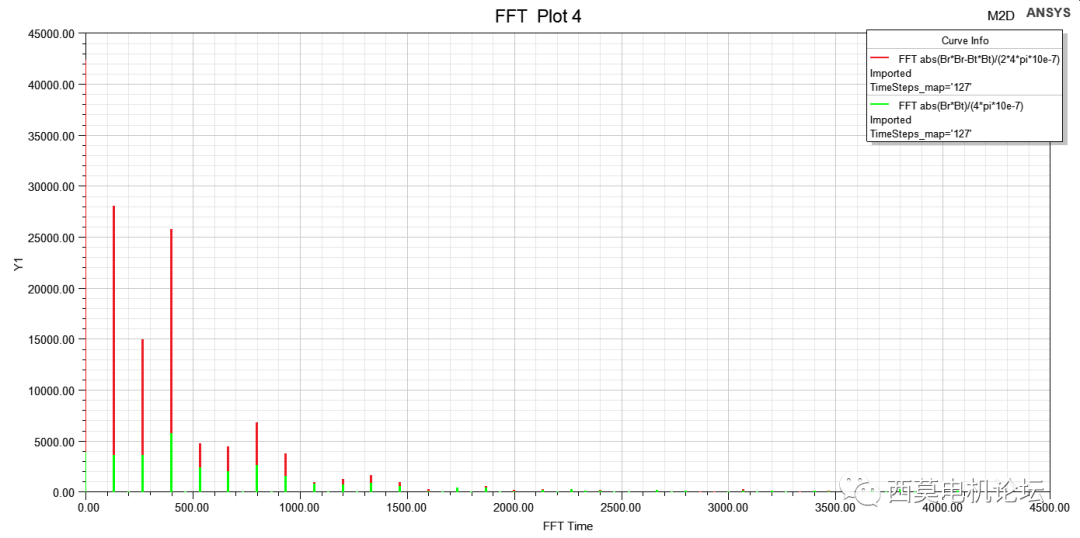
頻域電磁力
轉子旋轉運動時,從整個氣隙圓周上看,電磁力同時具有時間和空間屬性。電磁力在時域下看似雜亂無序,但從其產生根源分析,它可以看成由無數個具有不同幅值、空間階數、時間階數的旋轉運動的行波疊加而成。
徑向電磁力可分解為如下表達式。
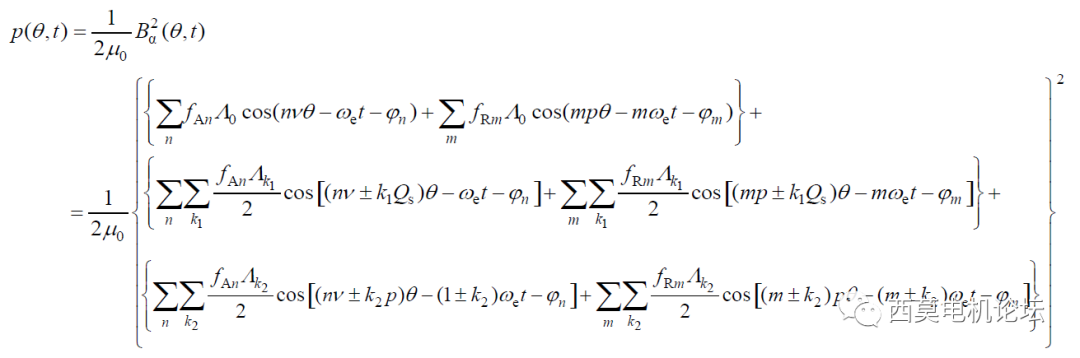
在這些無窮盡的諧波分量中,有一些分量對電機NVH有較大的影響。如空間階數 <= 4 且其幅值較大時,亦或是空間階數和(或)頻率(時間階數)與定子鐵心的固有振型及固有頻率接近或相等時,當這些情況發生時,電機將會產生較大的噪音,影響電機聲品質結果。
因此,如果我們可以提取出這些關鍵的時、空電磁力諧波分量,并將其作為優化目標,那么電機NVH的優化流程無需進行結構諧響應分析,優化設計效率將大幅提高。因此,我們可以通過二維傅里葉變換(Two-Dimensional FourierTransform(2DFFT))來對這些諧波含量進行提取,然后有針對性的對其進行優化降低。

二維傅里葉變換(Two-Dimensional Fourier Transform(2DFFT))
在2022R2版本之前,Maxwell無法直接進行FFT2D,因此我們開發了用于FFT2D的UDO腳本,可實現用戶指定的任意時、空階次幅值的輸出,同時支持導出所有FFT2D結果矩陣到csv文件,利用該腳本即可實現對電磁力某時、空階次幅值的優化。
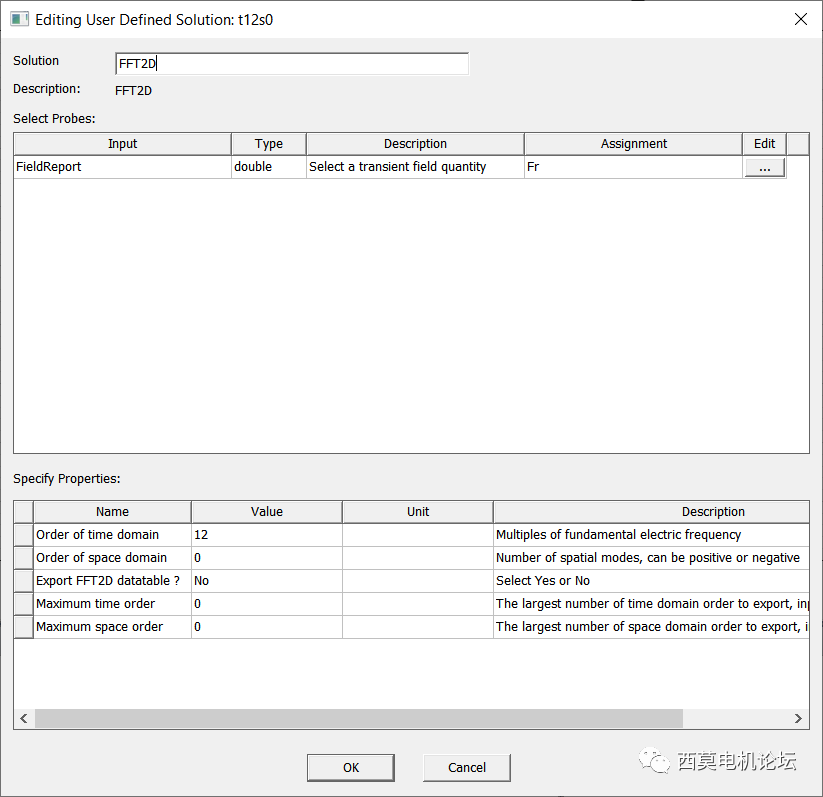
FFT2D腳本
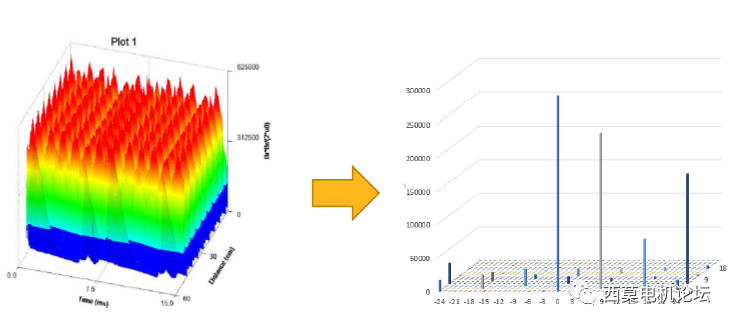
導出所有FFT2D結果矩陣到csv文件并圖標顯示結果
Maxwell 2022R2新增電磁力二維傅里葉變換功能,用戶可直接在軟件中進行電磁力二維傅里葉變換,無需借助腳本。
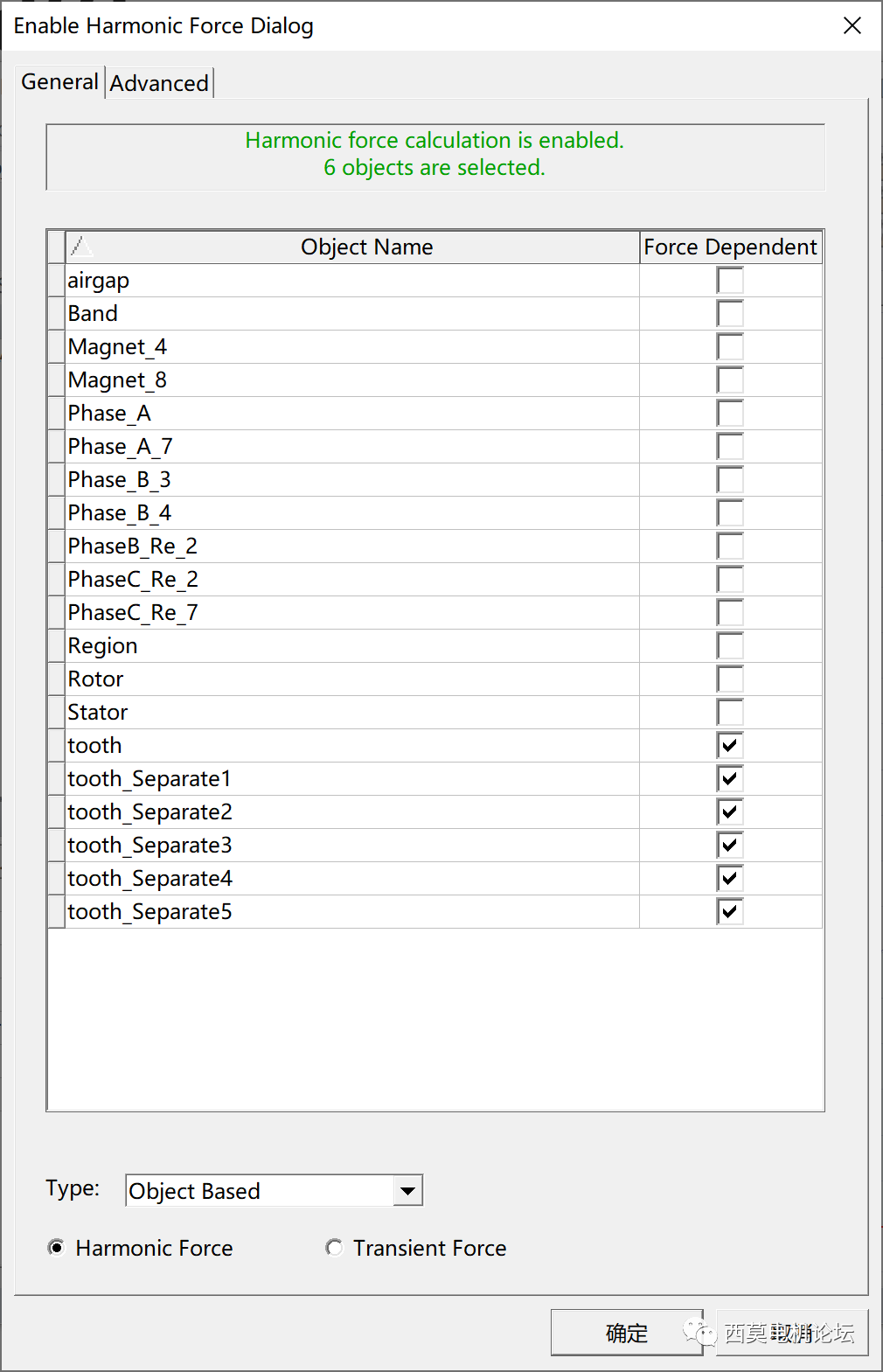
首先進行object Based諧波電磁力計算
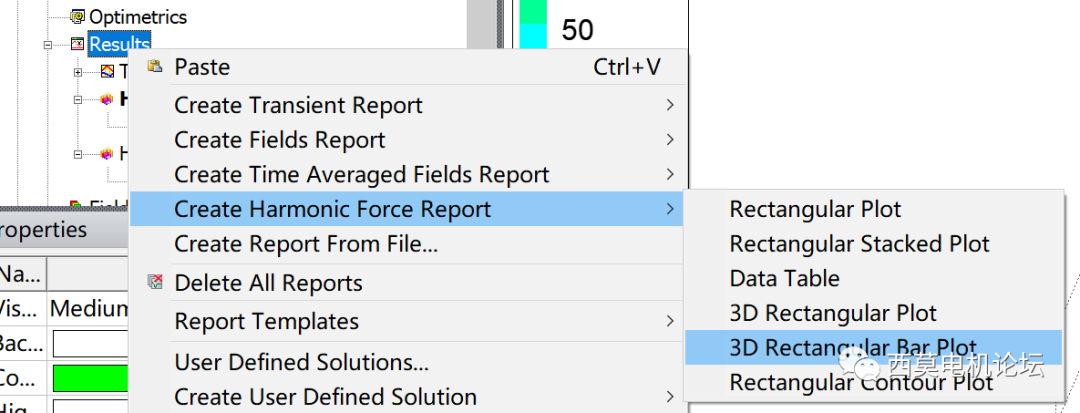
Maxwell 2022R2新增電磁力二維傅里葉變換
軟件新增諧波電磁力的3D柱狀圖顯示功能。
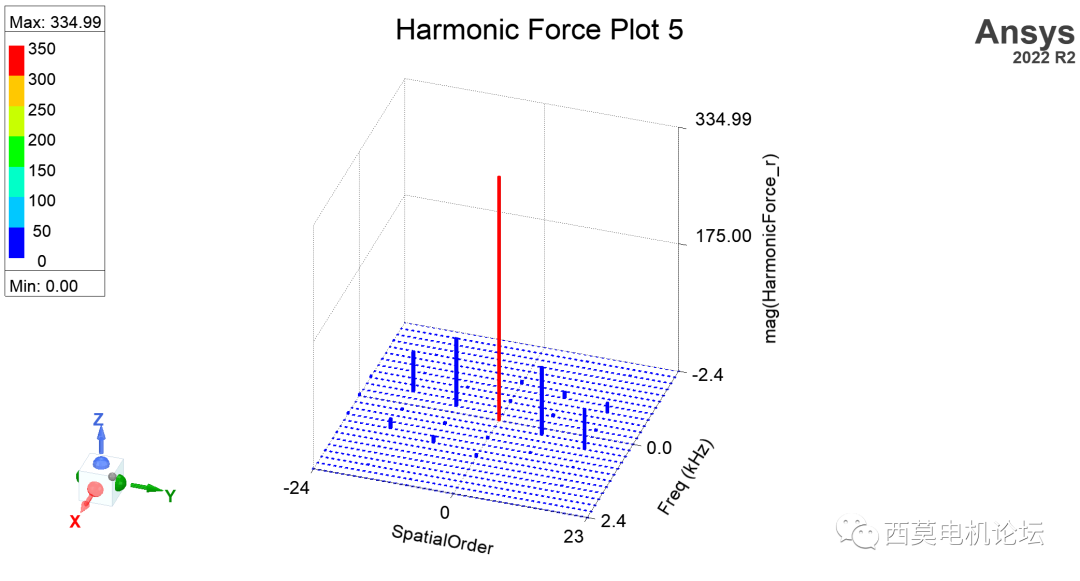
諧波電磁力的3D柱狀圖顯示
關于諧波電磁力的2D結果如下圖所示。
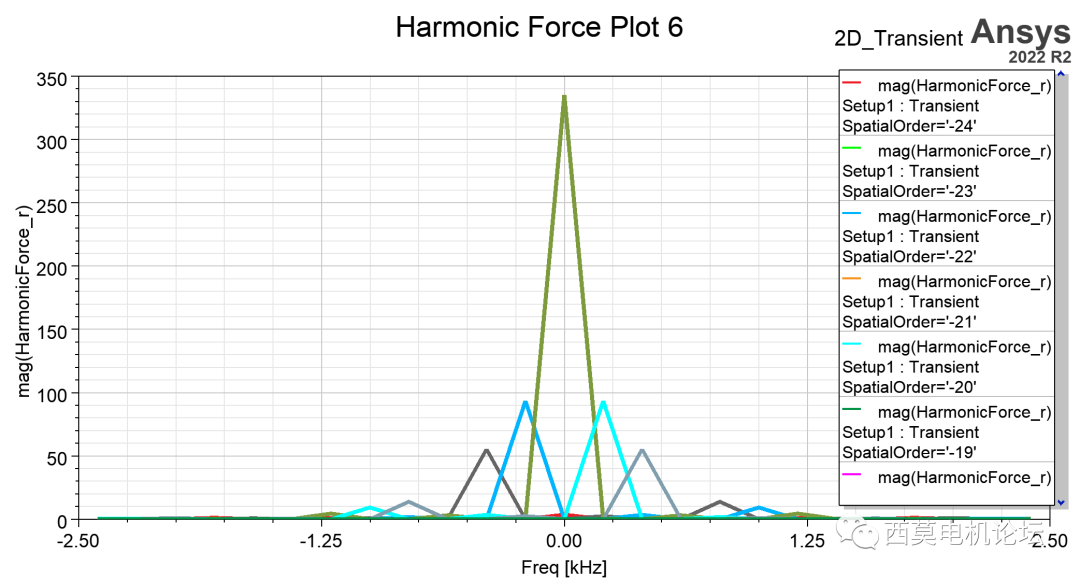
諧波電磁力的2D結果
諧波電磁力結果基于二維離散傅里葉變換,坐標顯示為空間階數和時間頻率階數,支持Mag, Re, Imag, Phase選項,軟件基于object based諧波電磁力計算結果進行后處理,因此不需要保存場數據。
新增電磁力二維傅里葉變換功能可以識別引起震動的主要空間和時間階次電磁力,同時支持電磁力插值(by Inverse DFT)。
2電機時空二維電磁力諧波的優化設計
接下來將以一V字內置式永磁電機為例,闡述如何利用FFT2D UDO腳本和Ansys optiSLang,對典型的V字內置式永磁電機的電磁力等參數進行敏感性分析與優化。本案例同時展示了如何實現Ansys optiSLang直接調用Maxwell進行優化設計的方法
電機原始設計方案如下。
電機拓撲結構為8極48槽、V字磁鋼、轉子表面輔助槽。
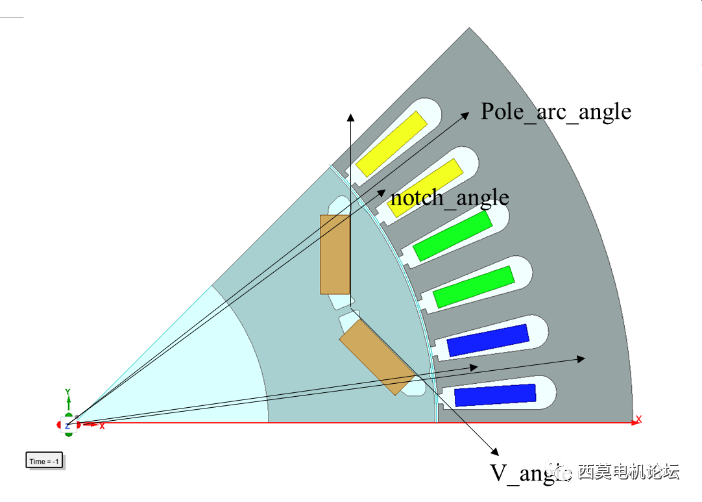
使用 V_Shape_IPM_Rotor UDP 創建轉子參數化模型
此處我們選擇三個關鍵轉子參數作為設計變量,分別為:
(1) 轉子輔助槽圓心角Notch_Angle=120deg;
(2)磁鋼V夾角V_Angle=135deg;
(3)極弧角度Pole_Arc_Angle=120deg。
原始方案計算的結果如下。
(1) 平均轉矩Torque_avg=189.8Nm
(2) 轉矩波動Torque_ripple=21.5%
(3) 磁鋼總面積PM_area=97.9mm^2
(4) 電磁力階次幅值
(a) 時間12階空間0階電磁力Force_t12s0=11246.2
(b) 時間6階空間0階電磁力Force_t6s0=10462.8
(c) 時間14階空間8階電磁力Force_t14s8=7759.8
用戶需在Maxwell中創建輸出報告,optiSLang會自動提取報告中的數據。
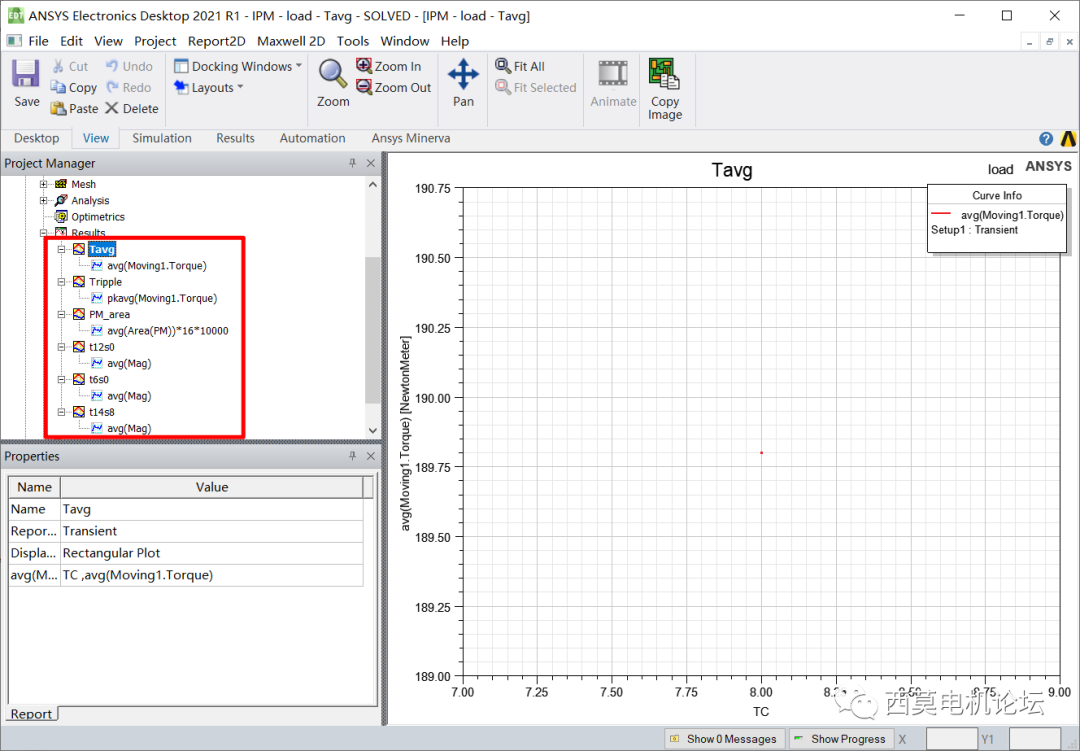
Maxwell中創建輸出報告
用戶需Maxwell中進行額外設置。默認設置下,每次輸出報告刷新后,UDO腳本都會執行一次,當UDO中有大量計算時,這將浪費很多時間。實際上只需最后一個時間步計算結束后執行一次FFT2D,因此我們做如下設置,該設置使Maxwell的報告僅在仿真結束后進行刷新。
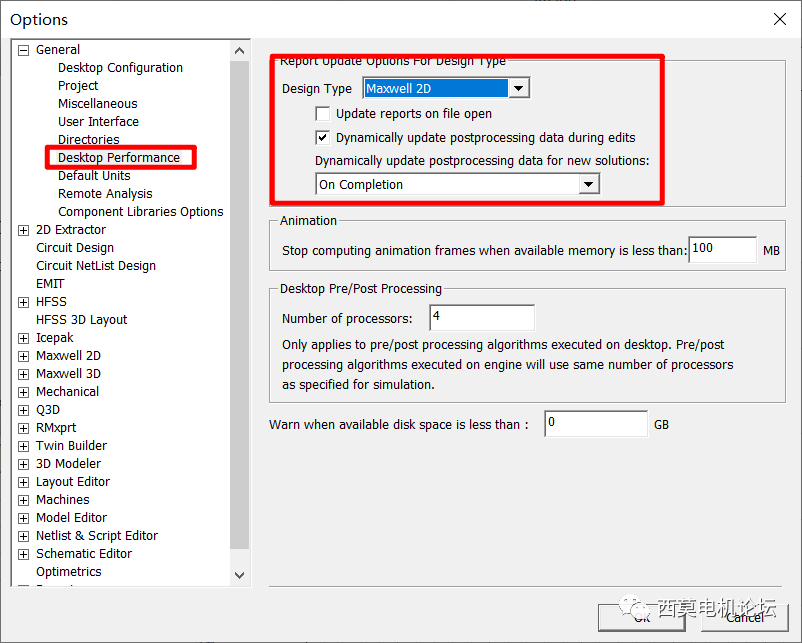
Maxwell中額外設置
接下來進行optiSLang的設置。
首先使用 導入Maxwell模型①。
導入Maxwell模型①。
導入Maxwell模型
然后打開AEDT節點設置②,然后設置ansysaedt.exe路徑③,然后使用RegularDSO模式④,然后勾選保存場和網格⑤,選擇自動刪除AEDT結果文件(可選)⑥,最后保存設置即可⑦。
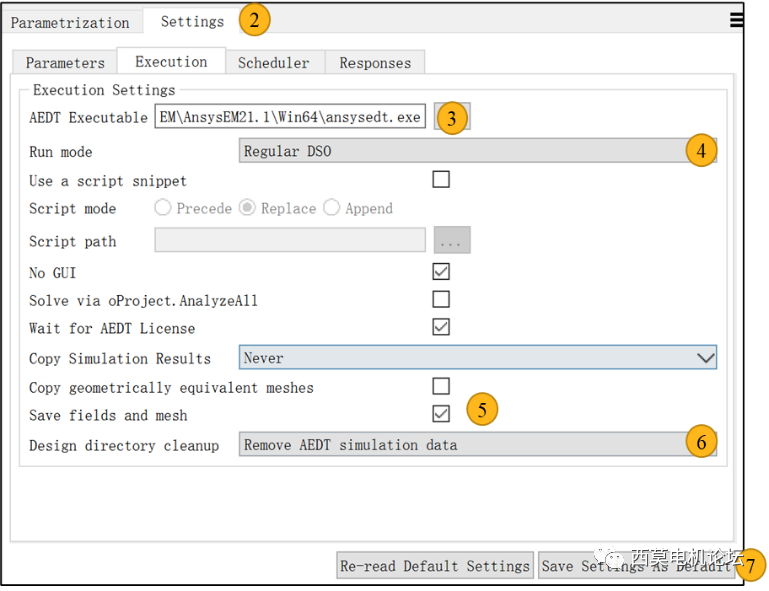
optiSLang設置
接下來設置Parameter參數①,然后設置Response參數②、設置AEDT每次并行求解的設計方案數③、最后設置最大的AEDT求解器并行數④。
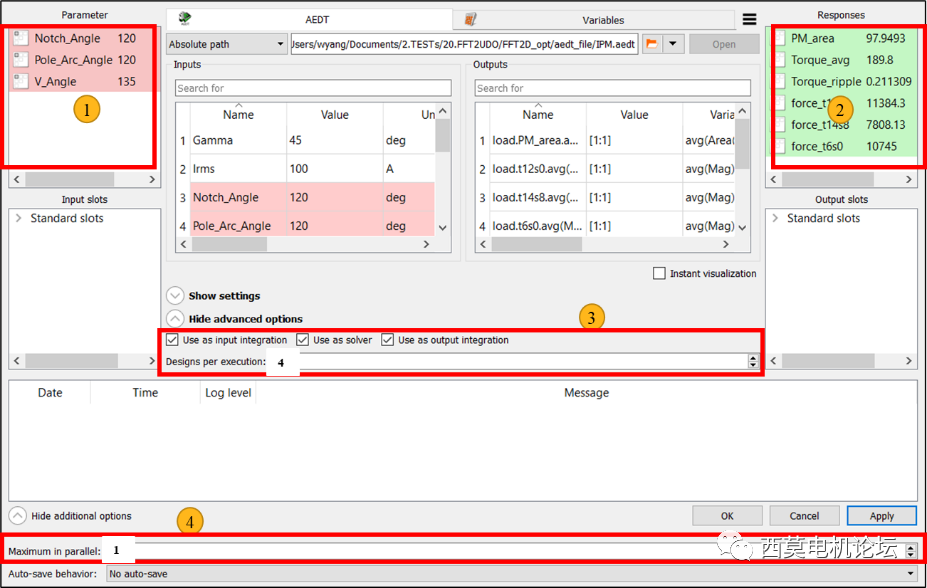
optiSLang設置
接下來進行optiSLang敏感度分析。
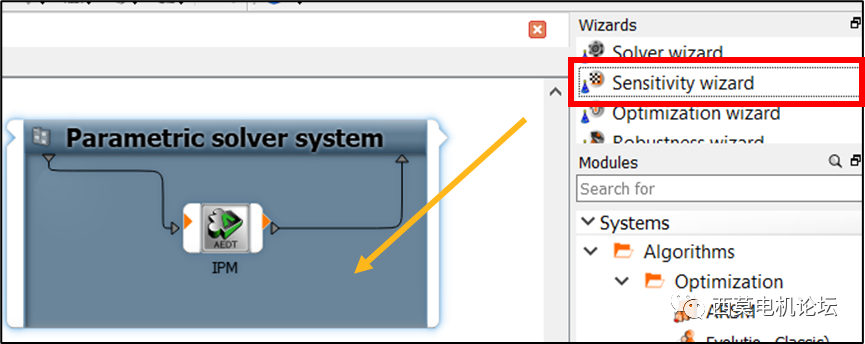
optiSLang敏感度分析
然后定義變量范圍。
(1) 轉子輔助槽圓心角Notch_Angle:90deg~140deg
(2) 磁鋼V夾角V_Angle:100deg~170deg
(3) 極弧角度Pole_Arc_Angle:100deg~140deg

定義變量范圍
接下來設置采樣規則,此處我們使用默認的 Adaptive Metamodel of Optimal Prognosis(AMOP)采樣算法。
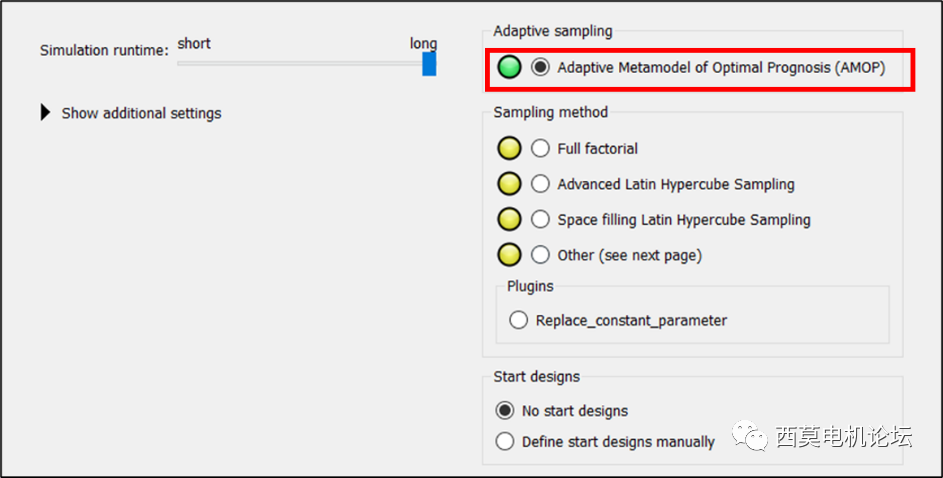
使用默認的 Adaptive Metamodel of OptimalPrognosis(AMOP)采樣算法
為了獲得高質量MOP模型,需要進行兩次AMOP,分別為AMOP Global和AMOP Local兩次。AMOP Global為大范圍DOE;AMOP Local為局部加密DOE采樣,其Local采樣基于Glob采樣結果。
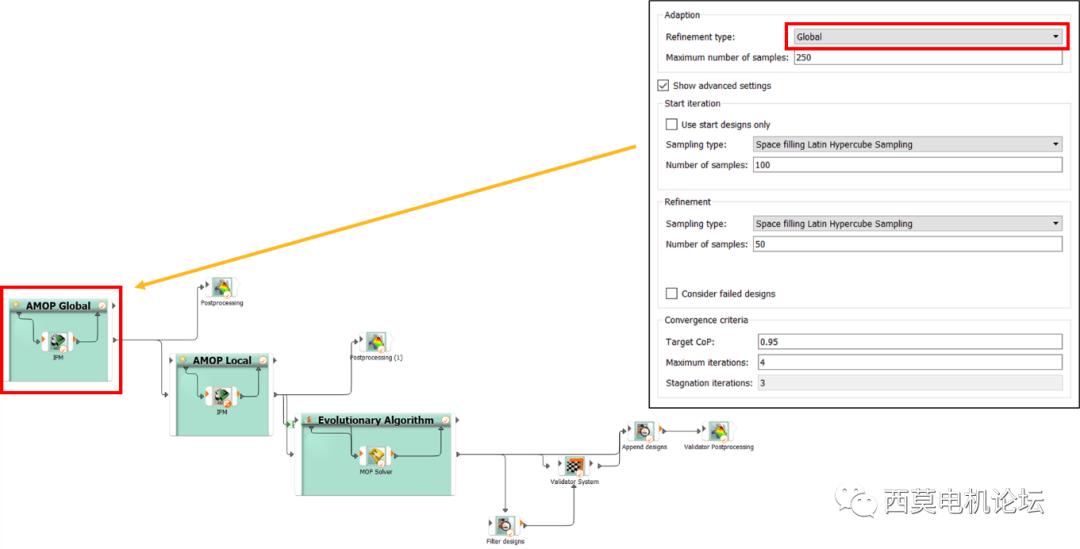
AMOP Global
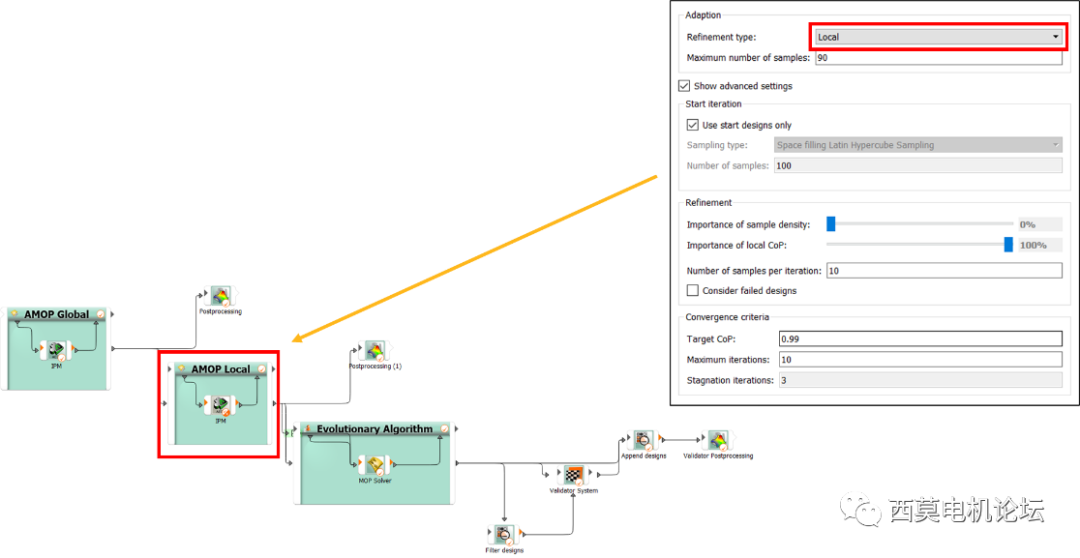
AMOP Local
接下來查看optiSLang敏感度分析結果,經過兩次AMOP后,Maxwell共計算340個design,所有響應值都獲得了較高精度的MOP模型。AMOP Global及AMOP Local模型分別如下圖所示。
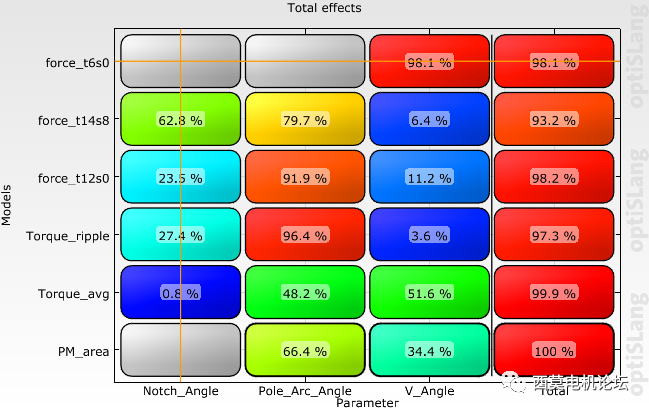
AMOP Global模型
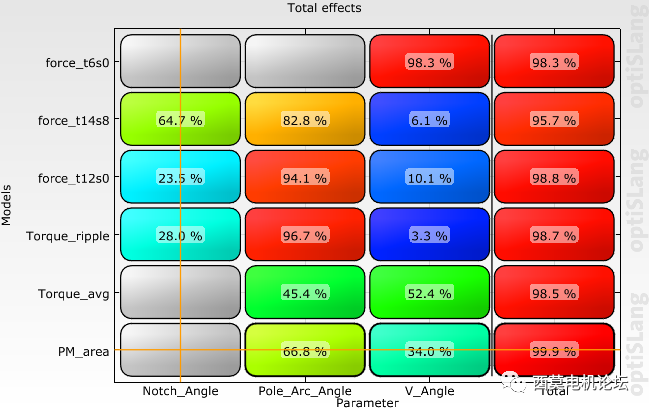
AMOP Local模型
接下來查看參數相關性矩陣,參數相關性矩陣代表輸入參數對每個響應值的影響程度,也可以表達不同響應值之間的關系。
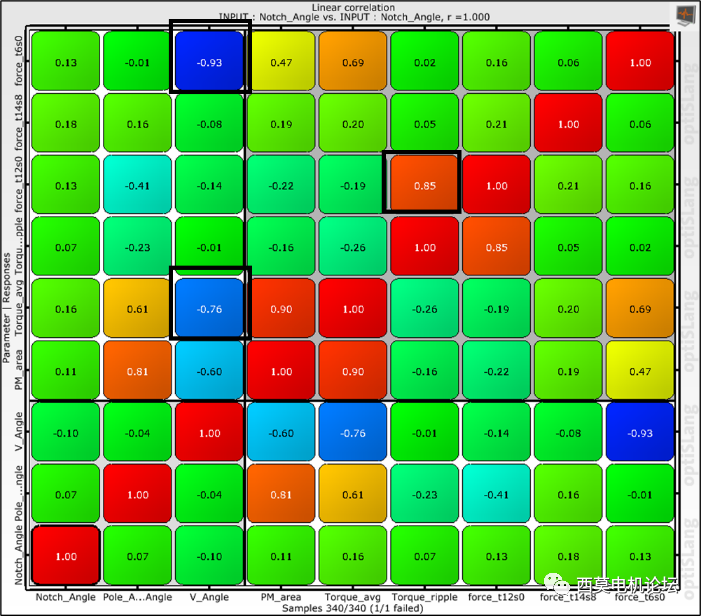
參數相關性矩陣
從參數相關性矩陣結果可看出,V_Angle與force_t6s0、Torque_avg有很強負相關性,且Force_t12s0與Torque_ripple有很強的正相關性。
接下來進行optiSLang優化。優化策略是在平均轉矩不變、成本不大幅增加的情況下,盡可能降低振動噪聲。因此我們定義優化目標
(1) Torque_avg>=190Nm
(2) Torque_ripple最小化
(3) 各階次電磁力幅值最小化
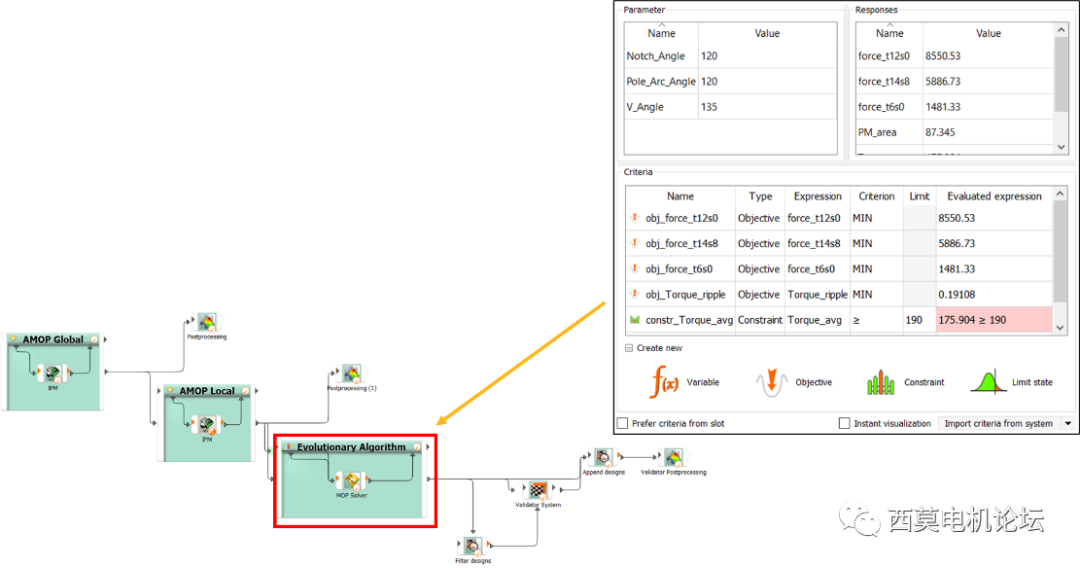
optiSLang優化
接下來選擇EvolutionaryAlgorithm優化算法。選擇后將會自動添加Validator System。
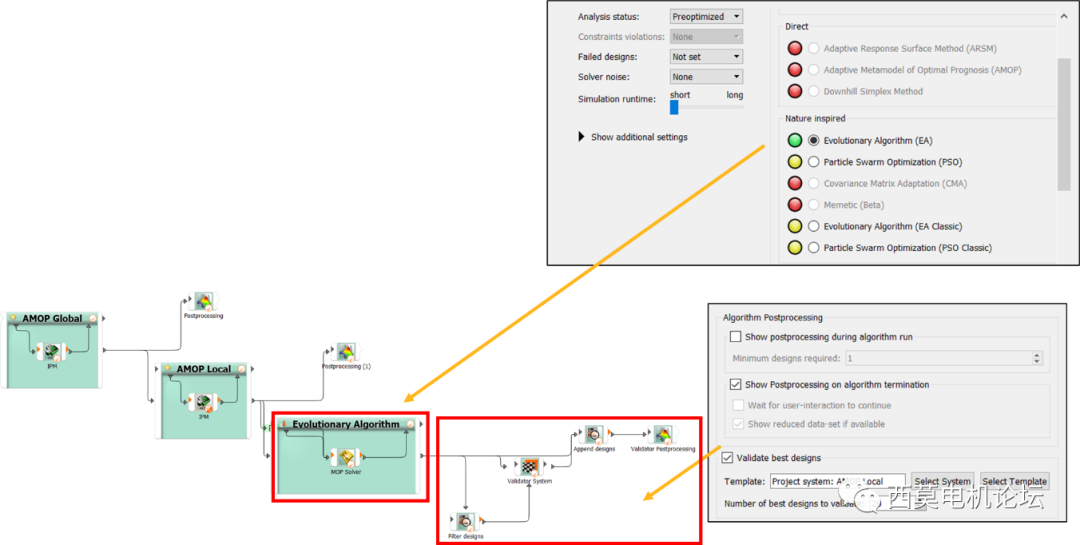
選擇Evolutionary Algorithm優化算法
最后,基于MOP模型的優化,10分鐘計算了10000個design,其中有8162個design滿足約束條件。
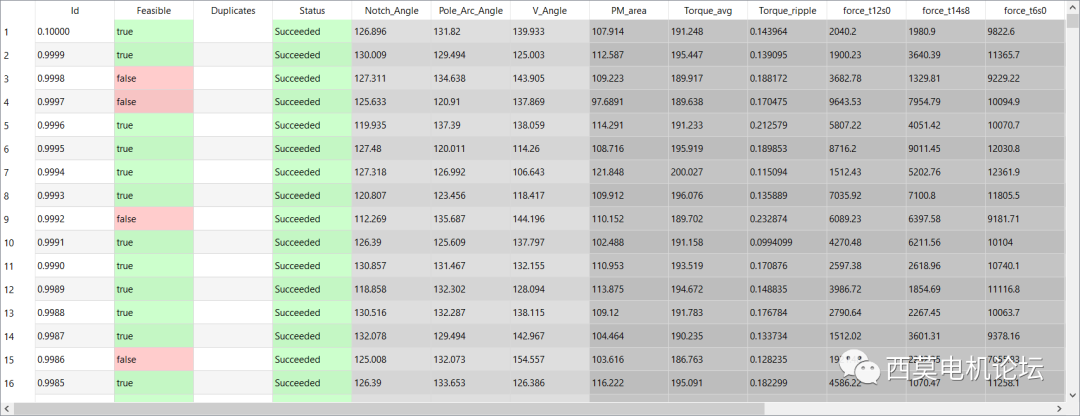
計算結果
通過查看2D帕累托前沿結果,可以發現某些響應值之間出現了較明顯的“蹺蹺板”現象,如下圖所示。
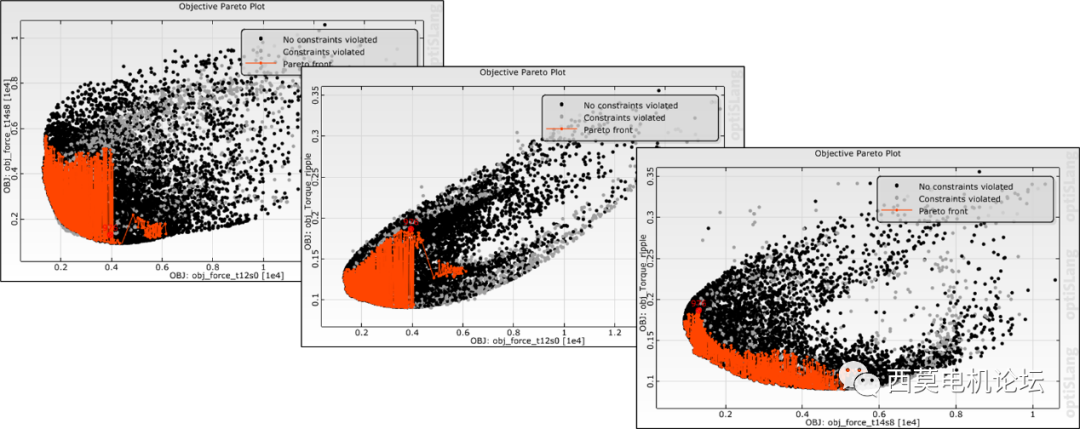
2D帕累托前沿
通過查看3D帕累托前沿結果,可知三個響應(Force_t12s0、Force_t14s8、Torque_ripple)之間形成了明顯的帕累托前沿。如下圖所示。
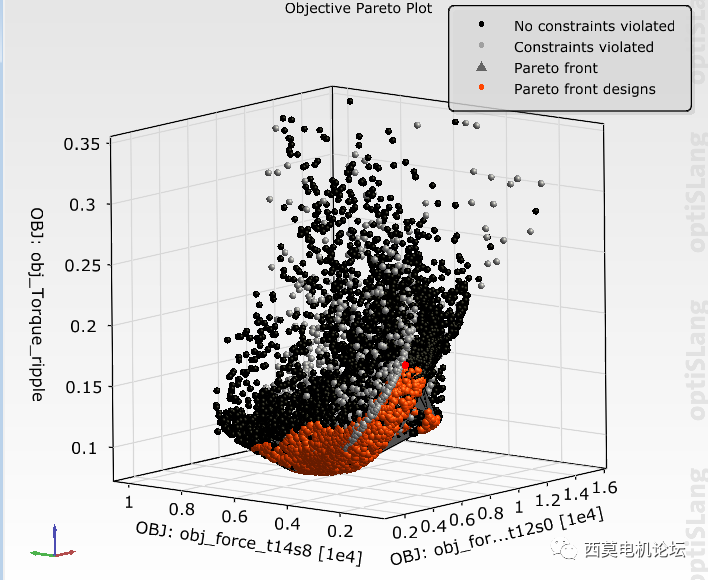
3D帕累托前沿
用戶可將MOP計算結果與Maxwell直接計算結果對比。
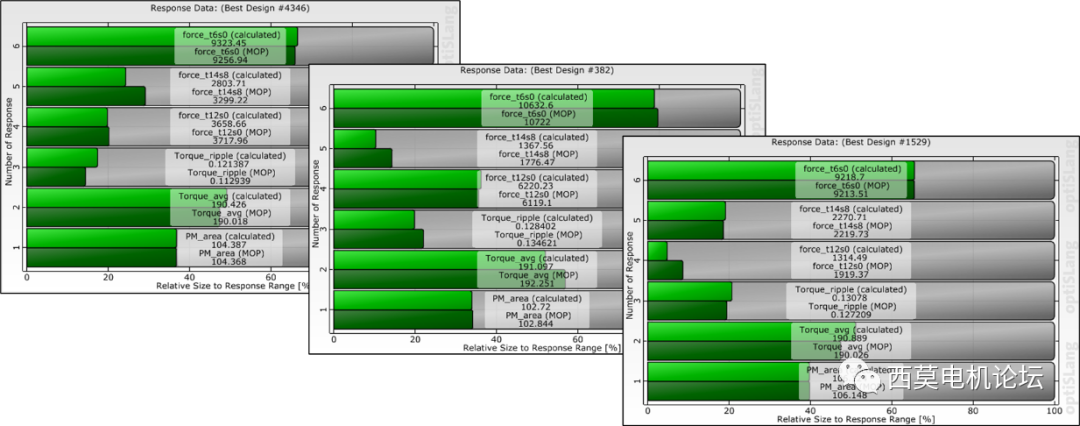
MOP計算結果
用戶可使用后處理工具Parallelcoordinates plot分析帕累托前沿解。每一列代表一個輸入或者響應值,每條曲線代表一個設計方案。
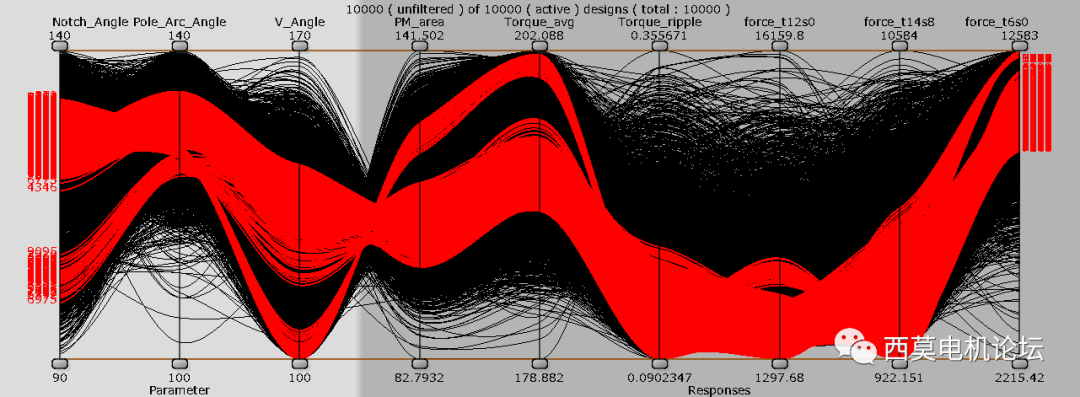
帕累托前沿解
本案例中有1351個帕累托解,用戶可使用后處理工具Parallel coordinates plot篩選設計方案,通過拖拽手柄快速縮小解集。
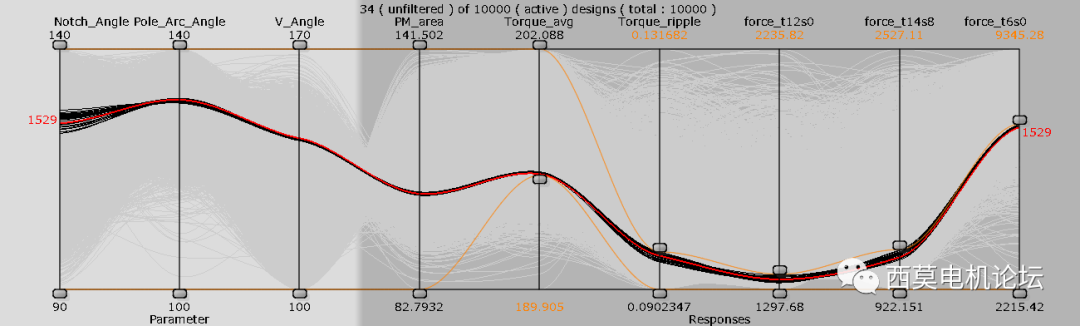
使用后處理工具Parallel coordinates plot篩選設計方案
本案例選擇帕累托前沿上的1529號方案作為優化方案。其參數變量取值及目標結果如下圖所示。
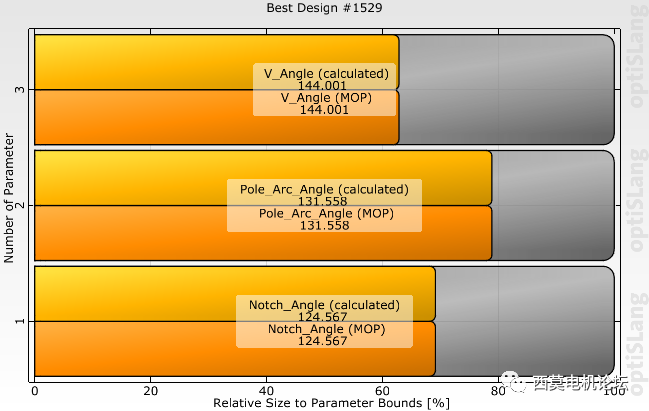
1529號方案變量取值
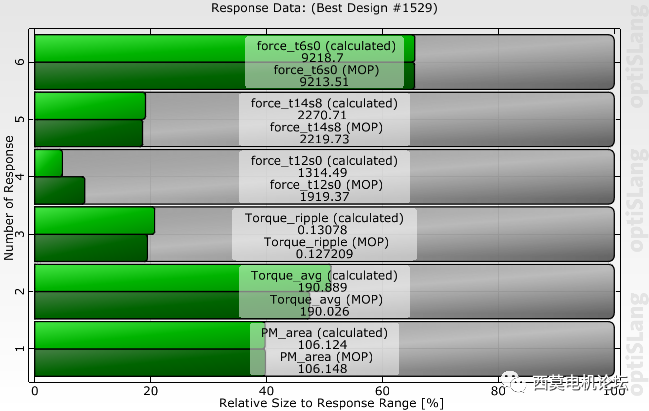
1529號方案目標結果
優化前后對比結果如下表所示。
優化前后對比結果對比表
| 參數 | 優化前 | 優化后 | 對比 |
| Notch_Angle | 120deg | 124.57deg | — |
| V_Angle | 135deg | 144deg | — |
| Pole_Arc_Angle | 120deg | 131.56deg | — |
| Force_t12s0 | 11246.2 | 1314.49 | -88.3% |
| Force_t6s0 | 10462.8 | 9218.7 | -11.9% |
| Force_t14s8 | 7759.8 | 2270.71 | -70.7% |
| Torque_avg | 189.8Nm | 190.9Nm | — |
| Torque_ripple | 21.5% | 13.1% | -39.1% |
| PM_area | 97.9mm^2 | 106.124mm^2 | +8.4% |
優化前后轉子結構模型如下圖所示。
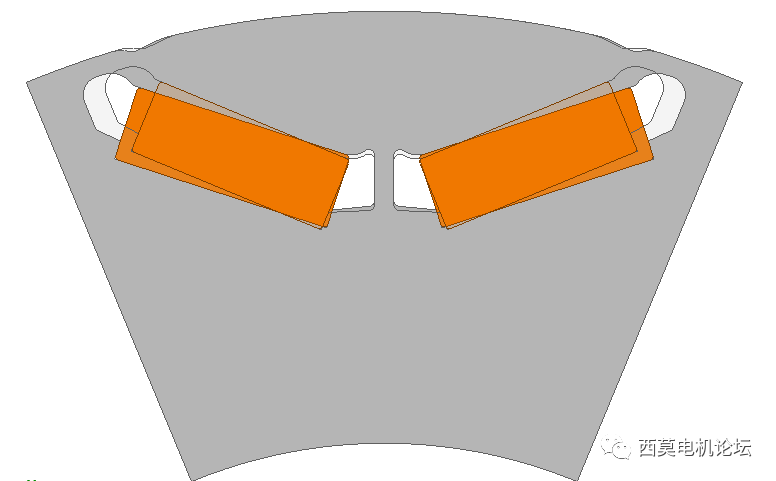
優化前后轉子結構模型
優化前后轉矩脈動對比如下圖所示,紅色為優化后方案,綠色為原始方案。
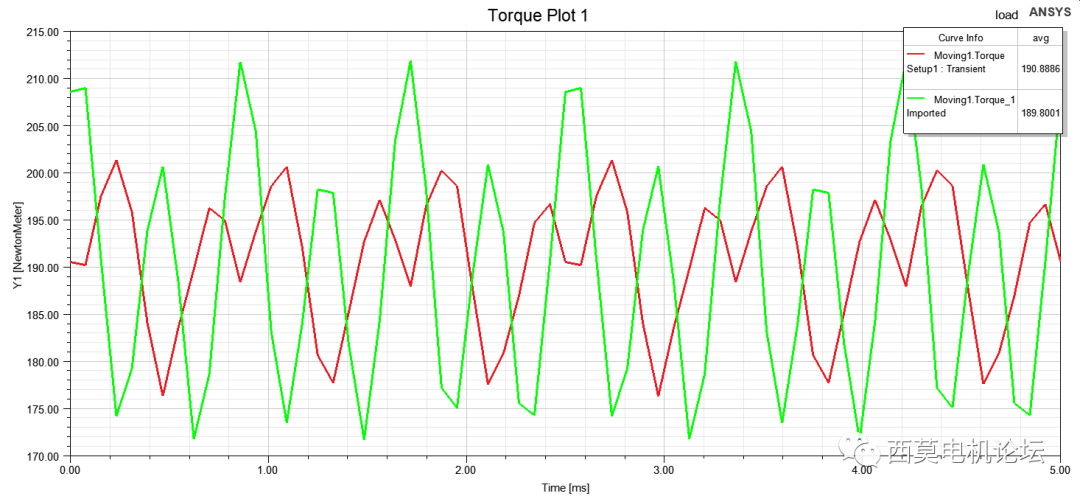
優化前后轉矩脈動對比
用戶可使用AnsysSound進行階次分析,分析結果如下圖所示。
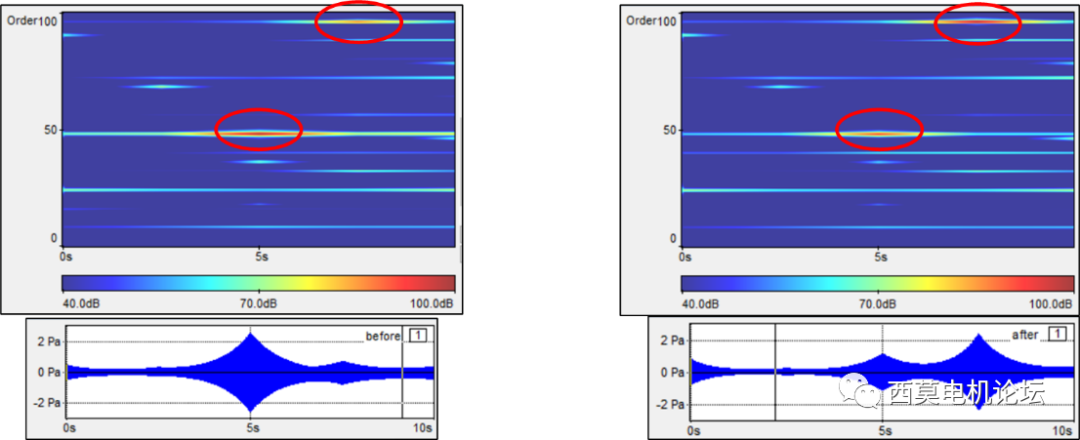
優化前 優化后
從上述結果可知,48階(force_t12s0)分貝減小,3750rpm@300Hz處由98.89dB下降到91.55dB。而96階(force_t24s0)分貝增大(未做優化),4875rpm@7800Hz處由86.42dB增加到97.71dB。
用戶也可通過AnsysSound生成電機噪音仿真結果,更加直觀的對聲品質進行評價。
3總結
Maxwell&optiSLang可高效的實現電機時空階次電磁力優化。用戶可利用UDP繪制非常復雜參數化幾何模型,利用UDO進行非常復雜的FEA結果后處理;同時optiSLang強大的優化后處理功能可以幫助用戶快速完成方案篩選與驗證。
電機階次電磁力被降階(MOP)的難度沒有想象中那么大,且階次電磁力會出現“此消彼長”的現象,因此用戶在進行NVH優化時,應首先進行定子諧響應分析,鎖定所有可能引起較大振幅的空間低階次電磁力分量,然后將它們全部設置為優化目標或約束條件,以此為目標優化后篩選出的方案將會更加合適。
審核編輯:劉清
-
變換器
+關注
關注
17文章
2109瀏覽量
109470 -
計算器
+關注
關注
16文章
437瀏覽量
37439 -
電磁力
+關注
關注
1文章
78瀏覽量
14289 -
傅里葉變換
+關注
關注
6文章
442瀏覽量
42672
原文標題:Ansys Maxwell&optiSLang電機時空二維電磁力諧波優化設計
文章出處:【微信號:西莫電機論壇,微信公眾號:西莫電機論壇】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
基于Ansys Workbench的Maxwell&;amp;optiSLang永磁電機聯設計
LabVIEW中怎樣將一維數組轉換成二維數組
Ansys Maxwell 3D 2D RMxprt v16.0 Win32-U\
大神們有了解Ansys Maxwell與Ansoft Maxwell這兩個軟件的嗎?
電磁仿真軟件哪里免費下載
HFSS二維薄片邊界設置應用技巧
永磁同步驅動電機徑向電磁力致噪聲的來龍去脈
使用VIRTUALLAB FUSION和ANSYS OPTISLANG進行跨平臺光學建模和設計
基于時空二維混沌的數字水印算法
歐拉 Summit 2021 安全&amp;可靠性&amp;運維專場:主流備份技術探討





 Ansys Maxwell&optiSLang電機時空二維電磁力諧波優化設計案例
Ansys Maxwell&optiSLang電機時空二維電磁力諧波優化設計案例











評論