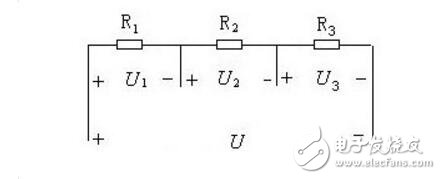
如果一個電阻器的兩個端子都連接到另一個電阻器的每個相應端子,則稱兩個電阻器并聯連接。在并聯電阻網絡中,電流可以采用多個路徑,這與串聯電阻器網絡不同,因為電流流動的路徑多條。因此,并聯電阻電路是分流器。
并聯電阻器
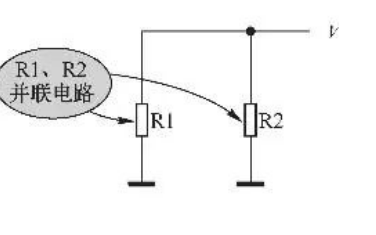
如果兩個或多個電阻并聯連接,則每個電阻器之間的電位差相同。并聯的電阻器連接到相同的節點。這可以通過存在多條電流流動路徑來識別。例如,下面顯示的電路是電阻器的并聯連接。電阻R1兩端的電位差與電阻R2兩端的電位差相同,等于電源電位VAB
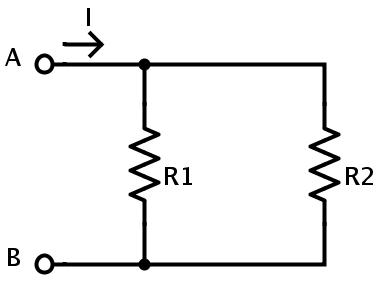
如果是VAB提供的潛力,那么
VR1=VR2=VAB
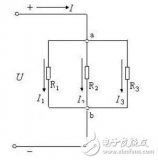
在下面的電路中,電阻R1、R2和R3并聯連接。

這里的供應潛力為VAB在點A和B之間。由于電阻R1、R2和R3并聯連接,因此每個電阻兩端的電位差與電源相同。因此VAB=VR1=VR2=VR3
VR1是電阻R1兩端的電位。
VR2是電阻R2兩端的電位。
VR3是電阻R3兩端的電位。
但是流過這三個電阻的電流是不同的。如果I是離開節點A的電流,那么它有三條路徑到達節點B。流過每個電阻的電流取決于其電阻。因此,在并聯電阻電路的情況下,所有電阻中的電流都不相同。如果I1是流過電阻R1的電流,I2是流過電阻R2的電流,I3是流過電阻R3的電流,那么電流I、I1、I2和I3可以在基爾霍夫電流定律的幫助下相關。根據基爾霍夫電流定律,“進入節點的電流總和等于離開節點的電流總和。
因此
I=I1+I2+I3。
等效電阻公式
以并聯組合方式連接的任意數量的電阻器都可以用單個電阻器代替,其電阻等于并聯組合電阻器的等效電阻。
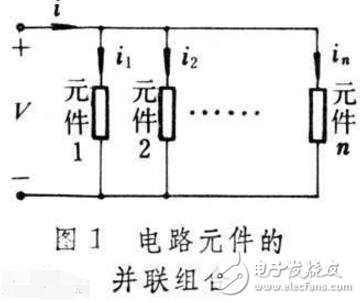
已經確定,并聯組合中每個電阻兩端的電壓是相同的,總電流等于單個電流的總和。請考慮以下電路。
這里,I=I1+I2+I3
I1=V/R1
I2=V/R2
I3=V/R3
如果RT是電路的總電阻,那么
I=V/RT
因此V/RT=V/R1+V/R2+V/R3
1/RT=1/R1+1/R2+1/R3
如果Req是電路的等效電阻,然后通過添加單個電阻的倒數(1/R)來計算。這個代數和的倒數將給出等效電阻。等效電阻R的公式eq如下圖所示,為N個電阻的并聯電阻電路。
(1/Req)=(1/R1)+(1/R2)+(1/R3)+.........+(1/rn)
從上式可以觀察到,并聯電阻的等效電阻總是小于最小電阻的電阻。
如果有兩個電阻并聯,則等效電阻為
(1/Req)=(1/R1)+(1/R2)
REQ=R1*R1/(R1+R2)
如果兩個電阻相等的電阻R并聯連接,則組合的等效電阻為R/2。
類似地,如果三個電阻相等的電阻R并聯連接,則組合的等效電阻為R/3。
電阻器的并聯連接給出了電導值。電導是電阻的倒數。它通常由符號G表示。電導的單位是西門子,由符號S表示,以前的電導單位是Mho(?),這是歐姆的反向拼寫,符號是Ω的顛倒表示。
即使并聯電阻連接在兩個節點之間,這種連接的表示也可以采用以下任何形式。

上述所有組合都是并聯電阻電路,并聯電阻的所有規則也適用于上述組合。
電流計算
并聯電阻電路每個分支中的電流彼此不同。由于每個電阻兩端的電壓相同,因此流過每個電阻的電流取決于該電阻的電阻。因此,如果一個分支中的電阻值與另一個分支不同,則這些分支中的電流將不同。該電流的值可以通過使用歐姆定律來確定。
考慮一個由兩個電阻組成的并聯網絡,電源電壓V在兩點A和B之間。
讓電流流過電阻R1是IR1和流過電阻R2的電流是IR2.
然后根據基爾霍夫電流定律,“進入電路的總電流等于離開電路的總電流。
如果IT是總電流,那么
IT=IR1+IR2
由于每個電阻兩端的壓降相同
IR1=V/R1
AndIR2=V/R2
如果考慮由n個電阻組成的并聯電阻電路,則電路中的總電流為
ITotal=IR1+IR2+….+IRn
如果串聯電阻電路稱為分壓器電路,則同樣,并聯電阻電路稱為分流電路。
如果考慮由n個具有不同電阻的電阻組成的并聯電阻電路,那么電流流動的路徑可能為n個不同的路徑,并且通過該路徑的電流值可能為n個不同的值。并聯組合的電阻可以互換,而不會影響總電流和等效電阻。
并聯電阻器示例
- 考慮以下電路,其中四個電阻R1、R2、R3和R4并聯連接。

每個電阻的電阻值為
R1=10Ω
R2=20Ω
R3=30Ω
R4=40Ω
電源電壓為V=24V
電路中的總電流可以通過兩種方法計算。
第一種方法是計算流過每個電阻的單個電流。
如果I1是流過電阻R1的電流,則根據歐姆定律
I1=V/R1=24/10=2.4A
同樣,如果I2是流過電阻R2的電流,則根據歐姆定律
I2=V/R2=24/20=1.2A
如果I3是流過電阻R3的電流,則根據歐姆定律
I3=V/R3=24/30=0.8A
如果I4是流過電阻R4的電流,那么根據歐姆定律
I4=V/R4=24/40=0.6A
如果我總是電路中的總電流,則根據基爾霍夫電流定律,
ITOTAL=I1+I2+I3+I4=2.4+1.2+0.8+0.6=5A
計算電流的第二種方法是找出電路的等效電阻。
電路的等效電阻為
1/REQ=(1/R1)+(1/R2)+(1/R3)+(1/R4)
1/REQ=(1/10)+(1/20)+(1/30)+(1/40)
REQ=1/2.083=4.8?
該單個電阻器可用于替換并聯組合中的所有電阻器。
∴ITOTAL=V/REQ=24/4.8=5A.
考慮以下電路,其中三個電阻R1、R2和R3并聯連接。

流過R1的電流為I1=6A
流過R2的電流為I2=4A
流過R3的電流為I3=2A
在并聯電阻電路中,每個電阻兩端的電壓相同,等于電源電壓。
此處的電源電壓為V=12V。
如果V1是電阻R1兩端的電壓,V2是電阻R2兩端的電壓,V3是電阻R3兩端的電壓,則
V=V1=V2=V3=12V
然后根據歐姆定律
R1=V1/I1
R1=12/6
R1=2?
R2=V2/I2
R2=12/4
R2=3?
R3=V3/I3
R3=12/2
R3=6?
應用
并聯電阻的概念用于惠斯通電橋電路的分析。并聯組合的電阻器用作分流器電路。這種分流器概念在模數轉換器和數模轉換器等應用中得到充分應用。
-
電阻器
+關注
關注
21文章
3796瀏覽量
62256 -
電源電壓
+關注
關注
2文章
991瀏覽量
24052 -
模數轉換器
+關注
關注
26文章
3218瀏覽量
126954 -
分流器
+關注
關注
2文章
140瀏覽量
18021 -
等效電阻
+關注
關注
7文章
60瀏覽量
11453
發布評論請先 登錄
相關推薦
電阻串聯與并聯有什么區別_電阻串聯和并聯的區別




 電子工程之并聯電阻
電子工程之并聯電阻




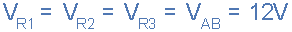










評論