筆者在日常的科研以及與課題組同學討論問題中發現,很多時候大家做的實驗測量可以被描述為“測電阻”。簡單的說,就是在一個樣品(如離子/電子導電陶瓷塊體或者薄膜)兩邊做上兩個電極,然后加電壓測試得到的電流。雖然這樣的操作雖然看起來極為簡單,但是由于我們經常面對的樣品常常是所謂的“混合離子-電子導體 (Mixed Ionic-Electronic Conductor,下文簡稱MIEC)”,這樣一個簡單的操作背后的物理圖像可能沒有大家想象得那么簡單。
本文就嘗試給大家介紹一下,如果你的樣品具有離子-電子混合導電(其實極為常見,甚至如不少導電聚合物、鹵素鈣鈦礦材料都是混合導體),那測到的電導率意味著什么,在樣品內部又發生了什么事情呢?
上述問題可以被抽象為圖1所示,一個MIEC樣品(例如很多能源轉換與儲存器件所用的材料等)放置于兩個電極中間,施加一個電壓(表示為U),我們會測到一個電流密度(用j表示)。
為了簡單起見,我們把問題簡化為一維,即假設電流密度在橫截面上每一點都是相等的。這一假設在使用平行板狀的電極(如一個陶瓷塊體樣品兩邊鍍上電極)是較為容易滿足的。在一維假設的基礎上,我們把兩個電極之間的樣品厚度用L表示。
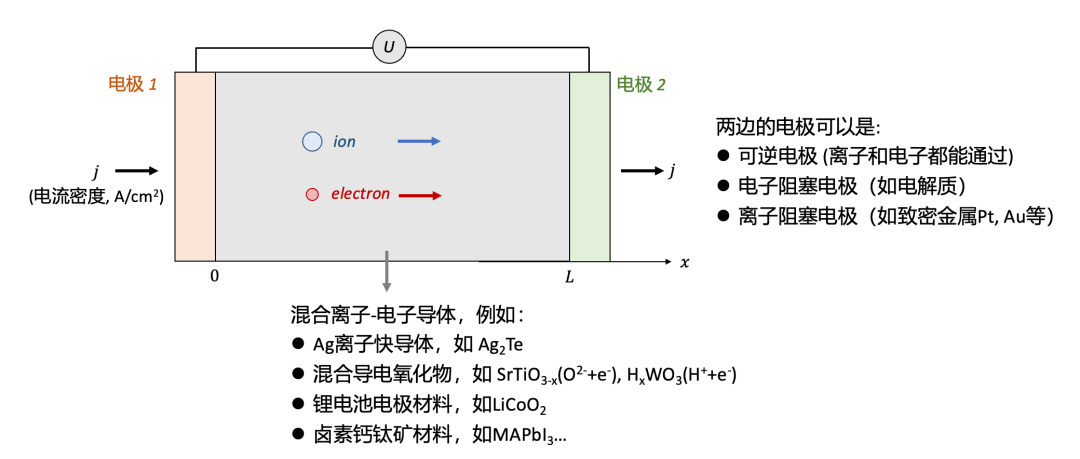
(圖1.混合離子-電子導體的導電率測量:電極的選擇)
首先我們需要解決的問題是電極的選擇。根據選擇的電極的不同,測量得到的電導率可能有極大的差異,而背后的物理化學過程也可能迥異。
一般說來,根據能通過的載流子種類的不同,電極可以分為三種:
可逆電極 (reversible electrode),即可以讓離子和電子都通過的電極。因此,通過可逆電極的電流可以既有電子電流,也有離子電流。
對于不同體系,可逆電極的選取不盡相同。例如,對于鋰電池材料(如LixFePO4, LixCoO2等),鋰金屬電極可以作為可逆電極。而對于高溫下混合導氧離子和電子的氧化物材料,多孔的鉑(Pt)金屬電極可以作為可逆電極。
電子阻塞電極 (electron-blocking electrode),即只能讓離子通過而電子無法通過的電極。如果用這種電極的話,通過電極的電流只能為離子電流。
常用的電子阻塞電極即為相應離子的電解質,如對于氧離子-電子混合導體,常用(Y,Zr)O2(YSZ)作為電子阻塞電極。值得提起注意的是,由于外電路導線只能讓電子流過,所以在電子阻塞電極的兩側還需要用可逆電極來使得電路完整。例如,如果用YSZ作為電極的話,還需要再加上多孔Pt作為電流收集層。
離子阻塞電極 (ion-blocking electrode),即只能讓電子通過而離子無法通過的電極。
在日常的實驗中,離子阻塞電極的使用非常普遍。例如,通過物理氣相沉積(Physical Vapor Deposition,PVD)如磁控濺射或者電子束蒸發制備的致密的Pt或者Au電極,往往是離子阻塞電極。下文中我們將看到,使用離子阻塞電極將不可避免地帶來MIEC內部的濃度極化。
從上面的討論我們可以看到,如果想要回答測到的電導率的物理意義這一問題,我們首先需要反問自己用的電極到底是屬于以上三類中的哪一類。電極的選擇會完全影響測量得到的電導率的含義(離子電導/電子電導/全電導),而且對于瞬態(transient)過程和穩態(steady state)下MIEC中的離子濃度分布也有極大影響。
下文中我們將根據電極的不同分為幾種情況討論:
我們先討論兩邊電極都是離子阻塞電極(如致密的Pt, Au等金屬電極)的情況,這或許是實驗中測量電導率大家最常遇到的電極情況。而對于電子阻塞電極,我們會發現情況與離子阻塞電極有相似之處,我們還將討論一端阻塞電子一端阻塞離子的情況。我們最后討論一端是可逆電極的情況,以及所謂的Hebb-Wagner法測量電導率。希望本文對于大家厘清一些固態離子學的基本概念有所幫助。
一、離子阻塞電極:物理圖像
我們首先討論兩邊電極都是離子阻塞電極的情況,如圖2中所示。為了討論方便,我們用氫化(hydrogenation)的氧化鎢(HxWO3,同時具有質子H^+^和電子e^-^導電)作為MIEC的一個例子。
兩邊的電極為致密的Pt薄膜,意味著只能讓電子通過而質子無法通過。可以想象,如果在兩端電極加一個電壓,離子和電子都會開始移動,但是兩端的電極只能讓電子通過,意味著通過電極的電流密度僅僅由電子電流構成。
我們想知道的是樣品中空間上每一點的化學組成(即H的含量,HxWO3中的x)隨著時間怎么變化,以及怎么把兩端加的電壓U和H的濃度變化聯系起來。
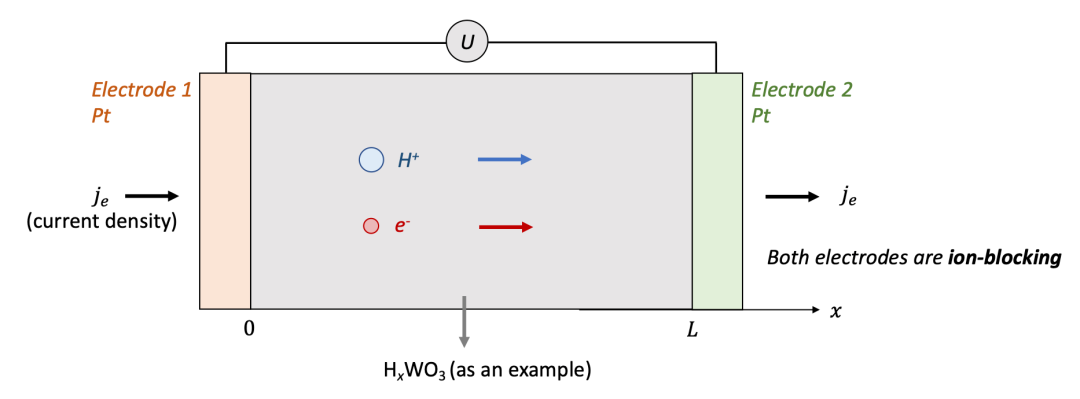
(圖2.離子阻塞電極的物理圖像)
根據離子和電子的漂移-擴散(Drift-diffusion)輸運方程(細節可以參看我們以前的公眾號文章:WESTON OpenCourse | 第三章:離子輸運的宏觀圖像與電化學勢),可以把電子和離子的電流表示用以下方程表示:
電子電流:
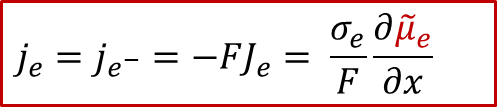
其中je是電子電流密度,而Je是電子的通量,σe代表電子導電率,最后一項位電子的電化學勢的梯度,注意電子的電荷ze-為+1)
離子電流:
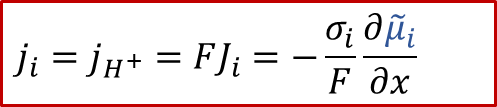
質子的電荷zH+為+1,σi代表離子導電率
由于離子電流為零(兩側是離子阻塞電極),所以我們有:

上面公式意味著,由于離子電流為零,MIEC中每一點的離子的電化學勢都一樣(梯度為0),而我們知道,對于任意一個電化學系統,兩側電極能測到電壓,說明兩側的電子的電化學勢不同,即:
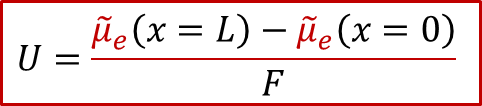
也就是說,兩側施加的電壓,造成了兩側電子的電化學勢的不同,而根據MIEC中局域每一點的電中性條件(我們后面會詳細討論為什么電中性條件是必要的),我們有:

再結合上面電壓的表達式,我們最終得到:

可以看見,外加的電壓最終轉換為了H的化學勢μ在MIEC兩端的差值,也就是說,外加的電壓造成了MIEC內部的H的濃度的不均勻,這也就是所謂 **濃度極化 ** (concentration polarization)。如果我們假設外加的電壓不是很大,并且MIEC滿足稀溶液假設(dilute limit),那么我們可以得到:
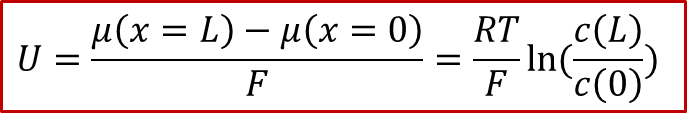
由于圖2所示的體系有中心對稱性,中心( *x * = L/2)處的濃度將保持為原有濃度,我們記為,我們同時把兩邊的濃度差值記為,那么我們可以得到電壓和濃度差值的關系:
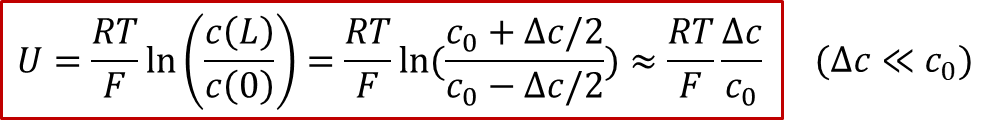
由此可見,由于兩邊的電極是離子阻塞電極,施加的電壓最終(在穩態下)會轉化為兩側的濃度差,因此電壓的本質是所謂“Nerstian”,即類似能斯特方程中的濃度項。
值得指出的是,上述討論可以類比到電子阻塞電極,唯一不同的是如果兩邊是電子阻塞電極的話,電子(而非離子)的電化學勢每一點都相等,兩邊的電壓差別變為用離子的電化學勢差表示。
二、電中性條件的必要性
在上面的討論中,很重要的一點是樣品中每一點都保持電中性,即帶正電的質子和帶負電的電子在每一點的濃度必須相等(濃度等于中性的 H 的濃度)。
粗看起來或許這有點違背直覺。筆者跟課題組的同學們討論的時候,很多同學的第一反應是:加一個電壓,帶正電的質子和帶負電的電子應該向相反方向移動從而造成所謂的“電荷分離”。
我們這里必須厘清一個非常重要的概念,即在MIEC中,除非在界面處等特殊情況,否則電中性的條件必須滿足,因此電子和離子的移動必須同時發生,即所謂的化學擴散(ambipolar chemical diffusion)。
下面我們就來看看為什么電中性條件必須滿足,或者說在一個較大的空間尺度上不滿足電中性會有什么后果。
泊松方程(Poisson’s equation)告訴我們,靜電勢的二階導數和凈電荷(正的減去負的)相關,如以下公式表示:
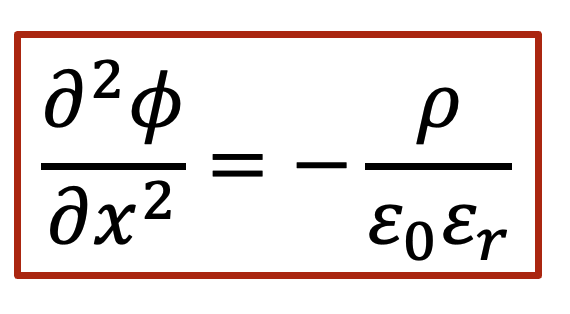
我們就根據泊松方程做一下所謂的“back-of-the-envelope calculation”,我們假設電中性條件如果不滿足,我們假設樣品里面有0.1 mol/L的正電荷(比如質子濃度相較電子濃度高出了0.1 mol/L),那么根據泊松方程,靜電勢的變化ΔV可以表示為(假設相對電容率為10):
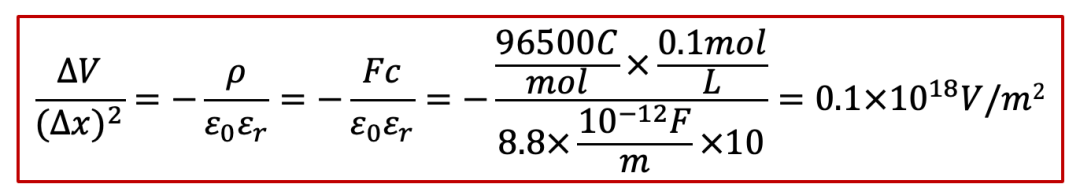
其中Δx是不滿足電中性的區域的長度(我們還是假設一維的情形)。那么,如果我們改變Δx,會有什么后果呢?如果我們計算ΔV和隨之而來造成的能量,我們可以得到下表(假設樣品橫截面積為1 cm^2^):

我們可以看見,如果把不滿足電中性的區域的尺度限制在納米級別,造成的電勢差已經達到1 V,這其實也就是我們經常見到的雙電層的情形,還是比較合理的。
但是如果不滿足電中性條件的區域超過納米尺度,事情就開始變得不合理了。如果尺度達到1 μm,電勢差已經達到MV級別,已經相當大了。而如果我們再極端一點,如果把尺度拉大到1 mm,那么相對應的能量已經遠遠超過1 TNT當量所對應的能量,這簡直太可怕了!
當然上面的極端情況顯然不能在我們測量的MIEC樣品中存在,上面的例子只是告訴大家,在絕大多數情況下,如果MIEC的載流子(離子+電子)濃度較高,MIEC的塊體(bulk)中都是滿足電中性條件的,只有在界面附近(或者晶界等“Extended defects”)有可能不滿足電中性。
這樣說明,在MIEC中的化學擴散(化學計量比或者濃度的變化)必須是離子和電子的協同擴散,而擴散較快的物種必須“等待”擴散較慢的物種從而保持局域的電中性。而回到我們上面兩邊都是離子阻塞電極的例子,每一點都滿足帶正電的質子和帶負電的電子濃度相等,所以其實電中性的H的濃度的變化也是化學擴散行為,由H^+^和e^- ^的協同擴散造成。
三、化學擴散和菲克定律:
解析濃度隨時間變化
上面的討論中,我們明確了兩端的電壓U和兩端的濃度差的關系,但是我們還想進一步知道施加電流/電壓過程中樣品中空間上每一點的濃度變化隨著時間演化的規律。
上文提到,兩端是離子阻塞電極的情況下,實際上樣品中的濃度變化與化學擴散的過程類似(由于電中性條件)。那么我們其實可以通過求解一個擴散方程來得到濃度(c(x,t),表明濃度是空間位置0
下面我們就簡單講講如何求解c(x,t),首先我們假設在兩側施加一個恒定的電流密度j,也就類似真實的實驗過程中我們用恒流源施加一個恒定電流,然后測量兩端的電壓U的變化。根據菲克第二定律,我們有:
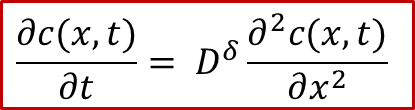
上式中**D^δ^**就是所謂的化學擴散系數,具體化學擴散系數的定義以及影響因素,可以參看我們另外一篇公眾號文章:WESTON OpenCourse | 第五章:擴散系數的類型及化學擴散。
為了求解以上的擴散方程,我們當然要明確體系的初始條件(t= 0的情形)和邊界條件( *x * = 0, L 的情況)。初始條件比較好解決,沒有外加電流之前,MIEC內部各處的H的濃度應該都是初始濃度c0,即:
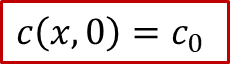
而邊界條件較為復雜,還是要從兩邊的電流入手,由于兩邊的電流都是電子電流(離子被阻塞),而且是一個恒定值j,我們有:
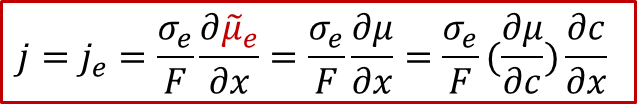
注意以上的公式只對于x= 0, L成立,我們可以反求出邊界條件:
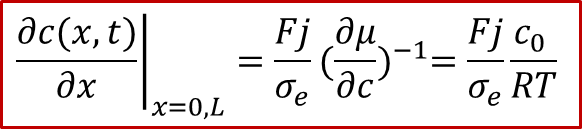
有了以上的初始和邊界條件,我們就可以求解擴散方程了。這里我們還需要假設所加的電流密度j比較小,引起的濃度變化不會改變D^δ^,否則方程解起來非常困難(只能數值解)。
在假設*D^δ^*恒定的基礎上,以上方程有解析解,如下所示(參考Yokota, J. Phys. Soc. Jpn., 1961):
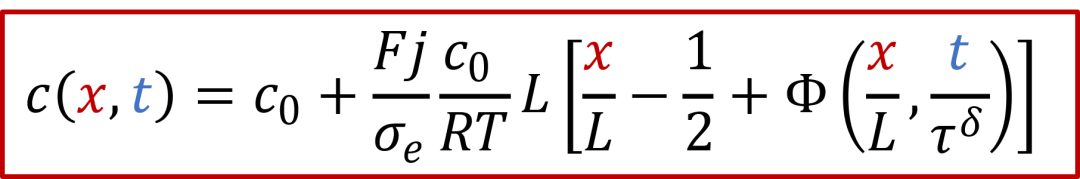
其中函數Φ有以下的表達式:
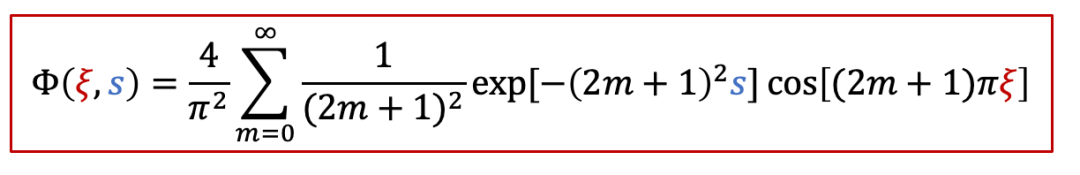
而c(x,t)表達式中有一個τ^δ^,其實這一項就是跟化學擴散相關的時間常數,我們知道擴散常數的單位是m ^2^ /s,因此*τ^δ^跟L^2^*成正比,即:
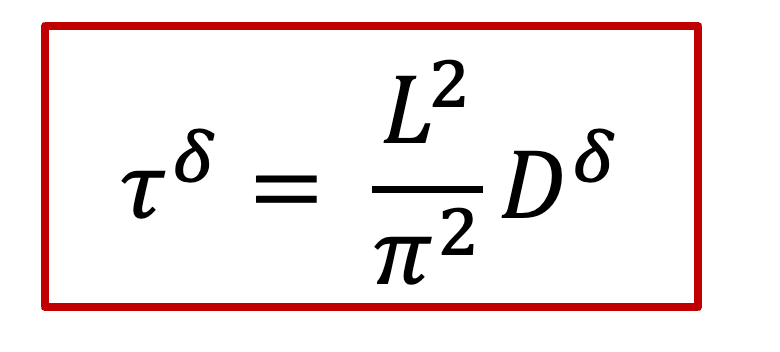
上面的解析解比較復雜,但是如果把x= 0, L帶入,不難看出這個解為什么成立。筆者這里強烈建議各位讀者動筆演算一下,相信能增加不少理解。
如果我們把解析解隨著時間t的演化畫出來,我們就能得到如圖3中所示的一系列曲線。
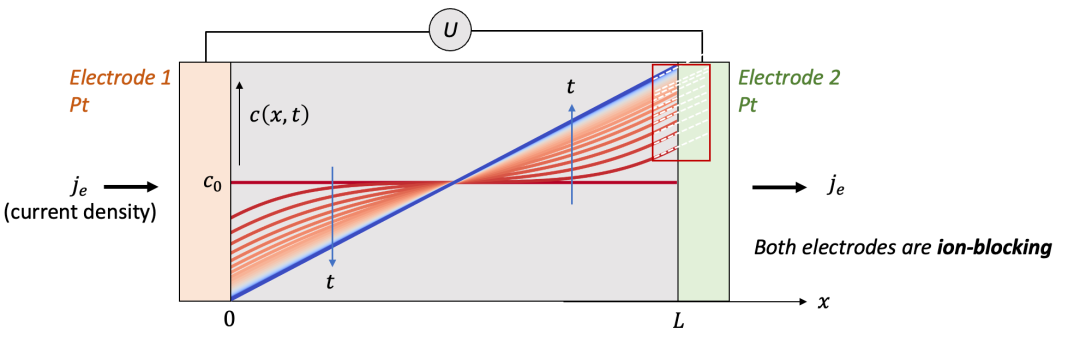
(圖3.MIEC中空間上每一點的濃度隨著時間的演化規律)
我們通過觀察這些曲線,可以發現幾個有意思的現象:
我們可以發現在樣品的邊界(x = 0, L,即圖3中右邊畫紅框處)c(x, t)的斜率(導數)在不同時間t都是一樣的。這是因為我們假設的邊界條件是恒定的電流密度j,因此兩個邊界上濃度隨著空間的導數都是不隨時間變化的。
我們可以想象一下,如果達到穩態(steady state,即t趨于無窮時的狀態)時,樣品內部的濃度分布應該是什么樣的呢?
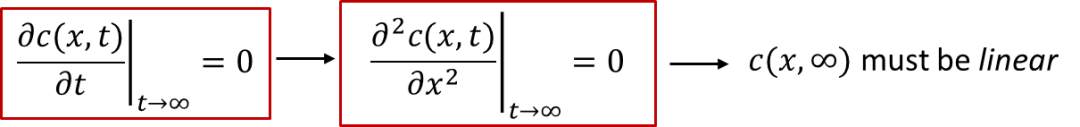
穩態下的定義是濃度不再隨時間變化,即:我們可以看到,由于濃度不再隨時間變化,c(x, t)對于x的二階導數應該為0,所以c(x, ∞)在空間上分布應該是一條斜線(線性分布),如圖3中藍色線條所示。
由于我們固定恒定電流密度j,由圖3可以看見,在瞬態(transient state)的演化過程中,兩側的濃度差不斷變大,這也就意味著,兩端測到的電壓U也是時間的函數(表示為U(t))。
如果我們還是假設體系滿足稀濃度條件(對于MIEC,即缺陷-缺陷相互作用可以忽略不計),那么我們其實可以計算出電壓U(t)的演化規律,由于:
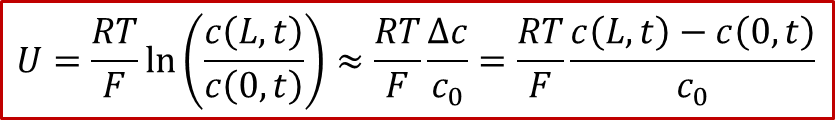
而通過c(x,t)的解析解,我們可以算出兩端的濃度差Δc隨著時間的變化,所以我們最終得到:
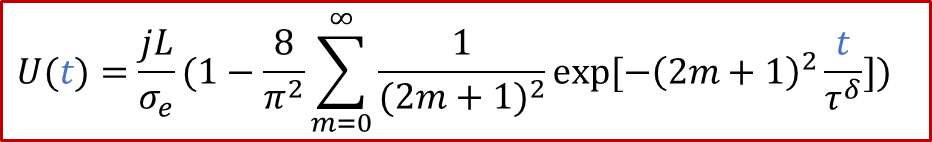
從上面的公式我們可以看出,兩端測到的電壓隨著時間是變化的。如果我們足夠有耐心等到穩態(t趨于無窮),可以得到:
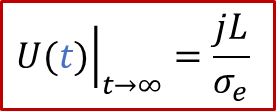
上面的公式其實就是歐姆定律(E = IR)的另外一種表現形式(注意j的單位是A/m ^2^ ),也表明由于用了阻塞電極,穩態下測到的電導其實就是只有電子電導σe的貢獻。而如果我們沒有那么耐心等無窮長時間,那么當t>> *τ^δ^*時,我們也有:
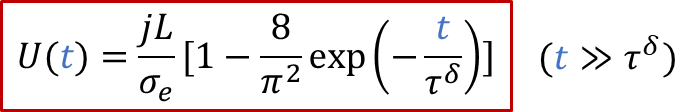
實驗上,我們可以有以下線性關系:
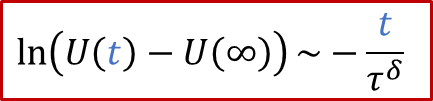
也就是說,我們按照上面做ln(U(t)-U(∞))和t二者之間的線性關系圖,根據斜率就可以求出τ^δ^,從而進一步推算出化學擴散系數D^δ^,這也提供了一種測量MIEC的化學擴散系數的電學方法。
四、電子阻塞電極+離子阻塞電極:
電化學儲能原理
上面我們詳細了討論兩邊電極都是離子阻塞電極的情形,那么一個自然的想法是,如果把一邊換為電子阻塞電極(如圖4所示),會有什么樣的不同呢?
我們還是以HxWO3為例,右邊還是用離子阻塞的致密Pt電極,左邊換為可以讓質子通過而阻塞電子的電極如Nafion等(前文也敘述過,最終外電路還是電子導通,所以需要一個可逆電極共同和電子阻塞電極使用)。
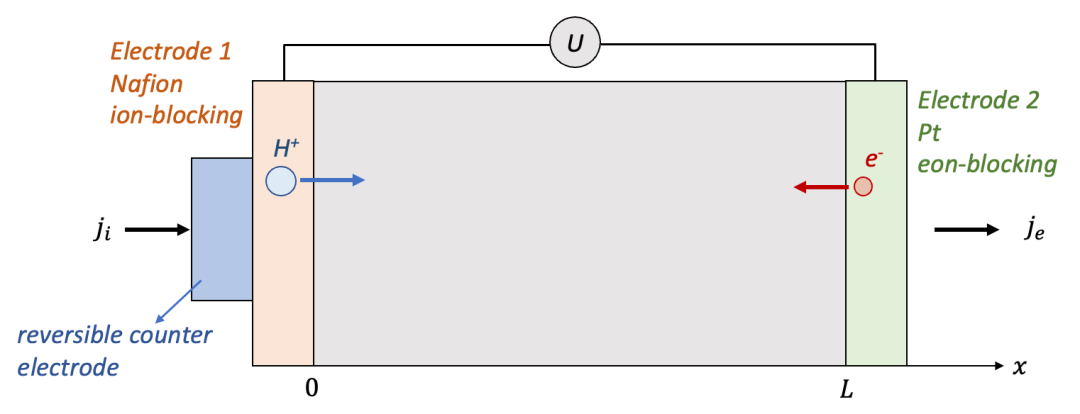
(圖4.電子阻塞電極(左)+離子阻塞電極(右)的情形)
跟上面的討論一樣,我們還是希望理解MIEC樣品中空間上每一點的H的濃度隨著時間如何變化。與兩端都是離子阻塞電極的情形一樣,電中性條件也是適用的,所以本質上還是求解擴散方程。同時,初始條件也沒有變化,即一開始樣品中每一點的濃度都是初始濃度c0,唯一有變化的是邊界條件。
此時兩邊電極不再對稱,我們仍然假設外加一個恒定的電流密度j,但是注意電流密度在左側電極變為只有離子電流ji,而在右側電極變為只有電子電流je,據此我們可以寫出邊界條件:
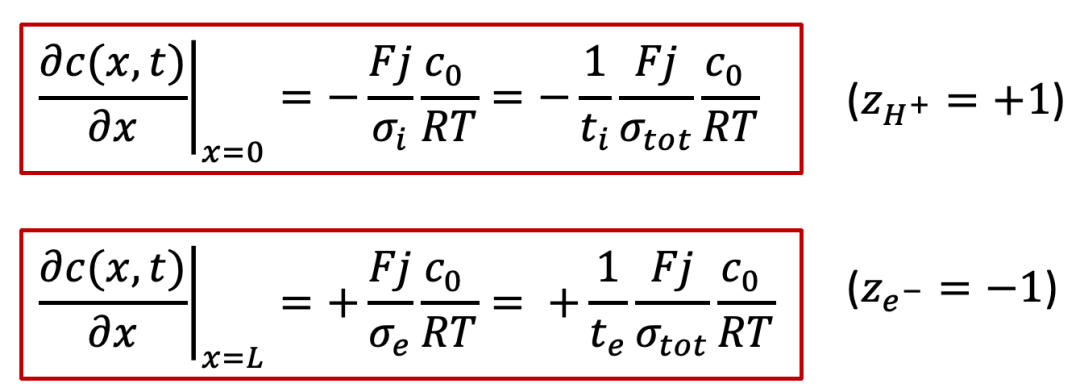
注意:上面符號的不同是由于質子和電子所帶電荷相反。
而且,我們可以觀察到,在兩個電極處的邊界條件除了符號相反,其實是相差了離子和電子的遷移數,遷移數的定義如下:
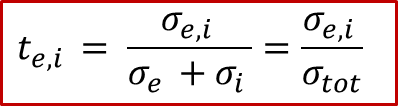
結合上面的初始和邊界條件,擴散方程也是有解析解的,但是實在是太過于復雜,筆者建議讀者參考相關文獻(如Preis and Sitte, J. Chem. Soc., Faraday Trans., 1996, 92(7), 1197-1203)。
我們這里想定性討論三種情況,如圖5所示(摘自Usiskin and Maier, PCCP, 20, 16449)。
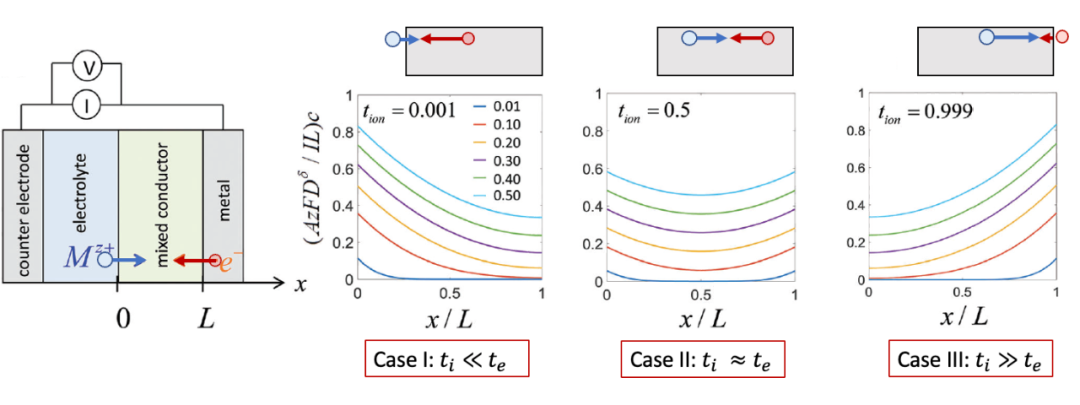
(圖5. 根據離子遷移數區分的三種不同的化學擴散情形)
adapted from Usiskin and Maier, PCCP, 20, 16449
電子遷移數te遠遠大于離子遷移數t~i ~的情形。
如圖5中Case I所示,我們想象一下,由于這種情況下電子“跑得快”,電子電導遠遠大于離子電導,因此化學擴散首先從左邊的界面,即電子阻塞電極處發生。
從上面的邊界條件也可以看出,由于ti~ ~ <
電子遷移數te與離子遷移數ti差不多,即“電子和離子跑得差不多快”。
在這種情況下,化學擴散從兩邊同時發生。由上面的邊界條件也可看出,這是兩邊的通量的絕對值相等。濃度隨時間演化的情況如圖5中Case II所示。
離子遷移數ti遠遠大于電子遷移數te的情形(t~i ~>>te)。
如圖5中Case III所示,這時候跟上述第一種情形反過來,由于這時離子跑得比電子快,所以化學擴散過程反而從右側界面發生。
其實上述過程,即由離子阻塞電極和電子阻塞電極共同存在的化學擴散情況在實際應用中非常普遍,最典型的就是鋰離子電池電極材料的充放電(離子嵌入intercalation)過程,如圖6所示。因此,這樣的過程其實是所有電化學儲能的基礎,因為涉及到把一個中性的物種(例如Li)拆分并分別輸運(例如Li^+^和e^-^)的過程。理解離子/電子阻塞電極因而對于理解電化學儲能的物理圖像有著非常重要的作用。
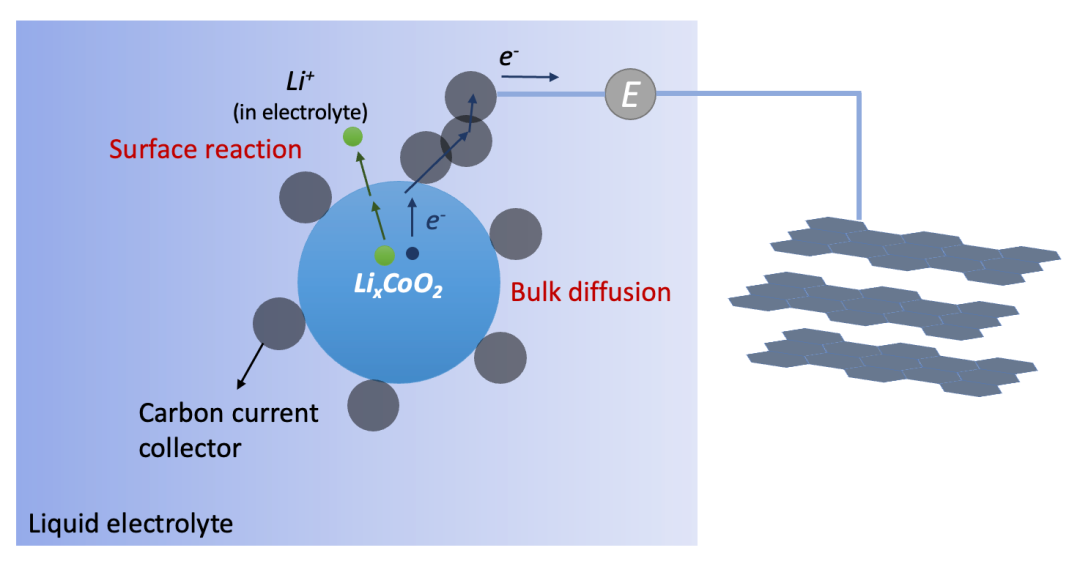
(圖6.鋰電池正極材料的充放電過程)
其實也是由離子阻塞電極(集流體)和電子阻塞電極(電解液)共同驅動的化學擴散過程
除了電化學儲能,其實這種阻塞電極的配置也非常普遍。我們舉另外一個關于有機半導體聚合物的例子。研究者發現其實很多有機導電(或者半導體)聚合物都是離子-電子混合導體,而離子電子的協同擴散(其實就是化學擴散)會影響這些有機聚合物的導電率的變化速度,同時也會影響其他物理性質比如透過率等。
今年最新發表在Nature Materials上的一篇文章,其實就是用了離子阻塞電極+電子阻塞電極研究了化學擴散過程(Keene et al., Nat. Mater. (2023),如圖7所示)。
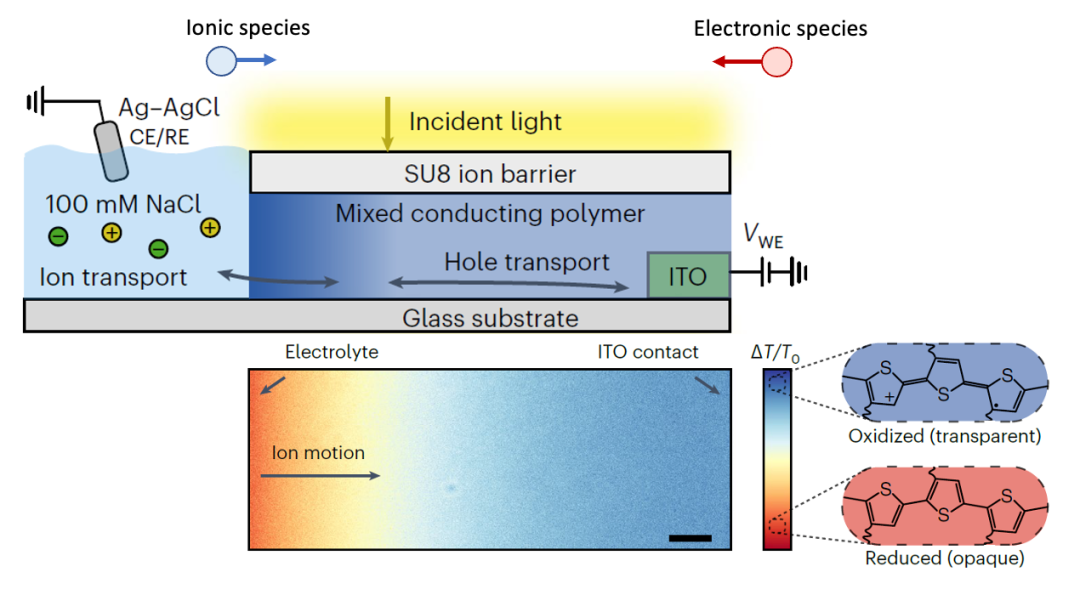
(圖7.導電聚合物中化學擴散對于光學透過率的影響)
adapted from Keene et al., Nat. Mater. (2023)
上圖所用的測量方法,其實就跟圖4中一樣,左邊是電子阻塞電極(電解質),右邊是離子阻塞電極(ITO電極)。在施加一個電壓以后,電中性物種(離子+電子)開始從左邊界面的化學擴散行為,改變電中性物種的濃度,從而改變導電聚合物的光學透過率。
這篇文章的作者們還詳細討論了什么情況下化學擴散從左邊界面開始(圖5中Case I),什么情況下從右邊界面開始(圖5中Case III)。所以其實很多材料體系,看似完全不同,其實內在的物理化學規律是一樣的,這也顯示出固態離子學知識的泛用性和重要性。
五、可逆電極:Hebb-Wagner法測試電導
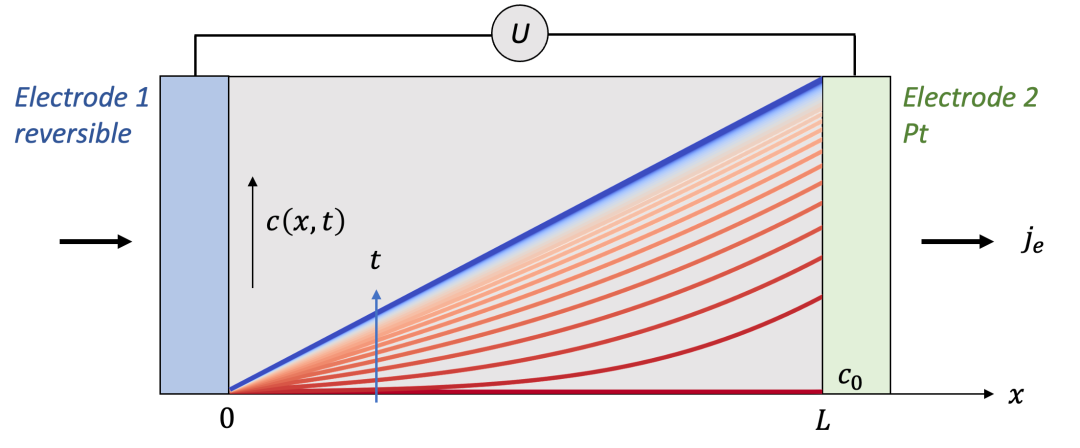
最后一部分我們來討論可逆電極的情況,我們還是以前面的兩邊都是離子阻塞電極出發,只是這時候我們把左邊的電極換為一個可逆電極。
這里我們以混合氧離子(O^2-^)和電子(e^-^)導體為例,如圖8所示。對于高溫下混合導通氧離子和電子的氧化物混合導體(例如(La,Sr)CoO3-x,(La,Sr)FeO3-x等,甚至對于電解質YSZ等都有一定但是非常小的電子電導率),致密的Pt電極可以認為是離子阻塞電極。而多孔Pt電極由于可以允許表面的氧交換反應,因而可以認為是可逆電極。
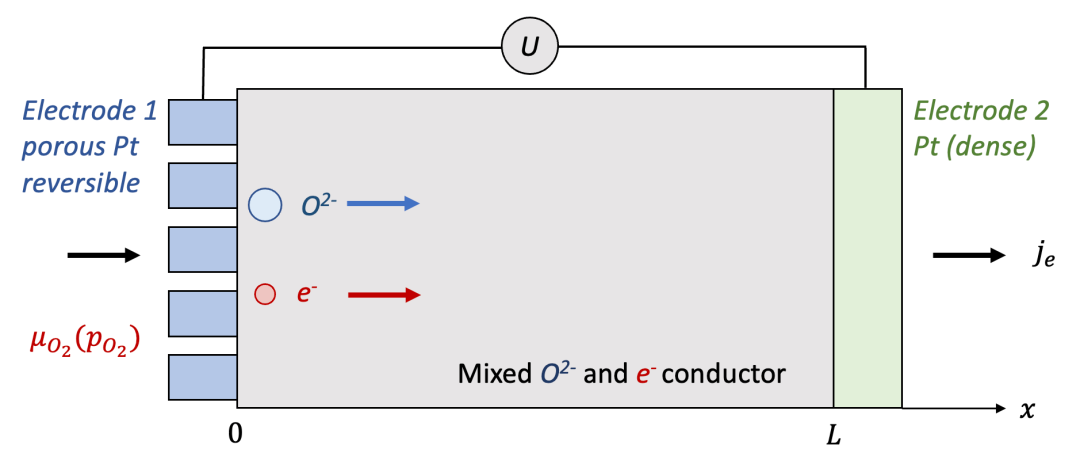
(圖8.左邊為可逆電極,右邊為離子阻塞電極的情形)
以氧離子+電子混合導體為例
我們還是想知道電中性的物種(這種情況下是O,即O^2-^ - 2e^-^)的濃度分布隨著時間的變化趨勢。讀者可能已經猜到了我們的套路,在外加驅動力不大的情況下,本質上還是求解化學擴散方程(同時假設化學擴散系數*D^δ^*為定值)。當然,跟前面唯一的不同在于可逆電極處的邊界條件的確定。其實結論非常簡單,在可逆電極處的濃度會保持初始濃度c0,即:
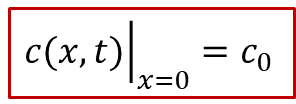
為什么呢?這是因為可逆電極因為可以同時導通離子和電子,因此平衡條件要求可逆電極的電中性物種的化學勢(比方說,對于氧化物就是氧電化學勢μO)與初始條件下c0對應的化學勢相等,因此在可逆電極處,濃度將保持不變,始終等于c0。
比如圖7中所示氧化物的例子,通常我們實驗中會把氧化物在一定的高溫下與外界的氧分壓(pO2)達到平衡,這時左邊的多孔Pt和氧化物的μO會達到相等。而后續在施加電流電壓的過程中,左邊可逆電極處由于還是跟外界的氧分壓pO2達到平衡,因此邊界條件要求此處氧的濃度保持初始濃度。
而右邊的離子阻塞電極處,邊界條件與上文討論中仍舊相同,即有:
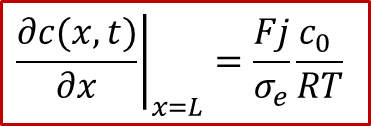
如果我們按照以上的邊界條件求解擴散方程,可以得到如圖9中所示的濃度分布演化規律c(x,t)。足夠細心的讀者可能已經發現,這種情況下的c(x,t)其實與圖3中所示的c(x,t)的右半部分一樣。這也是很合理的,因為如果兩邊都是離子阻塞電極,由于對稱性,x = L/2處得濃度會保持在初始濃度c0,與可逆電極處一樣。因此如果把一邊改為可逆電極,相當于從把兩邊都是離子阻塞電極得情況從中間“切開”,再在x方向上拉長到原來的兩倍而已。
(圖9.左邊為可逆電極,右邊為離子阻塞電極情形下的濃度分布時間演化規律)
到現在為止,我們為了求解擴散方程,都假設外加的電流或者電壓比較小,從而認為化學擴散系數D^δ^以及離子和電子的電導,即σi和σe都在樣品中各點都基本保持不變。在這種情況下,擴散方程的解析解比較容易獲得。
下面我們放寬這一限制,在圖8所示情況(左邊可逆電極,右邊離子阻塞電極,樣品為氧化物材料)下,我們施加一個較大的電壓U,大到足夠引起樣品中空間上各點的電子(或離子)電導不一致,我們會有什么發現呢?
這里我們以很多讀者非常熟悉的固體氧化物燃料電池電解質YSZ作為例子。YSZ雖然是離子導體(ti非常接近于1),但是也有一定的電子電導,相較于離子電導低很多,如圖10中右側Brouwer圖所示(如果對于Brouwer圖不太熟悉,請看我們之前的公眾號文章)。
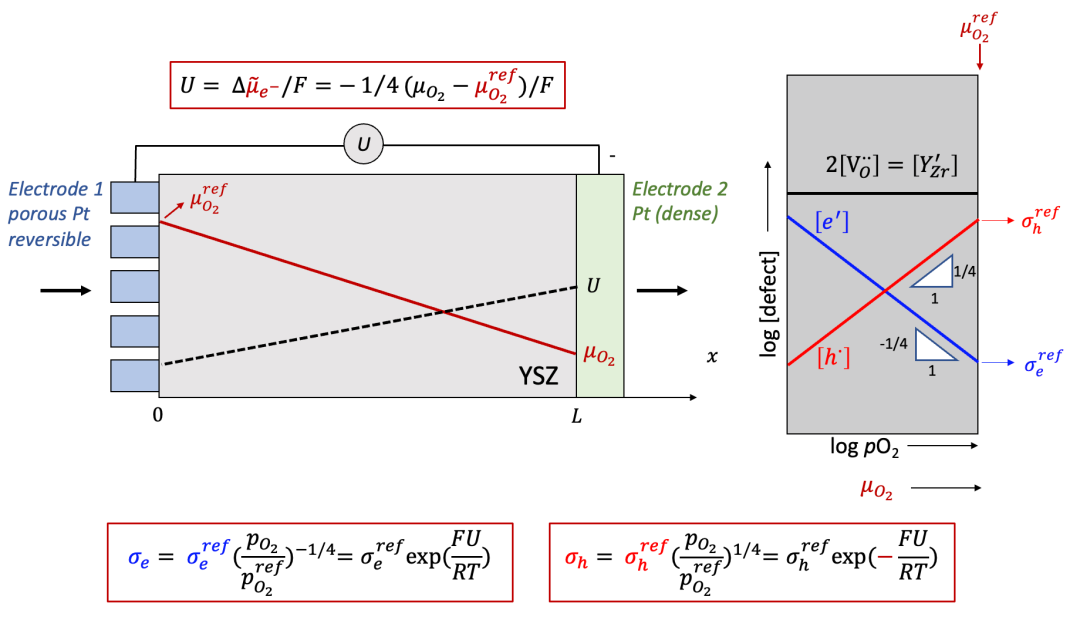
(圖10.Hebb-Wagner法測試YSZ的電子電導:Brouwer圖)
如果我們在右側的離子阻塞電極和左側的可逆電極之間加上一個電壓U,而且U比較大,會發生什么呢?我們可以通過以下幾點分析:
由于右邊的電極是離子阻塞,所以得到的電流還是電子電流,即離子電流為零,所以氧離子的電化學勢梯度也為0,那么我們通過電中性條件可以得到:
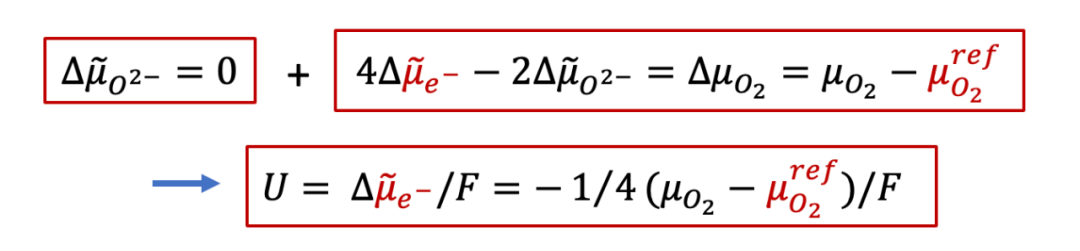
由上面公式可以看出,施加的U越大,樣品右側的氧的化學勢偏離左側可逆電極處的參比氧化學式(由初始氧的濃度決定)就越大,如圖9中所示。
由上面討論可以看出,施加電壓以后,樣品中每一點的氧的化學勢(或者等效氧分壓)不同,而如圖10中的Brouwer圖所示,YSZ的總電子電導由電子和空穴共同組成,而電子和空穴的濃度都是氧的化學勢的函數,可以表示為:

而空穴電導為:
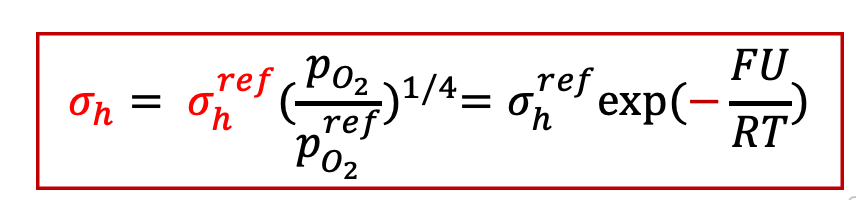
有了以上兩個觀察,我們最終關心的是施加一個電壓U后得到的電子電流密度如何計算。
由于電子電流由電子和空穴共同決定,因此我們需要計算電子和空穴電導的共同貢獻。注意電子和空穴電導在空間上每一點都是不一樣的,我們可以通過積分來計算,即從下面公式出發:
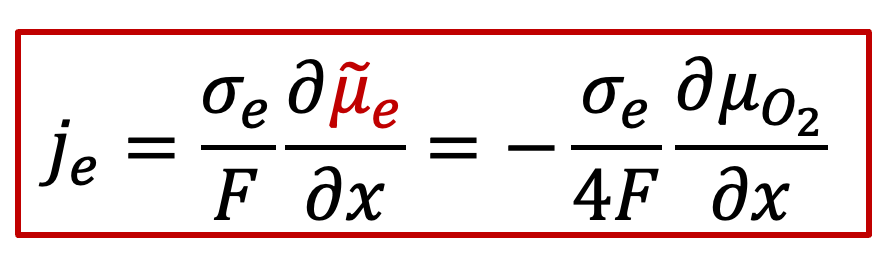
我們有:
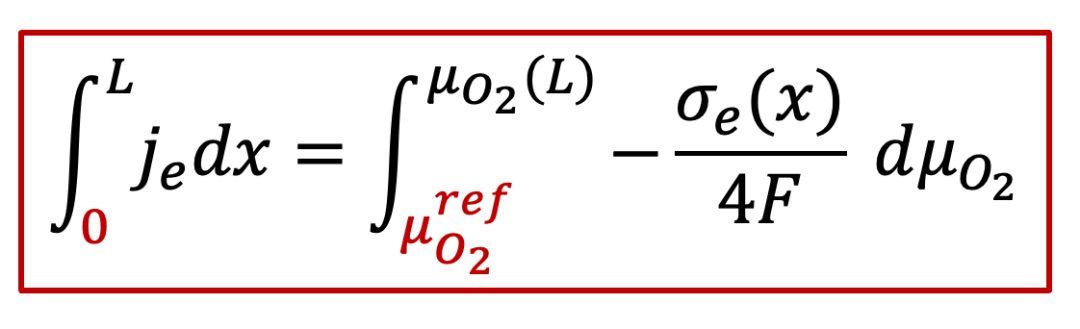
又由連續性條件,每一點的電流密度je都是一樣的,因此上面公式左邊就等于j~e ~L,因此,我們有:

空穴電導與上面的計算類似,所以總的電子電流密度jeon為:

上面的公式會有幾個很有趣的結果,比如,如果U比較小,那么我們知道exp(x)~1+x,我們可以得到:

這其實與上文中兩邊都是阻塞電極的情形類似,即在比較小的U的情況下,可以認為電子電導是不隨U變化而變化的,因此U和j之間成線性關系,滿足歐姆定律。
而如果U并不是很小,則U和j的曲線如圖11中所示。有趣的是,j在一定范圍內會基本不怎么增長,因為這時候進入了Brouwer圖中的所謂轉變區域(transition region),即從空穴導電占主導向電子導電占主導轉變。進一步增加U,則進入了電子導電占絕對主導的區域(空穴導電此時低了很多),而j基本上隨著U呈指數增長。
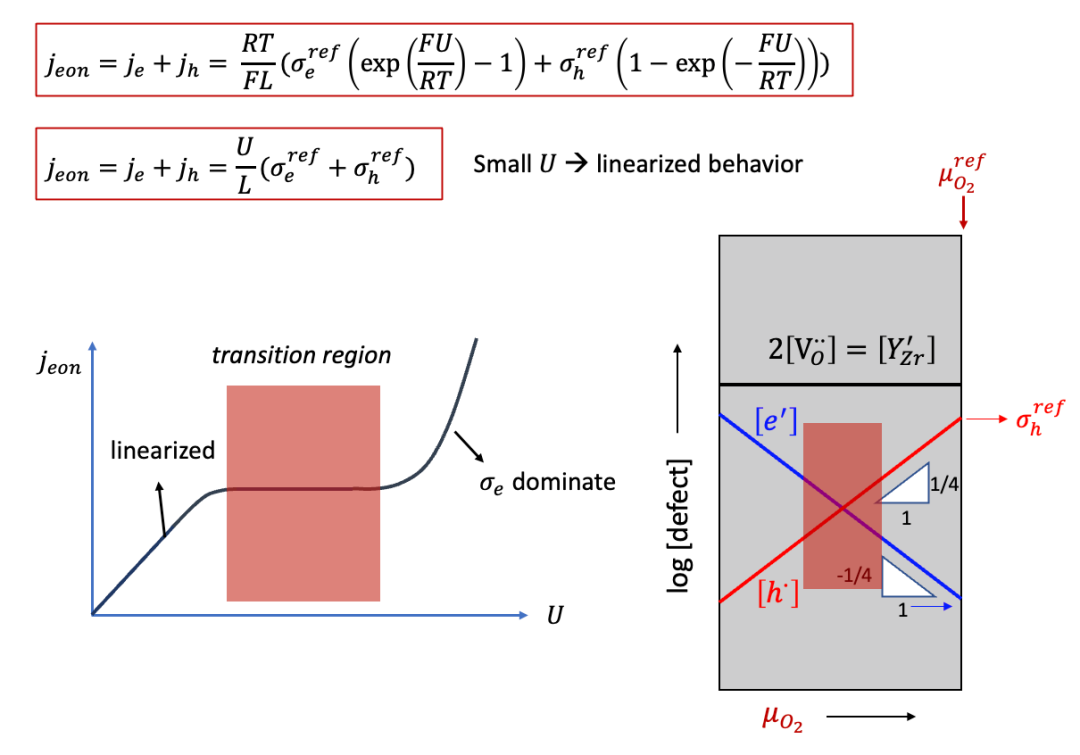
(圖11. Hebb-Wagner法測試YSZ的電子電導:電壓和外加電流之間的關系)
上述測量電子電導的方法,即一邊是可逆電極,一邊是離子阻塞電極的測量,一般被稱作Hebb-Wagner方法(最早由M. H. Hebb和C. Wagner兩位科學家分別獨立提出,因此得名)。
可以看出,這種方法是一種非常高效的測量電子電導隨著電化學勢變化趨勢的方法,因為只需要改變外加的電壓U就可以,而不用真的通過化學方法改變電化學勢。因此Hebb-Wagner方法在混合離子-電子導體的研究中得到了廣泛的應用。
當然,上面一個問題是需要知道電子(空穴)電導與化學勢之間的關系(即Brouwer圖中的斜率),這一限制可以放寬到僅僅假設一個power law,相關更深入的討論可以參考郭新教授和Maier教授的經典論文(Guo & Maier, Solid State Ionics 130, 267–280 (2000))。
六、總結
筆者希望讀者通過閱讀本文,能知道測量MIEC的電導率其實絕非易事(highly non-trivial),所以下次如果再接觸到混合離子-電子導體,讀者在施加一個電流(或電壓),測到一些數據后,如果能反問自己:我測到的數據到底意味著什么?帶著這個問題再來讀一遍本文,那筆者認為這篇文章的意義就達到了。這里我們簡單總結一下本文的一些知識點:
測試電極的選擇非常重要。
根據是否會選擇性地讓某種載流子通過,電極可以分為可逆電極(只導通離子+電子),離子阻塞電極(只導通電子)以及電子阻塞電極(只導通離子)。對于不同的MIEC體系,我們需要知道選擇的電極是屬于上述三種里面的哪一類。
電中性條件在MIEC的體相(bulk)中一定滿足,即便是有電壓/電流的情況下。這是后面求解化學擴散方程的基礎。
對于兩端都是離子阻塞電極的情況,測試得到的電流是電子電流,但是只有等到穩態下測到的電導率才是真實的電子電導率。如果外加的電流/電壓不太大,則在穩態下電中性物鐘的濃度分布是線性的。這是這種情況下濃度極化的規律。
對于一端阻塞電子一端阻塞離子的情況,需要分析電子和離子的遷移數的相對關系。這種情況也是電化學儲能的基礎。
對于一端是可逆電極,一端是離子阻塞電極的情況,這時我們可以施加一個較大的電壓來調控化學勢分布,從而得到電子電導隨著化學勢變化的規律。這一方法被稱作Hebb-Wagner測電導率法。
七、后記:一點歷史
正如本文開頭所說,萌生寫這篇文章的想法是因為跟課題組的同學們討論實驗結果和實驗設計。雖然之前筆者讀博士階段陸陸續續看過這方面的內容,但是為了寫這篇文章又去把一些“古早”文獻看了一些。基本所有文獻都會提到Yokota在上世紀五六十年代的開創性的工作,如圖12所示。
這兩篇60多年前的文章中基本涵蓋了本文的絕大部分討論,所以還是推薦大家去看看這些文獻(都發表在Journal of the Physical Society of Japan這一日本“國產”期刊上)。
這里再多說一句,我們處于一個信息和文獻都呈爆炸式增長的階段,但是“溯源”我覺得還是很有意義的。
筆者讀博士的時候,有一次參加一個會議,一位Keynote speaker在報告時候說“Every 30 years, we need to do the same things again, since the last generation of practitioners have already retired. (并非原話,不過大概是這個意思)”。聽眾聽完爆笑,不過可能大家都略有所思。我們的研究中不斷面臨著新的問題,但是知道前人做了什么,以及必要的時候知道很多細節,對于我們向前走和訓練學生也是非常重要的吧:)

(圖12.橫田伊佐秋(Isaaki Yokota)先生
在20世紀50、60年代的兩篇論文和熱力學著作)
筆者在網上并沒有找到太多關于橫田伊佐秋(Isaaki Yokota)這位學者的生平,只知道他是位凝聚態物理學家,1916年出生,1998年去世,學術生涯基本都在日本新瀉大學度過,也寫了不少重要的教科書(比如熱力學(圖12)和統計物理等)。如果哪位讀者了解更多這方面的歷史,還請不吝賜教。
審核編輯:湯梓紅
-
電流
+關注
關注
40文章
6937瀏覽量
132527 -
電極
+關注
關注
5文章
828瀏覽量
27287 -
能源
+關注
關注
3文章
1741瀏覽量
43590 -
導電率
+關注
關注
0文章
21瀏覽量
5657
原文標題:你真的知道你測到的電導率意味著什么嗎?——固態離子學基礎知識:阻塞電極和濃度極化
文章出處:【微信號:深圳市賽姆烯金科技有限公司,微信公眾號:深圳市賽姆烯金科技有限公司】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 固態離子學基礎知識:阻塞電極和濃度極化
固態離子學基礎知識:阻塞電極和濃度極化











評論