【編者按】這是一篇關于機器學習工具包Scikit-learn的入門級讀物。對于程序員來說,機器學習的重要性毋庸贅言。也許你還沒有開始,也許曾經失敗過,都沒有關系,你將在這里找到或者重拾自信。只要粗通Python,略知NumPy,認真讀完這21句話,逐行敲完示例代碼,就可以由此進入自由的王國。
作者 | 天元浪子
責編 | 歐陽姝黎
出品 | CSDN博客
01
機器學習有四種用途:分類、聚類、回歸和降維。
理解了這句話,就意味著學會了機器學習。迷茫的時候,在心里默念這句話,就會找到前進的方向。更嚴格一點,計算器學習的目的只有三個:分類、聚類和回歸,降維不過是達成目標的手段之一。
02
分類和聚類都是對個體樣本歸類,看起來很相似,實則相去甚遠——前者屬于有監督的學習,后者屬于無監督的學習。
分類是基于經驗的,而經驗來自過往的數據,這意味著分類需要訓練;聚類則是基于當前全部樣本的特征,不依賴經驗,自然也就無需訓練。舉個例子:讓你從一堆水果中挑出蘋果、橘子和香蕉,這是分類;讓你將畫在紙上的若干個圖案分組,分組規則由你決定,這是聚類。
03
從字面上看,分類和回歸看上去風馬牛不相及,其實二者是親兄弟,使用的算法幾乎完全重合。
分類是對個體樣本做出定性判定,回歸是對個體樣本做出定量判定,二者同屬于有監督的學習,都是基于經驗的。舉個例子:有經驗的老師預測某學生考試及格或不及格,這是分類;預測某學生能考多少分,這是回歸;不管是預測是否及格還是預測考多少分,老師的經驗數據和思考方法是相同的,只是最后的表述不同而已。
04
傳統的軟件開發,代碼是重點,而對于機器學習,數據是重點。
在訓練機器學習模型時,數據的質量和數量都會影響訓練結果的準確性和有效性。因此,無論是學習還是應用機器學習模型解決問題,前提都是要有足夠多且足夠好的數據集。
05
數據集通常是指由若干個樣本數據組成的二維數組,數組的每一行表示一個樣本的數據。
舉個例子:用性別、年齡、身高(米)、體重(千克)、職業、年薪(萬元)、不動產(萬元)、有價證券(萬元)等信息組成的一維數組表示一位征婚者的數據,下面的二維數組就是一個婚介機構收集到的征婚者數據集。
>>> import numpy as np>>> members = np.array([ ['男', '25', 185, 80, '程序員', 35, 200, 30], ['女', '23', 170, 55, '公務員', 15, 0, 80], ['男', '30', 180, 82, '律師', 60, 260, 300], ['女', '27', 168, 52, '記者', 20, 180, 150]])
06
數據集的列,也被成為特征維或特征列。
上面的征婚者數據集共有性別、年齡、身高(米)、體重(千克)、職業、年薪(萬元)、不動產(萬元)、有價證券(萬元)等8列,也可以說這個數據集有8個特征維或特征列。
07
所謂降維,并非是將數據集從二維變成一維,而是減少數據集的特征維。
征婚者的個人信息遠不止上面所列出的這8項,還可以加上生日、業余愛好、喜歡的顏色、愛吃的食物等等。不過,要是將所有的個人信息都加入到數據集中,不但會增加數據保存和處理的難度和成本,對于擇偶者來說,也會因為信息量太多而分散了注意力,以至于忽略了最重要的信息。降維就是從數據集中剔除對結果無影響或影響甚微的特征列。
08
標準化是對樣本集的每個特征列減去該特征列的平均值進行中心化,再除以標準差進行縮放。
滿分為100分的考試中,你如果得了90分,這自然是一個好成績。不過要是和其他同學比的話,就未必是了:假如其他同學都是滿分,那90分就是最差的一個。數據標準化的意義在于反映個體數據偏離所有樣本平均值的程度。下面是對征婚者數據集中有價證券特征列標準化后的結果。
>>> security = np.float32((members[:,-1])) # 提取有價證券特征列數據>>> securityarray([ 30., 80., 300., 150.], dtype=float32)>>> (security - security.mean())/security.std() # 減去均值再除以標準差array([-1.081241,-0.5897678,1.5727142,0.09829464],dtype=float32)
09
歸一化是對樣本集的每個特征列減去該特征列的最小值進行中心化,再除以極差(最大值最小值之差)進行縮放。
歸一化處理類似于標準化,結果收斂于[0,1]區間內。下面是對征婚者數據集中有價證券特征列歸一化后的結果。
>>> security = np.float32((members[:,-1])) # 提取有價證券特征列數據>>> securityarray([ 30., 80., 300., 150.], dtype=float32)>>> (security - security.min())/(security.max() - security.min()) # 減去最小值再除以極差array([0.,0.18518518,1.,0.44444445],dtype=float32)
10
機器學習模型只能處理數值數據,因此需要將性別、職業等非數值數據變成整數,這個過程被稱為特征編碼。
征婚者數據集中,對于性別特征列,可以用0表示女性,用1表示男性,或者反過來也沒有問題。不過這個方法不適用于職業特征列的編碼,因為不同職業之間原本是無序的,如果用這個方法編碼,就會產生2比1更接近3的問題。此時通行的做法是使用獨熱碼(one-of-K):若有n個不同的職業,就用n位二進制數字表示,每個數字只有1位為1其余為0。此時,職業特征列將從1個擴展為n個。下面使用Scikit-learn的獨熱碼編碼器對性別和職業兩列做特征編碼,生成6個特征列(性別2列,職業4列)。該編碼器位于preprocessing子模塊中。
>>> from sklearn import preprocessing as pp>>> X = [ ['男', '程序員'], ['女', '公務員'], ['男', '律師', ], ['女', '記者', ]]>>> ohe = pp.OneHotEncoder().fit(X)>>> ohe.transform(X).toarray()array([[0., 1., 0., 0., 1., 0.], [1., 0., 1., 0., 0., 0.], [0., 1., 0., 1., 0., 0.],[1.,0.,0.,0.,0.,1.]])
11
Scikit-learn的數據集子模塊datasets提供了若干數據集:函數名以load 開頭的是模塊內置的小型數據集;函數名以fetch開頭,是需要從外部數據源下載的大型數據集。
datasets.load_boston([return_X_y]) :加載波士頓房價數據集
datasets.load_breast_cancer([return_X_y]) :加載威斯康星州乳腺癌數據集
datasets.load_diabetes([return_X_y]) :加載糖尿病數據集
datasets.load_digits([n_class, return_X_y]) :加載數字數據集
datasets.load_iris([return_X_y]) :加載鳶尾花數據集。
datasets.load_linnerud([return_X_y]) :加載體能訓練數據集
datasets.load_wine([return_X_y]) :加載葡萄酒數據集
datasets.fetch_20newsgroups([data_home, …]) :加載新聞文本分類數據集
datasets.fetch_20newsgroups_vectorized([…]) :加載新聞文本向量化數據集
datasets.fetch_california_housing([…]) :加載加利福尼亞住房數據集
datasets.fetch_covtype([data_home, …]) :加載森林植被數據集
datasets.fetch_kddcup99([subset, data_home, …]) :加載網絡入侵檢測數據集
datasets.fetch_lfw_pairs([subset, …]) :加載人臉(成對)數據集
datasets.fetch_lfw_people([data_home, …]) :加載人臉(帶標簽)數據集
datasets.fetch_olivetti_faces([data_home, …]) :加載 Olivetti 人臉數據集
datasets.fetch_rcv1([data_home, subset, …]):加載路透社英文新聞文本分類數據集
datasets.fetch_species_distributions([…]) :加載物種分布數據集
12
每個二維的數據集對應著一個一維的標簽集,用于標識每個樣本的所屬類別或屬性值。通常數據集用大寫字母X表示,標簽集用小寫字母y表示。
下面的代碼從數據集子模塊datasets中提取了鳶尾花數據集——這是用來演示分類模型的最常用的數據集。鳶尾花數據集X共有150個樣本,每個樣本有4個特征列,分別使花萼的長度和寬度、花瓣的長度和寬度。這些樣本共有3種類型,分別用整數0、1、2表示,所有樣本的類型標簽組成標簽集y,這是一個一維數組。
>>> from sklearn.datasets import load_iris>>> X, y = load_iris(return_X_y=True)>>> X.shape # 數據集X有150個樣本,4個特征列(150, 4)>>> y.shape # 標簽集y的每一個標簽和數據集X的每一個樣本一一對應(150,)>>> X[0], y[0](array([5.1,3.5,1.4,0.2]),0)
加載數據時,如果指定return_X_y參數為False(默認值),則可以查看標簽的名字。
>>> iris = load_iris()>>> iris.target_names # 查看標簽的名字array(['setosa', 'versicolor', 'virginica'], dtype=')>>> X = iris.data>>>y=iris.target
13
模型訓練時,通常會將數據集和標簽集分成兩部分:一部分用于訓練,一部分用于測試。
分割數據集是一項非常重要的工作,不同的分割方法對于模型訓練的結果有不同的影響。Scikit-learn提供了很多種數據集分割方法,train_test_split是其中最簡單的一種,可以根據指定的比例隨機抽取測試集。train_test_split函數位于模型選擇子模塊model_selection中。
>>> from sklearn.datasets import load_iris>>> from sklearn.model_selection import train_test_split as tsplit>>> X, y = load_iris(return_X_y=True)>>> X_train, X_test, y_train, y_test = tsplit(X, y, test_size=0.1)>>> X_train.shape, X_test.shape((135, 4), (15, 4))>>> y_train.shape, y_test.shape((135,),(15,))
上面的代碼按照10%的比例隨機從數據集中抽取樣本作為測試集,剩余樣本作為訓練集。分割完成后,訓練集有135個樣本,測試集有15個樣本。
14
近朱者赤,近墨者黑,距離誰最近,就和誰同類——這就是k-近鄰分類。
k-近鄰分類是最簡單、最容易的分類方法。對于待分類的樣本,從訓練集中找出k個和它距離最近的樣本,考察這些樣本中哪一個標簽最多,就給待分類樣本貼上該標簽。k值的最佳選擇高度依賴數據,較大的k值會抑制噪聲的影響,但同時也會使分類界限不明顯。通常k值選擇不大于20的整數。
>>> from sklearn.datasets import load_iris>>> from sklearn.model_selection import train_test_split as tsplit>>> from sklearn.neighbors import KNeighborsClassifier # 導入k-近鄰分類模型>>> X, y = load_iris(return_X_y=True) # 獲取鳶尾花數據集,返回樣本集和標簽集>>> X_train, X_test, y_train, y_test = tsplit(X, y, test_size=0.1) # 拆分為訓練集和測試集>>> m = KNeighborsClassifier(n_neighbors=10) # 模型實例化,n_neighbors參數指定k值,默認k=5>>> m.fit(X_train, y_train) # 模型訓練KNeighborsClassifier()>>> m.predict(X_test) # 對測試集分類array([2, 1, 2, 2, 1, 2, 1, 2, 2, 1, 0, 1, 0, 0, 2])>>> y_test # 這是實際的分類情況,上面的預測只錯了一個array([2, 1, 2, 2, 2, 2, 1, 2, 2, 1, 0, 1, 0, 0, 2])>>> m.score(X_test, y_test) # 模型測試精度(介于0~1)0.9333333333333333
應用分類模型對15個測試樣本分類,結果只有1個是錯誤的,準確率約為93%。在分類算法中,score是最常用的評估函數,返回分類正確的樣本數與測試樣本總數之比。
15
一輛開了八年的大切諾基可以賣多少錢?最簡單的方法是參考k輛同款車型且使用年限相近的二手車售價的均值——這就是k-近鄰回歸。
k-近鄰算法不僅可以用來解決分類問題,也可以用來解決回歸問題。k-近鄰回歸預測樣本的標簽由它最近鄰標簽的均值計算而來。下面的代碼以波士頓房價數據集為例,演示了k-近鄰回歸模型的用法。波士頓房價數據集統計的是20世紀70年代中期波士頓郊區房價的中位數,一共有506條不同的數據,每條數據包含區域的人文環境、自然環境、商業環境、交通狀況等13個屬性,標簽是區域房價的平均值。
>>> from sklearn.datasets import load_boston>>> from sklearn.model_selection import train_test_split as tsplit>>> from sklearn.neighbors import KNeighborsRegressor>>> X, y = load_boston(return_X_y=True) # 加載波士頓房價數據集>>> X.shape, y.shape, y.dtype # 該數據集共有506個樣本,13個特征列,標簽集為浮點型,適用于回歸模型((506, 13), (506,), dtype('float64'))>>> X_train, X_test, y_train, y_test = tsplit(X, y, test_size=0.01) # 拆分為訓練集和測試集>>> m = KNeighborsRegressor(n_neighbors=10) # 模型實例化,n_neighbors參數指定k值,默認k=5>>> m.fit(X_train, y_train) # 模型訓練KNeighborsRegressor(n_neighbors=10)>>> m.predict(X_test) # 預測6個測試樣本的房價array([27.15, 31.97, 12.68, 28.52, 20.59, 21.47])>>> y_test # 這是測試樣本的實際價格,除了第2個(索引為1)樣本偏差較大,其他樣本偏差還算差強人意array([29.1,50.,12.7,22.8,20.4,21.5])
16
常用的回歸模型的評價方法有均方誤差、中位數絕對誤差和復相關系數等。
評價一個回歸結果的優劣,比評價一個分類結果要困難得多——前者需要考慮偏離程度,而后者只考慮對錯。常用的回歸評價函數是均方誤差函數、中位數絕對誤差函數和復相關系數函數等,這幾個函數均被包含在模型評估指標子模塊metrics中。均方誤差和中位數絕對誤差越小,說明模型精確度越高;復相關系數則相反,越接近1說明模型精確度越高,越接近0說明模型越不可用。
以上一段代碼為例,模型評估結果如下。
>>> from sklearn import metrics>>> y_pred = m.predict(X_test)>>> metrics.mean_squared_error(y_test, y_pred) # 均方誤差60.27319999999995>>> metrics.median_absolute_error(y_test, y_pred) # 中位數絕對誤差1.0700000000000003>>> metrics.r2_score(y_test, y_pred) # 復相關系數0.5612816401629652
復相關系數只有0.56,顯然,用k-近鄰算法預測波士頓房價不是一個好的選擇。下面的代碼嘗試用決策樹算法預測波士頓房價,得到了較好的效果,復相關系數達到0.98,預測房價非常接近實際價格,誤差極小。
>>> from sklearn.datasets import load_boston>>> from sklearn.model_selection import train_test_split as tsplit>>> from sklearn.tree import DecisionTreeRegressor>>> X, y = load_boston(return_X_y=True) # 加載波士頓房價數據集>>> X_train, X_test, y_train, y_test = tsplit(X, y, test_size=0.01) # 拆分為訓練集和測試集>>> m = DecisionTreeRegressor(max_depth=10) # 實例化模型,決策樹深度為10>>> m.fit(X, y) # 訓練DecisionTreeRegressor(max_depth=10)>>> y_pred = m.predict(X_test) # 預測>>> y_test # 這是測試樣本的實際價格,除了第2個(索引為1)樣本偏差略大,其他樣本偏差較小array([20.4, 21.9, 13.8, 22.4, 13.1, 7. ])>>> y_pred # 這是6個測試樣本的預測房價,非常接近實際價格array([20.14, 22.33, 14.34, 22.4, 14.62, 7. ])>>> metrics.r2_score(y_test, y_pred) # 復相關系數0.9848774474870712>>> metrics.mean_squared_error(y_test, y_pred) # 均方誤差0.4744784865112032>>> metrics.median_absolute_error(y_test, y_pred) # 中位數絕對誤差0.3462962962962983
17
決策樹、支持向量機(SVM)、貝葉斯等算法,既可以解決分類問題,也可以解決回歸問題。
應用這些算法解決分類和回歸問題的流程,與使用k-近鄰算法基本相同,不同之處在于不同的算法提供了不同的參數。我們需要仔細閱讀算法文檔,搞清楚這些參數的含義,選擇正確的參數,才有可能得到正確的結果。比如,支持向量機(SVM)的回歸模型參數中,比較重要的有kernel參數和C參數。kernel參數用來選擇內核算法;C是誤差項的懲罰參數,取值一般為10的整數次冪,如 0.001、0.1、1000 等。通常,C值越大,對誤差項的懲罰越大,因此訓練集測試時準確率就越高,但泛化能力越弱;C值越小,對誤差項的懲罰越小,因此容錯能力越強,泛化能力也相對越強。
下面的例子以糖尿病數據集為例,演示了支持向量機(SVM)回歸模型中不同的C參數對回歸結果的影響。糖尿病數據集收集了442 例糖尿病患者的10 個指標(年齡、性別、體重指數、平均血壓和6 個血清測量值),標簽是一年后疾病進展的定量測值。需要特別指出,糖尿病數據集并不適用于SVM算法,此處僅是為了演示參數選擇如何影響訓練結果。
>>> from sklearn.datasets import load_diabetes>>> from sklearn.model_selection import train_test_split as tsplit>>> from sklearn.svm import SVR>>> from sklearn import metrics>>> X, y = load_diabetes(return_X_y=True)>>> X.shape, y.shape, y.dtype((442, 10), (442,), dtype('float64'))>>> X_train, X_test, y_train, y_test = tsplit(X, y, test_size=0.02)>>> svr_1 = SVR(kernel='rbf', C=0.1) # 實例化SVR模型,rbf核函數,C=0.1>>> svr_2 = SVR(kernel='rbf', C=100) # 實例化SVR模型,rbf核函數,C=100>>> svr_1.fit(X_train, y_train) # 模型訓練SVR(C=0.1)>>> svr_2.fit(X_train, y_train) # 模型訓練SVR(C=100)>>> z_1 = svr_1.predict(X_test) # 模型預測>>> z_2 = svr_2.predict(X_test) # 模型預測>>> y_test # 這是測試集的實際值array([ 49., 317., 84., 181., 281., 198., 84., 52., 129.])>>> z_1 # 這是C=0.1的預測值,偏差很大array([138.10720127, 142.1545034 , 141.25165838, 142.28652449, 143.19648143, 143.24670732, 137.57932272, 140.51891989, 143.24486911])>>> z_2 # 這是C=100的預測值,偏差明顯變小array([ 54.38891948, 264.1433666 , 169.71195204, 177.28782561, 283.65199575, 196.53405477, 61.31486045, 199.30275061, 184.94923477])>>> metrics.mean_squared_error(y_test, z_1) # C=0.01的均方誤差8464.946517460194>>> metrics.mean_squared_error(y_test, z_2) # C=100的均方誤差3948.37754995066>>> metrics.r2_score(y_test, z_1) # C=0.01的復相關系數0.013199351909129464>>> metrics.r2_score(y_test, z_2) # C=100的復相關系數0.5397181166871942>>> metrics.median_absolute_error(y_test, z_1) # C=0.01的中位數絕對誤差57.25165837797314>>> metrics.median_absolute_error(y_test, z_2) # C=100的中位數絕對誤差22.68513954888364
18
隨機森林是將多棵分類決策樹或者回歸決策樹集成在一起的算法,是機器學習的一個分支——集成學習的方法。
以隨機森林分類為例,隨機森林包含的每棵決策樹都是一個分類模型,對于一個輸入樣本,每個分類模型都會產生一個分類結果,類似投票表決。隨機森林集成了所有的投票分類結果,并將被投票次數最多的類別指定為最終的輸出類別。隨機森林每顆決策樹的訓練樣本都是隨機的,決策樹中訓練集的特征列也是隨機選擇確定的。正是因為這兩個隨機性的存在,使得隨機森林不容易陷入過擬合,并且具有很好的抗噪能力。
考慮到隨機森林的每一棵決策樹中訓練集的特征列是隨機選擇確定的,更適合處理具有多特征列的數據,這里選擇 Scikit-learn內置的威斯康星州乳腺癌數據集來演示隨機森林分類模型的使用。該數據集有 569 個乳腺癌樣本,每個樣本包含半徑、紋理、周長、面積、是否平滑、是否緊湊、是否凹凸等 30 個特征列。
>>> from sklearn.datasets import load_breast_cancer # 導入數據加載函數>>> from sklearn.tree import DecisionTreeClassifier # 導入隨機樹>>> from sklearn.ensemble import RandomForestClassifier # 導入隨機森林>>> from sklearn.model_selection import cross_val_score # 導入交叉驗證>>> ds = load_breast_cancer() # 加載威斯康星州乳腺癌數據集>>> ds.data.shape # 569個乳腺癌樣本,每個樣本包含30個特征(569, 30)>>> dtc = DecisionTreeClassifier() # 實例化決策樹分類模型>>> rfc = RandomForestClassifier() # 實例化隨機森林分類模型>>> dtc_scroe = cross_val_score(dtc, ds.data, ds.target, cv=10) # 交叉驗證>>> dtc_scroe # 決策樹分類模型交叉驗證10次的結果array([0.92982456, 0.85964912, 0.92982456, 0.89473684, 0.92982456, 0.89473684, 0.87719298, 0.94736842, 0.92982456, 0.92857143])>>> dtc_scroe.mean() # 決策樹分類模型交叉驗證10次的平均精度0.9121553884711779>>> rfc_scroe = cross_val_score(rfc, ds.data, ds.target, cv=10) # 交叉驗證>>> rfc_scroe # 隨機森林分類模型交叉驗證10次的結果array([0.98245614, 0.89473684, 0.94736842, 0.94736842, 0.98245614, 0.98245614, 0.94736842, 0.98245614, 0.94736842, 1. ])>>> rfc_scroe.mean()# 隨機森林分類模型交叉驗證10次的平均精度0.9614035087719298
上面的代碼使用了交叉驗證法,其原理是將樣本分成n份,每次用其中的n-1份作訓練集,剩余1份作測試集,訓練n次,返回每次的訓練結果。結果顯示,同樣交叉驗證10次,96%對91%,隨機森林的分類準確率明顯高于隨機樹。
19
基于質心的聚類,無論是k均值聚類還是均值漂移聚類,其局限性都是顯而易見的:無法處理細長條、環形或者交叉的不規則的樣本分布。
k均值(k-means)聚類通常被視為聚類的“入門算法”,其算法原理非常簡單。首先從X數據集中選擇k個樣本作為質心,然后重復以下兩個步驟來更新質心,直到質心不再顯著移動為止:第一步將每個樣本分配到距離最近的質心,第二步根據每個質心所有樣本的平均值來創建新的質心。
基于質心的聚類是通過把樣本分離成多個具有相同方差的類的方式來聚集數據的,因此總是希望簇是凸(convex)的和各向同性(isotropic)的,但這并非總是能夠得到滿足。例如,對細長、環形或交叉等具有不規則形狀的簇,其聚類效果不佳。
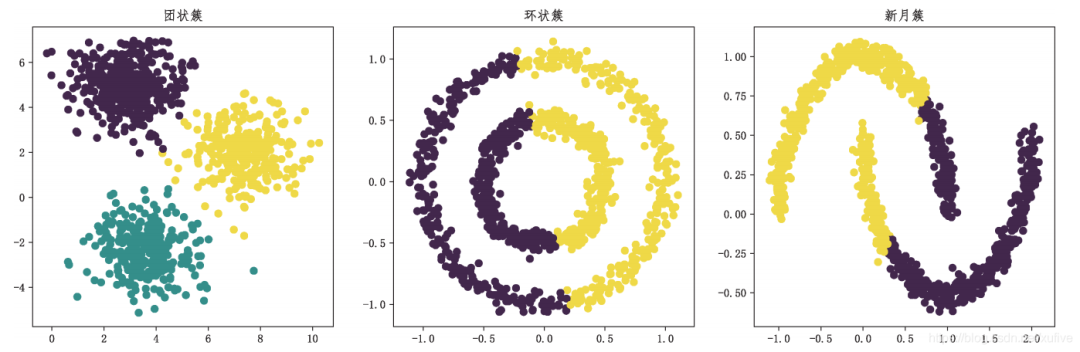
>>> from sklearn import datasets as dss # 導入樣本生成器>>> from sklearn.cluster import KMeans # 從聚類子模塊導入聚類模型>>> import matplotlib.pyplot as plt>>> plt.rcParams['font.sans-serif'] = ['FangSong']>>> plt.rcParams['axes.unicode_minus'] = False>>> X_blob, y_blob = dss.make_blobs(n_samples=[300,400,300], n_features=2)>>> X_circle, y_circle = dss.make_circles(n_samples=1000, noise=0.05, factor=0.5)>>> X_moon, y_moon = dss.make_moons(n_samples=1000, noise=0.05)>>> y_blob_pred = KMeans(init='k-means++', n_clusters=3).fit_predict(X_blob)>>> y_circle_pred = KMeans(init='k-means++', n_clusters=2).fit_predict(X_circle)>>> y_moon_pred = KMeans(init='k-means++', n_clusters=2).fit_predict(X_moon)>>> plt.subplot(131)0x00000180AFDECB88>>>> plt.title('團狀簇')Text(0.5, 1.0, '團狀簇')>>> plt.scatter(X_blob[:,0], X_blob[:,1], c=y_blob_pred)0x00000180C495DF08>>>> plt.subplot(132)0x00000180C493FA08>>>> plt.title('環狀簇')Text(0.5, 1.0, '環狀簇')>>> plt.scatter(X_circle[:,0], X_circle[:,1], c=y_circle_pred)0x00000180C499B888>>>> plt.subplot(133)0x00000180C4981188>>>> plt.title('新月簇')Text(0.5, 1.0, '新月簇')>>> plt.scatter(X_moon[:,0], X_moon[:,1], c=y_moon_pred)0x00000180C49DD1C8>>>>plt.show()
上面的代碼首先使用樣本生成器生成團狀簇、環狀簇和新月簇,然后使用k均值聚類分別對其實施聚類操作。結果表明,k均值聚類僅適用于團狀簇,對于環狀簇、新月簇無能為力。聚類的最終效果如下圖所示。
20
基于密度的空間聚類具有更好的適應性,可以發現任何形狀的簇。
基于密度的空間聚類,全稱是基于密度的帶噪聲的空間聚類應用算法(英文簡寫為DBSCAN)。該聚類算法將簇視為被低密度區域分隔的高密度區域,這與K均值聚類假設簇總是凸的這一條件完全不同,因此可以發現任何形狀的簇。
DBSCAN類是Scikit-learn聚類子模塊cluster提供的基于密度的空間聚類算法,該類有兩個重要參數eps和min_samples。要理解DBSCAN 類的參數,需要先理解核心樣本。如果一個樣本的eps距離范圍內存在不少于min_sample個樣本(包括這個樣本),則該樣本稱為核心樣本。可見,參數eps和min_samples 定義了簇的稠密度。
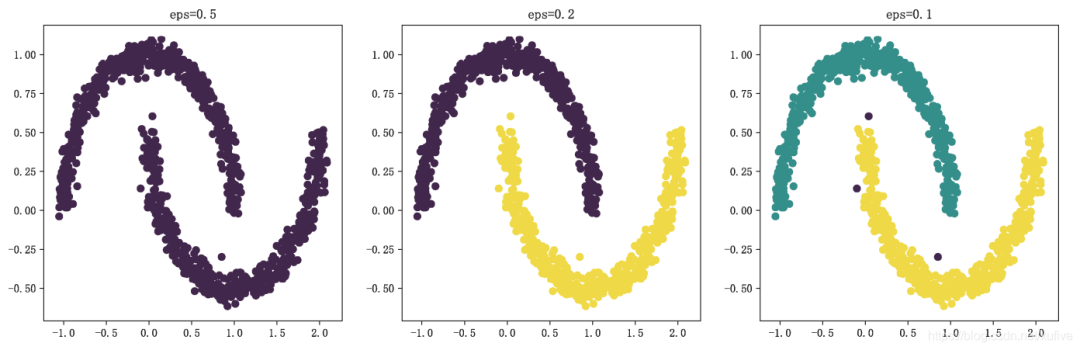
>>> from sklearn import datasets as dss>>> from sklearn.cluster import DBSCAN>>> import matplotlib.pyplot as plt>>> plt.rcParams['font.sans-serif'] = ['FangSong']>>> plt.rcParams['axes.unicode_minus'] = False>>> X, y = dss.make_moons(n_samples=1000, noise=0.05)>>> dbs_1 = DBSCAN() # 默認核心樣本半徑0.5,核心樣本鄰居5個>>> dbs_2 = DBSCAN(eps=0.2) # 核心樣本半徑0.2,核心樣本鄰居5個>>> dbs_3 = DBSCAN(eps=0.1) # 核心樣本半徑0.1,核心樣本鄰居5個>>> dbs_1.fit(X)DBSCAN(algorithm='auto', eps=0.5, leaf_size=30, metric='euclidean', metric_params=None, min_samples=5, n_jobs=None, p=None)>>> dbs_2.fit(X)DBSCAN(algorithm='auto', eps=0.2, leaf_size=30, metric='euclidean', metric_params=None, min_samples=5, n_jobs=None, p=None)>>> dbs_3.fit(X)DBSCAN(algorithm='auto', eps=0.1, leaf_size=30, metric='euclidean', metric_params=None, min_samples=5, n_jobs=None, p=None)>>> plt.subplot(131)0x00000180C4C5D708>>>> plt.title('eps=0.5')Text(0.5, 1.0, 'eps=0.5')>>> plt.scatter(X[:,0], X[:,1], c=dbs_1.labels_)0x00000180C4C46348>>>> plt.subplot(132)0x00000180C4C462C8>>>> plt.title('eps=0.2')Text(0.5, 1.0, 'eps=0.2')>>> plt.scatter(X[:,0], X[:,1], c=dbs_2.labels_)0x00000180C49FC8C8>>>> plt.subplot(133)0x00000180C49FCC08>>>> plt.title('eps=0.1')Text(0.5, 1.0, 'eps=0.1')>>> plt.scatter(X[:,0], X[:,1], c=dbs_3.labels_)0x00000180C49FC4C8>>>>plt.show()
以上代碼使用DBSCAN,配合適當的參數,最終將新月數據集的上弦月和下弦月分開,效果如下圖所示。
21
主成分分析(PCA)是一種統計方法,也是最常用的降維方法。
主成分分析通過正交變換將一組可能存在相關性的變量轉換為一組線性不相關的變量,轉換后的這組變量叫主成分。顯然,主成分分析的降維并不是簡單地丟掉一些特征,而是通過正交變換,把具有相關性的高維變量合并為線性無關的低維變量,從而達到降維的目的。
以下代碼以鳶尾花數據集為例演示了如何使用 PCA 類來實現主成分分析和降維。已知鳶尾花數據集有 4 個特征列,分別是花萼的長度、寬度和花瓣的長度、寬度。
>>> from sklearn import datasets as dss>>> from sklearn.decomposition import PCA>>> ds = dss.load_iris()>>> ds.data.shape # 150個樣本,4個特征維(150, 4)>>> m = PCA() # 使用默認參數實例化PCA類,n_components=None>>> m.fit(ds.data)PCA(copy=True, iterated_power='auto', n_components=None, random_state=None, svd_solver='auto', tol=0.0, whiten=False)>>> m.explained_variance_ # 正交變換后各成分的方差值array([4.22824171, 0.24267075, 0.0782095 , 0.02383509])>>> m.explained_variance_ratio_ # 正交變換后各成分的方差值占總方差值的比例array([0.92461872,0.05306648,0.01710261,0.00521218])
對鳶尾花數據集的主成分分析結果顯示:存在一個明顯的成分,其方差值占總方差值的比例超過92% ;存在一個方差值很小的成分,其方差值占總方差值的比例只有0.52% ;前兩個成分貢獻的方差占比超過97.7%,數據集特征列可以從4個降至2個而不至于損失太多有效信息。
>>> m = PCA(n_components=0.97)>>> m.fit(ds.data)PCA(copy=True, iterated_power='auto', n_components=0.97, random_state=None, svd_solver='auto', tol=0.0, whiten=False)>>> m.explained_variance_array([4.22824171, 0.24267075])>>> m.explained_variance_ratio_array([0.92461872, 0.05306648])>>> d = m.transform(ds.data)>>> d.shape(150,2)
指定參數n_components不小于0.97,即可得到原數據集的降維結果:同樣是150個樣本,但特征列只有2個。若將2個特征列視為平面直角坐標系中的x和y坐標,就可以直觀地畫出全部樣本數據。
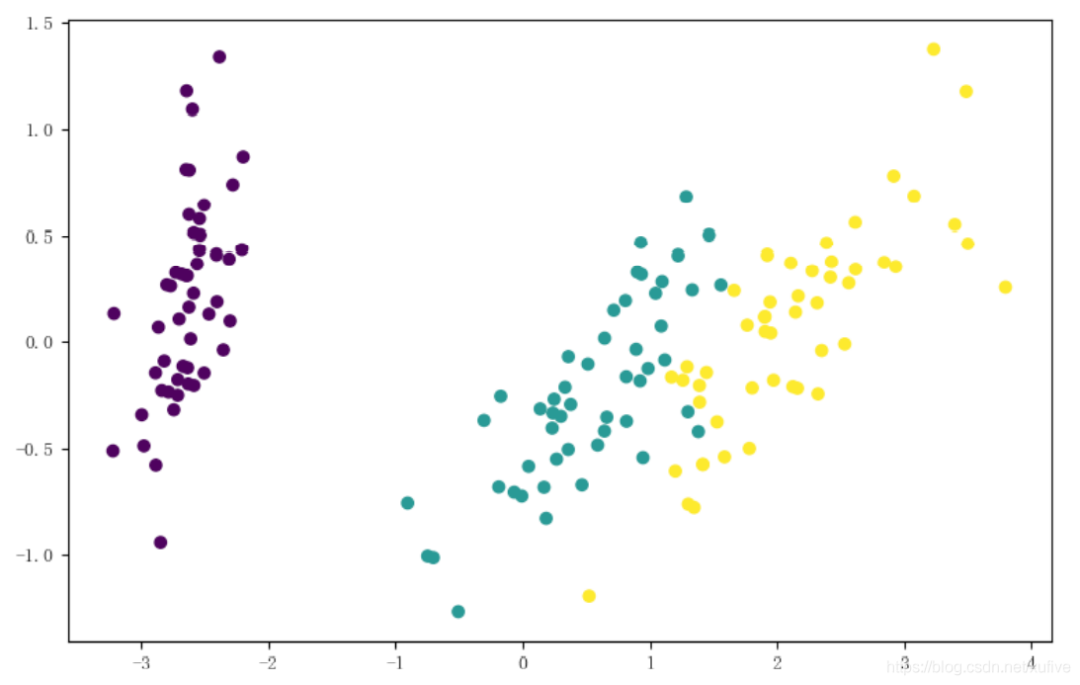
>>> import matplotlib.pyplot as plt>>> plt.scatter(d[:,0], d[:,1], c=ds.target)0x0000016FBF243CC8>>>>plt.show()
下圖顯示只用2個特征維也基本可以分辨出鳶尾花的3種類型。
-
人工智能
+關注
關注
1794文章
47642瀏覽量
239674 -
代碼
+關注
關注
30文章
4823瀏覽量
68902 -
機器學習
+關注
關注
66文章
8438瀏覽量
132930
發布評論請先 登錄
相關推薦
如何選擇云原生機器學習平臺
什么是機器學習?通過機器學習方法能解決哪些問題?

開關電源布線 一句話:要運行最穩定、波形最漂亮、電磁兼容性最好

求助,關于TLE2141的供電問題求解
【「時間序列與機器學習」閱讀體驗】+ 鳥瞰這本書
深度學習與傳統機器學習的對比
一句話讓你理解線程和進程

圖機器學習入門:基本概念介紹

請問AD2428 TX crossbar是個什么功能?
STM32H750配置時ETH中有一句話‘the eth can work only when ram is pointing at 0x24000000’是什么意思?
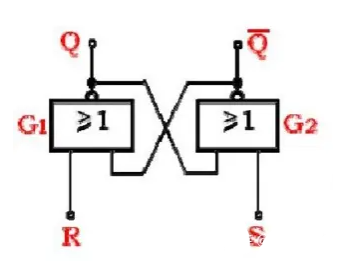
RS觸發器邏輯門組成和邏輯功能表




 21句話入門機器學習
21句話入門機器學習











評論