摘要
密碼是保障網絡通信安全的堡壘,隨著量子計算的出現,經典密碼體制在維護信息安全方面面臨著巨大的挑戰。目前,后量子密碼算法是理論上證明可保障量子環境下通信安全的新型密碼方案。通過分析現有量子計算技術與后量子密碼方案設計的研究進展,強調后量子密碼研究的緊迫感,表明后量子密碼的研究在信息安全中的重要性,最后指出后量子密碼下一步可能的研究方向,為我國后量子密碼技術研究提供參考。
古有飛鴿,現有網絡,在以知識經濟為基礎的信息化社會中,保障網絡信息安全無疑成為國與國之間無形的武器。歷史上,圖靈發明電子計算機破譯了密碼機,打破了國家之間信息安全的屏障。此后在經典計算機上,人們通過設計基于數學上 NP 難問題的加解密算法,維護了近 50 年的網絡信息與通信安全。但是,1982年 Feynman首次提出將量子力學與計算機相結合的構想,開辟了量子時代的新紀元。1985 年Deutsch進一步闡述了量子計算機的基本概念,并證實了在某些方面,量子計算機相比經典計算機而言確實具有更強大的功能。1994 年 Shor給出了一個能夠在多項式時間內解決大整數分解和離散對數問題的 Shor 量子算法。至此,人們察覺到在功能強大的量子計算機面前,現有密碼技術搭成的“城墻”是如此的“不堪一擊”,因此設計研究能夠抵抗量子計攻擊的下一代加密算法也變得迫在眉睫。
1
量子計算機的發展現狀
20 世紀后期,量子計算機作為量子力學與計算機技術相結合的重要成果而備受國際關注。鑒于其具有實際的戰略意義,世界各國都高度重視并不斷加大投入,通過陸續制定各種政策、建立一系列的研究機構、啟動各類項目來支持量子計算機的研究,推動了量子科技研發和技術產業的蓬勃發展。美國政府在此領域率先行動,斥巨資推出了 5 個專門針對量子計算機的研究計劃,分別是由美國國防高級研究計劃局提出的“量子信息科學與技術發展規劃”、由美國國家安全局指導的 ARDA5 計劃、以美國科學基金會為依托的 QuBIC 計劃、由美國宇航局領導部署的 QCTG 計劃以及美國國家標準與技 術 研 究 院(National Institute of Standards and Technology,NIST)指揮的PLQI計劃。除此之外,歐盟、加拿大、中國等組織、國家和地區在量子計算機領域的研究也做出積極響應并取得了一系列的研究成果。
2001 年, 一 個 由 IBM 公司成功研發的 7qubit 的示例性量子計算機成功領跑了該領域的研究。2007 年,中國科學家潘建偉首次在量子計算機上實現了 Shor 量子分解算法 ,該成果標志著中國光學量子計算機的研究在國際上已經達到了先進水平。2008 年,加拿大的 D-wave公司對已有量子計算機系統進行改進并成功將運算位數提高到 48 qubit。2010 年,英國布里斯托爾大學開發出了一種新的光子芯片,該芯片速度更快、存儲量更大,為量子計算機的信息存儲提供了新的思路。同年,潘建偉團隊與清華大學組成的聯合小組通過研究量子隱形傳態技術的特點,成功實現了世界上最遠距離的量子傳輸 并將該研究成果發表在國際權威雜志 Nature Photonics 上,該成果向全球展示了基于量子計算機的量子通信網絡實現的可行性。與此同時,杜江峰教授在 Nature 上發表了一篇關于保持固態自旋比特的量子相干性研究的論文,該成果對固態自旋量子計算機的實現具有重要意義。后來,英國和澳大利亞的聯合研究小組設計了一種稱為 FTQC 的容錯量子計算方案,該方案的提出奠定了量子計算機走向實用化的基礎。
隨著量子計算技術與硬件設備材料的飛速發展,人們愈發堅信量子計算機走向現實欠缺的不再是技術原因,而是時間的沉淀,借此各國加快針對量子計算機的研究腳步。2016 年,中國在“十三五”規劃中明確設立關于“量子通信與量子計算機”的重大科研項目 。同年,Shor 量子分解算法成功運行在潘建偉團隊研究的光量子計算機上,為紀念這一研究成果,發射了國際上第一顆名為“墨子號”的量子衛星。2017 年,潘建偉團隊自主研發的 10 bit 超導量子線路樣品成功實現了當時世界上最大數目的超導量子比特糾纏和完整測量,在量子計算機的發展道路上又邁上了一個新的臺階。2018 年,歐盟正式啟動“量子技術旗艦計劃”,該計劃擬在歐洲建設一個連接所有量子計算機、模擬器與傳感器的量子通信網絡 。2019 年, 谷歌團隊在量子計算原型機“懸鈴木”上僅用了3 分 20 秒就完成了超級計算機一萬年計算量的工作,該成果將量子計算機的處理能力又帶向新的高度,一定意義上實現了量子霸權。2020年,美國白宮網站發布的《美國量子網絡戰略構想》提出,開發一種由量子計算機和其他量子設備組成的量子互聯網的設想,并指出下一步的工作是使量子信息科學全民化。2021 年,中國提出了新的“十四五”規劃,指出這 5 年是中國量子技術實現“彎道超車”的關鍵時期,其目標之一就是研制通用量子計算原型機和實用化量子模擬機 。同年 10 月,潘建偉團隊與其他研究機構合作,成功構建了 113 個光子 144 種模式的量子計算原型機“九章二號”,實現了在高斯玻色取樣數學問題上的快速求解。除此之外,潘建偉團隊及其合作伙伴還成功研制出了66超導量子比特的“祖沖之二號”,相比于“懸鈴木”,在計算復雜度方面提高了 6 個數量級。2022 年,Huggins 等人在 Nature 上發表文章,將 QMC 方法與量子計算相結合,構建了混合量子經典計算模型,提供了一條實現實際量子優勢的途徑,為實用化量子計算機的設計提供了理論基礎。
量子計算機的快速發展減少了高計算量問題的處理時間,解決了大量復雜的數學問題,給當前已經發展成熟并且應用廣泛的現代公鑰密碼體制帶來了巨大的威脅與嚴峻的挑戰。然而,保障量子計算機下網絡安全與信息系統安全的重點在于密碼技術的發展,因此,在量子信息時代來臨之前,設計能夠有效抵御量子計算機攻擊的新型密碼體制就成了密碼學家們不得不面對的問題之一。
2
抵御量子威脅時不我待
2.1抵御量子威脅的戰略意義
密碼技術是維護信息安全的重中之重,大量應用于國家保密系統和大型國防裝備。一旦量子計算機問世,現代密碼學中基于大整數分解、離散對數問題設計的公鑰密碼將被攻破,直接威脅到當前黨政軍民領域的網絡與信息安全,甚至威脅國家安全。
在軍事方面,“先存儲后破譯”是破解當前密碼系統的一個重要戰略,即一些組織將現在無法破譯的信息先存儲起來,等到日后時機成熟再進行破譯,如果按照“摩爾定律”的規律來看,這個成熟的時機很可能在非常長的時間內都不可能來臨,而量子計算的出現,加快了成熟時機的到來,對長期保密性以及前向安全性都造成了致命的威脅。通常,在國家軍隊與許多重要機構的設備中存儲了大量的國家安全情報,這些情報需要保存十幾年甚至更長的時間不能被破解,由此可見,量子計算的出現將直接威脅到國家重要情報的安全,因此必須盡快研制出能夠抵抗量子計算機的新型加密體制,以最大限度地解除該隱患。
在日常通信方面,許多關鍵的通信協議大多以公鑰加密、數字簽名和密鑰交換為依托,然而這些公鑰密碼學算法基于的特定數論難題的困難性在量子計算面前“不值一提”,一旦量子計算機實用化,這些通信協議將紛紛變得不再安全,無法保障端到端的安全傳輸。
2.2密碼算法的實用化需要時間孵化
任何一個密碼算法的設計都是為了最終遷移到工程化。從現代密碼算法理論技術發展成熟到最終的標準化,人們花費了近 20 年的時間才構造出一套完整的公鑰密碼系統基礎設施。即使新型密碼算法的理論技術已經發展成熟,但將現在廣泛應用的密碼系統逐步轉化為能夠抵抗量子計算機攻擊的新型密碼系統也需要大量時間,更何況現在能夠抵抗量子計算機攻擊的新型密碼算法的理論技術還未發展成熟。因此,不管量子時代何時到來,盡快采取行動設計新型密碼方案,保障量子計算機信息與通信系統的安全都十分必要。
3
全球守護量子時代下的信息安全
沿襲經典計算機中設計公鑰密碼算法的思路,目前國際上應對量子計算機攻擊的后量子密 碼(Post-Quantum Cryptography,PQC)算法主要集中在尋找一類或多類在量子計算機上多項式時間內不可解的數學困難問題。根據這些困難問題設計出的 PQC 算法可以在一定程度上抵抗量子計算機的攻擊,守護量子信息時代下的通信安全。全球針對 PQC 算法的研究主要集中在兩個方面:國際學術交流和算法標準化的建立。
3.1后量子密碼理論的國際學術交流
作為密碼學領域的分支,國際 PQC 理論和技術的研究一直以來都受到了各國關注,相關的學術交流活動的數量和頻度逐年遞增,其影響范圍向更多的國家和領域輻射。
2006 年, 國 際 密 碼 研 究 協 會 舉 辦 了 第 一屆后量子密碼技術國際會議,該會議討論了PQC 在未來的研究中可能存在的潛在領域。此后,這項會議分別在北美、歐洲、東亞等多個地區連續舉辦,并通過在相鄰會議間隙舉辦夏季或冬季培訓營的方式,促進了各國研究者之間的交流,增強了 PQC 技術的發展。
2011 年, 美 國 安 全 創 新 公 司 注 冊 并 擁 有NTRU 算法的專利,自此,該公司設計并開發了多種 NTRU 算法實現的軟件庫。2013 年,歐洲電信標準協會與加拿大滑鐵盧大學量子計算中心聯合舉辦了量子安全密碼工作組會議(IQC/ETSI Quantum-Safe Crypto Workshop),參會代表來自密碼學、數學、物理學、計算機等多個不同的研究領域,目標是部署下一代密碼基礎設施,特別是抵御量子計算帶來的沖擊。2015 年 1 月,歐盟啟動 PQC 算法 SAFECRYPTO 應用項目。借助歐洲多所企業、高校和研究機構的力量,相繼開展了 PQCRYPTO 項目 和 PROMETHEUS 項目,并將 PQCRYPTO 項目納入歐盟地平線 2020計劃,致力于打造新一代安全實用的 PQC 方案。2016 年 4 月,微軟公司開發出了基于格上的困難問題 RLWE 的格密碼庫(Lattice Crypto),微軟公司表示攻擊者無論是使用經典計算機還是量子計算機,該軟件庫至少能夠實現 128 位的安全性能。同年 7 月,谷歌公司宣布將開始進行 PQC 技術的測試活動,并表明本次測試對象為基于RLWE問題的密鑰交換協議。2019年1月,谷歌宣布將部署一種稱為組合橢圓曲線和后量子密鑰交換(CECPQ2)的新的傳輸層安全性協議(Transport Layer Security,TLS)密鑰交換方法。同時,谷歌和 Cloudflare 將合作探索 PQC 如何在實踐中擊敗超文本傳輸安全協議(Hypertext Transfer Protocol Secure,HTTPS)連接。2022 年4 月,IBM 公司發布了首個基于格理論研發的量子安全系統——IBMz16。
亞洲密碼學研究者在后量子相關技術的發展中也在積極跟進。2016 年 6 月,首屆亞洲后量 子 密 碼 論 壇(PQCAsia Forum)在我國成都順利召開。鑒于 PQC 算法的飛速發展,原定于2017 年召開的第二屆亞洲后量子密碼論壇提前到 2016 年 11 月于韓國首爾大學召開。2020—2021 年,丁津泰所帶領的團隊先后破解了兩個NIST 抗量子數字簽名候選方案,包括 Luov 和GeMMS,并將研究成果發表在 2020 年“歐洲密碼學年會”和 2021 年“美國密碼學年會”上。2022 年,上海交通大學的谷大武教授領導的LoCCS 實驗室成功破解了 80 維格的容錯學習問題(Learning With Errors,LWE),創造了格密碼中困難問題求解新的世界紀錄,同時該紀錄已經在格密碼挑戰的官方網站 LWE Challenge上進行了公布。
3.2后量子密碼方案的標準化建立
目前,全球已經有眾多國家意識到未來量子攻擊對網絡安全帶來的潛在威脅,也已采取必要行動和相關部署來應對此威脅。類似于現代密碼學中 DES、AES、RSA、ElGamal 等加密算法標準,在 PQC 理論的研究過程中,標準化的建立也逐步發展起來,越來越多的國際參與者紛紛加入 PQC 方案標準化建立的研究中。
3.2.1美國后量子密碼標準化計劃
早 在 2008 年,NTRU 加密算法就已經被美國電氣和電子工程師協會確定為正式標準(Std1363.1—2008)。2010 年,其又被認可標準 委 員 會(Accredited Standards Committee X9)批準為可用于數據防護的新型加密標準。同時,美國國家標準學會 X9.98 標準(ANSIX9.98)明確了在金融交易過程中如何使用基于諸如 NTRU等格加密算法的公私鑰加密系統。
2015 年 8 月,美國國家安全局宣布對當前美國政府所使用的“密碼算法 B 套件”進行安全性升級,升級的算法將用于后量子時代過渡期的加密標準。2016 年 4 月,NIST 頒布“后量子密碼學”研究報告 ,并宣布將啟動 PQC算法標準計劃。截至 2017 年 12 月,NIST 共收到來自全球共 82 份候選密碼方案,自此開啟了后量子密碼學標準協議的第一輪預選。2019年 1 月,NIST 揭曉第二輪的標準方案,本輪共有 26 個密碼方案脫穎而出,其中包括 17 個公鑰加密 / 密鑰交換方案和 9 個數字簽名方案。按照密碼方案的構造方式來看,這 26 個候選算法中包括 12 個格密碼,7 個基于編碼的密碼,4 個基于多變量的密碼,2 個基于哈希的密碼和1 個基于同源曲線的密碼。2021 年 1 月,NIST公布的第三輪候選算法中包括 7 個決賽入選方案和 8 個備選方案,在這 7 個決賽入選方案中,有 5 個都是格密碼,這說明當前格密碼在所有的 PQC 算法中占據較大的優勢,是未來最有望成為標準化的算法。2022 年 3 月,麻省理工學院與阿布扎比技術創新研究所合作編寫并出版了《從今天起,直面明天的量子黑客》(Facing Tomorrow’s Quantum Hackers Today)。該報告對全球量子計算公司中的密碼學家、數學家、物理學家和高級管理人員進行采訪,評估了一臺成熟的量子黑客計算機對如今網絡安全系統的威脅與影響,并在此基礎上分析了應對威脅的解決方案,這意味著 NIST 標準化即將進入第四輪。2022 年 7 月,NIST 已完成第三輪 PQC 標準化過程,共有 4 個候選算法被選中標準化,分別是 CRYSTALS-KYBER、CRYSTALS-Dilithium、FALCON 和 SPHINCS+,另外還有 4 種算法將繼續進入第四輪,這一里程碑事件意味著持續6 年的標準化工作終于進入了最后階段。
3.2.2歐洲后量子密碼標準化計劃
首先,在 NIST-PQC 算法的征集過程中,歐洲研究團隊做出了重大的貢獻,在 NIST 發布的第二輪 26 個標準方案中,歐洲主導和參與的高達 20 多個。其次,歐洲量子密碼學術和工業界研究者聯合組織的 PQCrypto 項目于 2015 年發布了一份初始報告,該報告在加密算法、對稱授權以及簽名系統等多個領域都提出了相關的標準化建議,并指出 McEliece 密碼系統具有發展成為替代 RSA/ECC 密碼系統的潛力。此外,歐洲電信標準協會 ETSI 成立的“量子安全密碼工業標準工作組”主要負責 PQC 算法的征集、評估以及工業標準的制定,該組織每年發布一本“量子安全白皮書”,用以公布后量子密碼研究的最新進展。
3.2.3日本后量子密碼標準化計劃
為應對量子計算攻擊和對加密設備的物理攻擊(例如功率分析),日本推出了 CREST 密碼數學項目,旨在為下一代加密系統的開發奠定基礎。CREST 項目每年舉辦的后量子安全的相關會議,為日本后量子密碼學研究者交流重要成果提供了平臺。在真正的 PQC 標準公布之前,日本密碼研究與評估委員會列出了 3 個密碼清單:電子政務推薦密碼清單、候選推薦密碼清單和監控密碼清單,并指出將啟動最新制定的 PQC 指南。
3.2.4韓國后量子密碼標準化計劃
為及時跟進國際后量子標準化工作,韓國于 2022 年推出了全球首個可防御量子計算機黑客攻擊的 PQC 專線,目前,該線路已經過電信技術協會的測試和驗證。
3.2.5中國后量子密碼標準化計劃
雖然中國在PQC標準化的研究中起步較晚,但在 NIST-PQC 算法征集活動中也參與并貢獻了一定的力量。參與設計的中國團隊包括密碼科學技術國家重點實驗室、上海交通大學、復旦大學、中科院信工所以及中國臺灣地區“中央研究院”等。其中,由中國科學院數據與通信保護研究教育中心設計的 LAC 算法,與歐洲、美國、加拿大等國家提供的 PQC 算法一起,入選了 NIST 第二輪 PQC 密碼算法名單。除此之外,中國在國內 PQC 算法標準的征集活動中也做了一些工作。自 2019 年起,中國密碼學會(Chinese Association for Cryptologic Research,CACR)開始舉辦全國密碼算法設計競賽 ,該競賽僅面向中國的密碼學者,受到了廣大密碼學家的青睞,并在公鑰密碼組的參賽作品中征集到大量的 PQC 算法。該競賽的成功舉辦推動了我國密碼理論與應用技術的發展,是我國在 PQC 算法標準制定過程中的基礎,意味著我國 PQC 技術的研究正逐步向國際先進水平看齊,致力于通過充分調動國內各界研究力量,推動國產化研發,保障未來后量子時代下我國的網絡空間安全。
綜上所述,從世界各國政府對該領域的投入與支持力度來看,在真正的量子信息時代到來之前,全球的目標均是在量子通信網絡中實現保密通信與安全認證。
4
后量子密碼的構造方式
在 PQC 算 法 的 設 計 方 案 中, 大 多 還 是 基于數學困難問題的難解性,目前主流數學困難問題主要包括格、編碼、哈希以及多變量。除此之外,基于超奇異橢圓曲線、量子隨機漫步等技術的 PQC 構造方法以及較大密鑰長度的對稱密碼算法也被認為是量子計算機條件下相對安全的。
4.1基于格的后量子密碼算法
格(lattice)是一種數學結構,定義為一組線性無關的非零向量(稱作格基)的整系數線性組合。具體來說,給定一組格基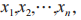 對任意的整數
對任意的整數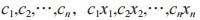 都是屬于這個格的向量,其中 n 稱為格的維數。對于同一個格,其可以擁有不同的格基,并且求解格中的最短向量問題(Shortest Vector Problem,SVP)和最近向量問題(Closest Vector Problem,CVP)是目前格理論中主要的非確定性多項式難題(Nondeterministic Polynomially problem,NP)。除此之外,格中還有一些其他的困難問題,比如 LWE 問題、有界距離解碼問題、小整數解問題、gap-SVP 問題等,因此,基于格的 PQC 算法大多依托這些困難問題而設計,但其本質上又都可以轉化為 SVP 困難問題和 CVP 困難問題。基于格的算法與現代公鑰加密算法的功能一樣,均可實現加解密、數字簽名、屬性加密、同態加密、密鑰交換等多種密碼學構造。
都是屬于這個格的向量,其中 n 稱為格的維數。對于同一個格,其可以擁有不同的格基,并且求解格中的最短向量問題(Shortest Vector Problem,SVP)和最近向量問題(Closest Vector Problem,CVP)是目前格理論中主要的非確定性多項式難題(Nondeterministic Polynomially problem,NP)。除此之外,格中還有一些其他的困難問題,比如 LWE 問題、有界距離解碼問題、小整數解問題、gap-SVP 問題等,因此,基于格的 PQC 算法大多依托這些困難問題而設計,但其本質上又都可以轉化為 SVP 困難問題和 CVP 困難問題。基于格的算法與現代公鑰加密算法的功能一樣,均可實現加解密、數字簽名、屬性加密、同態加密、密鑰交換等多種密碼學構造。
第一個基于格的密碼方案是 1997 年由 Ajtai等人提出的 Ajtai-Dwork 密碼體制,該方案利用格問題中 Worst-case 到 Average-case 的規約來抵抗量子計算的攻擊。第一個基于格的實用的密碼方案是 1998 年由 Hoffstein 等人提出的 NTRU 公鑰加密體制,該方案堅持到了 NIST第三輪的候選算法中,并且目前已經應用在某些商用的密碼設備中,有望日后代替 RSA 加密算法。
在后量子加解密算法方面,通過總結目前主流的基于格的加解密算法,我們發現以 LWE困難問題為基礎的格密碼方案不僅應用廣泛,而 且 安 全 性 更 高。以 NIST 第四輪入選算法CRYSTALS-Kyber 為例,該算法基于的困難問題是 M-LWE 問題,即 LWE 問題與 R-LWE 問題的組合,該問題相比于 LWE 問題而言具有易于擴展和效率高的優點。M-LWE 問題的主要思想是對于在多項式環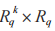 中均勻隨機選取的
中均勻隨機選取的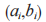 與經過公式
與經過公式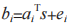 計算得到的
計算得到的 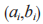 是不可區分的,其中
是不可區分的,其中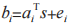 中
中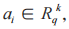 s 和
s 和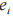 是從二項分布
是從二項分布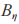 中隨機均勻選取的,該問題的主要困難性在于根據已知
中隨機均勻選取的,該問題的主要困難性在于根據已知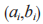 無法計算 s 和
無法計算 s 和 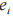 中的任意一個。Kyber 算法就是利用此原理,通過公式
中的任意一個。Kyber 算法就是利用此原理,通過公式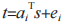 生成公私鑰對 (t,s),達到已知公鑰 t 后無法計算私鑰 s 的效果,此后再對通信的明文信息進行加密或者對通信雙方的臨時會話密鑰進行封裝。以 2020 年提交的第三版 Kyber算法為例,表 1 闡述了選擇明文攻擊下的不可區分性(IND-CPA)安全的 Kyber 算法的具體實現思路,表 2 闡述了自適應選擇密文攻擊下的密文不可識別性(IND-CCA2)安全的 Kyber 算法的具體實現思路。
生成公私鑰對 (t,s),達到已知公鑰 t 后無法計算私鑰 s 的效果,此后再對通信的明文信息進行加密或者對通信雙方的臨時會話密鑰進行封裝。以 2020 年提交的第三版 Kyber算法為例,表 1 闡述了選擇明文攻擊下的不可區分性(IND-CPA)安全的 Kyber 算法的具體實現思路,表 2 闡述了自適應選擇密文攻擊下的密文不可識別性(IND-CCA2)安全的 Kyber 算法的具體實現思路。
表 1 Kyber 算法實現過程(IND-CPA 安全)

表 2 Kyber 算法實現過程(IND-CCA2 安全)

在后量子簽名算法方面,基于格的簽名算法的構造與現有的公鑰密碼體制略有不同。對于 RSA、ElGamal、橢圓曲線等現有公鑰密碼體制而言,通過調換加解密算法的公私鑰順序即可將其轉換為簽名算法;但是基于格的密碼方案不具有此種對偶特性,在設計基于格的后量子簽名算法時通常采用零知識證明協議進行構造,即證明者證明自己擁有與對應身份的公鑰相匹配的私鑰,但是不泄露任何關于私鑰的信息。
2008 年,Gentry 等人提出了 GPV 框架,該框架指出了基于格的簽名算法的設計思路,如表 3 所示。
表3GPV 框架

以 GPV 框架為基礎,基于格的簽名算法在進行公私鑰對生成的過程中底層基于的困難問題與后量子加解密算法類似,即 LWE 問題和SIS 問題,同時為了便于簽名算法的實現,設計方案時大多借助 NTRU 格實例化 GPV 框架,并通過采樣完成數字簽名的創建,比如進入 NIST第 四 輪 的 簽 名 算 法:FALCON 算 法。除 此 之外,另一個比較受歡迎的簽名算法 CRYSTALSDilithium 也進入了 NIST 的第四輪中。
在具體的設計過程中,CRYSTALS-Dilithium和 FALCON 兩個算法針對算法本身的安全性和算法的運行速度分別進行了不同的改進。其中 CRYSTALS-Dilithium 簽名算法在設計時采用Fiat-Shamir with Aborts 技術,該技術使用拒絕采樣的方式將基于格的 Fiat-Shamir 方案變得更加緊湊且安全;由于傳統的簽名算法中高斯采樣難以高效且安全地實現,Dilithium 簽名算法改進了采樣方式,僅通過均勻分布采樣就完成了簽名的創建;同時為減小公鑰的大小,Dilithium簽名算法采用分離高低階位的新技術將其縮小了兩倍以上。對于 FALCON 簽名算法,通過在采樣過程中應用快速傅里葉采樣技術,并在算法內部使用真正的高斯采樣器,由此保證了在無限簽名情況下 FALCON 算法的安全性,即密鑰信息的泄露可忽略不計;同時由于快速傅里葉采樣在實現過程中具有速度快的優勢,使得FALCON 算法在普通計算機上每秒可以生成數千個有效的簽名,并且驗簽過程相比其他簽名算法而言快將近 5~10 倍。關于 Dilithium 和 FALCON簽名算法的具體過程分別如表 4 和表 5 所示。
表 4Dilithium 簽名算法的實現過程
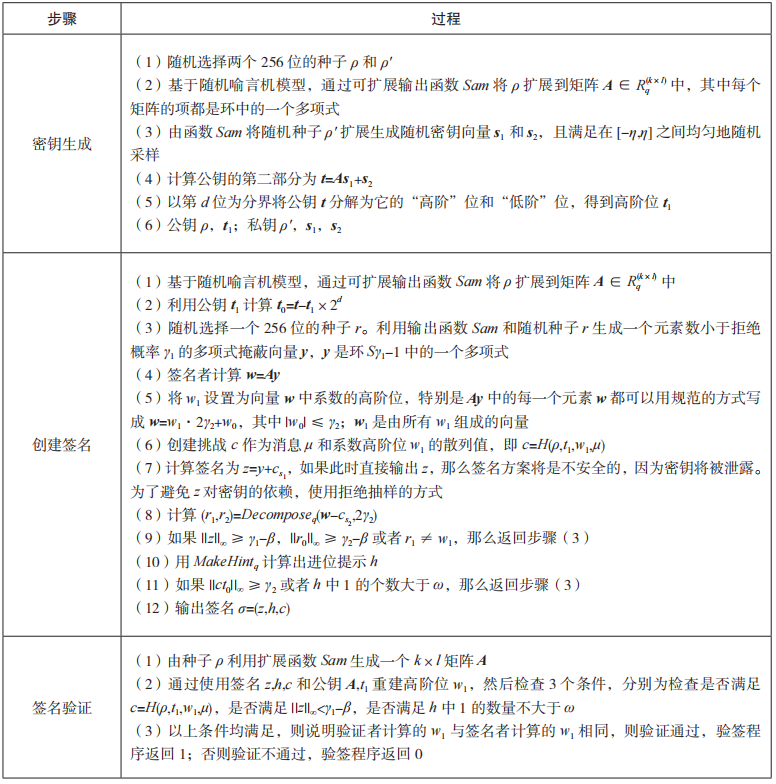
表 5FALCON 簽名算法的實現過程

格密碼的研究雖然起步較晚,但是其簡單的結構以及眾多高復雜度的數學困難問題使其在后量子時代廣受各國學者的歡迎。自 2013 年起,格密碼的研究成果顯著增加,在基于格的密碼體制不斷改進的過程中,密鑰尺寸不斷縮小、運算速度不斷提高,逐步在安全性、密鑰尺寸以及計算速度上達到更好的平衡。2022 年7 月入選 NIST 第四輪的后量子密碼中有 3 個基于格設計的密碼方案,由此足以見得盡管格密碼仍處于發展階段,但目前其已經被認為是最有前景的后量子密碼算法之一。
4.2基于編碼的后量子密碼算法
編碼理論是數學與計算機科學的一個分支,用來處理在噪聲信道中傳送信息時進行錯誤處理。基于編碼的密碼體制也被認為是在量子計算機中相對安全的密碼算法,其核心在于將一定數量的錯誤碼字引入編碼中,糾正錯誤碼字或計算校驗矩陣的伴隨式是困難的。
一個較早提出且至今使用的基于編碼的加密算法是 1978 年 McEliece[27] 提出的 ClassicalMcEliece 公鑰加密方案,該方案使用隨機二進制不可約的 Goppa 碼作為私鑰,記作 A,對私鑰 A使用可逆矩陣 S 和隨機置換矩陣 P 進行 A'=SAP變換后得到的一般線性碼A'作為公鑰的一部分。最終 McEliece 公鑰加密方案的公鑰由 Goppa 碼的漢明重量 t 和矩陣 A' 組成,私鑰由生成矩陣A、可逆矩陣 S 和隨機置換矩陣 P 組成(方案的整體流程如表 6 所示)。該方案基于的困難問題是對稱群隱藏子群問題,也就是在加密過程中對明文信息 x 進行的 y=y'+e=x×A'+e 操作中,從加入混淆 e(帶有 t 個錯誤的向量)的矩陣 A'中反推 Goppa 碼是困難的。該算法相對于現有公鑰密碼體制而言加密速度快,但是由于其公鑰尺寸過大,該算法并不是很實用化,不過針對該算法的改進最終也進入到了 NIST 第三輪的候選算法中。
表 6 McEliece 公鑰加密方案過程

此后,1986 年 Niederreiter 提出了一種基于GRS 碼的背包型公鑰密碼體制——Niederreiter密碼算法,該算法與 McEliece 不同的地方在于在密鑰生成過程中,當確定私鑰 A(生成矩陣)后,借助可逆矩陣 M 和置換矩陣 P 通過 A'=MHP操作來隱藏校驗矩陣 H 而非生成矩陣 A,從而生成算法的公鑰 A'。為證明 Niederreiter 密碼算法的安全性,1994 年,王新梅等人 證明其在安全性方面與 McEliece 是等價的。
針對基于編碼的數字簽名方案而言,王新梅于 1990 年提出了第一個基于編碼的 Xinmei數字簽名方案。次年,李興元構造了一類同時具有簽名、加密和糾錯能力的公鑰體制。隨后,學者們在此基礎上進行了一系列的改進,并指出基于編碼的公鑰密碼體制或許可以成為基于數論的公鑰密碼體制的一個很好的替代。
4.3基于哈希的后量子密碼算法
基于 Hash 函數設計的后量子密碼算法主要集中在數字簽名算法中,Hash 函數具有一個很好的性質就是抗碰撞性,當 Hash 函數能抗強碰撞時,設計的數字簽名算法便可有效抵抗量子計算的攻擊。在基于 Hash 函數的數字簽名算法中,具有代表性的是 1989 年 Merkle 從一次性簽名方案出發,借鑒 Lamport 和 Diffie 的工作,發明的 Merkle 數字簽名方案(MSS)。MSS 的基本思想是利用 Hash 樹將多個一次性驗證密鑰(Hash樹的葉子)的有效性降低到一個公鑰(Hash樹的根)的有效性。由于其良好的抗強碰撞性,使得其可以有效抵抗量子計算的攻擊,因此,MSS 受到了學者們的青睞。從 2006 年舉辦的第一屆國際后量子密碼會議開始,就不斷有人提出針對 MSS 的改進,例如 2006 年,Michael Szydlo提出了一種使 Merkle 樹的構建更加有效和實用的方法;2008 年,基于 Szydlo’s 算法,JohannesBuchmann 等人提供了一種計算數字簽名機制中認證路徑的新方法,并大大減少了最壞情況下算法的運行時間;2011 年,Buchmann 等人 在 MSS 的基礎上提出了一種具有更小簽名的可證明安全的 XMSS 數字簽名方案。
在 MSS 的 研 究 之 外,2016 年,Targhi 等人估計出了尋找一個函數碰撞的量子查詢復雜度。2017 年,SPHINCS+ 算法被提交到 NIST PQC 競賽中,經過層層篩選,該算法進入到了NIST 第三輪候選算法中,后續通過進一步的安全性分析,該算法在 NIST 第四輪評估中脫穎而出,成為正式候選的簽名算法之一。SPHINCS+簽名算法采用了一種被稱為 SPHINCS 超樹的結構進行構造,SPHINCS 超樹是一種在 Merkle 樹和 Goldreich 樹之間相折中的結構,其外層結構是一個 k 叉樹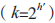 ,一共有 d 層;k 叉樹的每個節點是一個高度為 h' 的 Merkle 樹,Merkle樹的每個子節點是一個密鑰,其中葉子節點用來給外層結構的子節點生成公鑰,非葉子節點用來給 FORS 密鑰生成公鑰;外層結構的葉子結點也是 Merkle 樹, 用 來 給 消 息 進 行 簽 名。SPHINCS+ 簽名算法通過一個偽隨機數生成器和一個隨機種子構造一個 SPHINCS 超樹,然后根據 SPHINCS 超樹生成公私鑰對。在進行消息簽名時,首先計算消息 m 的哈希值 H(m),然后取出 H(m) 的 h 個比特用來確定使用哪一個 FORS密鑰,再取出 kα 個比特用于 FORS 簽名,最終將 SPHINCS 超樹從葉子節點到根節點連在一起的簽名鏈作為消息 m 的簽名。在進行簽名驗證時,接收者依次驗證簽名鏈上的每個簽名即可。
,一共有 d 層;k 叉樹的每個節點是一個高度為 h' 的 Merkle 樹,Merkle樹的每個子節點是一個密鑰,其中葉子節點用來給外層結構的子節點生成公鑰,非葉子節點用來給 FORS 密鑰生成公鑰;外層結構的葉子結點也是 Merkle 樹, 用 來 給 消 息 進 行 簽 名。SPHINCS+ 簽名算法通過一個偽隨機數生成器和一個隨機種子構造一個 SPHINCS 超樹,然后根據 SPHINCS 超樹生成公私鑰對。在進行消息簽名時,首先計算消息 m 的哈希值 H(m),然后取出 H(m) 的 h 個比特用來確定使用哪一個 FORS密鑰,再取出 kα 個比特用于 FORS 簽名,最終將 SPHINCS 超樹從葉子節點到根節點連在一起的簽名鏈作為消息 m 的簽名。在進行簽名驗證時,接收者依次驗證簽名鏈上的每個簽名即可。
盡管目前基于 Hash 函數的數字簽名方案成果并不多,但是考慮 Hash 函數獨特的屬性及其實用性,在量子時代,基于 Hash 函數的簽名算法有望成為最有前途的數字簽名方案之一。
4.4基于多變量的后量子密碼算法
作為后量子密碼算法的最早成員之一,基于多變量的后量子密碼算法相比其他 3 種主流構造方式而言具有更多的研究成果。一個基于多變量的公鑰密碼系統將有限域上一組二次多項式作為它的公鑰映射,其主要安全假設為求解有限域上非線性方程組這個 NP 難問題。
最早的多變量公鑰密碼體制由 Matsumoto 等人 于 1988 年提出,在隨后的 20 多年時間里,諸如清華大學丘成桐數學科學中心的丁津泰、日本的 Kohtaro Tadaki 和我國臺灣地區的 Bo-Yin Yang 等很多知名學者在多變量公鑰密碼領域展開激烈討論并取得了不錯的研究成果。2010 年以來,學者們針對多變量公鑰密碼體制的研究主要集中在 3 個方面:對包括加密、簽名等方案中基本理論的深入研究與改進優化,對類似全同態加密(Fully Homomorphic Encryption,FHE)等熱點領域的重點攻關,對全新算法設計結構的嘗試與探索。據統計,自 2006 年起,在全八屆國際后量子密碼會議收集的論文中,有 39%的論文是針對多變量密碼算法的設計與改進[36],遠遠高于基于其他方式設計的后量子密碼算法,由此可見多變量公鑰密碼體制在后量子時代的地位和意義。
在 眾 多 的 多 變 量 公 鑰 密 碼 體 制 中, 進 入NIST 第三輪的多變量簽名算法就是由丁津泰教授于 2005 年設計的 Rainbow 數字簽名算法。該算法由于采用相對小的有限域以及基礎的邏輯運算而具有較高的運算速度,同時該算法相較于其他簽名算法而言因其較短的簽名長度而更為實用。該算法采用非平衡油醋(Unbalanced Oil and Vinegar,UOV)體制創建簽名,核心是一個多層的 UOV 結構的中心映射。UOV 體制是油 醋(Oil and Vinegar,OV) 體 制 的 擴 展,OV體制在簽名過程中隨機選取一組醋變量代入油醋多項式中,然后結合簽名消息 m 求解一個關于油變量的線性方程組,而 UOV 體制是一種多層的油醋體制,即每一層都是油醋多項式,而且上一層的所有變量是下一層的醋變量。Rainbow數字簽名算法的具體流程如表 7 所示。
表 7 Rainbow 數字簽名算法的實現過程
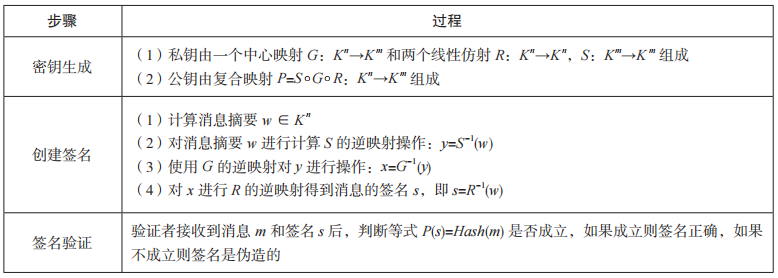
Rainbow 簽名算法自 1999 年起一直經受各種密碼分析,例如 MinRank 攻擊,HighRank 攻擊,Billet-Gilbert 攻擊等 。直到 2022 年,Beullens再次對 Rainbow 簽名算法進行了進一步的改進,并表明對于給定的 NIST 第二輪提交的 SL 1 參數集的公鑰,通過密鑰恢復攻擊,在標準筆記本電腦上平均 53 小時即可返回相應的密鑰。
盡管在 NIST 第四輪的標準化候選算法中沒有多變量公鑰密碼體制,但是在某些注重算法效率的應用場景中,多變量公鑰密碼體制或許會進入一個新的高度。
4.5其他后量子密碼算法
除上述 4 種主流算法外,基于量子密碼和基于同源的密碼體制也在密碼學家的研究范圍內。2012 年,Kashefi 等 人提出了量子單向函數的候選方案,Mosca 等人研究了經典認證密鑰交換框架下量子密鑰的分配問題。2006年,Couveignes介紹了困難的同質空間(Hard Homogeneous Spaces,HHS)的概念并延伸介紹了相關理論,為基于橢圓曲線同源的密碼系統奠定了基礎。同年,Rostovtsev 等人 提出了一個新的適用于公鑰密碼系統的通用數學問題:對于有限域上的橢圓曲線,計算給定橢圓曲線之間的同源(代數同態),與此同時,ElGamal公鑰加密和 Diffie-Hellman 密鑰協議被提出用于同源密碼系統。2014 年,Jao 等人 公布了一個在橢圓曲線同源基礎上不可否認的數字簽名方案。2017 年,Gélin 等人 和 Ti分別對超奇異同源密碼系統的循環終止故障攻擊和第一類 故 障 攻 擊 進 行 了 討 論。2022 年,Castryck、Maino 和 Chi-Domínguez 針對超奇異同源密鑰交換協議(SIDH),分別提出了不同的密鑰恢復攻擊方案。盡管這些后量子密碼算法并未像其他主流算法一樣形成體系,但是在不久的將來,這些后量子密碼算法或者其他新的后量子算法也會逐步登上舞臺。
5
后量子密碼的發展趨勢
量子計算機的出現可以看成新一代的技術革命,作為計算機下一輪迭代的發展方向,量子計算機在密碼破解、機器學習、量子模擬等多個領域具有得天獨厚的優勢,日后量子計算機也極有可能成為人們日常生活中的一部分。后量子密碼算法作為應對量子計算攻擊的新型密碼方案,研究時間不過短短 30 年左右,仍有許多問題亟須探索。
5.1經典后量子密碼算法的優化與拓展
量子計算的發展對密碼技術提出了更高的要求,同時也促成了密碼分析技術的進步。盡管目前已經設計研究出眾多類型的后量子密碼算法,但是針對這些密碼算法的理論攻擊仍然存在,例如面向 NIST 第三輪入選算法中 Kyber 的密鑰不匹配攻擊等,因此在未來對已有的后量子密碼算法的改進之路仍需繼續前行。除此之外,針對算法的實用化改進同樣具有重要意義。通過不斷優化算法的參數設計,提高算法的運行效率,降低算法的時間復雜度和空間復雜度,使算法在實際應用中發揮作用。
5.2量子算法與密碼算法的結合
量子算法的設計目標是解決某一類特定的問題或者縮短某些算法的運行時間,例如 Shor算法的發明解決了大整數分解問題,Grover 算法的提出提高了搜索的速度,Simon 算法的出現提供了一種求解函數周期的方法。研究量子算法與密碼算法相結合的新型算法,一方面,將量子算法應用于后量子密碼的設計中可以提高算法的運行效率,增強其可用性;另一方面,將量子算法應用于密碼分析方法中可以從某個角度發現算法潛在的攻擊可能性,優化算法參數,提高算法的安全性。
5.3密碼算法量子安全性的評估
量子計算中的一些算法已經被證實對經典密碼算法存在有效的理論攻擊,這種攻擊針對后量子密碼算法而言是否有效目前還未知。同時,新的量子算法的出現是否會對現有后量子算法造成威脅也同樣未知,因此評估密碼算法的量子安全性是未來的一個研究方向。
5.4量子環境下新的數學問題探索
除了目前基于格、哈希、多變量、編碼的后量子密碼算法,研究設計更多的基于同源曲線或者量子隨機漫步的后量子密碼算法也是很有必要的。除此之外,研究設計在量子計算機優勢外的數學困難問題也是一種新的探索方向。
6
結語
針對量子計算的發展,美國已經在實施龐大的量子計劃,并公開宣布當項目進行到一定程度后便不再向全球公開,意味著我們將無從獲知其他各國最新的研究進展,這將在一定程度上影響我國的戰略決策。同時,根據量子計算對網絡空間安全方面帶來的威脅,全球目標統一在抗量子密碼的研究上,但是國與國之間還存在一定差距,此后,我國應延續在量子計算、抗量子密碼領域的科研計劃,縮小與西方的差距,切實保障國家的網絡與信息安全。
-
量子計算機
+關注
關注
4文章
535瀏覽量
26058 -
量子算法
+關注
關注
0文章
11瀏覽量
2399
原文標題:后量子密碼的發展趨勢研究
文章出處:【微信號:CloudBrain-TT,微信公眾號:云腦智庫】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦



















評論