2,可信度預測
講解卡爾曼濾波之前,先講一個故事。兩個釀酒師傅判斷當前酒的度,一個老師傅,一個學徒。酒廠里酒的度數,老師傅的判斷大多時候是更加準確,而學徒大多時候的判斷誤差會大一些。一壇經過10天發酵的酒,老師傅說是30度,學徒說是26度。但是這壇酒的實際度數是不知道的,那么我們怎樣知道一個相對準確的結果呢?我們可以直接認為老師傅的回答正確,但是 老師傅也會馬失前蹄,學徒也會有準的時候 ,只是大多數時候誤差大一些。怎么得到相對可信度更高的結果呢。可以通過如下公式:
預測度數=K* 師傅預測+(1-K) * 學徒預測
來作為酒的度數, K可以理解為對老師傅判斷的可信度,1-K可以認為是對學徒判斷的可信度 。顯然讓K大一些,比如K=0.8,說明我們更相信師傅的判斷。隨著學徒技藝的熟練K變為了0.6,那么那么對學徒判斷的權重增加了,對師傅判斷的可信度權重減小了。所以這個K很重要。
同樣的,從工程試驗中來說明,假設有兩個廠商的加速度傳感器A和B,汽車在跑,不斷的讀取A和B,每次會得到兩個值,那么該相信哪個傳感器的結果呢?傳感器測量出來的結果一定是有誤差的,不同廠商的傳感器誤差范圍不一樣,加上傳感器受到的環境的干擾等因素這樣也會干擾傳感器的測量結果。那么怎么得到更加可靠的結果呢?是不是和剛才的師傅判斷酒的度數很像?
假設A廠商的傳感器質量好精度高,B廠商的誤差大,精度小,那么我們肯定更加相信A的測量結果。我們同樣  ,傳感器A
,傳感器A  ,傳感器B
,傳感器B  ,則:
,則:

綜合考慮傳感器A和傳感器B這就是兼聽則明。K越大說明越相信傳感器A測量的數據 。
如何選擇最優的K,使上面得到的 可信度最高呢?這就需要卡爾曼濾波 。
3,卡爾曼濾波
下面這段是百度出來的卡爾曼濾波:
卡爾曼濾波(Kalman filtering)是一種利用線性系統狀態方程,通過系統輸入輸出觀測數據,對系統狀態進行最優估計的算法 。由于觀測數據中包括系統中的噪聲和干擾的影響,所以最優估計也可看作是濾波過程。
用土話來解釋就是測量系統的狀態,由于有各種噪聲,會導致測量結果存在一定的誤差,那么如何降低這些誤差得到更加可信的數據呢,那么就是使用卡爾曼濾波做最優估計。
卡爾曼濾波適用于線性系統,并且系統的噪聲滿足高斯分布 (通常的工程過程噪聲都滿足)。
卡爾曼濾波是 以最小均方誤差為估計的最佳準則 。也就是卡爾曼濾波定義的系統的最優是讓估計結果的分布的方差最小的估計。
接下來引入卡爾曼濾波,首先引入 高斯分布或者叫正態分布 。
通常工業場景中許多測量和過程中的誤差都都滿足正態分布,所以傳感器的測量結果X=T+a,噪聲a滿足高斯分布,所以X也滿足高斯分布。
傳感器的測量結果X滿足高斯分布:

其中期望值是u,方差是****sigma(這個符號打不出來,就是上面分布中的值,后面都用sigma)
數學表達為:
坐標圖為:

高斯分布
然后解釋卡爾曼濾波,還是以剛才的傳感器來說明,日常中各種噪聲,干擾都符合高斯分布。所以傳感器的測量結果也是符合高斯分布
傳感器A的測量 符合:
傳感器B的測量 符合:
其中a和b就是測量噪聲
預測加速度是: 。 概率論可以證明兩個高斯分布的線性組合也符合高斯分布 :
。 概率論可以證明兩個高斯分布的線性組合也符合高斯分布 :

所以預測 符合: 。當K取不同值的時候得到的 u‘和sigma 也不同。那么 最優估計是什么呢?剛才說了是讓方差最小。也就是當取某個K的時候 sigma'最小的估計是最優估計 。
。當K取不同值的時候得到的 u‘和sigma 也不同。那么 最優估計是什么呢?剛才說了是讓方差最小。也就是當取某個K的時候 sigma'最小的估計是最優估計 。

這是一個拋物線,可以證明當  的時候,
的時候,
sigma'取最小值。將K帶入可以得到:

的時候 預測加速度X’也符合高斯分布,并且sigma' 取最小值。這個時候是最優估計,可信度最高。
這就是卡爾曼濾波,我們畫圖如下:

卡爾曼濾波分布
可以看到 預測加速度X’ 更加的瘦高,所以這樣得到的估計更加的可信 。
-
傳感器
+關注
關注
2552文章
51233瀏覽量
754729 -
卡爾曼濾波
+關注
關注
3文章
166瀏覽量
24660 -
高斯分布
+關注
關注
0文章
6瀏覽量
2764
發布評論請先 登錄
相關推薦




 卡爾曼濾波算法介紹
卡爾曼濾波算法介紹

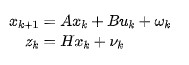










評論