我們認識了音頻濾波器,講解了音頻濾波器同時具有相位調制的功能。但前文中我們略過了濾波器最重要的功能:移除頻譜中的一部分諧波從而創造新的聲音。但濾波器的工作方式可遠沒有聽起來簡單,本文我們將繼續深入了解濾波器的原理。
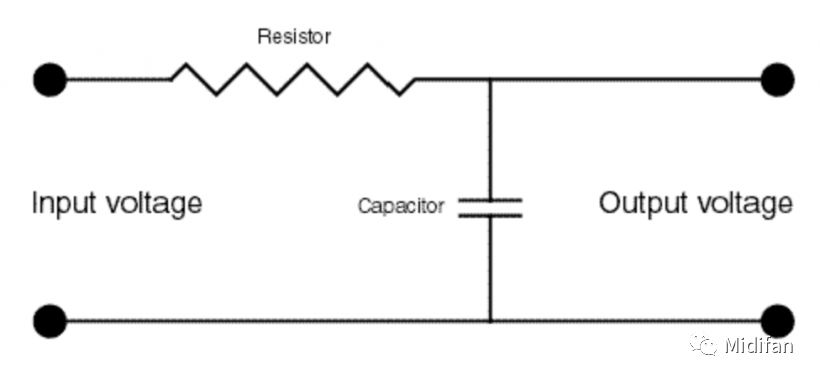
圖 1:一個簡單的低通濾波器電路
圖 1 展示的是我們在上一篇文章中介紹的被動低通 RC 濾波器(之所以稱它為「被動」是因為我們將只需要輸入信號,不需要額外供電的電子元器件稱之為「被動元件」,因此電阻器、電容器以及電感器均為被動元件,而晶體管以及其他放大器則不是被動元件)。如果你有閱讀上一篇文章,那么你可能還記得 RC 濾波器的截止頻率可以通過其電路中的兩個被動元件的容量決定。
輸入進濾波器的信號與經過濾波器處理的輸出信號之間的關系叫做傳遞函數。準確來說,傳遞函數描述的是濾波器的振幅相應(濾波器對音量的影響)以及相位響應,但由于我們已經在上一篇文章中討論了濾波器對音頻相位的影響,本文中我們只將關注振幅相應。理想狀態下,我們的 RC 濾波器的傳遞函數非常簡單:每高于截止頻率(本文中記作 Fc)的兩倍,信號的輸出就將會減半(見圖 2)。

圖 2:RC 低通濾波器在理想狀態下的響應圖示
所以,打比方說 Fc 為 1kHz,那么信號在 2kHz 位置處的增益為 1/2(也就是說一半的音量),4kHz 的位置輸出增益為 1/4(四分之一音量),以此類推...由于頻率每翻一倍音高就上升一個八度(octave),同時增益每減半一次振幅就衰減 6 個分貝(6dB),因此這一響應又被稱為 6dB/octave 濾波。
但盡管類似圖 2 的圖示在音樂界中被廣泛應用,它其實并不準確。圖 3 為一個更精確的傳遞函數圖示。

圖 3:較為精確的 RC 低通濾波器響應圖示
可以看到,信號在截止頻率的位置已經衰減了 3dB。這并不是一個錯誤,實際上,在電工學中截止頻率就是信號衰減 3dB 的位置。所以本文要總結的第一條規律就是:
被動低通濾波器在什么位置開始工作并不是由截止頻率決定的;截止頻率是信號已經衰減了 3dB 的位置。另外,由于 3dB 的衰減可以輕易被人耳感知,這也就意味著,信號在截止頻率的位置已經受到了明顯的影響。
讓我們回過頭來想想看簡易的低通濾波器會對常見波形產生什么樣的影響。簡單起見,我們將以圖 2 中的理想低通濾波器為例,因為它的尖銳「拐點」能夠將濾波器的工作簡化許多。

圖 4:鋸齒波的前 200 個諧波
圖 4 是最常見的模擬合成器波形之一——鋸齒波的諧波結構。其所有諧波均存在,各諧波的幅度與基頻幅度呈 1/n 的簡單關系(n 為諧波次數)。

圖 5:使用對數軸表示的上述 100Hz 鋸齒波的諧波結構
圖 4 展示的使用傳統單位表示的鋸齒波的前 200 個諧波的幅度。然而,與圖 4 相比,使用圖 5 中的對數軸來展示這些諧波要合適得多。但即使你不懂什么是對數也沒有關系,因為盡管圖 4 與圖 5 看起來很不同,兩者其實表示的是同樣的信息。之所以我在這里選擇使用對數圖表是因為使用對數表示的振幅是一條直線,因此能夠更明確地展示濾波器對其的影響。實際上,如果你回過頭來觀察圖 2 和圖 3,這兩張圖中使用的其實也是對數軸。

圖 6:3kHz,6dB/octave 低通濾波器對于 100Hz 鋸齒波的影響
假如說我們有一個截止頻率為 3kHz 的 6dB/octave RC 濾波器,讓我們來看看它會對基頻為 100Hz 的鋸齒波造成什么樣的影響。圖 6 展示的是該濾波器對于 3kHz 以上的頻率的衰減。不難發現圖 6 中的圖形與圖 5 相比有一個「折疊」,該圖形符合上文提到的 6dB/octave 的規律。

圖 7 - 8:理想狀態下的 100Hz 鋸齒波波形(上);經 3kHz 濾波器處理過的該鋸齒波波形(下)
現在再看圖 7 與圖 8,圖 7 展示的是上文中理想狀態下 100Hz 鋸齒波的波形,圖 8 則是經過我們的 3kHz 濾波器處理過的該鋸齒波。盡管這兩個波形在視覺方面并沒有太大的區別,因為 3kHz 的截止頻率允許該波形的前三十個諧波通過,只有低幅度的高頻諧波收到影響,但由于人耳十分敏銳,當你將這兩個波形對比來聽的時候,很明顯可以聽到經過濾波的波形更加「暗淡」,或者缺乏「高頻」。
6dB/octave 的濾波器被廣泛運用于音響系統的音色控制單元中,偶爾也被合成器用來作為輔助功能的亮度控制,但它們通常不會被真正的音色合成所使用。這是因為它們通常不會對音色造成明顯的變化——經過 6dB/octave 濾波器處理的波形聽起來就像是原來的波形一樣,只不過更暗淡了一些。顯然,要想創造全新的音色我們還需要更強大的濾波器。
所以我們需要使用什么樣的被動元件才可以制造出 12dB/octave、18 dB/octave、甚至 24dB/octave 的濾波器呢?不幸的是,沒有任何被動元件可以滿足這樣的需求,所以我們需要一個不同的手段。為什么不把一系列的的 RC 濾波器組合起來從而得到我們需要的更陡峭的頻率響應呢?比如說兩個 RC 濾波器組合起來可以得到一個 12dB/octave 濾波器,疊加三個就可以得到 18dB/octave 濾波器,四個則是 24dB/octave…理想狀態下這樣的由四個 RC 濾波器疊加組成的電路與圖 9 看起來類似。如果這一濾波器工作正常,其理想狀態下的傳遞函數則應該類似于圖 10 中所展示的圖形。

圖 9:由四個 6dB/octave 濾波器疊加組成的 24dB/octave 低通 RC 濾波器

圖 10:上述假想的 24dB/octave 對于高頻諧波的衰減
然而濾波器的工作方式并沒有想象中的這么簡單。我們的被動 RC 濾波器響應模型對于其輸入與輸出值需要有一定的假設,盡管單一的 RC 電路可以滿足這一要求,但如果你將多個這樣的電路疊加在一起,得到的響應則將會完全不同。所以我們到底應該怎樣才可以制造出我們需要的濾波器呢?
如果你已經對合成器有所了解了的話,你可能聽說過 12dB/octave 有時又被稱作「2-pole」濾波器,24dB/octave 濾波器被稱為「4-pole」濾波器。所以你可能因此而假設圖 9 中的每個 6dB/octave 的模塊為一個「pole」。然而這樣的假設并不準確。
其實「2-pole」、「4-pole」這樣的名字是由一個叫做「拉普拉斯變換」的數學運算的結果。這一變換可以方便數學家們分析音頻信號的線形響應(至于什么是「線性系統」以及其背后的數學原理由于其過于復雜,本文將不予探討)。總而言之,我們之所以用「pole」來描述濾波器,是因為 RC 濾波器的拉普拉斯變換圖表看起來像是一個由帳篷柱支撐起來的橡膠平面。單一的 6dB/octave 濾波器有一個這樣的「帳篷柱」,因此被稱為「1-pole」濾波器,12dB/octave 的濾波器則有兩個這樣的「帳篷柱」,以此類推…

圖 11:1-pole(左)、2-pole(中)與 3-pole(右)濾波器的拉普拉斯變換圖示
因此,如果你想制造一個 24dB/octave 單一截止頻率的被動 RC 濾波器的話,你需要使得四個 pole 處在圖中的同一位置。但正如我之前的說明,使用被動元件不可能達到這樣的效果,因為多個被動元件之間會產生交互,組合起來的被動元件的工作方式與單一被動元件的工作方式并不相同。所以說,四個 6dB/octave RC 濾波器組成的頻率響應并不能達到圖 10 中的理想效果,反之,實際情況中我們會得到的是一條具有四個「拐點」的傳遞函數曲線,如圖 12。

圖 12:由四個 6dB/octave 濾波器疊加構成的傳遞函數曲線
我們因此可以得到一個重要的結論:盡管被動 4-pole 濾波器在高頻位置會接近于于 24dB/octave 的響應,但在某些頻段中,其響應會多少與 6dB/octave、12dB/octave、以及 18dB/octave 類似。另外,如果你仔細觀察上面的圖線,你可以發現中間的這些區域并不是精確的直線,也就是說頻率與輸入輸出的信號并不像之前那樣直接。
盡管我們設計了一個理論上具備 24dB/octave 的電路,但由于濾波器之間的相互作用,其各自的截止頻率都不盡相同。另外,每個截止頻率出的拐點都是圓滑的,并且就算四個分濾波器的截止頻率完全一致,合成起來的拐點也不會因此變得「尖銳」。而且,我們還忽略了其對于截止頻率以下的頻率造成的影響,低于截止頻率的信號理論上不應該受到濾波器的影響,但實際上由于上述濾波器的工作原理,其截止頻率以下的信號也會遭到一定程度上的衰減,并且還有可能產生一些其他我們不想要的結果。還有最后一點:我們還完全忽略了每個分濾波器對于波形相位造成的偏移。
聽到這里你也許會想,擁有這么多副作用的濾波器八成沒有什么實用性,但實際上我們可以通過為上述濾波器的電路中的每個濾波器之間添加一些元件,使它們之間的響應彼此分離(或者「緩沖」),因此解決上述的部分問題。這些元件包括運算放大器(operational amplifiers),通常被簡稱為「op-amp,運放」。運放等元件使得濾波器由「被動」變為「主動」。
不難想象,幾乎所有模擬合成器中使用的濾波器均為主動濾波器(一小部分亮度控制或者基礎均衡器中可能會用到被動濾波)。主動濾波器要比被動濾波器更加復雜,但它們的優勢在于,在設計合理的情況下,你可以很容易地使他們以你需要的方式運作。比如說,有些濾波器會專注于在截止頻率處保證一個尖銳的拐點;有些濾波器保證截止頻率以下的信號盡量不受改變;還有一些濾波器能夠實現某些獨特的相位響應…不過這些優點很難同時實現,所以與錄音設備制造的許多其他方面類似,好的濾波器設計通常是在各種優點之間權衡取舍的結果。
但還有另外一個因素需要考慮:即便是我們在討論這些濾波器的基本問題的時候,我們也都認為電路中的各個元件是「理想」的。然而實際上許多電子元件的實際參數與其標稱參數相差百分之一或者百分之二,甚至有時候相差百分之十幾都是正常的情況。這也就意味著即便是兩個表面上完全一致的電路之間通常也會有些許細微的差異。還以之前的 24dB/octave 濾波器為例,四個「pole」之間完全對齊的可能性非常之小。這也意味著我們之前對于被動濾波器總結的結論其實可以廣泛適用:
4-pole 濾波器總會在高頻位置接近于 24dB/octave,但在某些頻段中也會表現出 6dB/octave、12dB/octave、以及 18dB/octave 的響應。
說了這么多,我們不難發現:濾波器的工作原理要比我們預想中復雜得多得多。盡管 Minimoog 和 ARP 合成器中都使用了 24dB/octave 濾波器,但兩者的聽感卻明顯不同。同樣,MS20 與 Oberheim SEM 中的 12dB/octave 濾波器給人的聽感彼此也大相徑庭。所以,作為本文的最后一條結論,我想說的是:
不管彼此的差別是否明顯,每種模擬濾波器的設計所造成的聽感都會有所不同。
在設計濾波器的時候,運用一些技巧可以克服濾波器本身的固有缺陷。比如說,Marc Paping 在設計他的 Fénix 半模塊化合成器的時候使用了一個 5-pole 設計(其理論上具備 30dB/octave 的響應),從而使得 Fénix 的「Moog 風格」低通濾波器實現了真正的 24dB/octave。
另一方面,設計濾波器的時候也很容易犯錯。一個簡單的計算錯誤導致了運用于某些 ARP 合成器中的臭名昭著的 ARP4075 濾波器。理論上這應該是一個頂尖水準的濾波器,但設計缺陷導致了其截止頻率無法達到 12kHz 以上,因此使得運用了該濾波器的合成器聽起來十分「渾濁」、「死氣沉沉」。神奇的是,只需要換掉電路板上的四個電阻就可以簡單地修復這一問題。
-
電感器
+關注
關注
20文章
2335瀏覽量
70705 -
均衡器
+關注
關注
9文章
219瀏覽量
30392 -
音頻濾波器
+關注
關注
0文章
6瀏覽量
6453 -
拉普拉斯變換
+關注
關注
1文章
32瀏覽量
10177 -
信號衰減器
+關注
關注
0文章
5瀏覽量
1223
發布評論請先 登錄
相關推薦
單片機的深入了解!
示波器的深入了解
一文了解有源濾波器與無源濾波器的區別
深入了解表面貼裝型晶體濾波器:DSF753S 2POLE、DSF753S 3POLE 和 DSF753S 4POLE
一文了解5G射頻前端模組中的濾波器




 深入了解濾波器的原理
深入了解濾波器的原理














評論