Smith圓圖是什么？

是由菲利普·史密斯(Phillip Smith)于1939年發明的，由很多圓周交織在一起的一個圖，是反射系數的極坐標圖。史密斯曾經說過：“在我能夠使用計算尺的時候，我對以圖標方式來表達數學上的關聯很有興趣。”

Smith圓圖常用于協助解決傳輸線問題和阻抗匹配問題。本文將為大家介紹使用方法。

相關參數

01

反射系數

信號沿傳輸線向前傳播時，每時每刻都會感受到一個瞬態阻抗，這個阻抗可能是傳輸線本身的，也可能是中途或末端其他元件的。對于信號來說，它不會區分到底是什么，信號所感受到的只有阻抗。如果信號感受到的阻抗是恒定的，那么他就會正常向前傳播，只要感受到的阻抗發生變化，不論是什么引起的（可能是中途遇到的電阻，電容，電感，過孔，PCB轉角，接插件），信號都會發生反射。

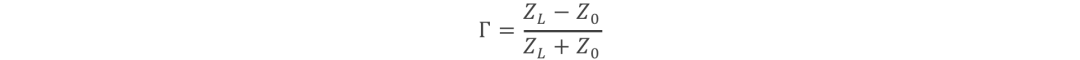
歸一化負載阻抗：

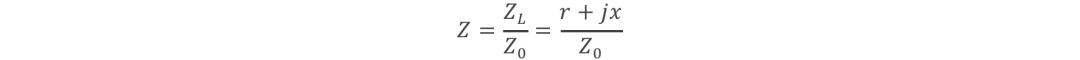
得到：

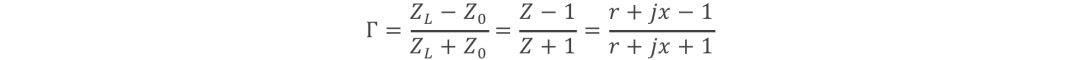
當中的Γ代表其線路的反射系數(reflection coefficient)Z是歸一負載值，即ZL/ Z0。當中，ZL是線路本身的負載值，Z0是傳輸線的特征阻抗（本征阻抗）值，通常會使用50Ω。

02

駐波比

駐波比全稱為電壓駐波比，又名VSWR和SWR，為英文Voltage Standing Wave Ratio的簡寫。指駐波波腹電壓與波谷電壓幅度之比，又稱為駐波系數、駐波比。駐波比等于1時，表示饋線和天線的阻抗完全匹配，此時高頻能量全部被天線輻射出去，沒有能量的反射損耗；駐波比為無窮大時，表示全反射，能量完全沒有輻射出去。

駐波比可以通過反射系數來計算得出：

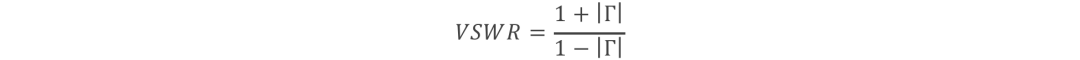
03

S11

S11實際上就是反射系數Г，只不過它特指一個網絡1號端口的反射系數。反射系數描述的是入射電壓和反射電壓之間的比值，而回波損耗是從功率的角度來看待問題。RL=-S11。

04

阻抗

在具有電阻、電感和電容的電路里，對電路中的電流所起的阻礙作用叫做阻抗。阻抗常用Z表示，是一個復數，實部稱為電阻，虛部稱為電抗，其中電容在電路中對交流電所起的阻礙作用稱為容抗,電感在電路中對交流電所起的阻礙作用稱為感抗，電容和電感在電路中對交流電引起的阻礙作用總稱為電抗。阻抗的單位是歐姆。

電阻：

電容：

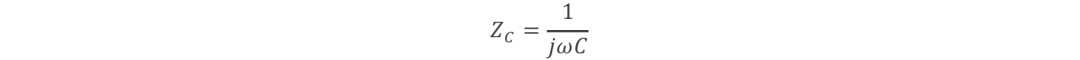
電感：

阻抗：

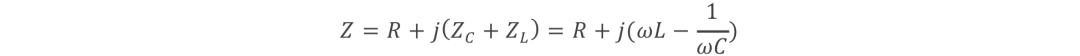
因為電容和電感的存在，它會是一個復數。

（1）如果(ωL–1/ωC) > 0，稱為“感性負載”；

（2）反之，如果(ωL–1/ωC)<0，稱為“容性負載”；

如果電路中只有電阻，它只會影響信號的幅度，如下圖所示：

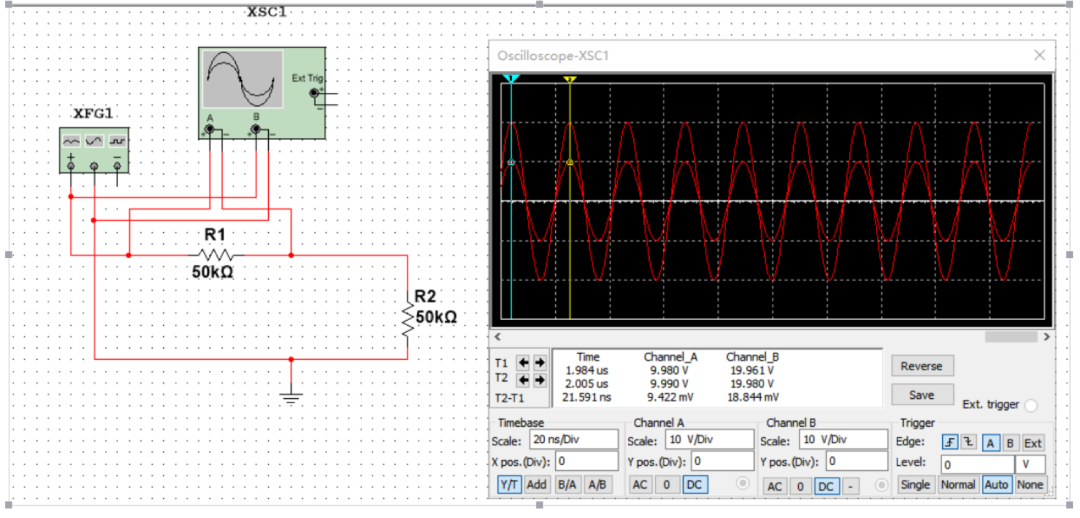
如果電路中不僅存在電阻，還存在電感及電容時，不僅會影響信號幅度，同時相位、頻率特性也會發生變化，所以計算過程中即需要考慮實部，也需要考慮虛部。如下圖所示：

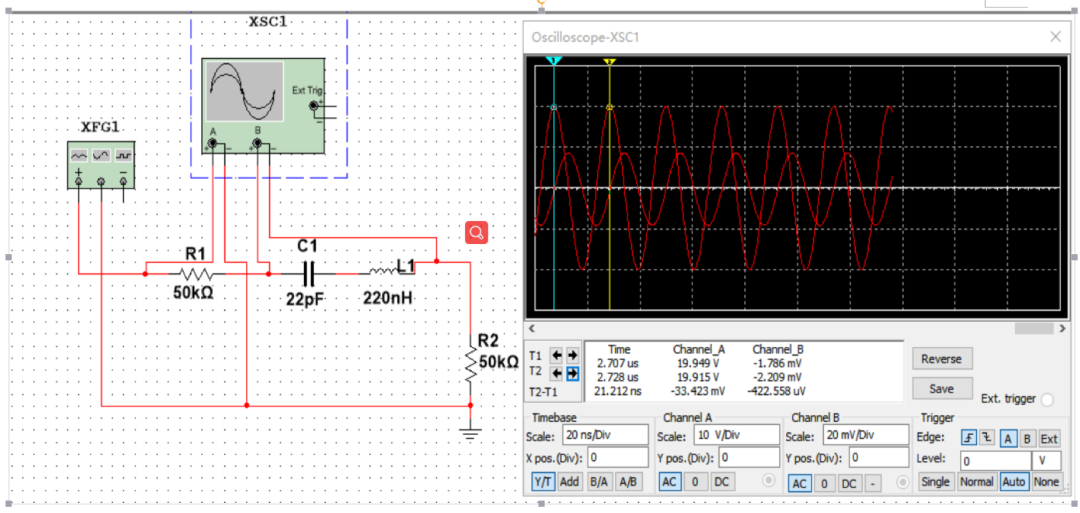
如何記住Smith圓

我們可以在一個復平面里面，以實部為x軸、以虛部為y軸，表示任意一個復數。我們的阻抗，不管多少電阻、電容、電感串聯、并聯，之后，都可以表示在一個復平面里面。

在RLC 串聯電路中，交流電源電壓U = 220 V，頻率f = 50 Hz，R = 30Ω，L =445 mH，C =32 mF。

綜上可得：

X（L）=2πfL≈140Ω

X（C）=1/2πfC≈100Ω

則：

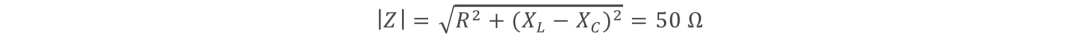
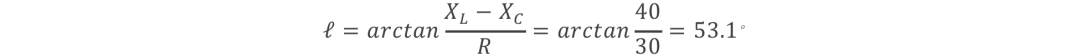
在復平面中表示：

各種阻抗的情況，組成了這個無窮大的平面。

下面就開始方便我們去記住Smith圓圖，我們將進行"變身“：

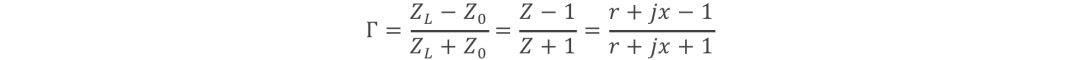
將復平面圖，進行扭曲變成圓，變身過程如下：

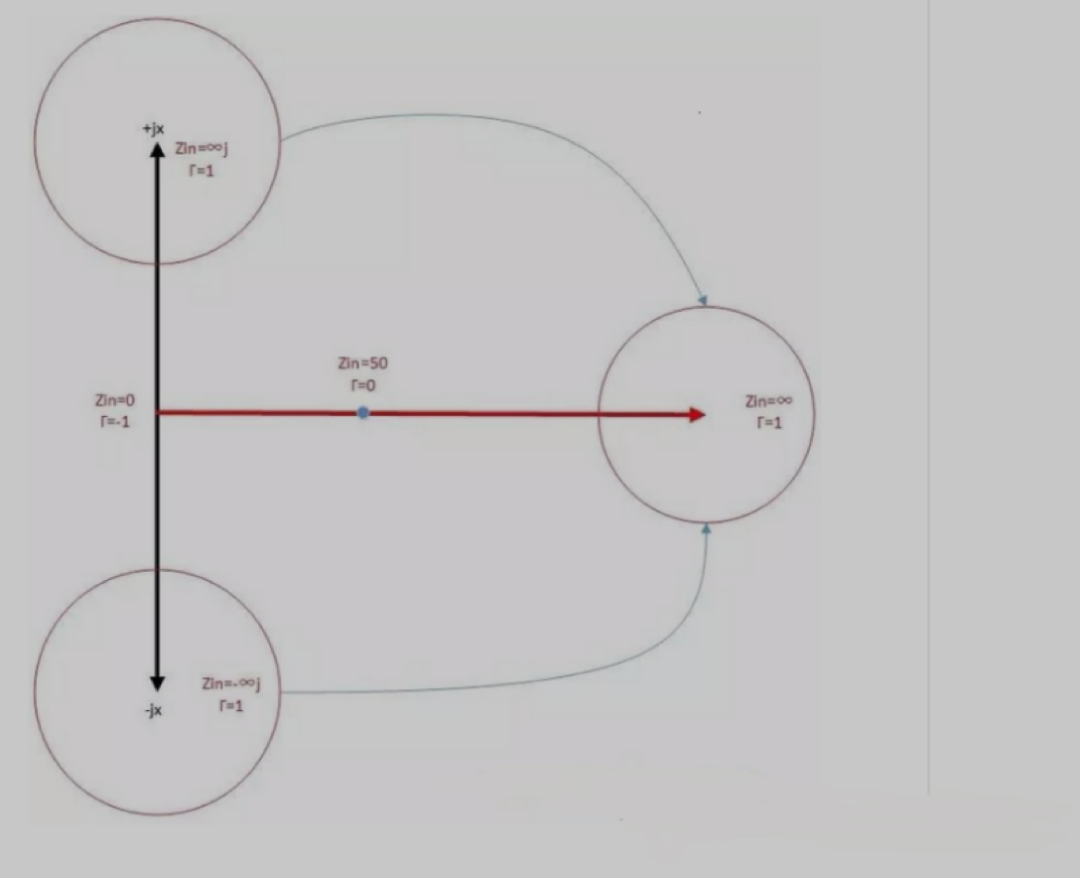
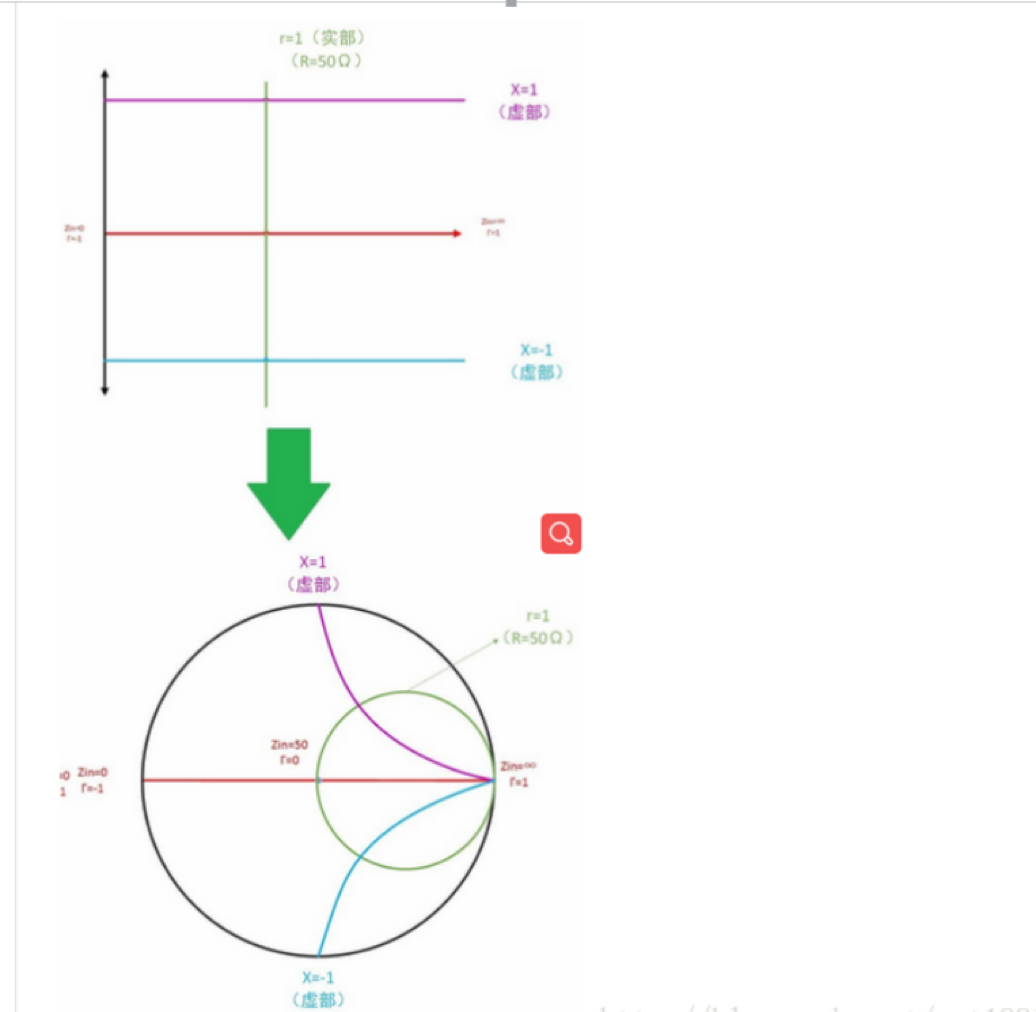
紅色的線上的阻抗，有個特點：虛部為0；（電感、電容為0）

紫色的線上的阻抗，有個特點：虛部為-1；

藍色的線上的阻抗，有個特點：虛部為1；

Smith圓圖操作

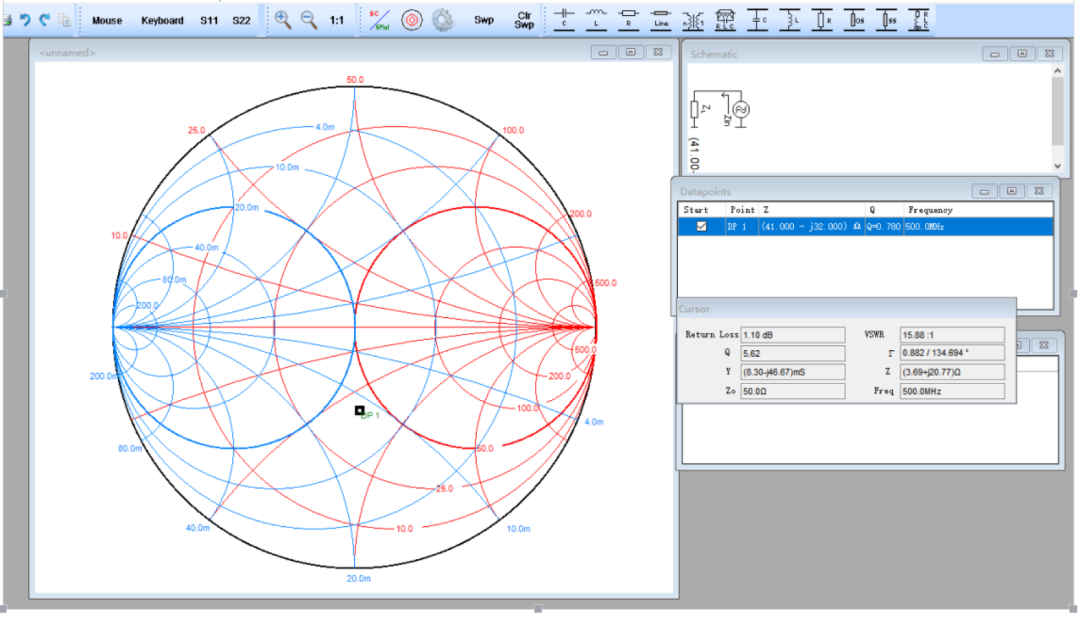
紅色是阻抗圖，綠色是導納圖；

上半圓表示感性負載，下半圓表示容性負載，中間紅線表示純電阻；

串聯器件看阻抗圖：

（1）串聯電感順時針移（增加感性）

（2）串聯電容逆時針移（增加容性）

并聯器件看導納圖:

（1）并聯電感逆時針移（增加感性）

（2）并聯電容順時針移（增加容性）

總之，都是往增加該器件屬性的方向移動；

比如上圖P1點需要往中心點靠，可以先阻抗圖順時針轉，再導納圖順時針轉，即通過串電感，再并電容。如下圖，串聯16.2nH電感到P2點，再并聯3.0pF電容到P3點。

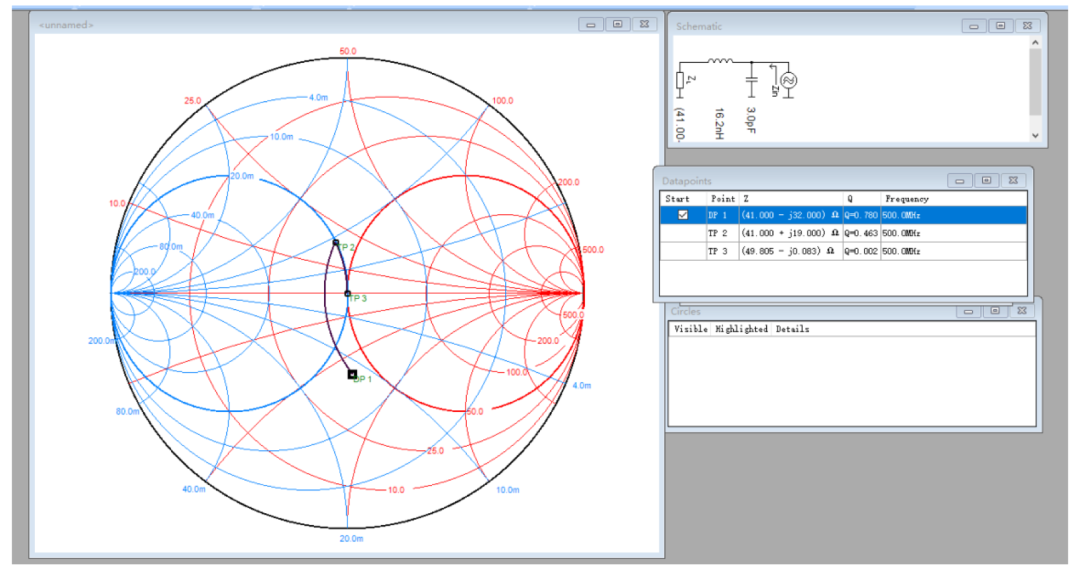
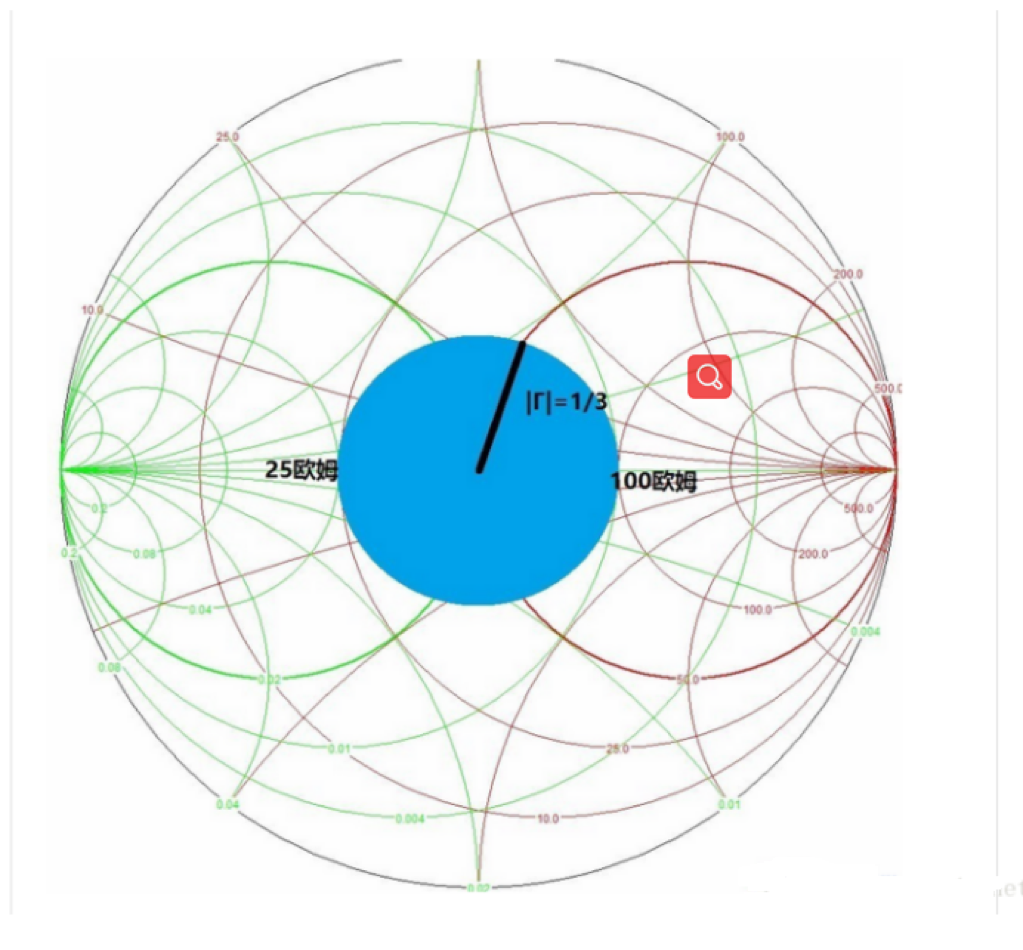
平時做阻抗匹配時不可能完全做到匹配后反射系數為0，通常希望反射系數絕對值小于1/3(這時對應RL≈-10dB，VSWR≈2，反射率≈11%)，即下圖藍色區域。

正確的使用Smith圓圖，可以在不作任何計算的前提下得到一個表面上看非常復雜的系統的匹配阻抗，唯一需要作的就是沿著圓周線讀取并跟蹤數據。