三電容電路

作為基本π網絡的一種，三電容電路是理解模擬電路頻響、放大器穩(wěn)定性、開關-電容放大器、開關-電容積分器、采樣保持放大器的基礎。從多種不同的角度深刻理解三電容電路是模擬電路設計入門的關鍵，同時 三電容電路也是各大電路公司面試常用的題型 。

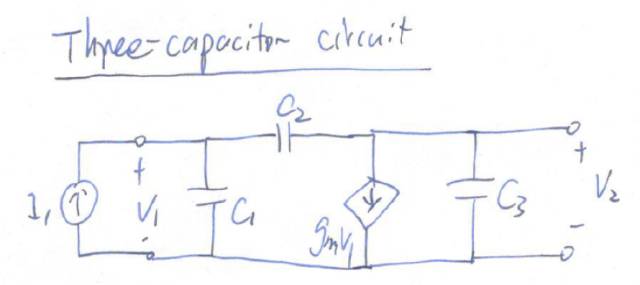
首先，這個電路有三個電容，但是三個電容形成一個環(huán)，電路只有兩個獨立的狀態(tài)變量（state variable），所以這個電路的傳輸函數只有兩個極點。

零極點的位置如下圖，有一個極點在原點，注意有一個零點在右半平面。

假設拉普拉斯域I 1 (s) 為 1，或者時域i 1 (t)為1*δ(t)，我們可以通過拉普拉斯反變換找出v 2 (t)：

我們發(fā)現(xiàn)，v 2 (t) 由一個階躍項和一個指數項組成，指數項會衰減到0，但是階躍項會一直保持。合在一起的總響應就是一開始有一個反向的過沖（overshoot），然后會以指數衰減的方式穩(wěn)定到一個固定的終值。

現(xiàn)在我們換一種方式來分析零極點。之前我們講過，極點是由電路的純粹的拓撲結構所定的，每一個網絡函數都有一樣的極點。

三電容電路零極點分析

現(xiàn)在我們來看這個純粹的電路。假設這個電路是零狀態(tài)的（relaxed），那么這個電路是線性時不變的（LTI），所以C1 C2組成了一個分壓器，那么我們可以用V1來表示V 2 。

但是V2由是受控源兩端的電壓，而這個受控源也受到V1的控制，所以就變成了壓控電流源被自己兩端電壓所控制。 一個被自己電壓控制的電流源就是一個電阻 。所以我們可以算出該電阻：

于是，三電容電路變成了下圖。這個電路的時間常量很好算了，算出來果然跟我們之前算的一個極點吻合。

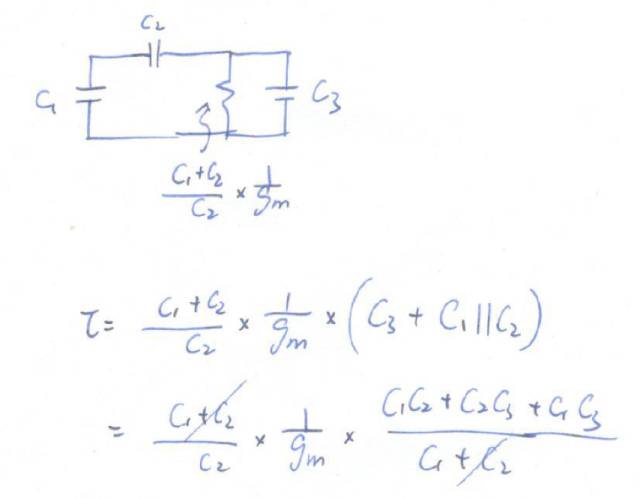
另一個極點呢？

我們現(xiàn)在假設C2 C3上的t=0- 時的初始狀態(tài)為這樣：

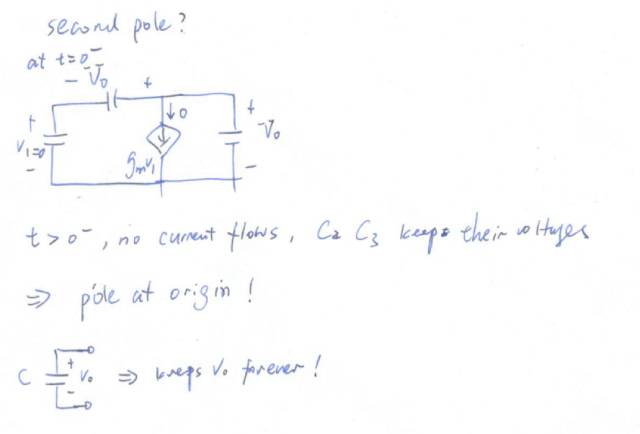
當t=0時，我們發(fā)現(xiàn)整個電路沒有電流，C2 C3上的電壓一直保持著，這種能夠保持初始狀態(tài)的網絡，一定有一個極點在原點。我們可以舉一個最簡單的例子，一個電容可以保持電壓，所以電容的阻抗這個網絡函數有一個極點在原點。

這也與我們之前的推導吻合。

現(xiàn)在找零點，我們之前學過，零點是很特別的，是由激勵和響應的相對位置決定的。找零點需要抵消響應。現(xiàn)在我們把響應V2 抵消掉，如圖：

那么C3沒有電流，受控源的電流等于C2的電流，但是C2的電流由可以被直接用V1表示出來，所以：

三電容電路時域分析

然后， 我們從時域的角度把三電容電路的機理再過一次 （非常重要！是深入理解三電容電路并幫你通過面試拿到offer的關鍵！）。

我們必須要先理解沖激電流的物理意義。單位沖激電流在拉普拉斯域的表示為1。注意這個1是有單位的，單位是庫倫，大家可以思考一下為什么電流的拉普拉斯轉換的單位是庫倫。在時域里，單位沖激函數前面的1的單位也是庫倫，因為單位沖激函數的積分為1，但是電流的積分必須是庫倫，所以這里的1代表了一個包裹的1庫倫電荷，這個1庫倫的電荷只需要0時間就可以被輸送，因為在t=0的時候，電流無窮大。

所以，單位沖激電流的物理意義就是用0時間通過無窮大的電流向一個高斯面里輸送了1庫倫電荷。

現(xiàn)在回到三電容電路，在t=0-時，三個電容都沒有初始電荷。在t=0時，1庫倫的電荷被注入到了紅色高斯面里。現(xiàn)在的問題是，會不會有有限量的電荷在t=0時流入綠色高斯面。我們來分析這個情況：

如果有有限量的電荷流入綠色高斯面，那說明受控源gmv1必須是無窮大，因為無窮大的電流才能在0時間內輸送有限的電荷，有限的電流在0時間內輸送0電荷。

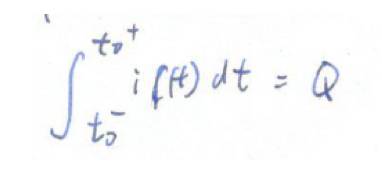
這表示v1是無窮大，但是v1無窮大的話，紅色高斯面內必須有無窮大的電荷，這不可能，因為沖激電流所攜帶的電荷是有限的。所以受控源電流是有限的，受控源在0時間內不輸送任何電荷。所以在t=0+時，只有電荷會在C1 C2 C3 中重新分布，1庫倫的電荷會在C 1 +C 2 ||C3這個總電容上建立一個電壓v 1 (0+)。C2 和C3必須形成一個分壓器，因為C2的右極板和C3的上極板的電荷總和為0。這樣我們可以推出v 2 (0+)：

化簡v 2 (o+)，我們可以得到：

這跟我們之前用拉普拉斯轉換得到的結果一致 ！

下面看最終狀態(tài)，當電路達到最終狀態(tài)時，所有的狀態(tài)變量都不再改變了（除非我們有共振或者不穩(wěn)定的特殊情況，然而這個電路顯然沒有），這說明受控源gmv1必須為0，v1必須為0。但是當t>0時，紅色高斯面內的電荷就不再會改變了，因為獨立電流源為0，所以所有1庫倫的電荷都必須被“擠壓”到C2上，產生電壓1/C 2 。因為v 1 (∞)為0，所以我們可以算出v 2 (∞)為-1/C2。

這又跟我們用拉普拉斯轉換得到的結果一致 ！

我們之已經分析過，這個電路只有一個非無窮大的時間常量，所以這是一個“準一階電路”。對于這種電路，只要我們知道在t=0+的初始值和t=∞的終值，中間的行為就是一個一階指數衰減。所以我們得到與之前一致的響應：

引入非理想效應

接著我們引入一個不理想效應，在受控源處并聯(lián)一個電導G 3 （有沒有覺得下面的電路圖很熟悉？對了，就是MOSFET小信號電路基本就長這樣）。

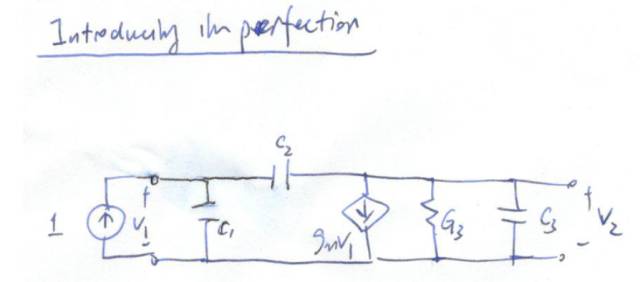
重新使用基本π型函數列出傳輸函數：

使用拉普拉斯反變換，我們得到

這里，D0成為了誤差項，如果要讓D0非常接近于1，gmR3要遠大于1+C 1 /C 2 。

我們來從時域角度看這個問題：

如果G3不為0，那么在終值狀態(tài)時，會有一個循環(huán)的電流流過G 3 。所以gmv1不為0，那么v1不為0。這樣，并非所有的1庫倫電荷都被“擠壓”到了C2上，這就是導致誤差項的原因。對于模擬電路而言，我們希望精確地放大信號，放大倍數最好是元件之間的比例。假如我們的沖激電流源變成了vsC1δ(t)，或者說C1 采樣了一個電壓源v s ，C1在t=0時被放置到三電容電路里，如果G3為0，那么響應v2終值將為準確的電容比例-C 2 /C1 v s 。但如果G3不為0，這個比例就會有誤差。

三電容電路實際應用

看到這里，大家一定會認為我們會拿MOSFET小信號電路作為例子吧？非也，我們當然要找一個更有趣的例子。下面由焦魔為大家講一個三電容電路的實例：開關電容積分器（SCIntegrator）。

開關電容積分器是有源梯形濾波器（Active Ladder Filter）的基本組成模塊。相比于使用電阻電容有源濾波器（OpAmp RC Filter），開關電容濾波器（SC Filter）具有精度高，噪聲小，受工藝、電壓、溫度影響小的優(yōu)點（原因是我們不再需要電阻這個在芯片上很難做準的元件了）。下圖所示為一種基本的開關電容積分器（前向歐拉型，F(xiàn)orward Euler）的電路。

注：在該電路圖中，梯形符號代表跨導放大器（Operational Transconductance Amplifier, OTA）。跨導放大器和我們熟悉的運算放大器非常容易混淆，前者使用梯形符號，后者則是三角形符號。運算放大器的模型是一個壓控電壓源，跨導放大器的模型是一個壓控電流源。嚴格來講，我們通常所說的集成電路中的運算放大器實際上都是指跨導放大器；而我們做板級電路設計時使用的運放芯片才是真正的運算放大器。

該電路有兩個工作相位。在φ1相位，電容C1的電壓跟隨輸入電壓vi變化，φ1相位結束時電容C1的電壓即為φ2相位開始時的初始電壓。φ2相位時電路的小信號模型如下圖右側所示。其中沖激電流源等效代表了C1的初始電壓。電路的時序和波形圖如下：

電容C1在每個周期的采樣值在tk時刻確定，輸出電壓在每個周期φ2的開始時刻開始變化，先有一個瞬時的前向饋通，然后以指數衰減的形式穩(wěn)定到最終的電壓值，理想情況下電壓的變化量由電容C1和C2的比值以及tk時刻采樣的輸入電壓值決定。同時，上一個周期存在C2上的電荷并沒有被釋放，所以這個電路就變成了一個積分器。如果考慮OTA有限的輸出電阻，這個電壓變化量會有一定的偏差。