在做信號處理的過程中，常遇到將信號補零后再做FFT等操作，比如頻域脈沖壓縮算法中，一般距離維PRT數據和脈壓系數需要填零使長度相等且滿足2的N次方，但是填零操作能做什么，不能做什么呢？

先說結論：補零不會改變頻譜的樣子（輪廓），也就是不會改變頻率分辨率，但會減弱柵欄效應，提高頻譜分辨率，也就是頻譜采樣點會增加，導致頻譜采樣間隔減小。注意，頻譜分辨率和頻率分辨率的區別。

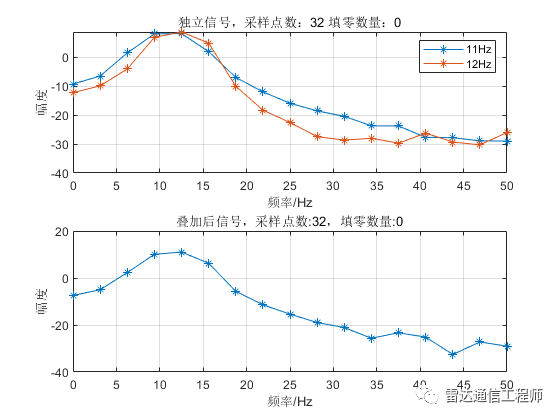
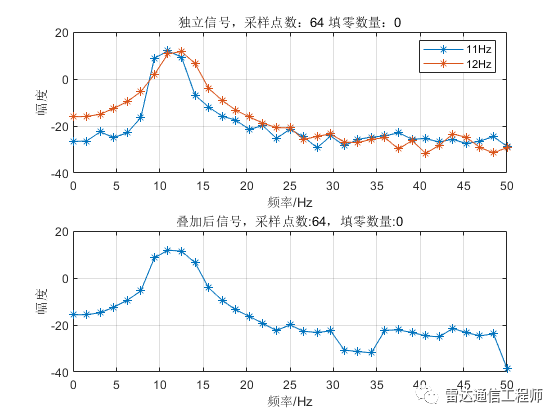
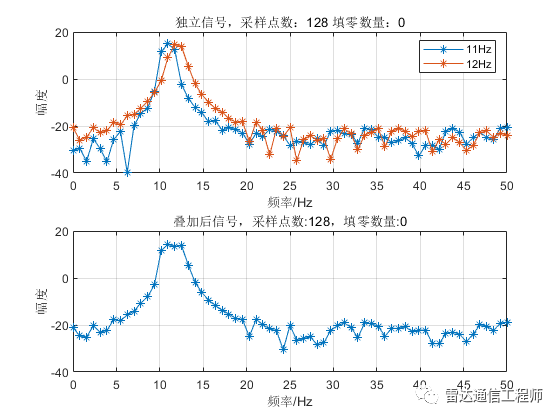
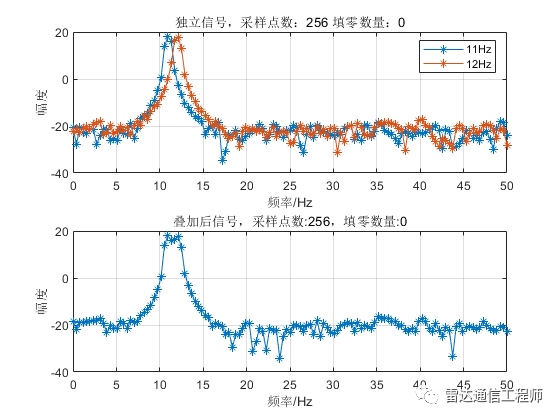
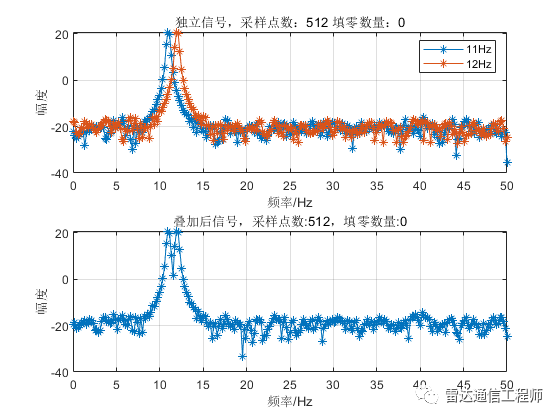
示例中使用100Hz采樣率產生兩個單頻點正弦信號，頻率分別為11、12Hz；接著兩者分別做FFT運算，以及兩信號疊加后做FFT；

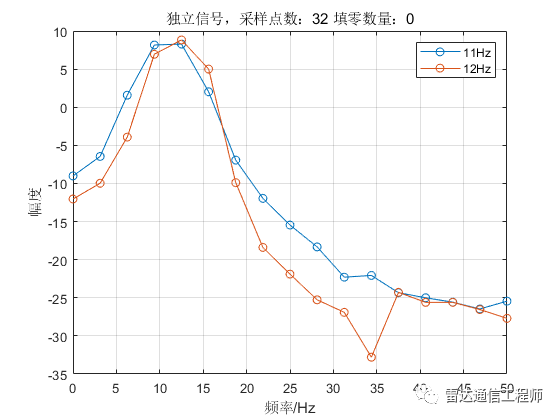
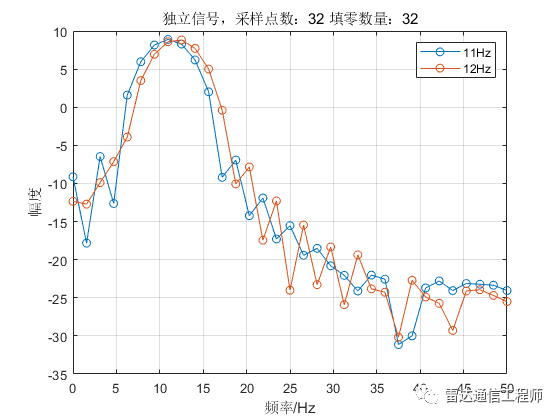
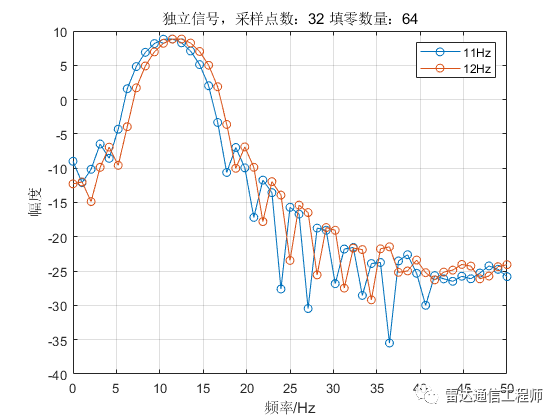
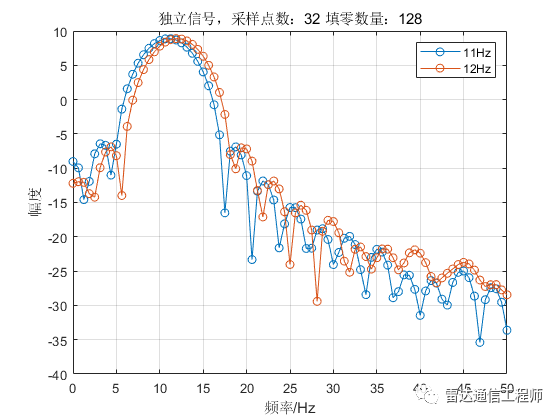
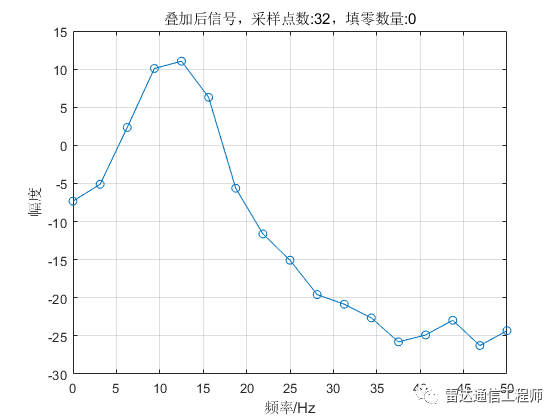
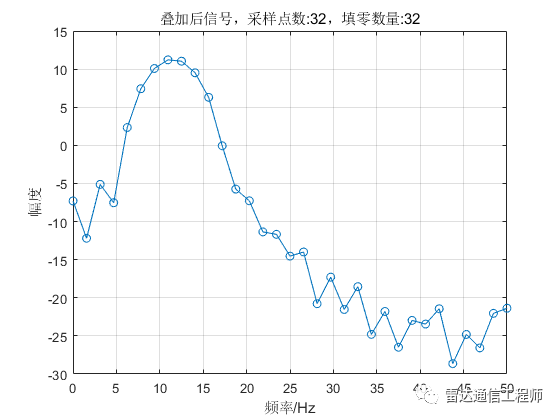
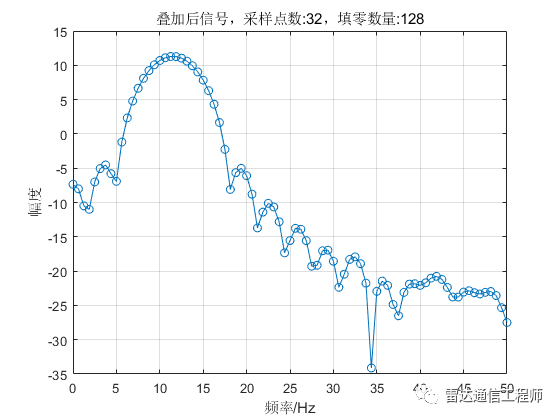
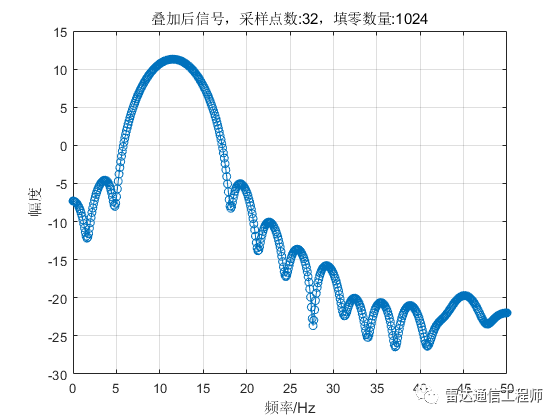
從以上各圖可以看出，隨著填零數量的增加，頻譜的基本輪廓并未改變，只是變得更細膩（提高了頻率顆粒度，即頻譜分辨率），但是并不能提高頻率分辨率，從圖形上直觀體現為主瓣尖峰寬度不變，圖中11Hz和12Hz的正弦信號頻譜峰值難以分辨；

從原理上分析，采樣率100Hz，N=32點，則FFT頻率分辨率fs/N=3.125Hz，則本例中1Hz的差異是無法分辨的，不斷的填充0相當于在頻域進行插值，隨著填零數量的增加，32點的FFT信號頻譜將不斷逼近離散時間傅里葉變換（DTFT）的結果；反過來理解（將圖按從下往上的順序看），在N=32不變的情況下，填零后FFT相當于在32點信號DTFT結果中一個頻域周期內進行等間隔采樣而來。

提高頻率分辨率需要增加觀測時間（即有效數據長度），如需要分辨1Hz的頻率，就需要至少1/1Hz=1s的有效觀測時長；下面看看增加采樣點數后頻譜的變化，圖中分別有11、12Hz兩個頻率的獨立頻譜和時域疊加后的頻譜，可以看到在N大于128點開始，疊加信號主瓣上開始出現兩個非相鄰獨立峰值點，N越大，區分越明顯。單頻信號的主瓣寬度隨著N增加而變窄。