1 數(shù)據(jù)準(zhǔn)備
首先引入相關(guān)的 statsmodels,包含統(tǒng)計(jì)模型函數(shù)(時(shí)間序列)。
# 引入相關(guān)的統(tǒng)計(jì)包
import warnings # 忽略警告
warnings.filterwarnings('ignore')
import numpy as np # 矢量和矩陣
import pandas as pd # 表格和數(shù)據(jù)操作
import matplotlib.pyplot as plt
import seaborn as sns
from dateutil.relativedelta import relativedelta # 有風(fēng)格地處理日期
from scipy.optimize import minimize # 函數(shù)優(yōu)化
import statsmodels.formula.api as smf # 統(tǒng)計(jì)與經(jīng)濟(jì)計(jì)量
import statsmodels.tsa.api as smt
import scipy.stats as scs
from itertools import product
from tqdm import tqdm_notebook
import statsmodels.api as sm
用真實(shí)的手機(jī)游戲數(shù)據(jù)作為樣例,研究每小時(shí)觀看的廣告數(shù)和每日所花的游戲幣。
# 1 如真實(shí)的手機(jī)游戲數(shù)據(jù),將調(diào)查每小時(shí)觀看的廣告和每天花費(fèi)的游戲幣
ads = pd.read_csv(r'./test/ads.csv', index_col=['Time'], parse_dates=['Time'])
currency = pd.read_csv(r'./test/currency.csv', index_col=['Time'], parse_dates=['Time'])
2 穩(wěn)定性
建模前,先來了解一下穩(wěn)定性(stationarity)。
如果一個(gè)過程是平穩(wěn)的,這意味著它不會(huì)隨時(shí)間改變其統(tǒng)計(jì)特性,如均值和方差等等。
方差的恒常性稱為同方差,協(xié)方差函數(shù)不依賴于時(shí)間,它只取決于觀測(cè)值之間的距離。
非平穩(wěn)過程是指分布參數(shù)或者分布規(guī)律隨時(shí)間發(fā)生變化。也就是說,非平穩(wěn)過程的統(tǒng)計(jì)特征是時(shí)間的函數(shù)(隨時(shí)間變化)。
下面的紅色圖表不是平穩(wěn)的:
- 平均值隨時(shí)間增加
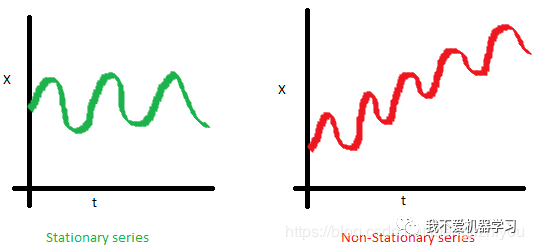
- 方差隨時(shí)間變化

- 隨著時(shí)間的增加,距離變得越來越近。因此,協(xié)方差不是隨時(shí)間而恒定的

為什么平穩(wěn)性如此重要呢? 通過假設(shè)未來的統(tǒng)計(jì)性質(zhì)與目前觀測(cè)到的統(tǒng)計(jì)性質(zhì)不會(huì)有什么不同,可以很容易對(duì)平穩(wěn)序列進(jìn)行預(yù)測(cè)。
大多數(shù)的時(shí)間序列模型,以這樣或那樣的方式,試圖預(yù)測(cè)那些屬性(例如均值或方差)。
如果原始序列不是平穩(wěn)的,那么未來的預(yù)測(cè)將是錯(cuò)誤的。
大多數(shù)時(shí)間序列都是非平穩(wěn)的,但可以(也應(yīng)該)改變這一點(diǎn)。
平穩(wěn)時(shí)間序列的類型:
- 平穩(wěn)過程(stationary process):產(chǎn)生平穩(wěn)觀測(cè)序列的過程。
- 平穩(wěn)模型(stationary model):描述平穩(wěn)觀測(cè)序列的模型。
- 趨勢(shì)平穩(wěn)(trend stationary):不顯示趨勢(shì)的時(shí)間序列。
- 季節(jié)性平穩(wěn)(seasonal stationary):不表現(xiàn)出季節(jié)性的時(shí)間序列。
- 嚴(yán)格平穩(wěn)(strictly stationary):平穩(wěn)過程的數(shù)學(xué)定義,特別指觀測(cè)值的聯(lián)合分布不受時(shí)移的影響。
若時(shí)序中有明顯的趨勢(shì)和季節(jié)性,則對(duì)這些成分建模,將它們從觀察中剔除,然后用殘差訓(xùn)練建模。
平穩(wěn)性檢查方法(可以檢查觀測(cè)值和殘差):
- 看圖:繪制時(shí)序圖,看是否有明顯的趨勢(shì)或季節(jié)性,如繪制頻率圖,看是否呈現(xiàn)高斯分布(鐘形曲線)。
- 概括統(tǒng)計(jì):看不同季節(jié)的數(shù)據(jù)或隨機(jī)分割或檢查重要的差分,如將數(shù)據(jù)分成兩部分,計(jì)算各部分的均值和方差,然后比較是否一樣或同一范圍內(nèi)
- 統(tǒng)計(jì)測(cè)試:選用統(tǒng)計(jì)測(cè)試檢查是否有趨勢(shì)和季節(jié)性
若時(shí)序的均值和方差相差過大,則有可能是非平穩(wěn)序列,此時(shí)可以對(duì)觀測(cè)值取對(duì)數(shù),將指數(shù)變化轉(zhuǎn)變?yōu)榫€性變化。然后再次查看取對(duì)數(shù)后的觀測(cè)值的均值和方差以及頻率圖。
上面前兩種方法常常會(huì)欺騙使用者,因此更好的方法是用統(tǒng)計(jì)測(cè)試 sm.tsa.stattools.adfuller()。
接下來將學(xué)習(xí)如何檢測(cè)穩(wěn)定性,從白噪聲開始。
# 5經(jīng)濟(jì)計(jì)量方法(Econometric approach)
# ARIMA 屬于經(jīng)濟(jì)計(jì)量方法
# 創(chuàng)建平穩(wěn)序列
white_noise = np.random.normal(size=1000)
with plt.style.context('bmh'):
plt.figure(figsize=(15,5))
plt.plot(white_noise)

標(biāo)準(zhǔn)正態(tài)分布產(chǎn)生的過程是平穩(wěn)的,在0附近振蕩,偏差為1。現(xiàn)在,基于這個(gè)過程將生成一個(gè)新的過程,其中每個(gè)后續(xù)值都依賴于前一個(gè)值。
def plotProcess(n_samples=1000,rho=0):
x=w=np.random.normal(size=n_samples)
for t in range(n_samples):
x[t] = rho*x[t-1]+w[t]
with plt.style.context('bmh'):
plt.figure(figsize=(10,5))
plt.plot(x)
plt.title('Rho {}\\n Dickey-Fuller p-value: {}'.format(rho,round(sm.tsa.stattools.adfuller(x)[1],3)))
#-------------------------------------------------------------------------------------
for rho in [0,0.6,0.9,1]:
plotProcess(rho=rho)




第一張圖與靜止白噪聲一樣。
第二張圖,ρ增加至0.6,大的周期出現(xiàn),但整體是靜止的。
第三張圖,偏離0均值,但仍然在均值附近震蕩。
第四張圖,ρ= 1,有一個(gè)隨機(jī)游走過程即非平穩(wěn)時(shí)間序列。當(dāng)達(dá)到臨界值時(shí), 不返回其均值。從兩邊減去 ,得到 ,左邊的表達(dá)式被稱為 一階差分 。
如果 ρ= 1,那么一階差分等于平穩(wěn)白噪聲 。這是 Dickey-Fuller時(shí)間序列平穩(wěn)性測(cè)試 (測(cè)試單位根的存在)背后的主要思想。
如果 可以用一階差分從非平穩(wěn)序列中得到平穩(wěn)序列,稱這些序列為1階積分 。 該檢驗(yàn)的零假設(shè)是時(shí)間序列是非平穩(wěn)的 ,在前三個(gè)圖中被拒絕,在最后一個(gè)圖中被接受。
1階差分并不總是得到一個(gè)平穩(wěn)的序列,因?yàn)檫@個(gè)過程可能是 d 階的積分,d > 1階的積分(有多個(gè)單位根)。在這種情況下,使用增廣的Dickey-Fuller檢驗(yàn),它一次檢查多個(gè)滯后時(shí)間。
可以使用不同的方法來去除非平穩(wěn)性:各種順序差分、趨勢(shì)和季節(jié)性去除、平滑以及轉(zhuǎn)換如Box-Cox或?qū)?shù)轉(zhuǎn)換。
3 SARIMA
接下來開始建立ARIMA模型,在建模之前需要將非平穩(wěn)時(shí)序轉(zhuǎn)換為平穩(wěn)時(shí)序。
3.1 去除非穩(wěn)定性
擺脫非平穩(wěn)性,建立SARIMA(Getting rid of non-stationarity and building SARIMA)
def tsplot(y,lags=None,figsize=(12,7),style='bmh'):
"""
Plot time series, its ACF and PACF, calculate Dickey-Fuller test
y:timeseries
lags:how many lags to include in ACF,PACF calculation
"""
ifnot isinstance(y, pd.Series):
y = pd.Series(y)
with plt.style.context(style):
fig = plt.figure(figsize=figsize)
layout=(2,2)
ts_ax = plt.subplot2grid(layout, (0,0), colspan=2)
acf_ax = plt.subplot2grid(layout, (1,0))
pacf_ax = plt.subplot2grid(layout, (1,1))
y.plot(ax=ts_ax)
p_value = sm.tsa.stattools.adfuller(y)[1]
ts_ax.set_title('Time Series Analysis Plots\\n Dickey-Fuller: p={0:.5f}'.format(p_value))
smt.graphics.plot_acf(y,lags=lags, ax=acf_ax)
smt.graphics.plot_pacf(y,lags=lags, ax=pacf_ax)
plt.tight_layout()
#-------------------------------------------------------------------------------------
tsplot(ads.Ads, lags=60)

從圖中可以看出,Dickey-Fuller檢驗(yàn)拒絕了單位根存在的原假設(shè)(p=0);序列是平穩(wěn)的,沒有明顯的趨勢(shì),所以均值是常數(shù),方差很穩(wěn)定。
唯一剩下的是季節(jié)性,必須在建模之前處理它。可以通過季節(jié)差分去除季節(jié)性,即序列本身減去一個(gè)滯后等于季節(jié)周期的序列。
ads_diff = ads.Ads-ads.Ads.shift(24) # 去除季節(jié)性
tsplot(ads_diff[24:], lags=60)
ads_diff = ads_diff - ads_diff.shift(1) # 去除趨勢(shì)
tsplot(ads_diff[24+1:], lags=60) # 最終圖


第一張圖中,隨著季節(jié)性的消失,自回歸好多了,但是仍存在太多顯著的滯后,需要?jiǎng)h除。首先使用一階差分,用滯后1從自身中減去時(shí)序。
第二張圖中,通過季節(jié)差分和一階差分得到的序列在0周圍震蕩。Dickey-Fuller試驗(yàn)表明,ACF是平穩(wěn)的,顯著峰值的數(shù)量已經(jīng)下降,可以開始建模了。
3.2 建 SARIMA 模型
SARIMA:Seasonal Autoregression Integrated Moving Average model。
是簡(jiǎn)單自回歸移動(dòng)平均的推廣,并增加了積分的概念。
- AR (p): 利用一個(gè)觀測(cè)值和一些滯后觀測(cè)值之間的依賴關(guān)系的模型。模型中的最大滯后稱為p。要確定初始p,需要查看PACF圖并找到最大的顯著滯后,在此之后大多數(shù)其他滯后都變得不顯著。
- I (d): 利用原始觀測(cè)值的差值(如觀測(cè)值減去上一個(gè)時(shí)間步長(zhǎng)的觀測(cè)值)使時(shí)間序列保持平穩(wěn)。這只是使該系列固定所需的非季節(jié)性差分的數(shù)量。在例子中它是1,因?yàn)槭褂昧艘浑A差分。
- MA (q):利用觀測(cè)值與滯后觀測(cè)值的移動(dòng)平均模型殘差之間的相關(guān)性的模型。目前的誤差取決于前一個(gè)或前幾個(gè),這被稱為q。初始值可以在ACF圖上找到,其邏輯與前面相同
每個(gè)成分都對(duì)應(yīng)著相應(yīng)的參數(shù)。
SARIMA(p,d,q)(P,D,Q,s) 模型需要選擇趨勢(shì)和季節(jié)的超參數(shù)。
趨勢(shì)參數(shù) ,趨勢(shì)有三個(gè)參數(shù),與ARIMA模型的參數(shù)一樣:
- p: 模型中包含的滯后觀測(cè)數(shù),也稱滯后階數(shù)。
- d: 原始觀測(cè)值被差值的次數(shù),也稱為差值度。
- q:移動(dòng)窗口的大小,也叫移動(dòng)平均的階數(shù)
季節(jié)參數(shù) :
- S(s):負(fù)責(zé)季節(jié)性,等于單個(gè)季節(jié)周期的時(shí)間步長(zhǎng)
- P:模型季節(jié)分量的自回歸階數(shù),可由PACF推導(dǎo)得到。但是需要看一下顯著滯后的次數(shù),是季節(jié)周期長(zhǎng)度的倍數(shù)。如果周期等于24,看到24和48的滯后在PACF中是顯著的,這意味著初始P應(yīng)該是2。P=1將利用模型中第一次季節(jié)偏移觀測(cè),如t-(s*1)或t-24;P=2,將使用最后兩個(gè)季節(jié)偏移觀測(cè)值t-(s * 1), t-(s * 2)
- Q:使用ACF圖實(shí)現(xiàn)類似的邏輯
- D:季節(jié)性積分的階數(shù)(次數(shù))。這可能等于1或0,取決于是否應(yīng)用了季節(jié)差分。
可以通過分析ACF和PACF圖來選擇趨勢(shì)參數(shù),查看最近時(shí)間步長(zhǎng)的相關(guān)性(如1,2,3)。
同樣,可以分析ACF和PACF圖,查看季節(jié)滯后時(shí)間步長(zhǎng)的相關(guān)性來指定季節(jié)模型參數(shù)的值。
現(xiàn)在知道了如何設(shè)置初始參數(shù),查看最終圖并設(shè)置參數(shù)。
上面倒數(shù)第一張圖就是最終圖:
- p:最可能是4,因?yàn)樗荘ACF上最后一個(gè)顯著的滯后,在這之后,大多數(shù)其他的都不顯著。
- d:為1,因?yàn)槲覀冇?jì)算了一階差分
- q:應(yīng)該在4左右,就像ACF上看到的那樣
- P:可能是2,因?yàn)?4和48的滯后對(duì)PACF有一定的影響
- D:為1,因?yàn)橛?jì)算了季節(jié)差分
- Q:可能1,ACF的第24個(gè)滯后顯著,第48個(gè)滯后不顯著。
下面看不同參數(shù)的模型表現(xiàn)如何:
# 建模 SARIMA
# setting initial values and some bounds for them
ps = range(2,5)
d=1
qs=range(2,5)
Ps=range(0,2)
D=1
Qs=range(0,2)
s=24#season length
# creating list with all the possible combinations of parameters
parameters=product(ps,qs,Ps,Qs)
parameters_list = list(parameters)
print(parameters)
print(parameters_list)
print(len(parameters_list))
# 36
def optimizeSARIMA(parameters_list, d,D,s):
"""
Return dataframe with parameters and corresponding AIC
parameters_list:list with (p,q,P,Q) tuples
d:integration order in ARIMA model
D:seasonal integration order
s:length of season
"""
results = []
best_aic = float('inf')
for param in tqdm_notebook(parameters_list):
# we need try-exccept because on some combinations model fails to converge
try:
model = sm.tsa.statespace.SARIMAX(ads.Ads, order=(param[0], d,param[1]),
seasonal_order=(param[2], D,param[3], s)).fit(disp=-1)
except:
continue
aic = model.aic
# saving best model, AIC and parameters
if aic< best_aic:
best_model = model
best_aic = aic
best_param = param
results.append([param, model.aic])
result_table = pd.DataFrame(results)
result_table.columns = ['parameters', 'aic']
# sorting in ascending order, the lower AIC is - the better
result_table = result_table.sort_values(by='aic',ascending=True).reset_index(drop=True)
return result_table
%%time
result_table = optimizeSARIMA(parameters_list, d,D,s)
result_table.head()
# set the parameters that give the lowerst AIC
p,q,P,Q = result_table.parameters[0]
best_model = sm.tsa.statespace.SARIMAX(ads.Ads, order=(p,d,q),seasonal_order=(P,D,Q,s)).fit(disp=-1)
print(best_model.summary()) # 打印擬合模型的摘要。這總結(jié)了所使用的系數(shù)值以及對(duì)樣本內(nèi)觀測(cè)值的擬合技巧。
# inspect the residuals of the model
tsplot(best_model.resid[24+1:], lags=60)
parameters aic
0 (2, 3, 1, 1) 3888.642174
1 (3, 2, 1, 1) 3888.763568
2 (4, 2, 1, 1) 3890.279740
3 (3, 3, 1, 1) 3890.513196
4 (2, 4, 1, 1) 3892.302849
Statespace Model Results
==========================================================================================
Dep. Variable: Ads No. Observations: 216
Model: SARIMAX(2, 1, 3)x(1, 1, 1, 24) Log Likelihood -1936.321
Date: Sun, 08 Mar 2020 AIC 3888.642
Time: 23:06:23 BIC 3914.660
Sample: 09-13-2017 HQIC 3899.181
- 09-21-2017
Covariance Type: opg
==============================================================================
coef std err z P >|z| [0.0250.975]
------------------------------------------------------------------------------
ar.L1 0.79130.2702.9280.0030.2621.321
ar.L2 -0.55030.306-1.7990.072-1.1500.049
ma.L1 -0.73160.262-2.7930.005-1.245-0.218




 時(shí)序分析實(shí)戰(zhàn)之SARIMA、Linear model介紹
時(shí)序分析實(shí)戰(zhàn)之SARIMA、Linear model介紹