數(shù)學(xué)將成為第一門借助AI實(shí)現(xiàn)重大突破的學(xué)科?
去年 2 月份,DeepMind 發(fā)布了編程輔助利器 AlphaCode。它使用人工智能技術(shù)來(lái)幫助程序員更快地編寫(xiě)代碼,可以自動(dòng)完成代碼、提供代碼建議并檢查錯(cuò)誤,從而提高編程效率。AlphaCode 的問(wèn)世意味著 AI 在解決現(xiàn)實(shí)世界問(wèn)題的道路上又邁出了一大步。
巧合的是,在同一天,OpenAI 也展示了一項(xiàng)重要成果:他們開(kāi)發(fā)的神經(jīng)定理證明器成功解出了兩道國(guó)際奧數(shù)題。這一成果是在微軟打磨了多年的數(shù)學(xué) AI——Lean 的基礎(chǔ)上完成的。Lean 于 2013 年推出,數(shù)學(xué)家可以把數(shù)學(xué)公式轉(zhuǎn)換成代碼,再輸入到 Lean 中,讓程序來(lái)驗(yàn)證定理是否正確。OpenAI 的成功表明,AI 不僅可以用于解決編程等應(yīng)用學(xué)科的問(wèn)題,還能用來(lái)攻克數(shù)學(xué)等自然學(xué)科。
值得注意的是,這并不是 AI 研究者的「一廂情愿」。就像快速接受 AlphaCode 的軟件工程師一樣,數(shù)學(xué)家也在越來(lái)越頻繁地使用 AI,比如獲得過(guò)菲爾茨獎(jiǎng)的陶哲軒。他甚至預(yù)言,到 2026 年,AI 將成為數(shù)學(xué)研究領(lǐng)域可信賴的合著者(co-author)。
與此同時(shí),主攻數(shù)學(xué)問(wèn)題的 AI 也在不斷發(fā)展壯大:一個(gè)名為 LeanDojo 的開(kāi)放平臺(tái)提供了一套基于大型語(yǔ)言模型的開(kāi)源定理證明器,消除了在機(jī)器學(xué)習(xí)方法用于定理證明時(shí)存在的私有代碼、數(shù)據(jù)和大量計(jì)算需求等障礙,為機(jī)器學(xué)習(xí)方法在定理證明領(lǐng)域的研究提供了便利。
「我相信,數(shù)學(xué)將成為第一門通過(guò)人工智能實(shí)現(xiàn)重大突破的學(xué)科。」在看到這些進(jìn)展之后,英偉達(dá)高級(jí) AI 研究科學(xué)家 Jim Fan 在一篇推特中預(yù)言說(shuō)。
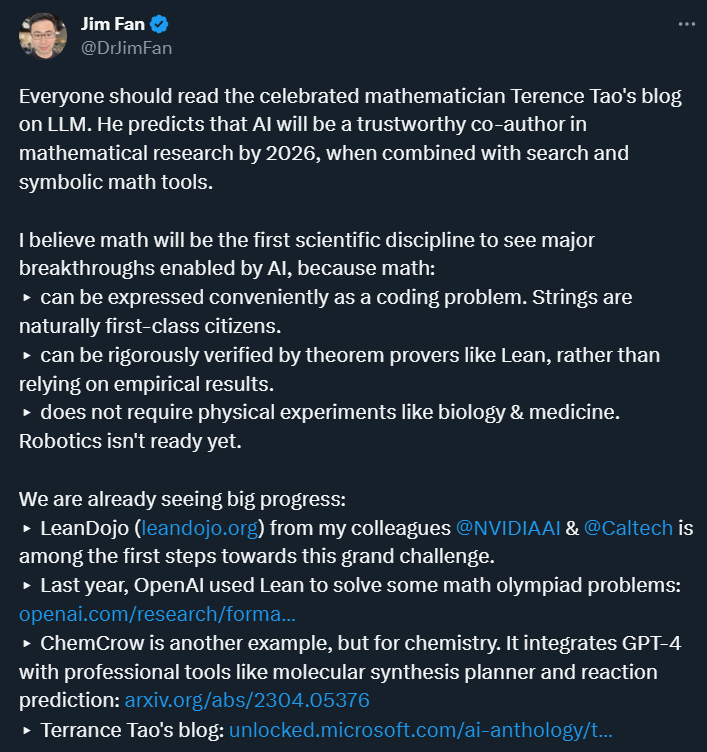
除了以上種種進(jìn)展,Jim Fan 還列出了以下推斷依據(jù):
-
數(shù)學(xué)可以被方便地轉(zhuǎn)化為編碼問(wèn)題,字符串在其中具有重要地位,這使得數(shù)學(xué)問(wèn)題可以通過(guò)人工智能工具進(jìn)行處理和分析;
-
與依賴實(shí)證結(jié)果的學(xué)科不同,數(shù)學(xué)可以通過(guò)定理證明器(如 Lean)進(jìn)行嚴(yán)格驗(yàn)證;
-
與需要依賴物理實(shí)驗(yàn)的學(xué)科(如生物學(xué)和醫(yī)學(xué))不同,數(shù)學(xué)不需要進(jìn)行物理實(shí)驗(yàn),無(wú)需依賴尚未完全成熟的機(jī)器人技術(shù)或?qū)嶒?yàn)設(shè)備。
在數(shù)學(xué)與 AI 的這場(chǎng)交叉之旅中,數(shù)學(xué)家和 AI 研究科學(xué)家在共同探索更多可能性。或許,陶哲軒和 Jim Fan 的預(yù)言都將加速實(shí)現(xiàn)。
在陶哲軒手里,AI 成了數(shù)學(xué)家的得力助手
「我預(yù)計(jì),如果使用得當(dāng),到 2026 年,AI 將成為數(shù)學(xué)研究和許多其他領(lǐng)域值得信賴的合著者。」數(shù)學(xué)家陶哲軒在前不久的一篇博客中說(shuō)道。
在眾多知名數(shù)學(xué)家中,陶哲軒是較早接受并發(fā)現(xiàn) ChatGPT 這類 AI 大模型數(shù)學(xué)價(jià)值的一個(gè)。早在今年 3 月份 ChatGPT 連雞兔同籠問(wèn)題都搞不定的時(shí)候,陶哲軒就給予了它肯定的態(tài)度,認(rèn)為這類大模型完全可以勝任一些輔助性質(zhì)的工作,比如幫數(shù)學(xué)研究者進(jìn)行語(yǔ)義搜索、生成一些提示。
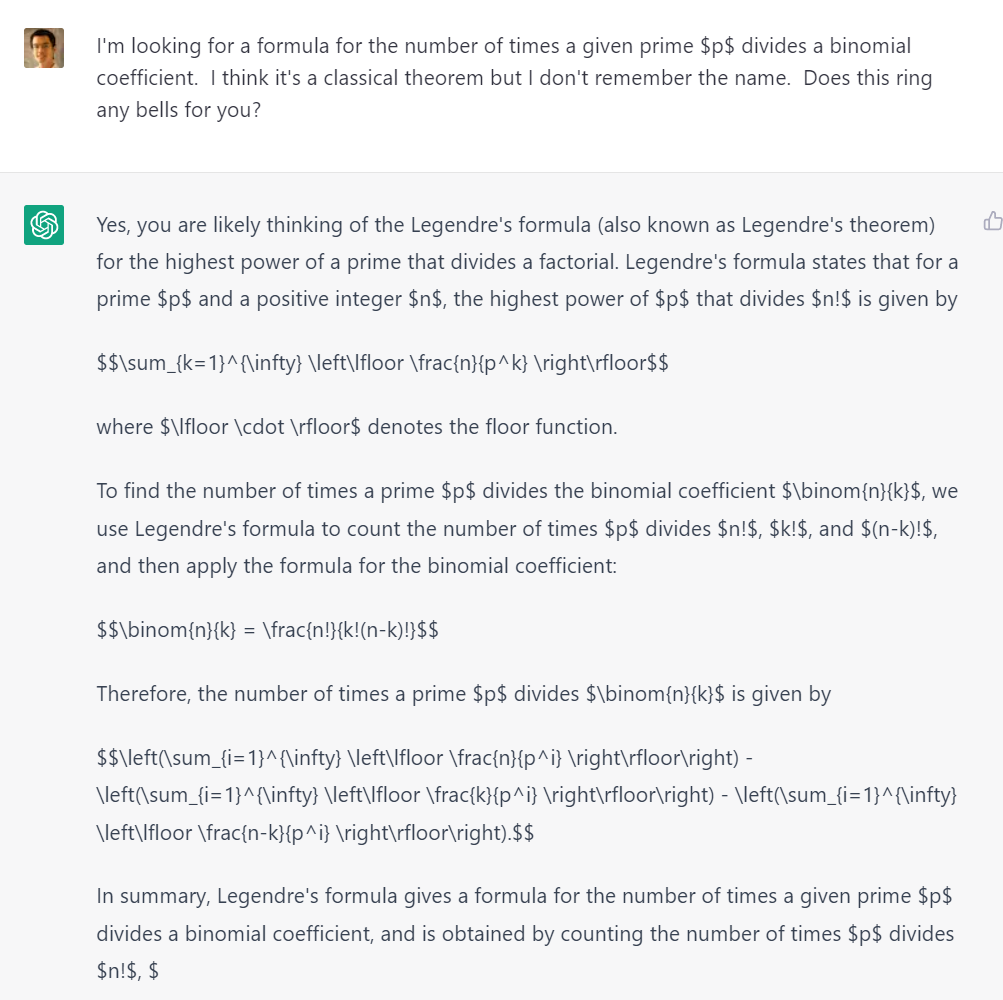
在這個(gè)例子中,陶哲軒提出的問(wèn)題是:「我在尋找一個(gè)關(guān)于 xx 的公式。我想這是一個(gè)經(jīng)典的定理,但我不記得名字了。你有什么印象嗎?」在這輪問(wèn)答中,雖然 ChatGPT 沒(méi)能給出正確答案(庫(kù)默爾定理),但根據(jù)它給出的近似答案(Legendre 公式),我們可以結(jié)合傳統(tǒng)搜索引擎輕松找到正確答案。
沒(méi)過(guò)多久,OpenAI 就發(fā)布了數(shù)學(xué)能力顯著提升的 GPT-4。陶哲軒也一直在嘗試解鎖這一強(qiáng)大的 AI 工具。
在使用過(guò)程中,他總結(jié)出了一些經(jīng)驗(yàn):不要試圖讓 AI 直接回答數(shù)學(xué)問(wèn)題(這樣得到的答案八成是廢話),而是讓它扮演合作者的角色,要求它提供策略建議。
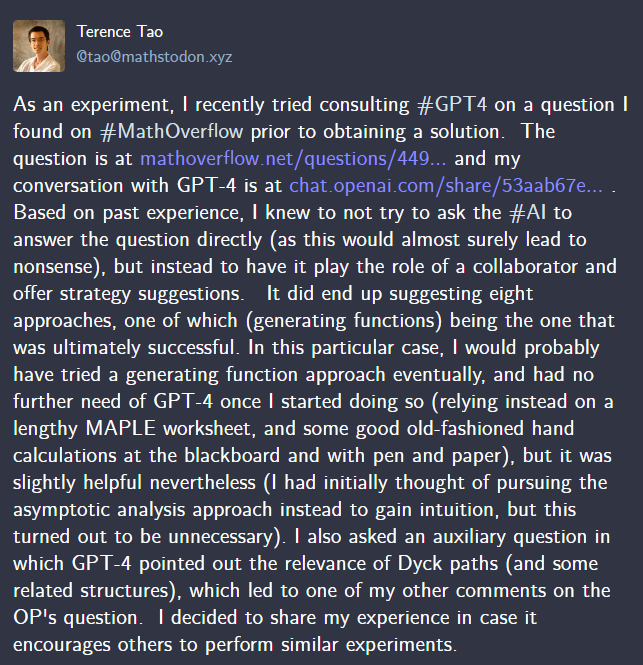
按照這種提示方法,陶哲軒在 GPT-4 的幫助下成功解決了一個(gè)數(shù)學(xué)證明題(GPT4 提出了 8 種方法,其中 1 種成功解決了問(wèn)題)。

陶哲軒利用 GPT-4 解決的問(wèn)題。

陶哲軒為了解決上述證明題提供給 GPT-4 的 Prompt:「你好,我是一名數(shù)學(xué)教授,我希望你能扮演一位善于提出解題技巧的數(shù)學(xué)專家合作者。我正試圖回答 MathOverflow 中的以下問(wèn)題……」
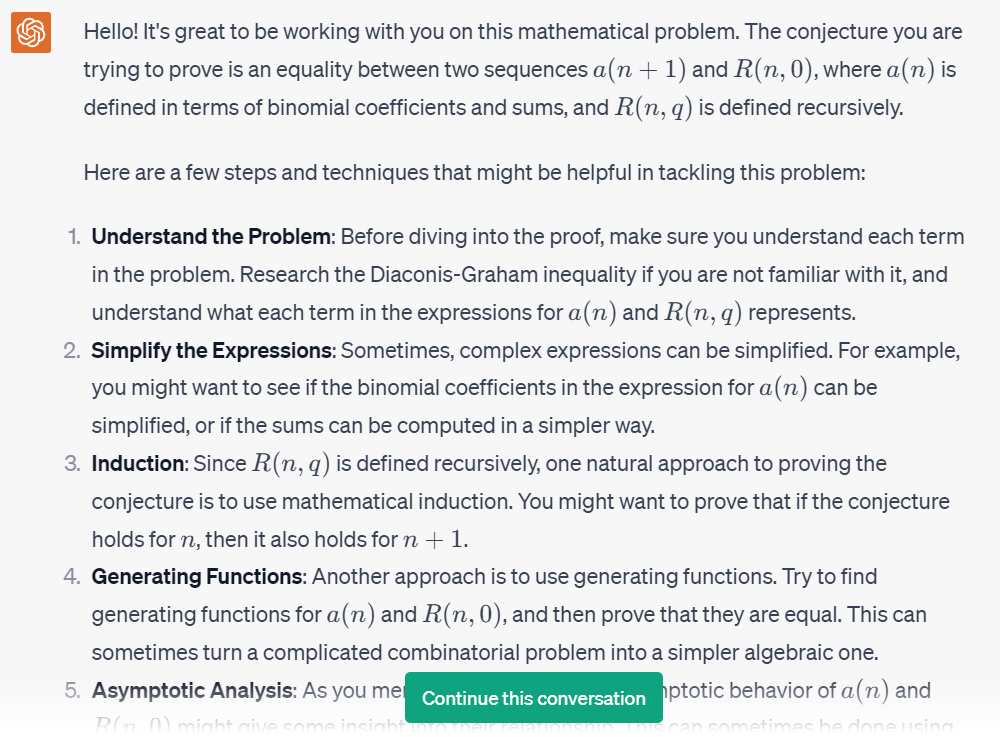
GPT-4 給出的部分建議。
當(dāng)然,除了這個(gè)證明題外,陶哲軒也在用 GPT-4 完成其他一些工作,包括但不限于:
-
提出問(wèn)題:他將最近一些數(shù)學(xué)預(yù)印本論文的前幾頁(yè)輸入給 GPT-4,并讓其生成一些與該論文相關(guān)的問(wèn)題,就像同行提出的問(wèn)題一樣。這可以幫助他更好地進(jìn)行演講準(zhǔn)備。
-
回答問(wèn)題:他現(xiàn)在經(jīng)常使用 GPT-4 來(lái)回答隨意和模糊的問(wèn)題,以前他可能會(huì)通過(guò)精心準(zhǔn)備的搜索引擎查詢來(lái)嘗試回答這些問(wèn)題;
-
輔助寫(xiě)作:他曾經(jīng)讓 GPT-4 給復(fù)雜文檔提供初稿建議,以輔助寫(xiě)作。
不過(guò),陶哲軒也指出,AI 在數(shù)學(xué)等學(xué)術(shù)領(lǐng)域的廣泛應(yīng)用對(duì)出版界和教育界來(lái)說(shuō)都是一個(gè)考驗(yàn):當(dāng)人工智能指導(dǎo)的研究生入門級(jí)數(shù)學(xué)論文可以在不到一天的時(shí)間內(nèi)生成時(shí),研究期刊將如何改變其出版和引用機(jī)制?我們的研究生教育方式將如何改變?我們會(huì)積極鼓勵(lì)和訓(xùn)練學(xué)生使用這些工具嗎?對(duì)于這些問(wèn)題,陶哲軒并沒(méi)有給出答案。
拿下數(shù)學(xué)定理證明,這項(xiàng)研究或讓陶哲軒預(yù)言早日成真
一直以來(lái),形式化的定理證明都是機(jī)器學(xué)習(xí)的重要挑戰(zhàn)。形式化證明本質(zhì)上是一種計(jì)算機(jī)程序,但與 C++ 或 Python 中的傳統(tǒng)程序不同,證明的正確性可以用證明助手(如開(kāi)頭提到的 Lean)來(lái)驗(yàn)證。定理證明是代碼生成的一種特殊形式,在評(píng)估上非常嚴(yán)格,沒(méi)有讓模型產(chǎn)生幻覺(jué)的空間。
這對(duì)目前的大型語(yǔ)言模型(LLM)來(lái)說(shuō)是有挑戰(zhàn)性的,盡管 LLM 在代碼生成方面表現(xiàn)出了優(yōu)秀的能力,但在事實(shí)性和幻覺(jué)性方面還有缺陷。
以往,對(duì)于用于定理證明的 LLM 研究面臨著許多障礙:比如,現(xiàn)有的基于 LLM 的證明器沒(méi)有一個(gè)是開(kāi)源的;它們都使用私有的預(yù)訓(xùn)練數(shù)據(jù),而且計(jì)算要求可以達(dá)到數(shù)千個(gè) GPU 時(shí);此外,有些基礎(chǔ)設(shè)施是依賴于為分布式訓(xùn)練和與證明助手的互動(dòng)而定制的,如果沒(méi)有開(kāi)源代碼,這兩者是不可能完全復(fù)現(xiàn)的。
在最近的一項(xiàng)研究中,來(lái)自加州理工學(xué)院、英偉達(dá)等機(jī)構(gòu)的研究者在該命題的解決進(jìn)程上走出了重要一步,提出了開(kāi)放平臺(tái) LeanDojo。

論文鏈接:https://arxiv.org/pdf/2306.15626.pdf
項(xiàng)目主頁(yè):https://leandojo.org/
總體來(lái)說(shuō),該研究有如下貢獻(xiàn):
-
首先,介紹了從 Lean 中提取數(shù)據(jù)并與之交互的工具;
-
第二,開(kāi)發(fā)了第一個(gè)用于定理證明的檢索增強(qiáng)的語(yǔ)言模型 ReProver;
-
第三,為基于學(xué)習(xí)的定理證明構(gòu)建了一個(gè)具有挑戰(zhàn)性的基準(zhǔn),并利用它來(lái)驗(yàn)證 ReProver 的有效性;
-
最后,公開(kāi)發(fā)布數(shù)據(jù)、模型和代碼,推動(dòng)了對(duì)定理證明的 LLM 的研究。
LeanDojo 的誕生有望改變當(dāng)前現(xiàn)狀:從開(kāi)源工具包、模型到基準(zhǔn),LeanDojo 讓研究人員能夠以適度的計(jì)算成本獲得最先進(jìn)的基于 LLM 的證明器。ReProver 不依賴私人數(shù)據(jù)集,并且可以在一周內(nèi)在單個(gè) GPU 上完成訓(xùn)練。
研究細(xì)節(jié)
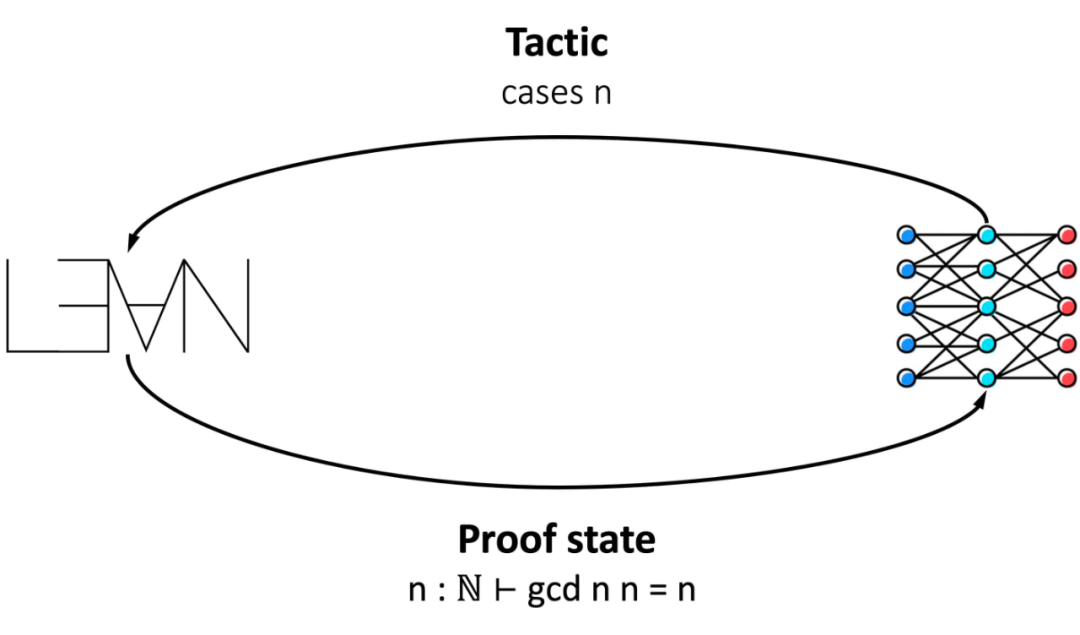
Lean 是一種編程語(yǔ)言,既可以寫(xiě)傳統(tǒng)的程序,也可以寫(xiě)定理和證明。它提供了兩個(gè)機(jī)制:首先,基于具有依賴類型的函數(shù)式編程,Lean 為定義程序、數(shù)學(xué)對(duì)象、定理和證明提供了一種統(tǒng)一的語(yǔ)言;第二,Lean 提供了一個(gè)策略系統(tǒng)(tactic system),用于半自動(dòng)地構(gòu)建機(jī)器可檢查的證明。
圖 2 展示了一個(gè)簡(jiǎn)單的例子,以說(shuō)明定理是如何在 Lean 中被形式化和證明的:

策略(tactic)的語(yǔ)法是相當(dāng)靈活的,可以接受參數(shù),也可以組合成復(fù)合策略。策略可以看作是特定領(lǐng)域語(yǔ)言(DSL)中的程序。用戶可以通過(guò)定義新的策略來(lái)擴(kuò)展 DSL。這種離散的、組合的和無(wú)界的行為空間使得定理證明對(duì)機(jī)器學(xué)習(xí)具有挑戰(zhàn)性。
另一個(gè)挑戰(zhàn)是前提的選擇。前提是對(duì)證明一個(gè)定理有用的現(xiàn)有公理或定義,被用作策略的論據(jù)。證明不能使用尚未定義的前提,也不能使用未導(dǎo)入當(dāng)前文件的前提。通常,前提是來(lái)自一個(gè)包含數(shù)十萬(wàn)個(gè)現(xiàn)有定義和定理的大型數(shù)學(xué)庫(kù),這使得人類和機(jī)器都很難在生成策略時(shí)選擇正確的前提。這是定理證明中的一個(gè)關(guān)鍵瓶頸,也是研究者希望通過(guò)檢索增強(qiáng)的 LLM 來(lái)解決的。
LeanDojo Benchmark
研究者使用 LeanDojo 構(gòu)建了一個(gè)包含 96,962 條從 mathlib 提取的定理 / 證明的基準(zhǔn)。該基準(zhǔn)是目前最大的以數(shù)學(xué)為重點(diǎn)的定理證明數(shù)據(jù)集之一,涵蓋了不同的主題,如分析、代數(shù)和幾何。
與現(xiàn)有的 Lean 數(shù)據(jù)集不同,LeanDojo Benchmark 還包含了 128,163 個(gè)前提的定義,不僅包括定理,還包括可以作為前提的其他定義,例如圖 2 中的 gcd。此外,該數(shù)據(jù)集有 212,787 個(gè)策略,其中 126,058 個(gè)策略至少有一個(gè)前提。在有前提的策略中,前提的平均數(shù)量為 2.12。
LeanDojo Benchmark 解決了兩項(xiàng)關(guān)鍵問(wèn)題:
-
前提信息
Lean repos(例如,mathlib 或 lean-liquid)包含人寫(xiě)定理 / 證明的源代碼。然而,原始代碼并不適合用于訓(xùn)練驗(yàn)證器,它缺乏人類在使用 Lean 時(shí)可以獲得的運(yùn)行時(shí)信息,例如證明步驟之間的中間狀態(tài)。
而 LeanDojo 可以從 Lean 的任何 GitHub repo 中提取數(shù)據(jù),這些數(shù)據(jù)包含在原始 Lean 代碼中無(wú)法直接看到的豐富信息,包括文件依賴關(guān)系、抽象語(yǔ)法樹(shù)(AST)、證明狀態(tài)、策略和前提。LeanDojo Benchmark 包含細(xì)粒度的前提注釋(它們?cè)谧C明中使用的位置和在庫(kù)中定義的位置),為前提選擇提供有價(jià)值的數(shù)據(jù),也是定理證明的關(guān)鍵瓶頸。
-
具有挑戰(zhàn)性的數(shù)據(jù)分割
研究者發(fā)現(xiàn),將定理隨機(jī)分成訓(xùn)練 / 測(cè)試的常見(jiàn)做法導(dǎo)致了之前論文中高估了性能。LLM 只需在訓(xùn)練期間記住類似定理的證明,就能證明看似困難的定理。
在人類編寫(xiě)的 Lean 代碼中,一個(gè)常見(jiàn)的慣用語(yǔ)法是為同一數(shù)學(xué)概念的略微不同的屬性設(shè)置了一個(gè)類似的定理 / 證明塊。例如,在圖 3 中,最后兩個(gè)定理不僅看起來(lái)相似,而且有相同的證明。如果其中一個(gè)在訓(xùn)練中,模型可以通過(guò)記憶輕松證明另一個(gè)。這種捷徑使模型能夠證明看似不簡(jiǎn)單的定理,包括那些需要前提才能證明的定理。

在 LeanDojo Benchmark 中,研究者通過(guò)設(shè)計(jì)具有挑戰(zhàn)性的數(shù)據(jù)分割 novel_premises 來(lái)緩解這個(gè)問(wèn)題,它需要測(cè)試證明以使用至少一個(gè)從未在訓(xùn)練中使用過(guò)的前提。
例如,圖 3 中的最后兩個(gè)定理都使用了前提 conj_mul。如果一個(gè)定理在 novel_premises 分割的訓(xùn)練集中,另一個(gè)也必須在訓(xùn)練中。
以編程方式與 Lean 交互
LeanDojo 的另一個(gè)重要功能是以編程方式與 Lean 交互。它把 Lean 變成了一個(gè)類似健身房的環(huán)境,在這個(gè)環(huán)境中,證明器可以觀察證明狀態(tài),運(yùn)行策略來(lái)改變狀態(tài),并接收錯(cuò)誤或證明完成的反饋。這個(gè)環(huán)境對(duì)于評(píng)估 / 部署驗(yàn)證器或通過(guò) RL 訓(xùn)練證明器是不可缺少的。
下面是 LeanDojo 的主要形式,用于通過(guò)策略與 Lean 交互。Lean 同樣支持不基于策略的其他證明風(fēng)格,不過(guò) LeanDojo 只支持策略風(fēng)格的證明。但只要有足夠的通用性,任何證明都可以轉(zhuǎn)換為策略風(fēng)格的證明。
ReProver
隨后,研究者使用 LeanDojo Benchmark 來(lái)訓(xùn)練和評(píng)估了 ReProver。其核心是一個(gè)由檢索增強(qiáng)的策略生成器(圖 1 底部)。
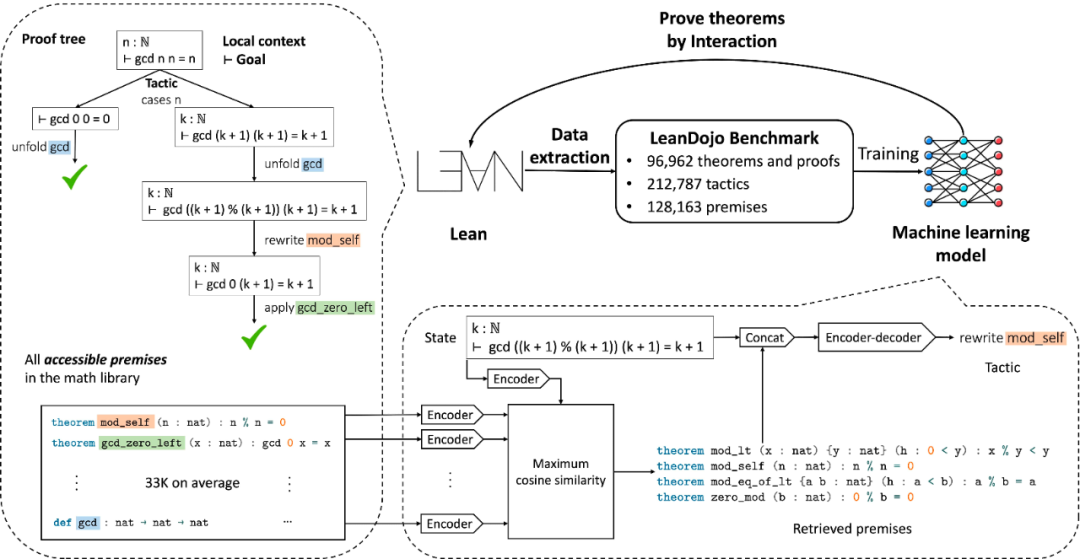
根據(jù)當(dāng)前的證明狀態(tài),它可以檢索出少數(shù)可能有用的前提,并根據(jù)狀態(tài)和檢索出的前提的連接情況生成一個(gè)策略。在證明定理時(shí),該模型在每一步都會(huì)生成多個(gè)策略候選者,這些候選者被用于標(biāo)準(zhǔn)的最優(yōu)搜索算法來(lái)尋找證明。
值得注意的是,ReProver 的訓(xùn)練只需要在單 GPU 上花費(fèi)五天時(shí)間(120 個(gè) GPU 時(shí)),所需的計(jì)算量大大低于之前的方法(1000 小時(shí)以上)。
此前的基于 LLM 的證明器都在數(shù)學(xué)和編碼的特定數(shù)據(jù)集上進(jìn)行預(yù)訓(xùn)練,計(jì)算成本很高而且數(shù)據(jù)集是保密的。相比之下,ReProver 避免特定領(lǐng)域的預(yù)訓(xùn)練,建立在「google/byt5-small」之上,這是一個(gè)通用的、公開(kāi)可用的、相對(duì)較小的模型檢查點(diǎn)。
此外,ReProver 只在人類寫(xiě)的策略上進(jìn)行了微調(diào),沒(méi)有輔助數(shù)據(jù)或通過(guò)與 Lean 在線互動(dòng)收集的數(shù)據(jù)。雖然這些正交方向是有價(jià)值的,但會(huì)大大增加方法的復(fù)雜性和計(jì)算要求。
在評(píng)估實(shí)驗(yàn)中,ReProver 可以證明 51.4% 的定理,優(yōu)于直接生成策略而不進(jìn)行檢索的 baseline(47.5%)和另一個(gè)使用 GPT-4 以零樣本方式生成策略的 baseline(28.8%)。

研究者還在 MiniF2F 和 ProofNet 兩個(gè)數(shù)據(jù)集上測(cè)試了 ReProver。它可以在 MiniF2F 中證明 26.5% 的定理,在 ProofNet 中證明 13.8% 的定理,這幾乎能夠媲美強(qiáng)化學(xué)習(xí)的 SOTA 方法,且訓(xùn)練時(shí)使用的資源少得多。
此外,許多定理在 Lean 中沒(méi)有 ground- truth 證明。而 ReProver 能夠證明 65 個(gè)目前在 Lean 中沒(méi)有得到證明的定理,其中 MiniF2F 發(fā)現(xiàn)了 33 條證明,ProofNet 中發(fā)現(xiàn)了 39 條。研究者表示,ReProver 也可以作為一個(gè)有效的工具來(lái)增強(qiáng) Lean 中現(xiàn)有的數(shù)學(xué)庫(kù)。
ChatGPT 插件
研究者還構(gòu)建了一個(gè) LeanDojo ChatGPT 插件,使 ChatGPT 能夠通過(guò)與 Lean 交互來(lái)證明定理。與專門針對(duì)定理證明進(jìn)行微調(diào)的 LLM(例如 ReProver)相比,ChatGPT 可以將非形式化數(shù)學(xué)與形式化證明步驟交織在一起,類似于人類與證明助手的交互方式。它可以解釋來(lái)自 Lean 的錯(cuò)誤消息,并且比專門的證明器更容易操縱。然而,由于搜索和規(guī)劃方面的弱點(diǎn),在大多數(shù)情況下很難找到正確的證明。
示例如下:
a + b + c = a + c + b
Stirling’s formula
Gauss' summation formula
團(tuán)隊(duì)信息
最后來(lái)認(rèn)識(shí)一下這篇文章的作者們:

論文一作楊凱峪目前是加州理工學(xué)院計(jì)算和數(shù)學(xué)科學(xué) (CMS) 系的博士后研究員 ,此前在普林斯頓大學(xué)獲得博士學(xué)位。
Alex Gu 是麻省理工學(xué)院的一名博士生,導(dǎo)師為 Armando Solar-Lezama。此前,他在麻省理工學(xué)院獲得了學(xué)士和碩士學(xué)位,擁有 Meta AI Research、Jane Street 和 pony.ai 多家公司的實(shí)習(xí)經(jīng)歷。
Peiyang Song 目前是加州大學(xué)圣巴巴拉分校(UCSB)創(chuàng)意研究學(xué)院(CCS)的計(jì)算機(jī)科學(xué)本科生。他的研究工作主要集中在兩個(gè)方向:1)神經(jīng)定理證明和自動(dòng)推理,結(jié)合大型語(yǔ)言模型(LLMs)和交互式定理證明器(ITPs);2)用于能源效率機(jī)器學(xué)習(xí)推理的時(shí)間邏輯。
Shixing Yu 目前是美國(guó)康奈爾大學(xué)計(jì)算機(jī)科學(xué)專業(yè)博士生,此前在德州大學(xué)奧斯汀分校獲碩士學(xué)位,本科就讀于北京大學(xué)信息科學(xué)技術(shù)學(xué)院。
參考鏈接:
https://unlocked.microsoft.com/ai-anthology/terence-tao/
https://unlocked.microsoft.com/ai-anthology/terence-tao/
THE END
原文標(biāo)題:大模型幫陶哲軒解題、證明數(shù)學(xué)定理:數(shù)學(xué)真要成為首個(gè)借助AI實(shí)現(xiàn)突破的學(xué)科了?
文章出處:【微信公眾號(hào):智能感知與物聯(lián)網(wǎng)技術(shù)研究所】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
-
物聯(lián)網(wǎng)
+關(guān)注
關(guān)注
2912文章
44877瀏覽量
375665
原文標(biāo)題:大模型幫陶哲軒解題、證明數(shù)學(xué)定理:數(shù)學(xué)真要成為首個(gè)借助AI實(shí)現(xiàn)突破的學(xué)科了?
文章出處:【微信號(hào):tyutcsplab,微信公眾號(hào):智能感知與物聯(lián)網(wǎng)技術(shù)研究所】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
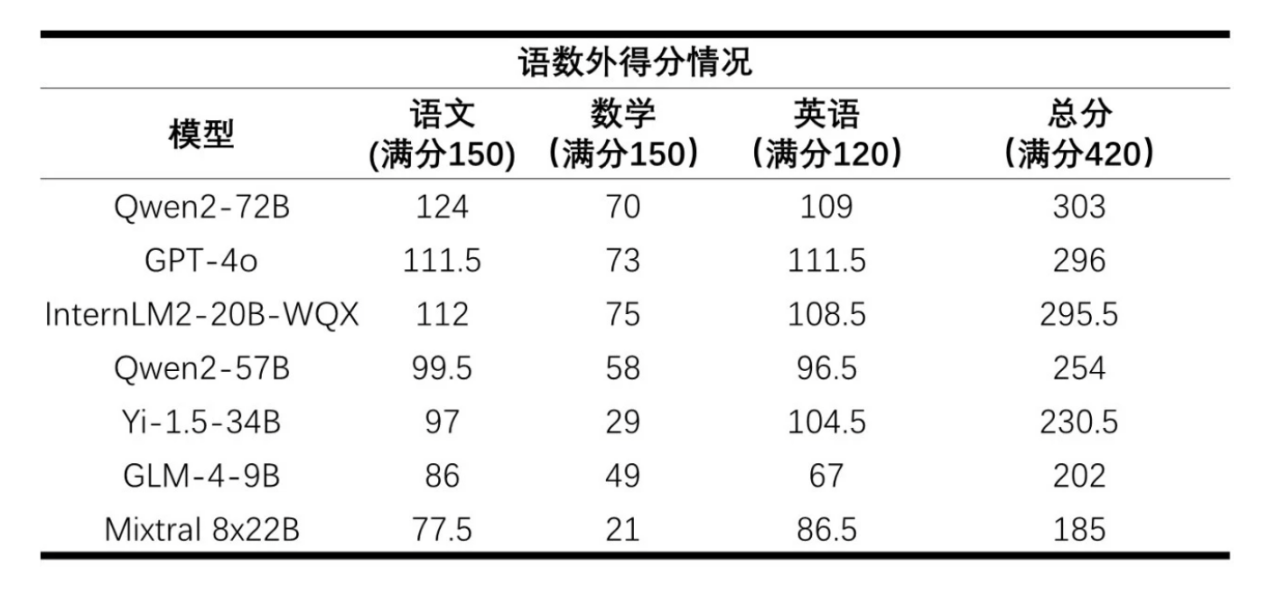
閉卷開(kāi)考全國(guó)一卷,AI大模型高考數(shù)學(xué)全部不及格?!
科大訊飛星火大模型升級(jí)發(fā)布會(huì)回顧
光電效應(yīng)的數(shù)學(xué)模型及解析
Kimi發(fā)布新一代數(shù)學(xué)推理模型k0-math
傅里葉變換的數(shù)學(xué)原理
阿里Qwen2-Math系列震撼發(fā)布,數(shù)學(xué)推理能力領(lǐng)跑全球
阿里云推出首個(gè)域名AI大模型應(yīng)用
神經(jīng)網(wǎng)絡(luò)反向傳播算法的原理、數(shù)學(xué)推導(dǎo)及實(shí)現(xiàn)步驟
數(shù)學(xué)建模神經(jīng)網(wǎng)絡(luò)模型的優(yōu)缺點(diǎn)有哪些
神經(jīng)網(wǎng)絡(luò)在數(shù)學(xué)建模中的應(yīng)用
當(dāng)AI與數(shù)學(xué)同時(shí)走下神壇

工業(yè)控制器的制作與數(shù)學(xué)的關(guān)系
Opera瀏覽器引領(lǐng)潮流,全球首接端側(cè)AI大模型
【大語(yǔ)言模型:原理與工程實(shí)踐】大語(yǔ)言模型的評(píng)測(cè)
三相SVPWM電壓型逆變器的數(shù)學(xué)模型




 大模型幫陶哲軒解題、證明數(shù)學(xué)定理:數(shù)學(xué)真要成為首個(gè)借助AI實(shí)現(xiàn)突破的學(xué)科了?
大模型幫陶哲軒解題、證明數(shù)學(xué)定理:數(shù)學(xué)真要成為首個(gè)借助AI實(shí)現(xiàn)突破的學(xué)科了?










評(píng)論