相平面法
前言
非線性系統(tǒng)的相平面法是一種分析和研究非線性系統(tǒng)動力學(xué)行為的方法。相平面法通過將系統(tǒng)的狀態(tài)變量表示為二維平面上的軌跡,來揭示非線性系統(tǒng)的穩(wěn)定性、周期性、吸引子等特性。
對于非線性系統(tǒng),其狀態(tài)變量的演化不再遵循簡單的線性關(guān)系。相平面法的基本思想是將非線性系統(tǒng)的動力學(xué)方程轉(zhuǎn)化成一組一階微分方程,并將其表示為相平面上的向量場。這樣,系統(tǒng)的狀態(tài)變量就可以在相平面上以軌跡的形式展示。
通過相平面法,可以觀察到系統(tǒng)在相平面上的軌跡的形狀和特性,從而推斷系統(tǒng)的穩(wěn)定性和行為。常見的特性包括平衡點(穩(wěn)定點)、極限環(huán)、吸引子等。通過分析軌跡的形狀、軌跡的相交點以及軌跡的變化趨勢,可以確定系統(tǒng)的穩(wěn)定性、周期性或者混沌行為。
相平面法也存在一些缺點需要考慮:
- 限于二維系統(tǒng):相平面法只適用于二維系統(tǒng),對于高維系統(tǒng)無法直接應(yīng)用。在高維系統(tǒng)中,相平面法無法提供完整的動力學(xué)行為描述,因為它無法展示高維空間中的復(fù)雜軌跡。
- 無法精確解析求解:相平面法主要是基于圖形觀察和分析,而不是通過解析計算得到精確解。因此,特別是對于非線性系統(tǒng)和復(fù)雜的微分方程,相平面法無法提供準(zhǔn)確的定量信息。
- 可視化有限:相平面法能夠提供關(guān)于系統(tǒng)行為的直觀圖像,但在大規(guī)模系統(tǒng)或長時間尺度上,圖像可能變得復(fù)雜且難以解釋。對于復(fù)雜的相軌跡和相平面,僅憑人眼可能無法完全捕捉到細(xì)微的變化和行為特征。
- 不能涵蓋所有情況:相平面法主要用于研究振蕩、穩(wěn)定性和周期性等特定系統(tǒng)行為。對于其他類型的非線性動力學(xué)行為,如混沌行為,相平面法可能無法提供全面的理解。
- 對數(shù)值求解的依賴:在實際應(yīng)用中,相平面法通常依賴于數(shù)值計算和數(shù)值模擬。這涉及到選擇適當(dāng)?shù)臄?shù)值方法,并且對數(shù)值誤差和數(shù)值穩(wěn)定性要有充分的認(rèn)識。
相平面


奇點
平衡點是使系統(tǒng)永久停駐的點,即


非線性系統(tǒng)的相平面分析
在奇點附近,相軌跡的特征與線性系統(tǒng)比較接近,因此可以通過進行非線性系統(tǒng)的線性化,然后進行分析。常用的方法是利用泰勒公式進行展開。泰勒公式是一個關(guān)于函數(shù)在某點附近的展開式,通過展開可以將非線性函數(shù)近似為線性函數(shù),從而方便進行局部分析。

極限環(huán)
奇線是相軌跡中的特殊情況,將相平面劃分為具有不同運動特性的區(qū)域。最常見的奇線是極限環(huán)。非線性系統(tǒng)會出現(xiàn)自振蕩,因此在相平面上會形成一條孤立的曲線,這條曲線附近的相軌跡會逐漸趨向或離開這條曲線,這就是極限環(huán)。
極限環(huán)將相平面分為內(nèi)部平面和外部平面兩部分,軌跡無法從極限環(huán)內(nèi)部穿過進入外部,反之亦然。這樣就將相平面劃分為具有不同運動特性的區(qū)域,因此,極限環(huán)也是相平面上的分界線,對于確定系統(tǒng)的全部運動狀態(tài)非常重要。
需要指出的是,并非相平面上的所有孤立曲線都是極限環(huán)。在無阻尼的線性二階系統(tǒng)中,由于沒有阻尼造成的能量損耗,相平面圖是一系列連續(xù)的閉合曲線,這些曲線并非極限環(huán),因為它們不是孤立的,在任何特定閉合曲線的鄰近仍然存在其他的曲線。而極限環(huán)是相互孤立的,在任何極限環(huán)的鄰近不可能有其他的極限環(huán)。極限環(huán)是非線性系統(tǒng)中獨有的現(xiàn)象,它僅在非保守系統(tǒng)中出現(xiàn)。這種周期運動的原因不在于系統(tǒng)無阻尼,而是系統(tǒng)的非線性特性,導(dǎo)致系統(tǒng)能量交替變化,因此可以從非周期性的能源中獲取能量,從而維持周期運動。
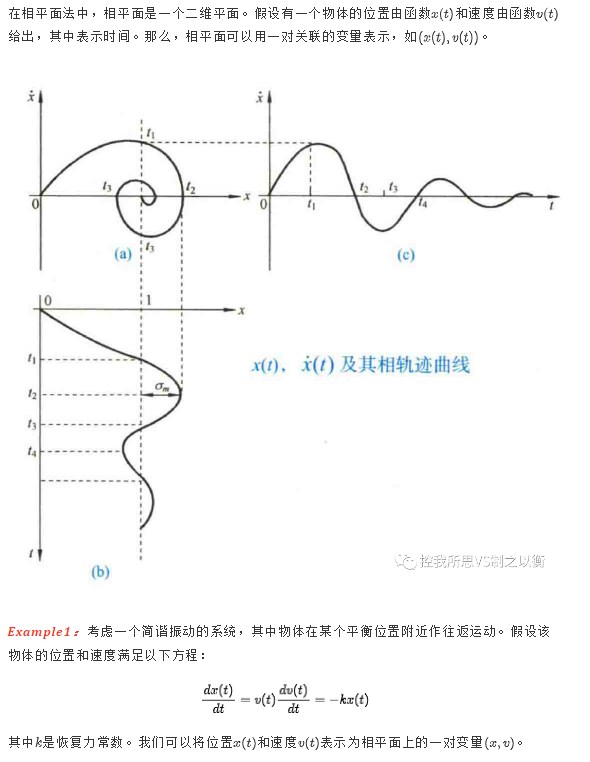
根據(jù)極限環(huán)附近相軌跡的運動特點,極限環(huán)可分為以下三種類型:
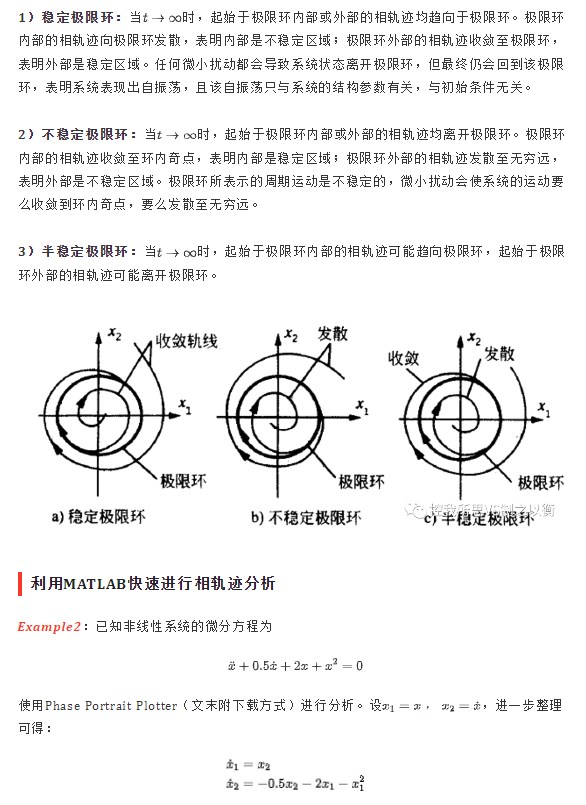
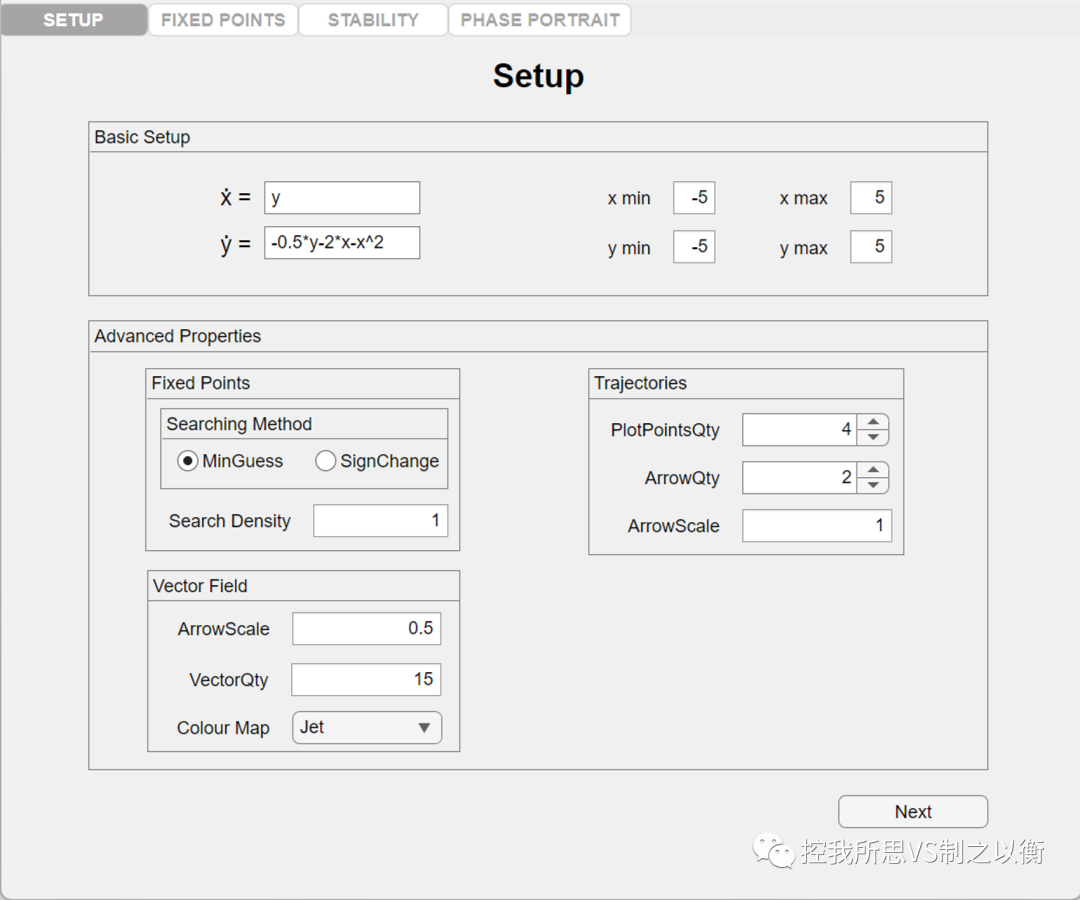
得出平衡點(奇點)

得到奇點類型
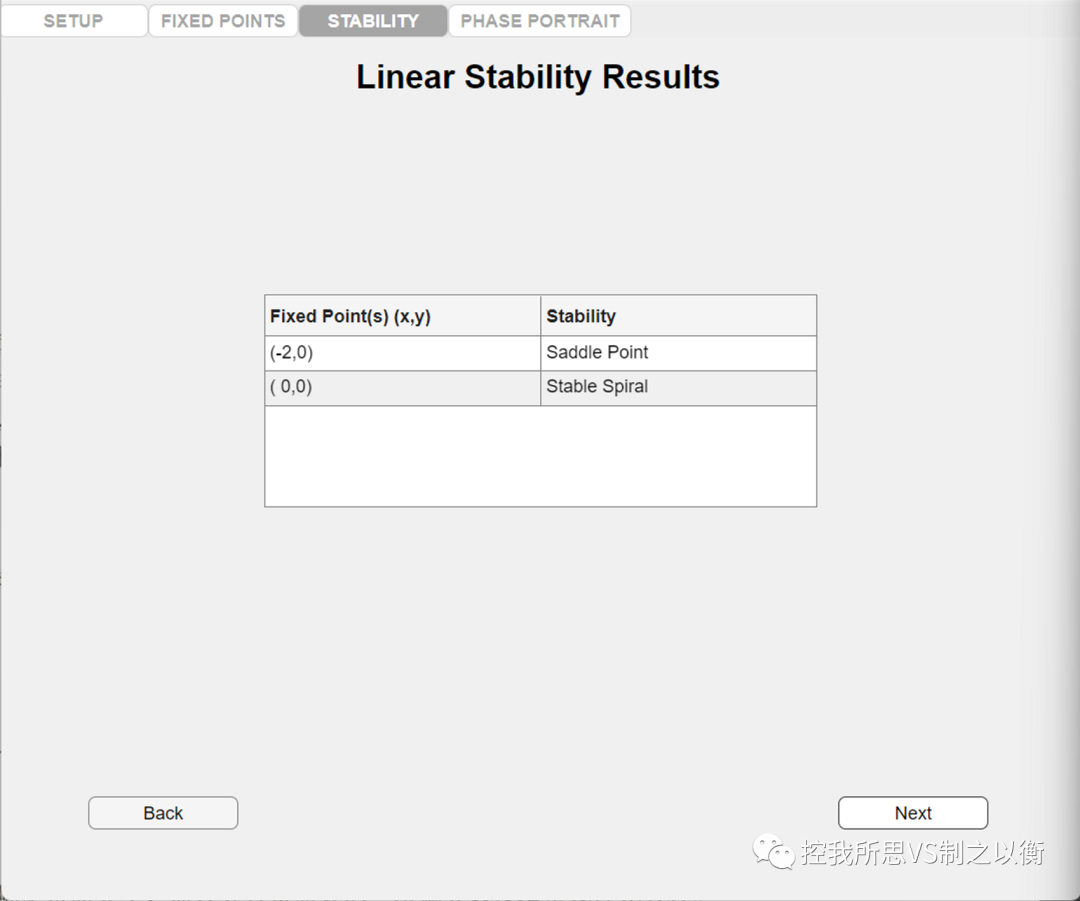
繪制相軌跡
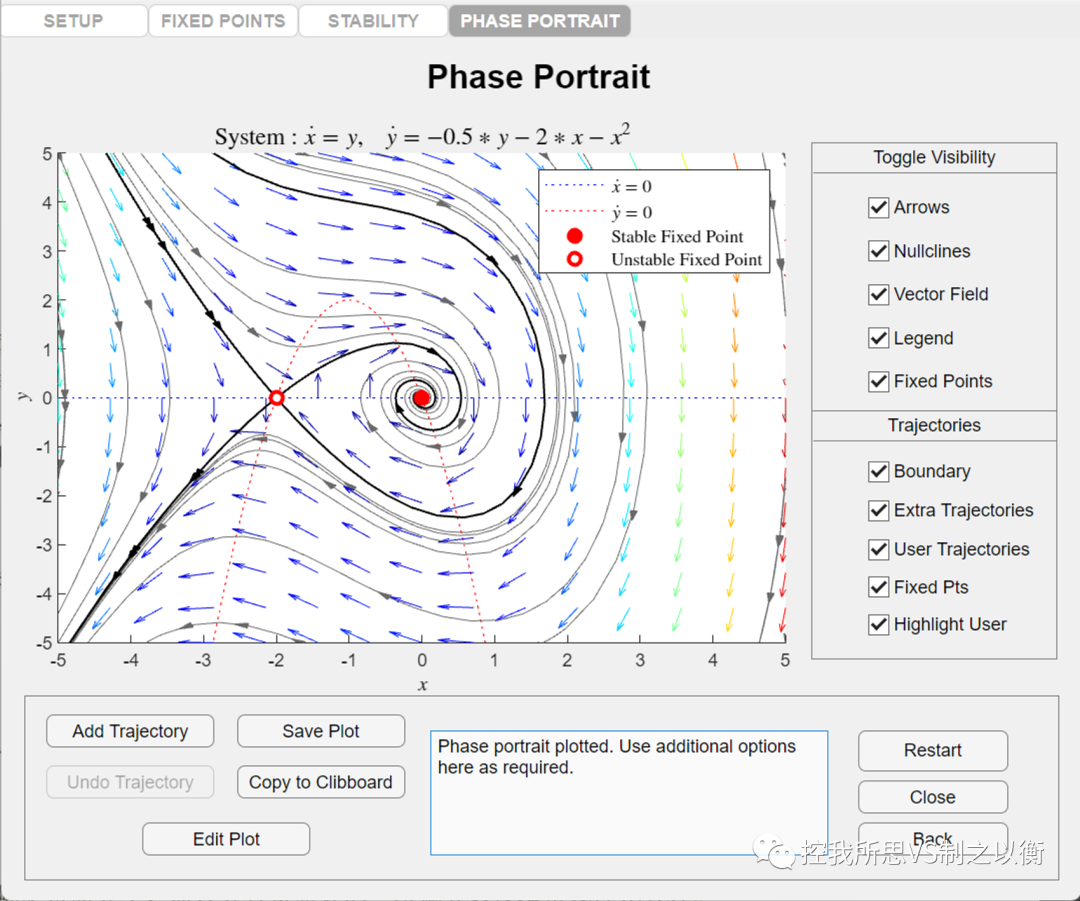
根據(jù)奇點的位置和類型,圖中與鞍點(-2,0)相交的兩條相軌跡可稱為奇線,將相平面劃分為兩個區(qū)域:系統(tǒng)的穩(wěn)定區(qū)域位于相平面圖中的內(nèi)區(qū)域,而不穩(wěn)定區(qū)域位于外區(qū)域。當(dāng)初始條件位于陰影線內(nèi)區(qū)域時,系統(tǒng)的運動將收斂至原點;當(dāng)初始條件位于陰影線外區(qū)域時,系統(tǒng)的運動將發(fā)散至無窮大。該例說明非線性系統(tǒng)的運動及其穩(wěn)定性與初始條件有關(guān)。
Example3 :已知帶死區(qū)特性的非線性系統(tǒng)的微分方程為
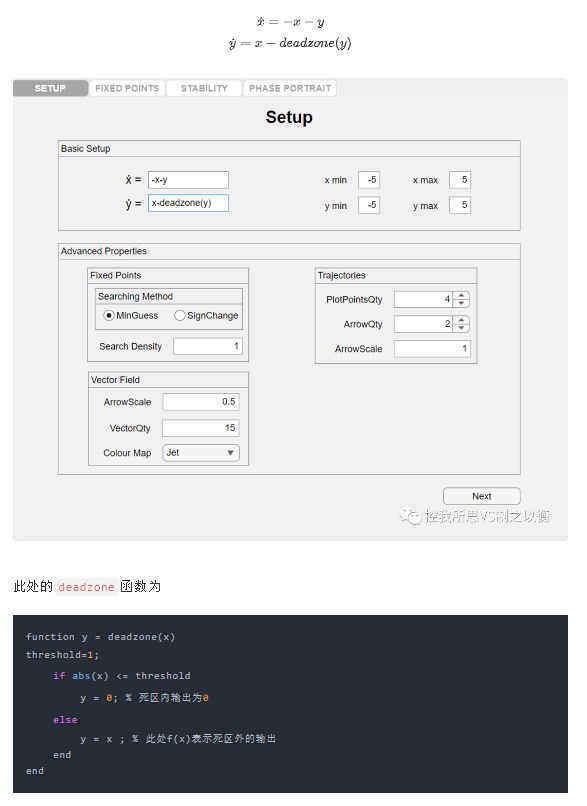
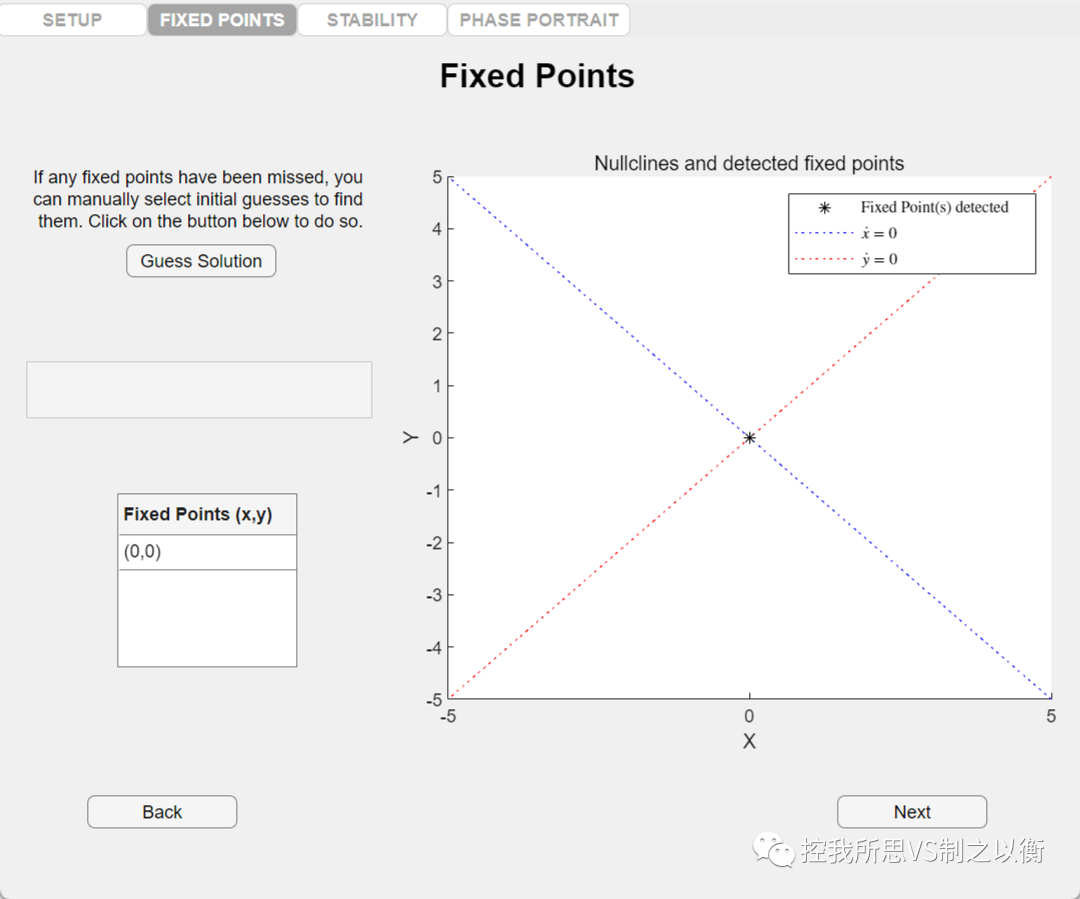
確定平衡點
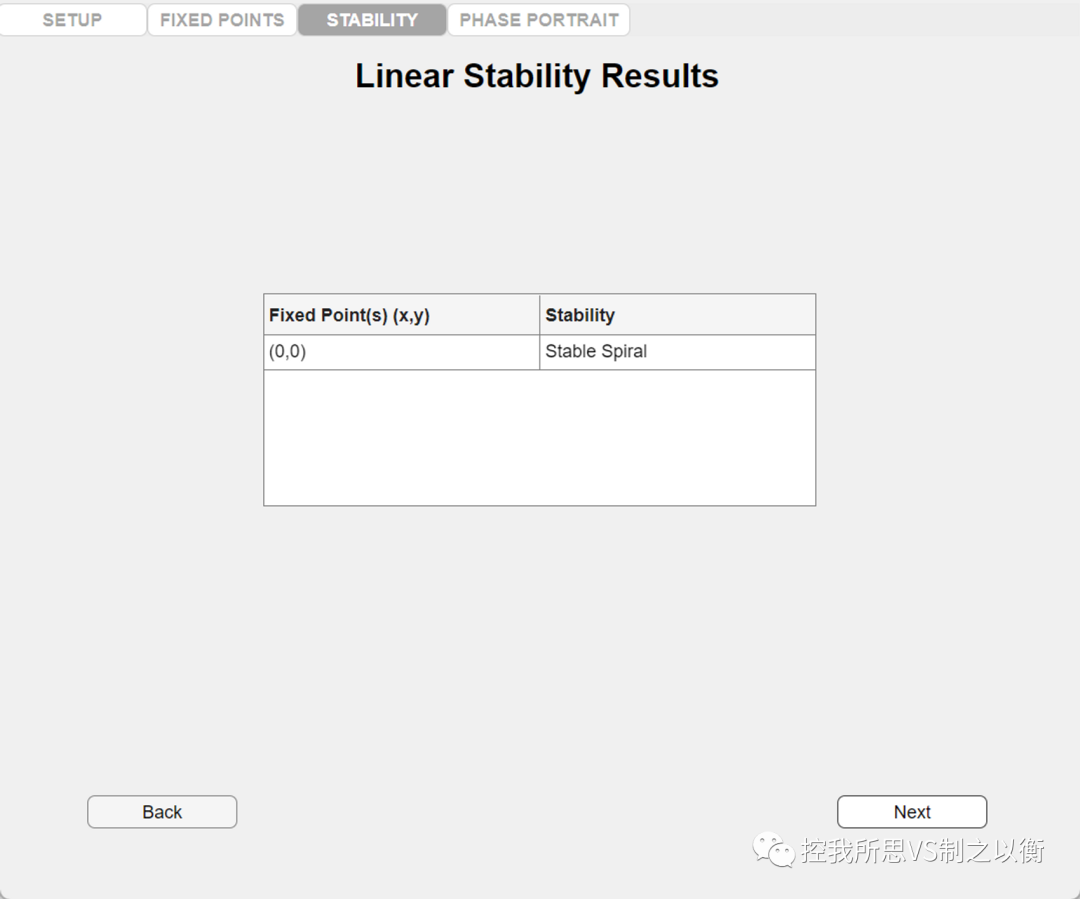
得到奇點類型
得到相軌跡

-
狀態(tài)機
+關(guān)注
關(guān)注
2文章
492瀏覽量
27615 -
MATLAB仿真
+關(guān)注
關(guān)注
4文章
176瀏覽量
19968 -
非線性系統(tǒng)
+關(guān)注
關(guān)注
0文章
20瀏覽量
7894 -
二階系統(tǒng)
+關(guān)注
關(guān)注
1文章
16瀏覽量
9601
發(fā)布評論請先 登錄
相關(guān)推薦
高階非線性控制系統(tǒng)相平面的實現(xiàn)
基于多模型的非線性系統(tǒng)廣義預(yù)測控制
基于正交小波網(wǎng)絡(luò)的非線性系統(tǒng)辨識
非線性系統(tǒng)輸出反饋控制
一種典型的非線性系統(tǒng)分析
非線性系統(tǒng)辨識
非線性系統(tǒng)辨識模糊模型參數(shù)收斂問題研究
自動控制系統(tǒng)教程之非線性系統(tǒng)分析的資料免費下載
何長安非線性系統(tǒng)控制理論的PDF電子書免費下載




 淺析非線性系統(tǒng)的相平面法
淺析非線性系統(tǒng)的相平面法

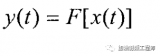










評論