前言
自從上世紀50年代以來,計算機視覺技術一直是學術界和工業界的熱點問題,尤其是近十年來,隨著新一輪人工智能技術的蓬勃發展,得到AI加持的計算機視覺技術快速走進了人們的日常生活,不斷重塑著人們的生活方式。
顧名思義,計算機視覺是指讓計算機能夠理解、分析和處理圖像和視頻的技術,通過研究高效的計算機算法和系統,使計算機獲得像人類一樣理解和使用視覺信息的能力。在這個過程中,人們需要綜合運用計算機科學、數學、物理學、生理學、心理學等跨學科的知識才能更好地解決一些實際問題。
隨著視覺應用場景的不斷擴大,越來越多的人已經認識到,相機成像技術處在一個十分關鍵的地位。在討論視覺算法的效能時,人們經常會引用一個經典的英語表述“garbage in,garbage out”,這是在說,如果相機采集的基礎圖像本身就沒有有用的信息,那么再復雜精妙的算法也不可能給出有用的結果。所以,作為愛芯元智的企業目標之一,就是不斷研發最前沿的AI-ISP技術,期望為視覺算法提供優質的輸入圖像,使上層應用能夠在各種高挑戰場景下保持穩定的性能輸出。
說到圖像質量,這其實是可以討論一千零一夜的話題,不過總的來說,人們會從分辨率、解像力、幀率、延遲、色彩還原、細節還原、噪聲、動態范圍、偽像、拖影、畸變等多個不同的維度分別對圖像質量進行量化分析,最終形成一個總的評價。在一類典型的應用場景中,視覺算法的核心任務是精確測量物體的形狀和距離,測得的參數將作為一系列重要決策的依據,有些決策可能關乎企業盈虧,而另一些決策則可能關乎人身安全。此時,輸入圖像的幾何畸變常常是影響系統性能的關鍵因素之一,為此人們發展出了一系列方法對圖像畸變進行分析和處理。
在這篇文章里,我們想分享的是人們在處理圖像幾何畸變問題時常用的思想方法和數學工具,希望相關的討論能夠對部分讀者有所啟發。本文所討論的部分技術已經集成在愛芯元智AX620系列芯片的標準軟件發布包中,可以幫助智慧城市、機器視覺等行業的用戶對廣角鏡頭進行畸變校正。另外,在智慧城市和輔助駕駛領域常見的雙攝、多攝拼接產品形態,其核心任務是對多個圖像進行像素級校正和融合,所以對鏡頭參數標定和畸變校正算法提出了更高的要求。在研究更高精度和收斂性的算法過程中,本文討論的方法和工具也會有所裨益。關于圖像拼接融合的技術架構已經在AX620和AX650系列芯片中得到了支持,關鍵算法和工具還在不斷優化完善中,歡迎感興趣的朋友關注。
1. 數學建模
與很多其它學科一樣,計算機視覺從業者在分析相機成像問題時,會首先建立一個關于相機系統成像原理的數學模型,簡稱相機模型(camera model)。一個最為基本且眾所周知的相機模型是小孔成像模型(pinhole model),其原理如圖1所示。
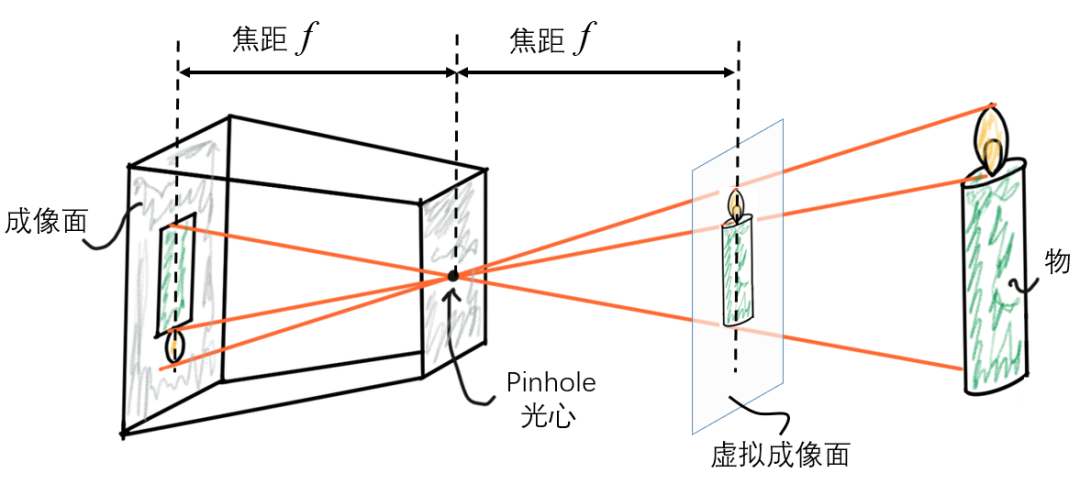
圖1 小孔成像模型(pinhole camera model)
這個模型假定光是沿直線傳播的,模型定義了一個特殊的點即光心,一個焦距參數,也就是成像面與光心之間的距離。通常會以光心為原點建立相機坐標系,并規定物方空間的Z坐標為正,像方空間的Z坐標為負。為了計算方便,模型還定義了虛擬成像面,虛擬成像面上的像是正立的,可以避免負號。
小孔成像模型的優點是足夠簡單,只需要初中數學的相似三角形知識就可以計算像的大小。當相機的視場角比較小時,小孔成像模型是相機成像過程的一個良好近似。但是當相機使用廣角鏡頭,或者應用場景對模型精度要求很高時,小孔成像模型就不夠準確了,此時必須在模型中引入成像畸變模型,使模型與實際情況更加符合。
在工程實踐中,人們經常需要用具體的數字來定義什么是大,什么是小,什么是成功,什么是失敗。在評價一個成像模型的精度時,人們會使用重投影誤差(reprojection error)指標作為參考。這個指標的含義是,假設物方空間中存在一個3D坐標點P,它被相機成像后,實際從圖像上提取到的2D坐標是p,此值包含了一切設計因素和隨機因素導致的誤差,如果再把P值代入相機成像模型進行計算,模型預測的2D坐標是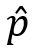 ,我們把p與
,我們把p與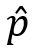 之間的像素距離定義為P點的重投影誤差。圖2顯示了重投影誤差的基本思想。
之間的像素距離定義為P點的重投影誤差。圖2顯示了重投影誤差的基本思想。
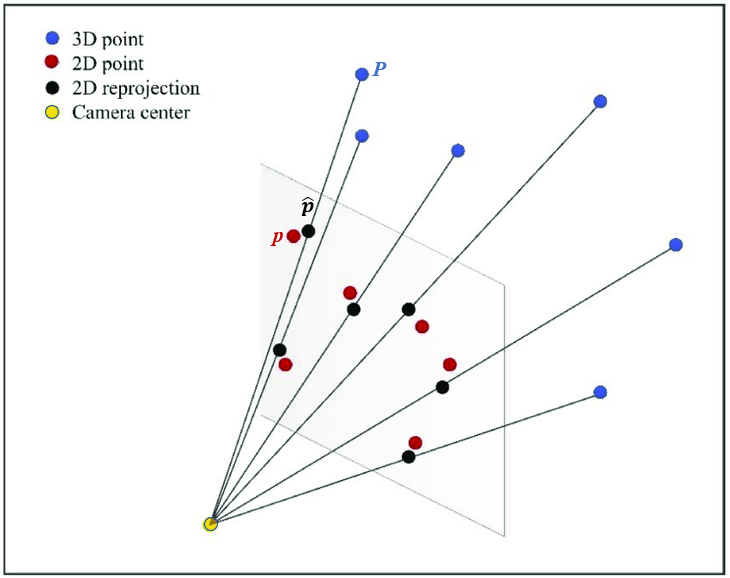
圖2 重投影誤差(reprojection error)
顯然,一張圖像中會包含成千上萬個與P點類似的點,如果只用一個點的誤差值來代表整張圖像那明顯是不太合適的。但是我們可以從一張圖像中篩選出一批有代表性的點,把這些點的重投影誤差的某種平均值作為成像模型的重投影誤差,這樣就比較公允了。進一步地,如果算法的輸入數據是一個視頻序列,那么只用一張圖像的誤差來代表整個序列也同樣是不太合適的,此時需要把每一張圖像的誤差都計算出來,然后考察整個序列的平均值和方差情況,這樣得到的數據就會更可信一些。圖3是使用Matlab工具繪制的一個圖像序列的重投影誤差,從圖中可以看到,重投影誤差的序列平均值是0.18個像素,對于很多應用而言這是一個相當優秀的值。另外,重投影誤差在圖像之間會存在一定幅度的波動,而波動的大小也反應了成像模型的穩定性。
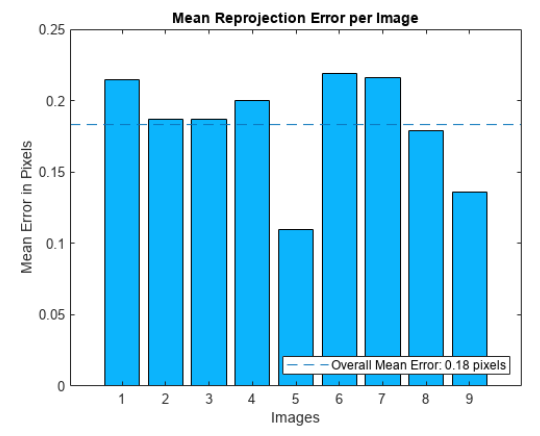
圖3 圖像序列的重投影誤差舉例
當我們掌握了重投影誤差這種評價方法之后,假設有一個新的成像模型擺在面前,我們就可以客觀地判斷這個模型是好是壞,是有競爭力還是缺乏競爭力。在很多時候,這個能力可以幫助我們規避錯誤決策的風險,讓我們總是站在一個相對安全的位置上。
回到剛才的話題,對于一個特定的相機系統,我們把偏離小孔成像模型的行為定義為一種畸變(distortion),當我們發現使用小孔成像模型得到的重投影誤差超出可接受標準時,此時就需要設計一個合適的數學模型來定量地描述畸變,然后根據畸變模型對原圖像進行校正,使校正圖像的重投影誤差收斂到可接受水平。
通過考察畸變行為我們能夠發現一些基本事實,首先,大部分的成像畸變都可以歸因于鏡頭的設計、制造、裝配等環節,因此通常可以用鏡頭畸變來指代成像畸變;其次,鏡頭畸變的特性和觀察尺度有關,在宏觀尺度上觀察時,廣角鏡頭和魚眼鏡頭通常表現為桶形畸變,長焦鏡頭經常表現為枕形畸變,這些行為是由鏡頭的光學設計決定的,每個鏡頭都應該具有相同的行為,而在微觀尺度上觀察時,鏡頭的某些局部區域會表現出相對宏觀規律的偏離,這往往是加工制造環節中一些不可控因素導致的,每個鏡頭的具體行為不一定相同;最后,不同生產批次的鏡頭,由于材料、加工、裝配等因素的變化,也會導致批次與批次之間呈現出可觀測的行為差異。
基于以上觀察我們認識到,鏡頭畸變模型可能需要分成兩類:如果應用場景對模型的精度要求不高,比如圖像主要是服務于人眼觀察,那么畸變模型只要能夠描述鏡頭的宏觀設計行為就可以了;如果應用場景對模型的精度要求很高,比如基于圖像進行測量的場景,那么畸變模型必須能夠描述鏡頭的局部特性,此類模型所使用的參數數量一定遠遠多于前者,獲取這些參數的過程也會更復雜。
對于描述鏡頭宏觀設計行為的畸變模型,我們不妨對問題做一些合理的簡化,首先假設鏡頭的行為是圓對稱的,只需要考察任一直徑方向上的成像規律,其次假設存在一條理想的光滑曲線可以精確地描述鏡頭的成像行為。基于這兩條假設,我們可以建立理想像點(基于小孔成像模型)與實際像點的函數關系r'=f(r),在某些情況下,我們可以把r作為理想像點,r'作為實際像點,在另一些情況下,也可以把r作為實際像點,r'作為理想像點。在r=0附近對光滑曲線f(r)做泰勒展開,并忽略階數高于N的余項,即可得到關于鏡頭實際成像公式的多項式模型:
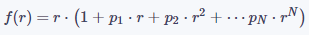
公式(1)
其中,r為理想像點(或實際像點)到鏡頭光心的距離,p1,?,pN是待定參數,需要通過實驗標定的方法獲得具體的值。
在實踐中,可以對(1)做進一步簡化,只使用其中的奇數次多項式或偶數次多項式,即:
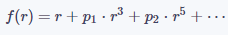
公式(2)
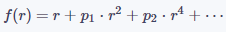
公式(3)
2. 優化問題
在前一節的討論中,我們已經能夠建立一個關于相機成像的數學模型,其中包含了鏡頭畸變的模型,但是該模型中存在一組待定系數p1,?,pN目前還不知道具體值,需要找到最優解。在數學上,這是一類典型的優化問題,已經有了很成熟的解決方案。實際上,早在1809年就出現了Gauss-Newton法來處理非線性最小二乘優化問題,但是該方法在迭代過程中要求目標函數的雅可比矩陣必須列滿秩,這一條件限制了它的應用。Levenberg于1944年提出了一個改進的方法,然后Marquardt在1963年進一步發展出了Levenberg-Marquardt方法,目前L-M方法已經成為非線性優化的首選方法。關于L-M方法的實現原理已有很多文獻給出了很好的描述,在OpenCV、Python、Matlab等工具中也提供了相應的庫可以直接調用,對此感興趣的讀者可以深入研究。
回到我們的具體問題,使用L-M方法求解鏡頭畸變模型的待定系數的過程是,首先要選定一組樣本G作為訓練集,假設G中包含m個樣本點。然后,定義變量x=(p1,?,pN)T,表示模型的待定參數;定義函數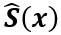 ,表示待定參數為x時,樣本G對應的模型預測值,該函數返回一個包含m個2D點坐標的向量;定義函數S(x),表示從圖像中提取的關于樣本G的實測值,同理,該函數返回一個包含m個2D點坐標的向量;
,表示待定參數為x時,樣本G對應的模型預測值,該函數返回一個包含m個2D點坐標的向量;定義函數S(x),表示從圖像中提取的關于樣本G的實測值,同理,該函數返回一個包含m個2D點坐標的向量;
定義重投影誤差函數:
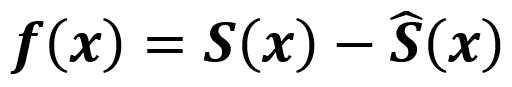
定義優化的目標函數:
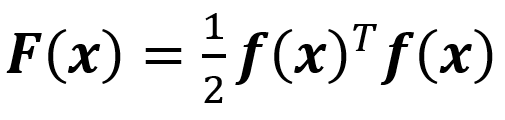
當x取最優解x*時,F(x*)取最小值。
此外,我們還需要手動提供一個x的初值x0,作為迭代優化的起始點。
在每一次迭代過程中,L-M算法會計算函數f(x)的雅可比矩陣J,然后根據公式(4)計算下一個x點距離當前點的步長?xlm,
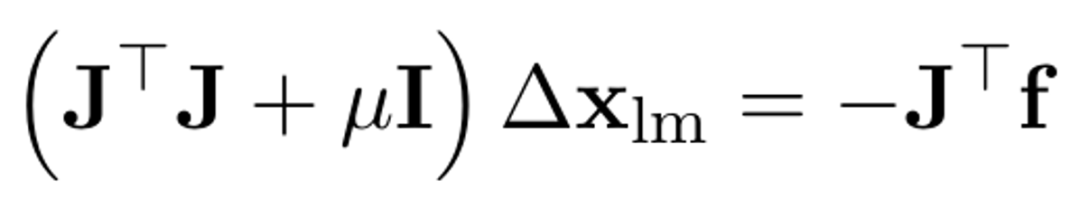
公式(4)
其中,μ≥0是一個阻尼因子,用于動態地調整?xlm的步長。
為了方便討論,我們先給出LM算法的偽代碼,然后簡要地討論一下其中涉及到的數學工具,期望起到拋磚引玉的作用。

觀察上述偽代碼可知,LM算法的關鍵在于如何求解線性方程組(A+μI)h=g,其中h是由待定參數構成的向量,系數矩陣A=J(x)TJ(x)是一個n階方陣,它的元素是對傳感器圖像運行某種特征提取算法得到的,比如圖4所示的例子,是使用Matlab軟件從相機拍攝的棋盤格圖像中提取角點的位置坐標。

圖4 使用Matlab工具提取棋盤格特征點
由于圖卡不平整、曝光不均勻、軟件四舍五入等隨機因素的存在,矩陣A的元素值包含了多種誤差的貢獻,因此本質上并不存在一個“絕對正確的h”,我們只能希望得到一個“較好的h”。一般而言,參與計算的樣本越多,離群樣本的貢獻就越小,得到的結果就越優。接下來的問題是,如何求解h向量才能獲得最佳的數值精度和穩定性,因為不同的方法在特性上是有一定區別的。在實踐中,我們經常會使用三種方法來求解線性方程組。
我們假定矩陣A的維度為nxn,h為n維列向量,包含n個待定的參數,I為n維單位矩陣,J或J(x)為mxn的雅克比矩陣。為了求解n個未知數,數學上必須有m≥n,否則這是一個欠定問題,h有無窮多解。當然,我們已經知道樣本點是越多越好,所以m≥n本來也是在計劃之內的。
進一步地,我們記y=f(x)為m維列向量,記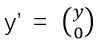 為(m+n)維列向量。另外,我們定義
為(m+n)維列向量。另外,我們定義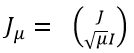 是一個分塊矩陣,其維度為 m’xn,m’ = (m+n)。借助以上定義,我們可以把兩個矩陣相加等價地表示成兩個矩陣相乘,即:
是一個分塊矩陣,其維度為 m’xn,m’ = (m+n)。借助以上定義,我們可以把兩個矩陣相加等價地表示成兩個矩陣相乘,即:
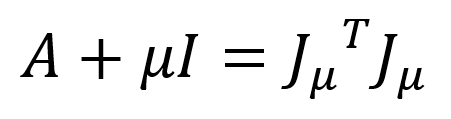
公式(5)
其中,上標T代表矩陣的轉置操作。
我們馬上會發現,使用兩個矩陣相乘的表示方法會給我們帶來很多便利。
方法一,Cholesky分解
對矩陣(A+μI)進行Cholesky分解,即:A+μI=RTR,其中I為單位陣,R為上三角矩陣。注意到矩陣A= J(x)TJ(x)+μI為正定矩陣,則R的對角元素為正。我們得到 RTRh=g,則利用兩次“回代”即可求出h。
Cholesky分解計算速度很快,所以使用較為廣泛,但該方法存在較大的計算誤差。深入研究發現,Cholesky分解的誤差正比于矩陣(A+μI)的條件數+,而它又等于矩陣Jμ條件數的平方。因此為減少數值計算的誤差,我們的計算對象應該是Jμ而不是(A+μI)。
+矩陣的條件數
矩陣的條件數(condition number)是數值分析和線性代數中的一個重要概念,任意矩陣B的條件數為σmax /σmin,其中,σmax表示B的最大奇異值,σmin表示B的最小奇異值。條件數刻畫了矩陣令向量發生形變的能力。條件數越大,向量在變換后可能的變化量就越大,而大的條件數會放大數據中存在的誤差。關于條件數的介紹可參考書籍:Matrix Analysis-Roger A. Horn -2nd Edition
方法二 QR分解
我們注意到,方程(A+μI)h=g=-JTy,這是一個線性最小二乘問題,即min||Jμh+y'||2的正規方程(關于h的梯度等于0的方程),則求解該方程等價于求對應線性二乘問題的解。
我們對矩陣Jμ進行QR分解得到:Jμ?P=QR=Q1R1,其中,Q是維度為m’xm的單位正交矩陣,R為m’xn維的上三角矩陣;Q1為Q的前n列,維度為m’xn;R1為R的前n行,維度為nxn;P為列變換基本矩陣,使得R的對角線元素的絕對值遞減(即|Rii|≥|Rjj|,i<j),其維度為nxn。
將該QR分解等式帶入線性最小二乘的式中化簡可知,R1PTh=-Q1Ty',然后利用回代法,即可得到h。
QR分解法的計算誤差正比于矩陣Jμ的條件數,而不是該矩陣條件數的平方,所以它比Cholesky分解更穩定,但會增加計算量。當優化變量的維度較小時,QR分解法使用比較廣泛,實際上很多流行的最優化庫(比如minpack和ceres)都是基于QR分解實現的。
方法三SVD分解
將矩陣Jμ進行SVD分解,即:Jμ=USVT=U1S1VT,其中:U為m’xm’維的單位正交陣;S為m’xn維的對角陣;V為nxn維的單位正交陣;U1為U的前n列,維度為m’xn;S1為S的前n行,維度為nxn;將SVD分解等式帶入線性最小二乘的式中并化簡,可知:
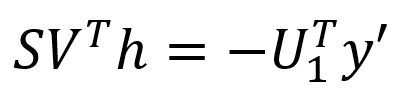
簡單整理可得下方公式,即可計算出h。
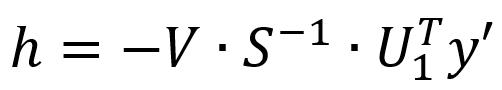
SVD法的穩定性很高,但其計算量也最大。
以上我們討論了求解LM算法核心方程組時三種常用方法的優缺點。另外我們也注意到,以L-M算法為代表的非線性優化方法并不能保證總是給出收斂的解,其收斂與否往往與我們手動提供的初值質量有關。在工程領域,一個不保證總是有效的方案其可用性是大打折扣的,必須要有其它機制作為失效后的補充。因此,一個十分重要的研究課題是尋找一些穩定可靠的線性優化方法,一方面為主算法提供一個良好的迭代初值,另一方面可以作為主算法失效時的備選方案。限于篇幅,本文對此就不做展開討論了,如果讀者喜歡,后續可以專題討論一下這個問題。
小結
在本文中,我們主要討論了計算機視覺領域經常遇到的一個基礎性問題,即如何定量地評價圖像的幾何畸變,以及如何通過數學建模的方法為鏡頭建立成像模型,從而能夠定量地描述成像畸變并加以校正。當鏡頭模型建立后,為了求解模型中的待定參數,我們還介紹了L-M方法,這是一種非常實用的最小二乘非線性優化方法,在工程技術領域有著非常廣泛的應用。雖然很多文獻和資料都會有涉及LM算法的應用,但是討論LM算法實現細節的資料卻頗為少見,所以我們借本文簡要討論了求解LM算法可以使用的數學工具以及工具背后的數理邏輯,希望我們所討論的這些思想方法和具體工具能對讀者帶來一定的啟發,非常感謝廣大讀者對愛芯元智的關注和支持,我們下期再會!
審核編輯:湯梓紅
-
計算機
+關注
關注
19文章
7534瀏覽量
88476 -
相機
+關注
關注
4文章
1367瀏覽量
53825 -
AI
+關注
關注
87文章
31490瀏覽量
269979 -
人工智能
+關注
關注
1795文章
47642瀏覽量
239769 -
視覺技術
+關注
關注
0文章
87瀏覽量
13529
原文標題:愛芯分享 | 淺談相機成像問題中的數學工具
文章出處:【微信號:愛芯元智AXERA,微信公眾號:愛芯元智AXERA】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
Matlab符號數學工具箱應用說明
相機成像不產生拖影的曝光時間計算
數碼相機譜線成像技術探索
數碼相機的成像原理圖
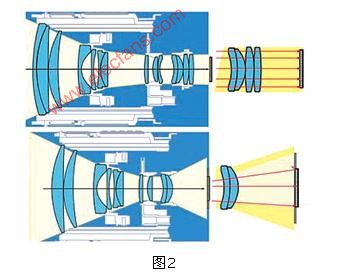
單反相機成像原理圖
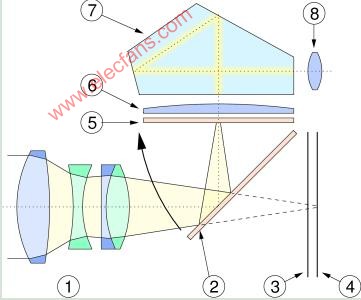
一種用于形狀精確描述的數學工具




 淺談相機成像問題中的數學工具
淺談相機成像問題中的數學工具












評論