濾波是頻域范疇,它說的是不同頻率的信號經過一個電路處理后,信號發生變化的問題,變化包含了原始信號幅值和相位的變化,濾波電路對信號的幅值做出的響應稱為幅頻響應,對信號相位做出的反應稱為相頻響應。每一個頻率的信號對應在時域就是信號的充放電特性。
濾波通常借助動態器件如電感和電容,利用它們在不同頻率下阻抗變化,從而在其上面產生壓降,對我們需要去除的信號進行衰減,從而達到濾波的效果。
我們知道電感和電容的阻抗特性其實就是儲能特性,儲能意味著時間特性,需要過程,這個過程是濾波特性的體現的一方面。
2、分析方法和工具
在s域,寫出回路的傳遞函數,根據波特圖進行分析,傳遞函數是輸入和輸出的增益關系
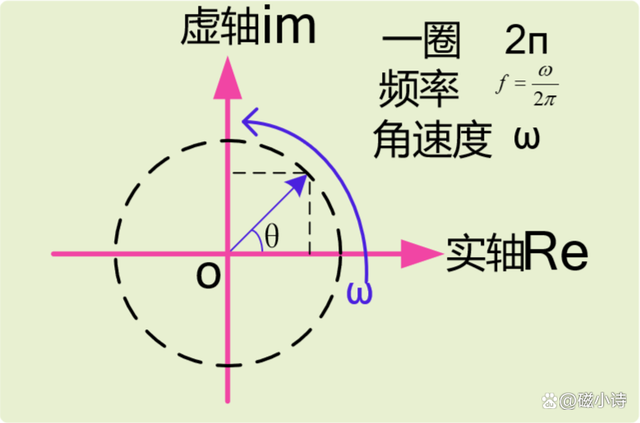
為了同時分析相位和幅值引入虛數,并且在虛平面進行分析,和頻率相關的電路阻值特性,我們用阻抗描述,通常包含實部與虛部,這個數學工具的引入,包含了幅值和相位信息的體現,簡化了分析難度。
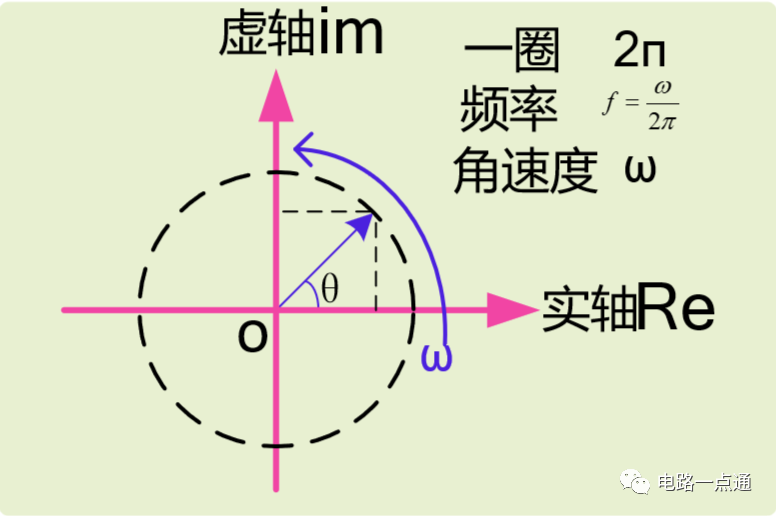
角速度描述表示
注:
由于自然界正弦信號認為是單一頻率的信號,是基礎信號,不可再分解,其它信號是以正弦為基礎的合成信號,所以,以下從電路輸入某個頻率的正弦信號開始分析。正弦信號輸入這些線性電路,達到穩定后,輸出信號只會發生幅值和相位的改變,不改變信號的頻率。
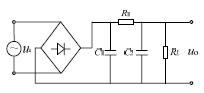
3、RC低通濾波電路結構和特性
(1)RC濾波電路,圖中包含了這個電路的傳遞函數G(s)表達式
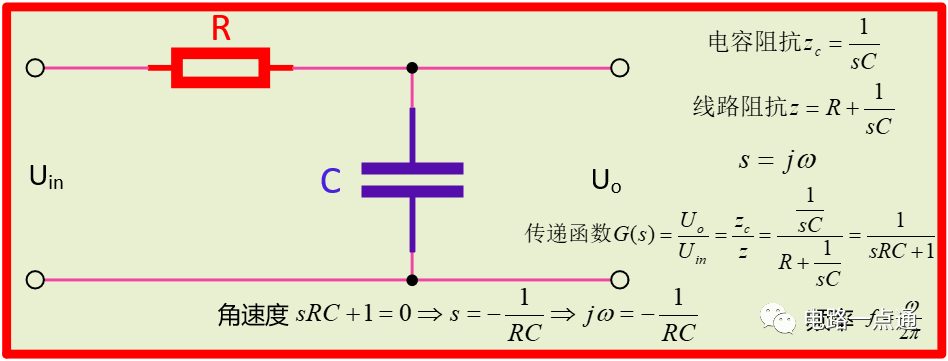
RC濾波電路
從傳遞函數解出一個稱作為極點的根,即令傳遞函數的分母為零,最后得出一個頻率,由于這個頻率從波特圖上看,曲線在這個點前后發生突變的現象,我們形象地將這個頻率稱為“轉折頻率”,轉折頻率意味著一個響應發生“突變”的頻率點,轉折意味著響應的轉彎點,前后會發生較大的變化。記住波特圖圖橫軸是頻率,代表著一系列不同頻率信號通過這個電路后,輸出會發生不一樣的變化,是一系列的信號,不是單一信號。轉折頻率代表了電路的固有特性,是電路參數和結構導致的結果,是電路的固有屬性。
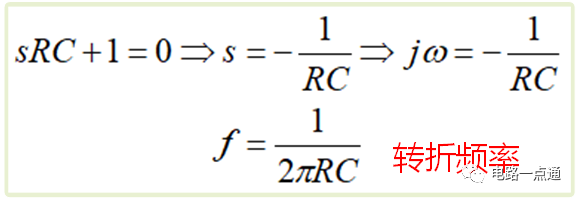
RC的轉折頻率
借助matalab工具進行繪制響應曲線,其它工具也可以,只要是自己熟悉的工具即可
**下面我們對R和C賦值,R=100Ω,C1=100uF,得到轉折頻率f=15.915Hz**
syms s R C % 定義符號參量
R=100; C=100*10^-6; % 給分子分母賦值
G(s)=1/(sRC+1); % 傳遞函數表達式
num=[0,1]; % 分子系數 den=[1/100,1]; % 分母系數
G1=tf(num,den)% 得出傳遞函數
margin(G1)% 畫出增益和相位裕量圖
grid on; % 得出傳遞函數為G(s)=1/(s/100 + 1)
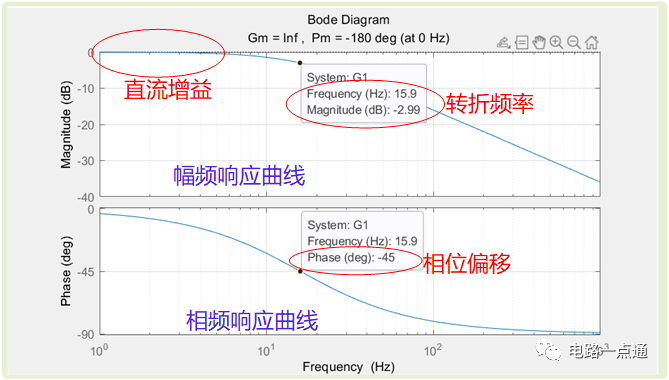
RC的幅頻和相頻曲線
曲線說明
(1)直流增益,即低頻增益,在傳遞函數中令s=0,得到直流增益為1,轉換成dB剛好為0dB(0dB=20log1),這正是我們無源器件低通濾波器的特點,不能放大信號,在低頻段,電容容抗幾乎為無窮大,即電容為開路狀態,信號被原模原樣傳輸過來,這時候增益就是1,由于電容看做開路 ,那么阻性電路中,信號自然也不會產生任何相位偏移。
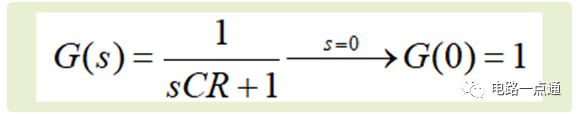
直流增益
(2)轉折頻率的地方,這個頻率的信號增益被衰減到原來的70.7%,也就是-3dB的地方,圖中為-2.99dB對應轉折頻率為15.9Hz,這是由于實際計算轉折頻率為15.915Hz,存在一點誤差。 對相位來說,在這個頻率點,相位會偏移-45°,負號表示信號被滯后了,從時間看,也就是被延時了。 但是對其它不同頻率信號在這個頻率點前后響應出現較大的不同。 之前看做不衰減也就是直流增益部分,之后信號被快速衰減,同時產生一定的相移。
(3)延時時間計算,也就是相位延遲和具體時間的對應關系,方便我們理解相位和延遲之間的關系,延遲時間為:延遲時間=Kd*周期
延遲系數Kd,即在一個360°周期里延遲角度占有的比例,這里是45/360=1/8,也就是45°占有360°的1/8。
轉折頻率約為15.9Hz,即一個周期為62.89ms。
那么,輸入信號被延時時間為62.89ms*1/8=7.86ms,輸出信號晚來輸入信號7.86ms。
如下是對一個100Hz和200Hz信號進行延時舉例,也說明了相位差和時間差之間的關聯,它們一一對應(one to one)
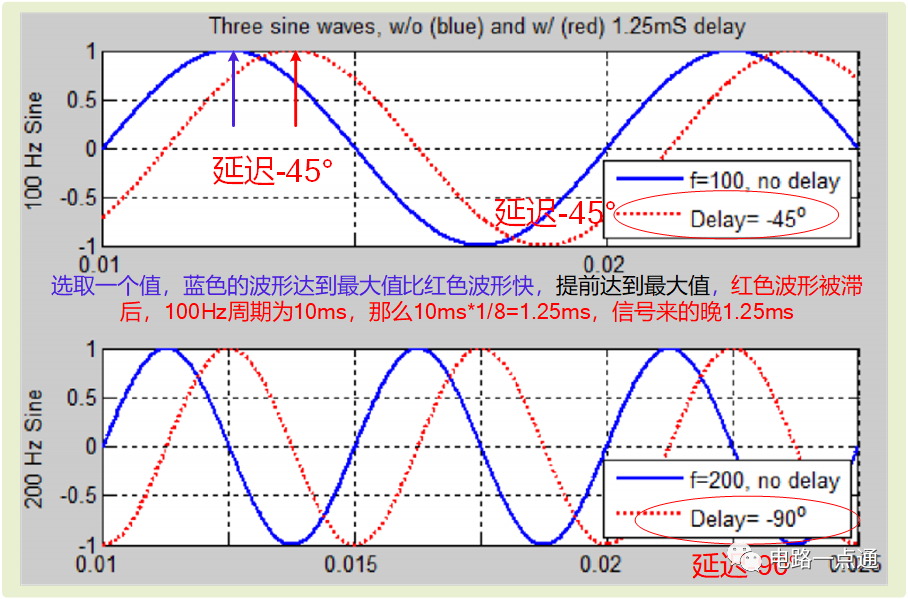
相位延遲的含義表示
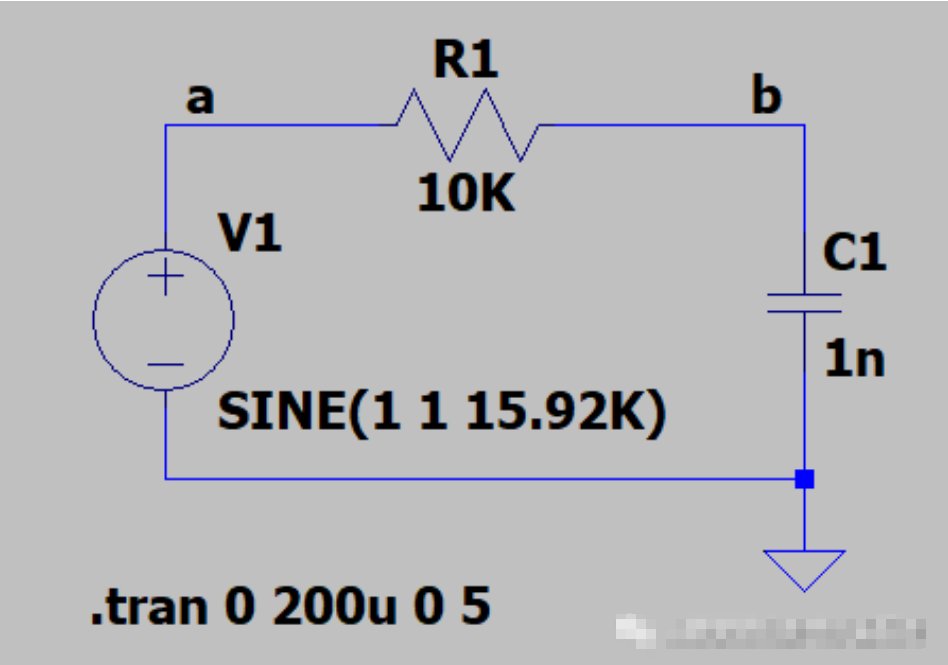
用TINA仿真進行波形驗證,借助仿真軟件驗證你的結果,并且可以幫助你理解
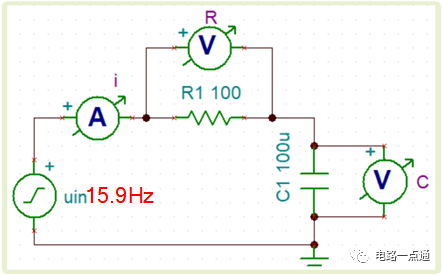
RC仿真電路
相比于輸入信號Uin,穩態后,電容電壓為輸出信號被滯后45°,并且幅度被衰減到70.7%,從下圖波形也可以看出。 (穩態后,電阻上電壓超前了45°,想象一下,這個電路測量對象不同,帶來了“高通”和“低通”的概念)
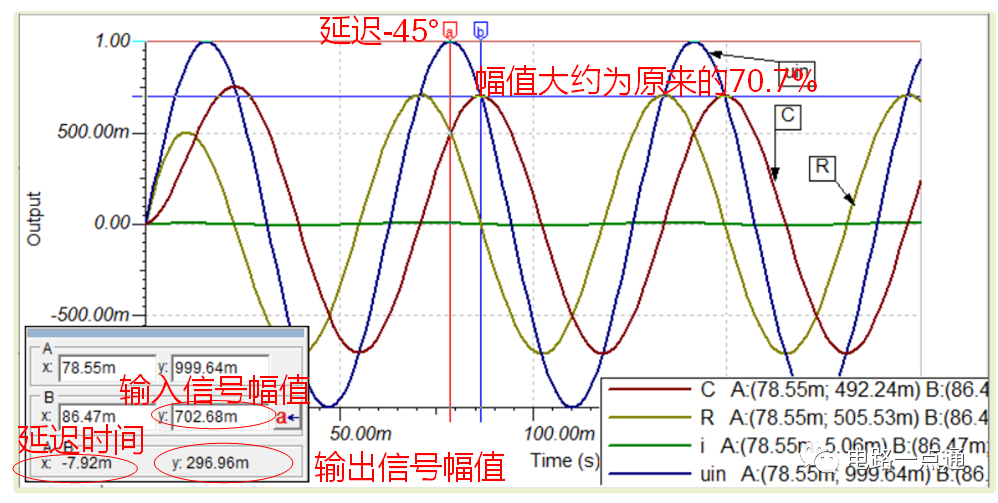
仿真波形
欄4、直接帶載后會發生什么?
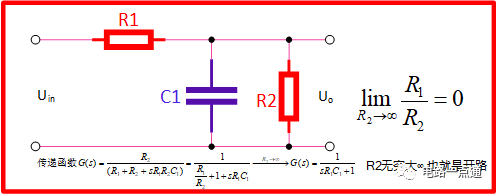
如下圖,我們將R2放置在電路中,模擬一個負載
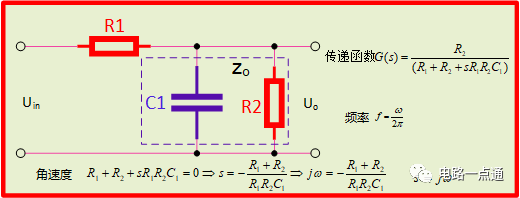
帶載的RC電路
我們再次借助MATLAB化簡方程
%zo輸出阻抗,是電容C1和電阻R2的并聯值 % z是電路總阻抗 % G(s)傳遞函數
符號 R1 R2 C1
zo=R2/(sC1R2+1);z=R1+zo;
G(s)=zo/z;G1(s)=simplify(G(s))%化簡代數式
最后得出傳遞函數為G(s)=G1(s)=R2/(R1 + R2 + C1R1R2*s)
同時令傳遞函數的分母為零解出極點,如上圖,我們可以把它寫作為頻率的形式,這個頻率在波特圖中正好是轉折頻率,我們利用MATLAB進行驗證
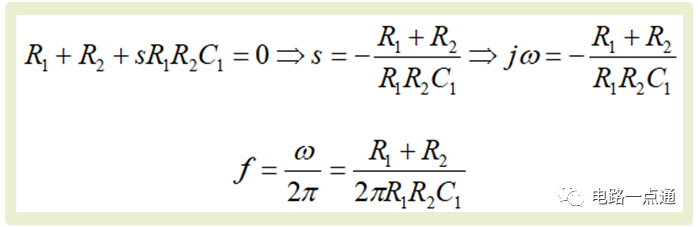
帶載后RC電路的轉折頻率
轉折頻率處,輸出信號相比輸入信號,輸入信號的幅值被衰減到原來的70.7%,相位被滯后45°(圖中就是-45,符號表示信號相位被滯后)
**下面我們對R1、R2和C1賦值,R1=100Ω、R2=20Ω,C1=100nF**
符號 R1 R2 C1 s
R1=100;R2=20;C1=100*10^-9;
zo=R2/(sC1R2+1);z=R1+zo;
G(s)=from/z;
G1(s)=simplify(G(s))%化簡代數式
% G(s)=G1(s)=R2/(R1 + R2 + C1R1R2*s)
%得到傳遞函數表達式 G(s)=G1(s)=100000/(s+600000)
num=[0.100000];den=[1.600000];
G1=tf(num,den)% 得到傳遞函數
保證金(G1)
網格打開;
最終得到幅頻和相頻特性圖
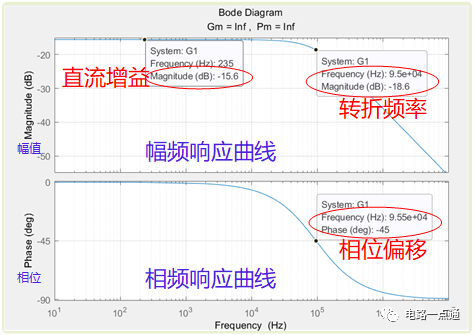
幅頻和相頻特性圖
(1)直流增益,也就是低頻下的增益,我們對傳遞函數頻率項s=0,那么就得到直流增益,這也是我們在做電源環路中分析中采取的方法得到直流增益。 這里直流增益如下,也就是除去了時效性動態器件的影響,純阻性表現的特性,就是一個簡單的分壓電路。
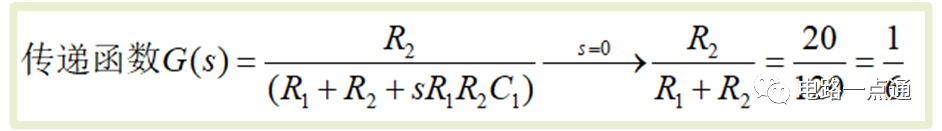
直流增益
注:1/6剛好是-15.6dB,負分貝表示信號被衰減
(2)轉折頻率處,我們經過簡單計算,得到轉折頻率為f=95.49kHz,如下圖,轉折頻率處信號衰減到原來的70.7%,即1/6*70%=0.1178,即為-18.6dB,波特圖中可以看出,同時相位被滯后45°(-45℃)。
這個電路,我們對并聯在C1上的R2取值為無限大,我們將R2取值無窮大后,只需要把傳遞函數簡單化簡后求極限,則電路重回到開頭的RC電路,傳遞函數和RC低通電路相同。
轉折頻率
注:負載的直接接入導致轉折頻率會向右移,即轉折頻率比單純的RC會偏高,若R2趨于∞,那么轉折頻率由95.49k變為15.92k(用Excel快速計算一下)。
實際中濾波電路該怎么樣接負載
實際當中,尤其是采樣電路,我們經常會用到RC低通濾波,我們會采用輸入阻抗很大的運放組成跟隨器。
在MCU中,采樣輸入端口往往也是阻抗很大,所以我們也可以直接用RC濾波進行直接接入
高輸入阻抗端口,這些都是讓我們想要的信號幅值不發生衰減,而且幾乎不產生相移、設定的轉折頻率不發生偏移,信號能夠被正常采集。
-
mcu
+關注
關注
146文章
17316瀏覽量
352237 -
濾波電路
+關注
關注
46文章
639瀏覽量
69776 -
頻率
+關注
關注
4文章
1534瀏覽量
59324 -
信號
+關注
關注
11文章
2804瀏覽量
77007 -
RC
+關注
關注
0文章
228瀏覽量
48913
原文標題:RC低通濾波電路:直接帶載對電路特性造成的影響
文章出處:【微信號:電路一點通,微信公眾號:電路一點通】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
談談直接帶載對RC低通濾波電路特性造成的影響
RC低通濾波電路的結構和特性




 RC低通濾波電路:直接帶載對電路特性造成的影響
RC低通濾波電路:直接帶載對電路特性造成的影響










評論