在之前的內容中,我們已經介紹過流水線并行、數據并行(DP,DDP和ZeRO)。今天我們將要介紹最重要,也是目前基于Transformer做大模型預訓練最基本的并行范式:來自NVIDIA的張量模型并行(TP)。它的基本思想就是把模型的參數縱向切開,放到不同的GPU上進行獨立計算,然后再做聚合。
在寫這篇文章的過程中,我發現要理解Megatron的大框架不難,但是涉及到細節,特別是混合并行部分,要考慮的就很多了。所以我去看了Megatron的源碼,在此基礎上配合圖例寫了這篇文章,其中的很多設計思想和細節就來自對源碼的閱讀。既然看都看了,因此我決定在大模型系列的下一章里,和大家一起閱讀Megatron的源碼,畢竟手動并行不像調API那樣簡單,需要根據實際模型設計并行框架,并知道在哪里打日志,做checkpoint。
如果對Transformer的設計不了解也沒關系,在這篇文章里都會給出圖解介紹,不過還是建議大家在閱讀前可先看以下文章:
Transformer學習筆記二:self-attention
圖解大模型系列之:數據并行上篇(DP與DDP),這篇中對AllReduce通信有詳細講解。
全文結構如下:
一、切分權重的兩種方法
二、MLP層
三、self-attention層
四、Embedding層
五、Cross-entropy層
六、經典并行:TP + DP (Megatron + ZeRO)
七、實驗效果與GPU利用率
八、參考
最后,Megatron,變形金剛反派隊伍霸天虎首領,現任環球影城脫口秀演員(啊不是),沒有它就沒有凸顯不出擎天柱們的戰績,沒有它就沒有變形金剛電影,我曾經的暑假快樂就要少很多。而現在沒有它就沒有大Transformer的誕生。所以,引燃人類AGI的熱情,可以被當作Megatron的陰謀拍進下一部電影里么?
一、切分權重
設輸入數據為X,參數為W。X的維度 = (b, s, h),W的維度 = (h, h')。其中:
b:batch_size,表示批量大小
s:sequence_length,表示輸入序列的長度
h:hidden_size,表示每個token向量的維度。
h':參數W的hidden_size。
則每次forward的過程如下:
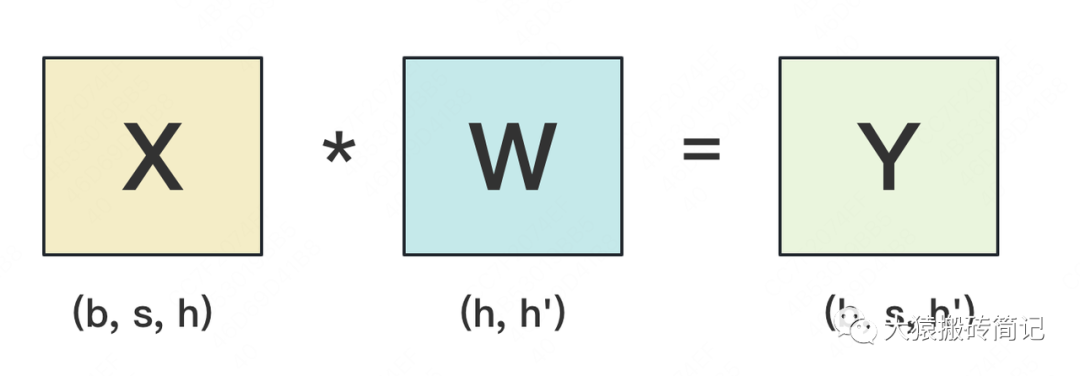
為畫圖方便,圖中所繪是b=1時的情況。假設現在W太大,導致單卡裝不下。我們需要把W切開放到不同的卡上,則我們面臨三個主要問題:
怎么切分W。
切完W后,怎么做forward。
做完forward后,怎么做backward,進而求出梯度,更新權重。一般來說,我們可以沿著W的行(h維度),或者列(h'維度)切分W。下面我們分別介紹這兩種切割辦法,并說明它們是如何做forward和backward的。
1.1 按行切分權重
(1) forward
我們用N來表示GPU的數量。有幾塊GPU,就把W按行維度切成幾份。下圖展示了N=2時的切割方式:
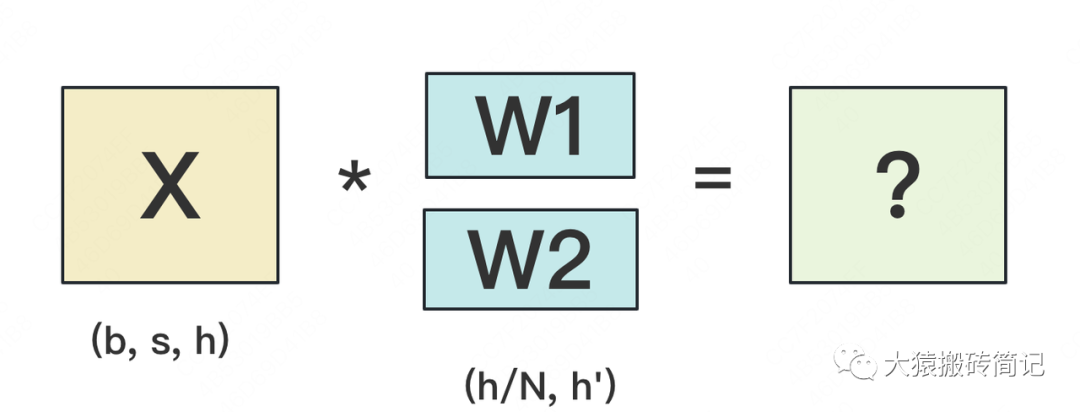
W按照行維度切開后,X的維度和它不對齊了,這可怎么做矩陣乘法呢?很簡單,再把X“按列切開”就行了,如下圖所示:
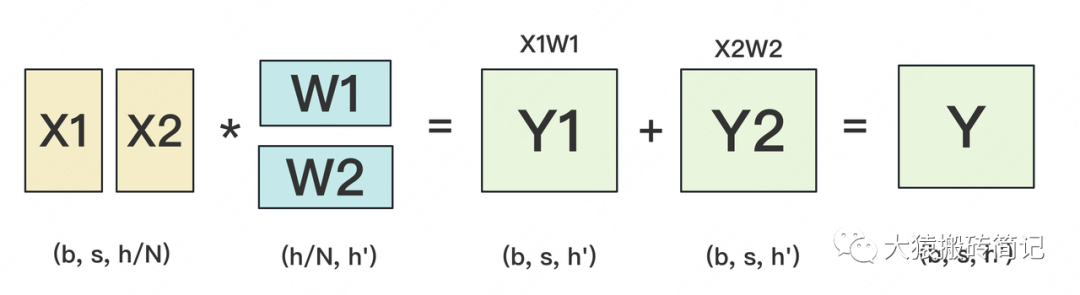
(2) backward
做完forward,取得預測值Y,進而可計算出損失L,接下來就能做backward了。我們重畫一下forward的過程,并在其中加入backward的部分,整體流程圖如下:
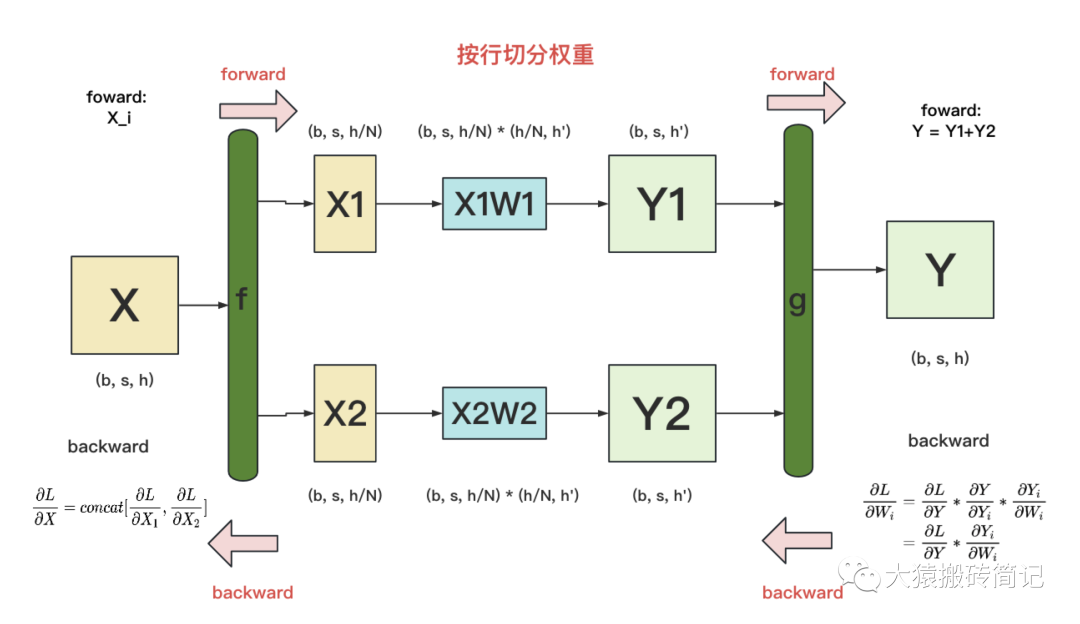
f 和 g:分別表示兩個算子,每個算子都包含一組forward + backward操作。forward操作已講過,不再贅述。
圖中的每一行,表示單獨在一塊GPU上計算的過程
g 的backward:假定現在我們要對求梯度,則可推出,也就是說,只要把同時廣播到兩塊GPU上,兩塊GPU就可以獨立計算各自權重的梯度了。
f 的backward:在上圖中,我們只畫了模型其中一層的計算過程。當模型存在多層時,梯度要從上一層向下一層傳播。比如圖中,梯度要先傳播到X,然后才能往下一層繼續傳遞。這就是f 的backward的作用。這里也易推出,
1.2 按列切分權重
(1)forward
按列切分權重后,forward計算圖如下:
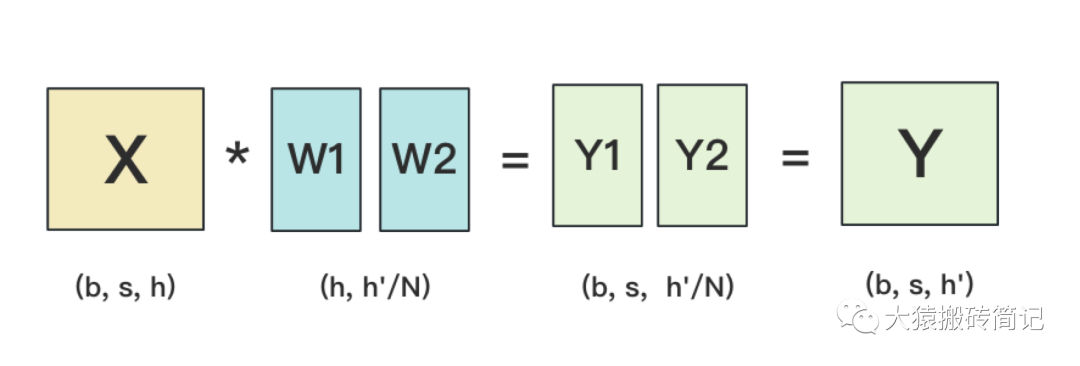
(2)backward
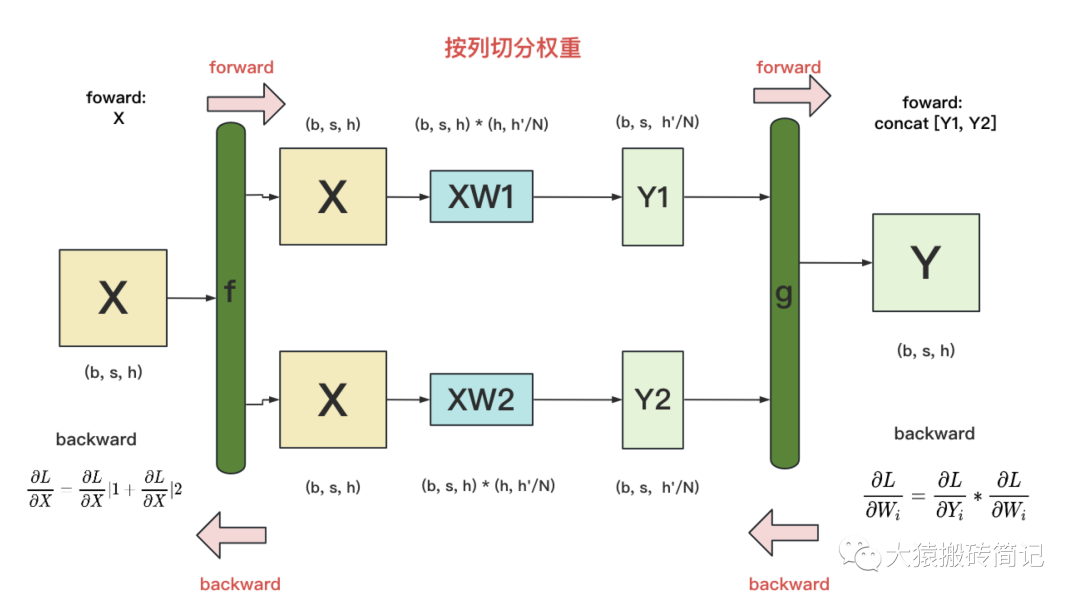
g的backward:易推出
f 的backward:因為對于損失L,X既參與了XW1的計算,也參與了XW2的計算。因此有。其中表示第i塊GPU上計算到X時的梯度。
現在,我們已分別介紹完了“按行”和“按列”切分權重的方法。在Megatron-LM中,權重的切分操作就是由這兩個基礎算子組合而成的。接下來,針對Transformer模型,我們依次來看在不同的部分里,Megatron-LM是怎么做切分的。
二、MLP層
2.1 MLP層的張量模型并行計算方法
MLP層構造最簡單,所以我們先來看它。MLP層計算過程如下圖:
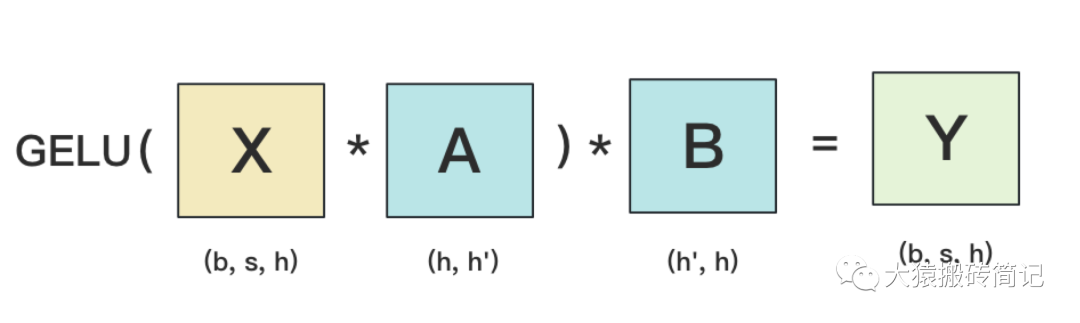
其中,GELU是激活函數,A和B分別為兩個線性層。在Transformer里,一般設h' = 4h。假設現在有N塊GPU,我們要把MLP層的權重拆到上面做計算,要怎么拆分呢?Megatron提供的拆分辦法如下:
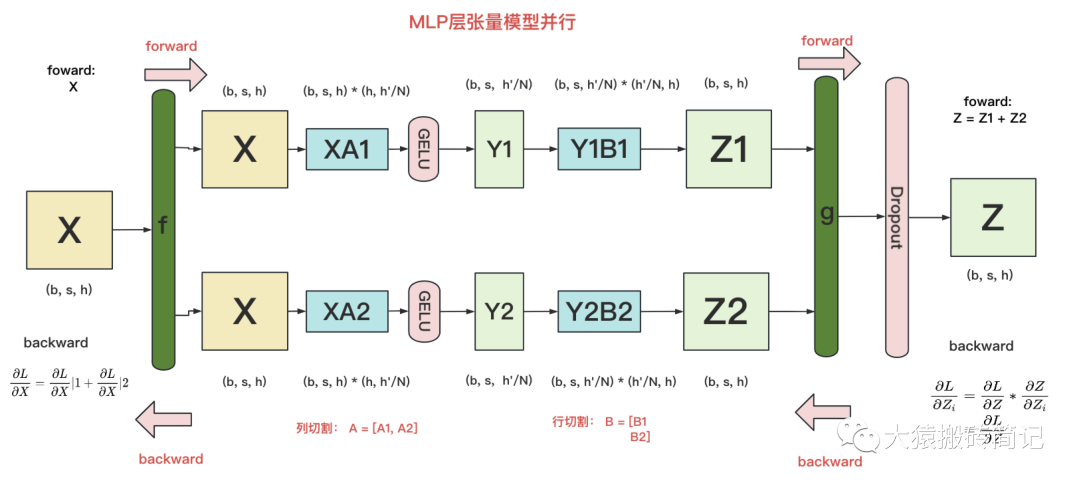
在MLP層中,對A采用“列切割”,對B采用“行切割”。
f的forward計算:把輸入X拷貝到兩塊GPU上,每塊GPU即可獨立做forward計算。
g的forward計算:每塊GPU上的forward的計算完畢,取得Z1和Z2后,GPU間做一次AllReduce,相加結果產生Z。
g的backward計算:只需要把拷貝到兩塊GPU上,兩塊GPU就能各自獨立做梯度計算。
f的backward計算:當當前層的梯度計算完畢,需要傳遞到下一層繼續做梯度計算時,我們需要求得。則此時兩塊GPU做一次AllReduce,把各自的梯度和相加即可。
為什么我們對A采用列切割,對B采用行切割呢?這樣設計的原因是,我們盡量保證各GPU上的計算相互獨立,減少通訊量。對A來說,需要做一次GELU的計算,而GELU函數是非線形的,它的性質如下:
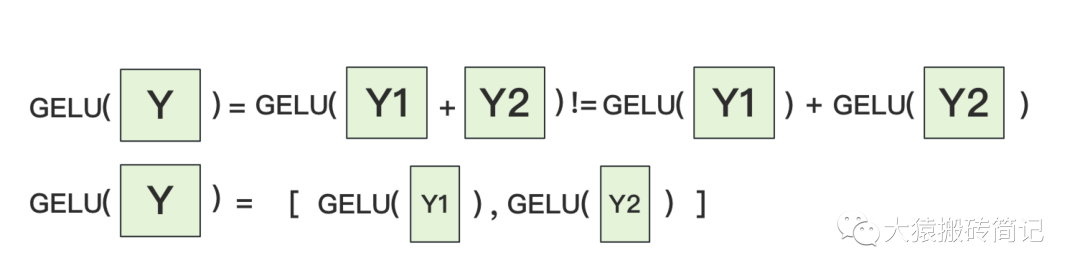
也就意味著,如果對A采用行切割,我們必須在做GELU前,做一次AllReduce,這樣就會產生額外通訊量。但是如果對A采用列切割,那每塊GPU就可以繼續獨立計算了。一旦確認好A做列切割,那么也就相應定好B需要做行切割了。
2.2 MLP層的通訊量分析
由2.1的分析可知,MLP層做forward時產生一次AllReduce,做backward時產生一次AllReduce。在之前的文章里我們講過,AllReduce的過程分為兩個階段,Reduce-Scatter和All-Gather,每個階段的通訊量都相等。現在我們設每個階段的通訊量為,則一次AllReduce產生的通訊量為。MLP層的總通訊量為。
根據上面的計算圖,我們也易知,
三、Self-Attention層
現在,我們來看稍微復雜一點的self-attention層切割方式(Transformer中Encode和Decoder之間還有做cross-attention,但計算邏輯和self-attention一致,因此這里只拿self-attention舉例)。
首先,我們快速過一下multi-head attention層的參數構造。對Transformer Attention不熟悉的讀者,可以參見之前寫的這篇文章,其中有詳細的圖解。
3.1Multihead-Attention的計算方法
當head數量為1時,self-attention層的計算方法如下:
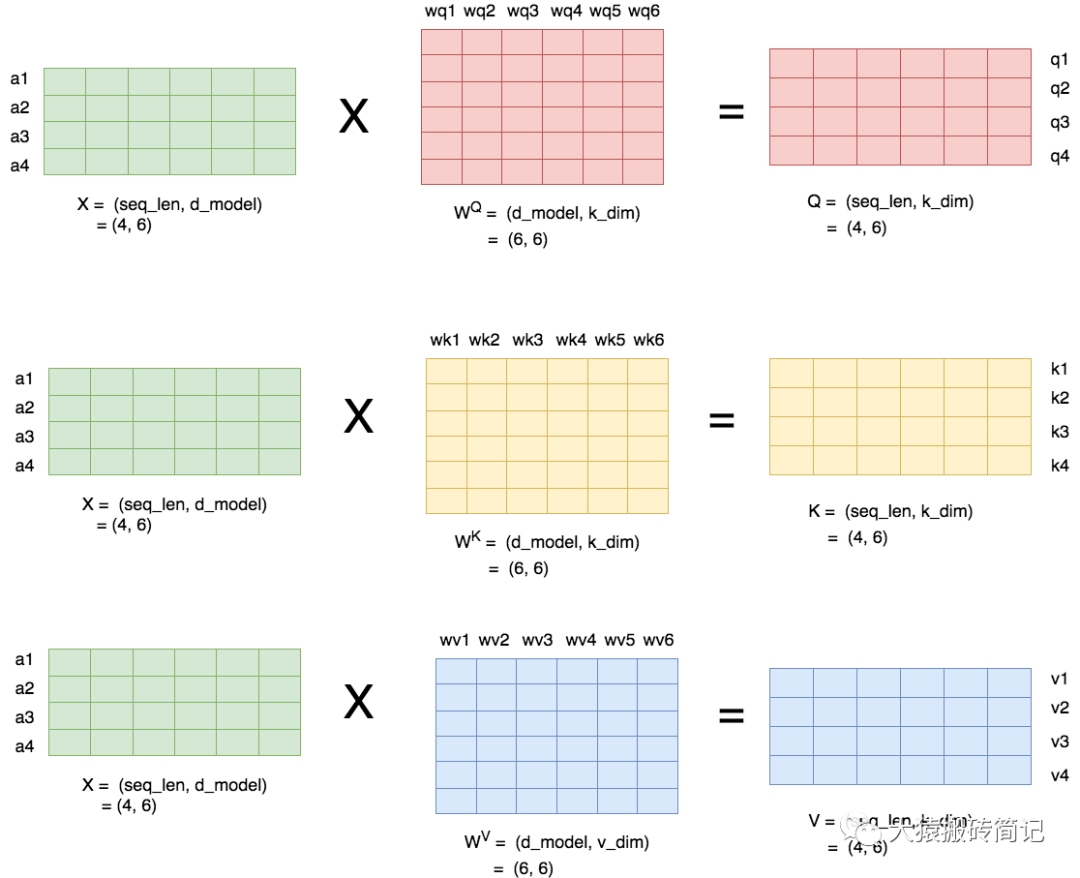
seq_len,d_model分別為本文維度說明中的s和h,也即序列長度和每個token的向量維度
即attention層需要做訓練的三塊權重。
k_dim,v_dim滿足:
理清了單頭,我們來看多頭的情況,下圖展示了當num_heads = 2時attention層的計算方法。即對每一塊權重,我們都沿著列方向(k_dim)維度切割一刀。此時每個head上的的維度都變成(d_model, k_dim//2)。每個head上單獨做矩陣計算,最后將計算結果concat起來即可。整個流程如下:
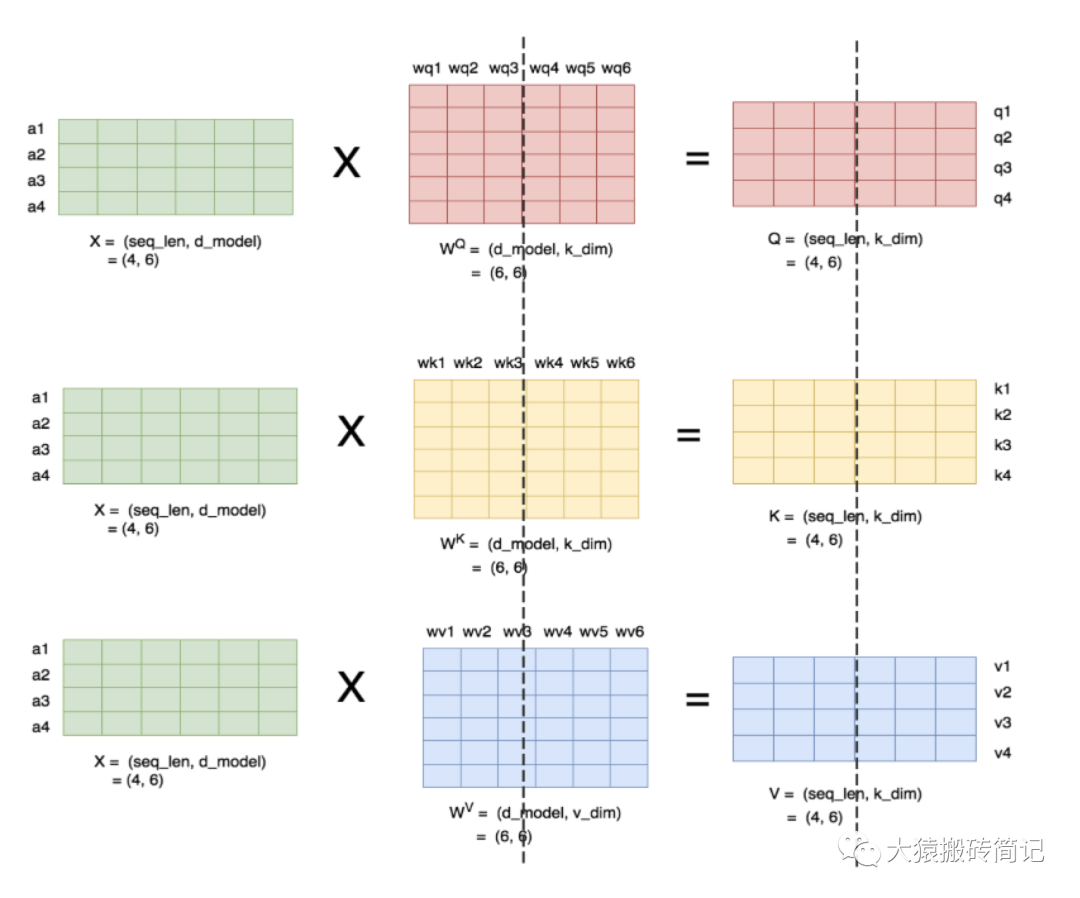
可以發現,attention的多頭計算簡直是為張量模型并行量身定做的,因為每個頭上都可以獨立計算,最后再將結果concat起來。也就是說,可以把每個頭的參數放到一塊GPU上。則整個過程可以畫成:
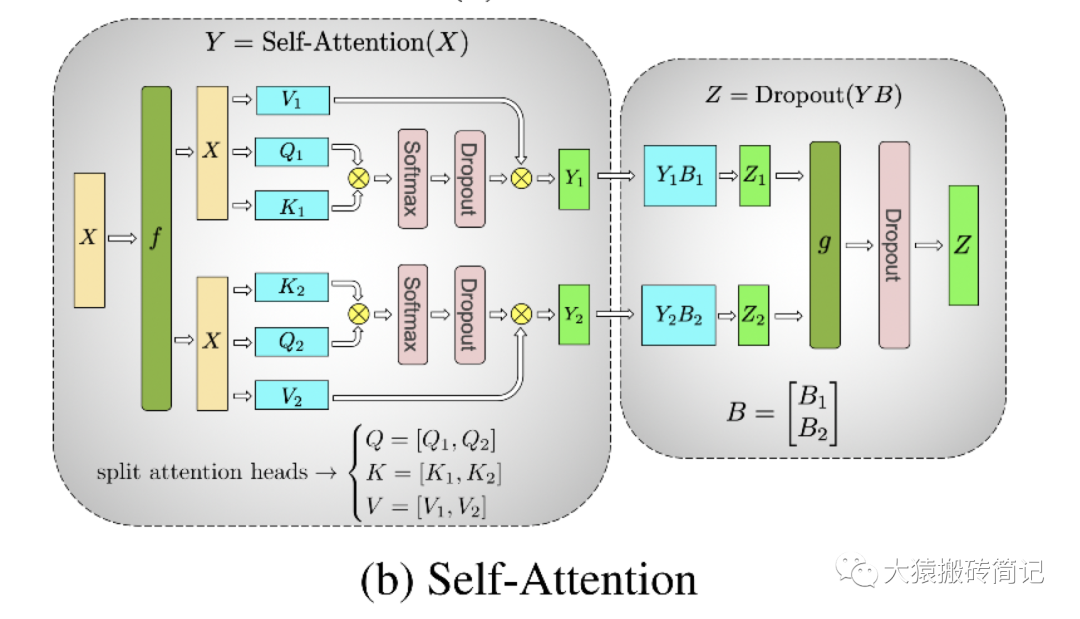
對三個參數矩陣Q,K,V,按照“列切割”,每個頭放到一塊GPU上,做并行計算。對線性層B,按照“行切割”。切割的方式和MLP層基本一致,其forward與backward原理也一致,這里不再贅述。
最后,在實際應用中,并不一定按照一個head占用一塊GPU來切割權重,我們也可以一個多個head占用一塊GPU,這依然不會改變單塊GPU上獨立計算的目的。所以實際設計時,我們盡量保證head總數能被GPU個數整除。
3.2 Self-Attention層的通訊量分析
類比于MLP層,self-attention層在forward中做一次AllReduce,在backward中做一次AllReduce。總通訊量也是,其中
寫到這里,我們可以把self-attention層拼接起來看整體的計算邏輯和通訊量:
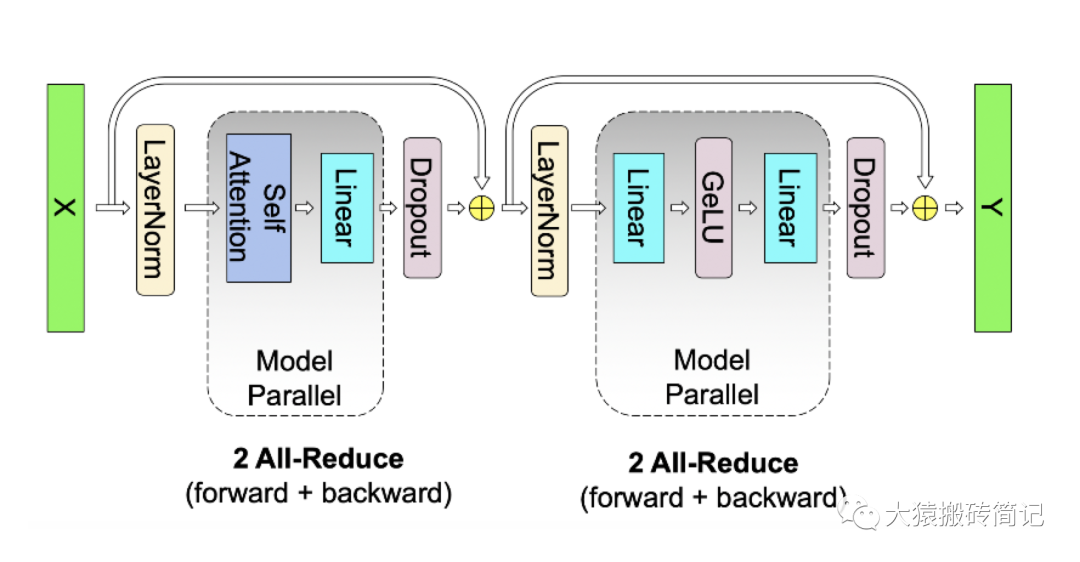
四、Embedding層
講完了中間的計算層,現在我們來看輸入和輸出層。首先看來自輸入層的Embeddng。
4.1 輸入層Embedding
我們知道Embedding層一般由兩個部分組成:
word embedding:維度(v, h),其中v表示詞表大小。
positional embedding:維度(max_s, h),其中max_s表示模型允許的最大序列長度。
對positional embedding來說,max_s本身不會太長,因此每個GPU上都拷貝一份,對顯存的壓力也不會太大。但是對word embedding來說,詞表的大小就很客觀了,因此需要把word embedding拆分到各個GPU上,具體的做法如下:
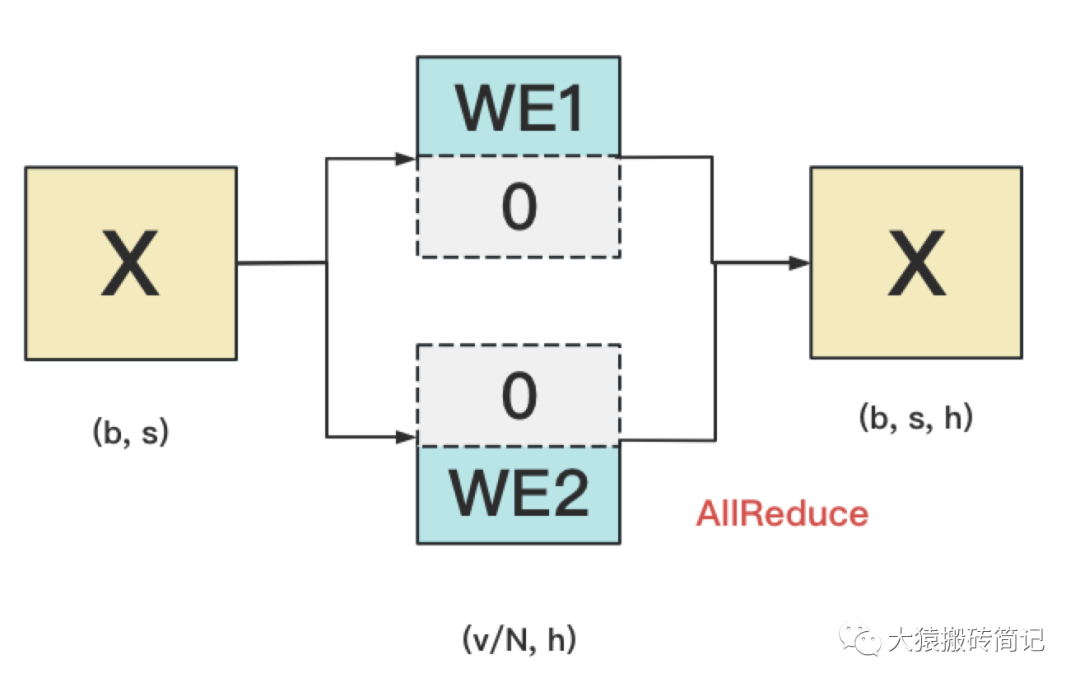
我們來詳細說明下這張圖。對于輸入X,過word embedding的過程,就是等于用token的序號去word embedding中查找對應詞向量的過程。例如,輸入數據為[0, 212, 7, 9],數據中的每一個元素代表詞序號,我們要做的就是去word embedding中的0,212,7,9行去把相應的詞向量找出來。
假設詞表中有300個詞,現在我們將word embedding拆分到兩塊GPU上,第一塊GPU維護詞表[0, 150),第二塊GPU維護詞表[150, 299)。當輸入X去GPU上查找時,能找到的詞,就正常返回詞向量,找到不到就把詞向量中的全部全素都置0。按此方式查找完畢后,每塊GPU上的數據做一次AllReduce,就能得到最終的輸入。
例如例子中,第一塊GPU的查找結果為[ok, 0, ok, ok],第二塊為[0, ok, 0, 0],兩個向量一相加,變為[ok, ok, ok, ok]
4.2 輸出層Embedding
輸出層中,同樣有一個word embedding,把輸入再映射回詞表里,得到每一個位置的詞。一般來說,輸入層和輸出層共用一個word embeding。其計算過程如下:
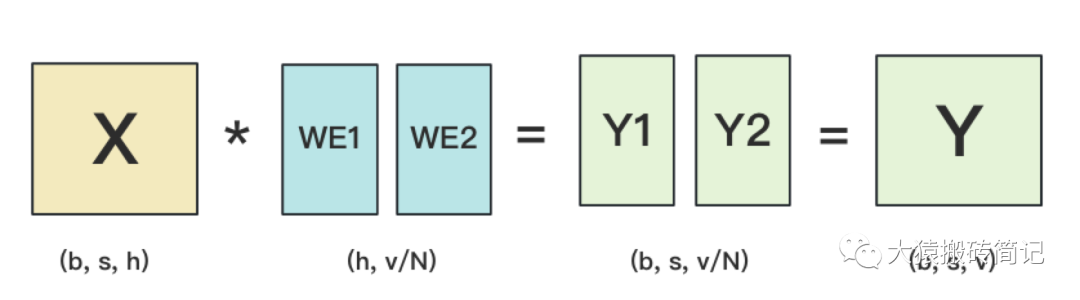
需要注意的是,我們必須時刻保證輸入層和輸出層共用一套word embedding。而在backward的過程中,我們在輸出層時會對word embedding計算一次梯度,在輸入層中還會對word embedding計算一次梯度。在用梯度做word embedding權重更新時,我們必須保證用兩次梯度的總和進行更新。
當模型的輸入層到輸入層都在一塊GPU上時(即流水線并行深度=1),我們不必擔心這點(實踐中大部分用Megatron做并行的項目也是這么做的)。但若模型輸入層和輸出層在不同的GPU上時,我們就要保證在權重更新前,兩塊GPU上的word embedding梯度做了一次AllReduce。現在看得有些迷糊沒關系~在本系列下一篇的源碼解讀里,我們會來分析這一步。
五、Cross-entropy層
終于,我們來到了計算損失函數的一層。回顧一下4.2中,輸出層過完embedding后的樣子:
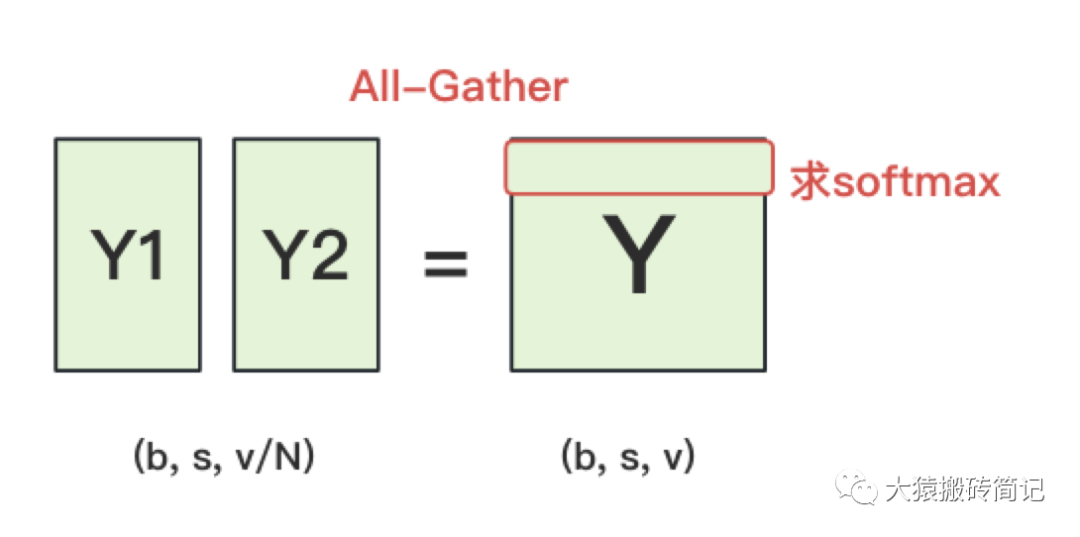
正常來說,我們需要對Y1和Y2做一次All-Gather,把它們concat起來形成Y,然后對Y的每一行做softmax,就可得到對于當前位置來說,每個詞出現的概率。接著,再用此概率和真值組做cross-entropy即可。
但是All-Gather會產生額外的通訊量。當詞表v很大時,這個通訊開銷也不容忽視。針對這種情況,可以做如下優化:
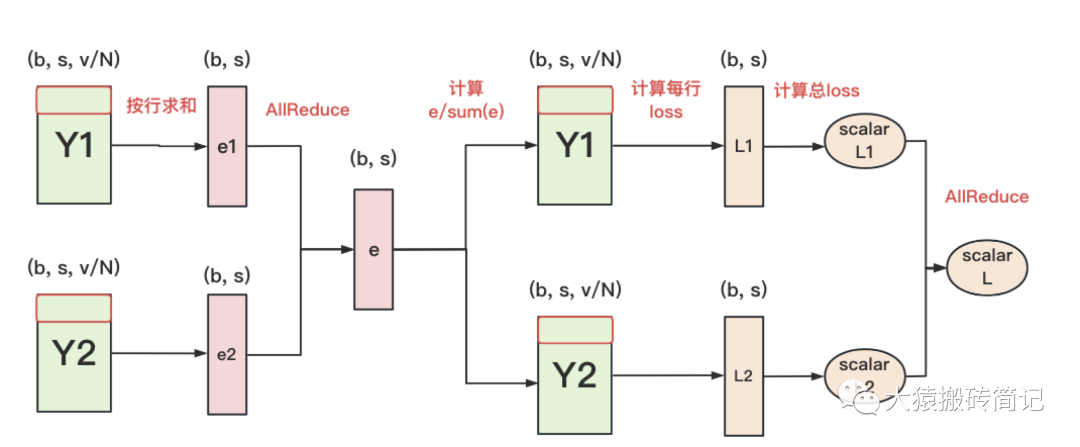
每塊GPU上,我們可以先按行求和,得到各自GPU上的GPU_sum(e)
將每塊GPU上結果做AllReduce,得到每行最終的sum(e),也就softmax中的分母。此時的通訊量為。
在每塊GPU上,即可計算各自維護部分的e/sum(e),將其與真值做cross-entropy,得到每行的loss,按行加總起來以后得到GPU上scalar Loss。
將GPU上的scalar Loss做AllReduce,得到總Loss。此時通訊量為N。
這樣,我們把原先的通訊量從大大降至。
六、張量模型并行 + 數據并行
到這里為止,我們基本把張量模型并行的計算架構說完了。在實際應用中,對Transformer類的模型,采用最經典方法是張量模型并行 + 數據并行,并在數據并行中引入ZeRO做顯存優化。具體的架構如下:
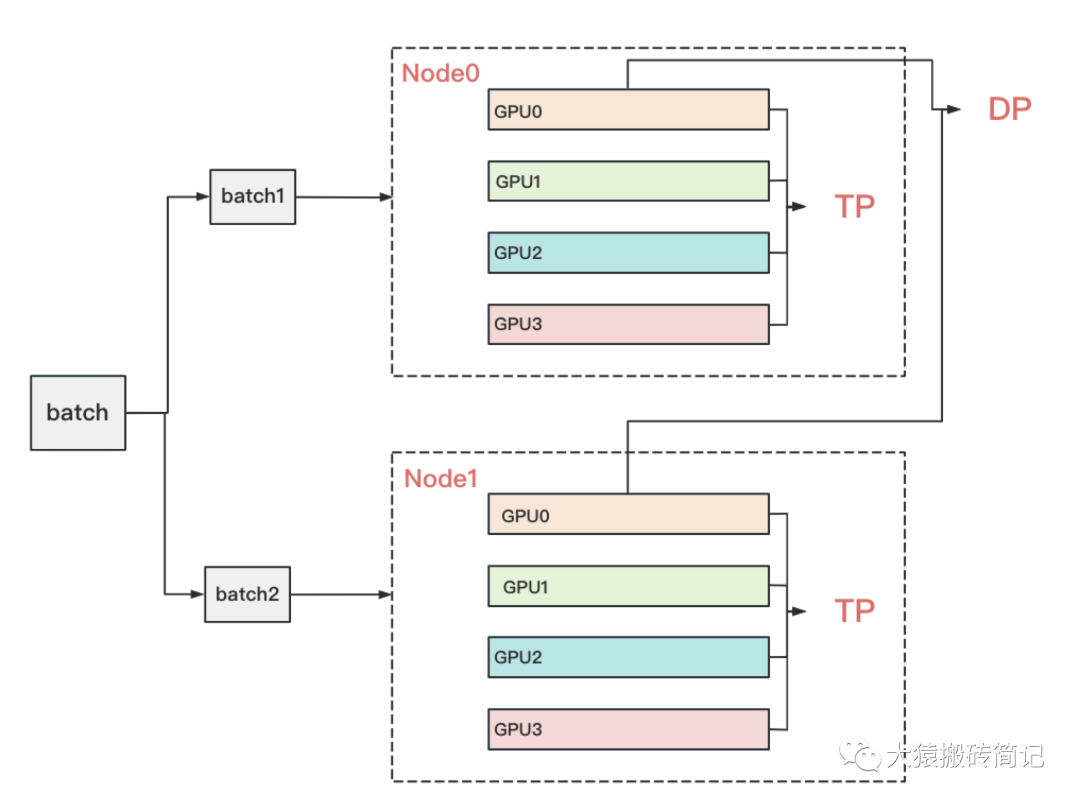
其中,node表示一臺機器,一般我們在同一臺機器的GPU間做張量模型并行。在不同的機器上做數據并行。圖中顏色相同的部分,為一個數據并行組。憑直覺,我們可以知道這么設計大概率和兩種并行方式的通訊量有關。
具體來說,它與TP和DP模式下每一層的通訊量有關,也與TP和DP的backward計算方式有關。我們分別來看這兩點。
6.1 TP與DP通訊量
首先,我們來分析兩者的通訊量。我們關注Transformer中每一層的通訊情況。
在張量模型并行中,我們設每次通訊量為,從上面分析中我們知道每層做2次AllReduce,其通訊總量為。其中,,則通訊總量為。
在數據并行中,設每次通訊量為,從先前的文章中,我們知道每層做1次AllReduce(先不考慮ZeRO拆分權重的情況),其通訊總量為。其中,通訊的主要是梯度,則,總通訊量為。
因此,我們要比較的就是和。忽略常數和共同項,我們最終比較的是:
在實際應用中,前者可能會比后者大一些,但量級基本在左右。因此,從通訊量上來說,有差異但不會顯著(主要還是和模型設計相關)。不過按照常理,通訊量大的,盡量放在一臺機器里(機器內的帶寬大,通訊時間也會小)。通訊量相對小的,可以考慮在不同機器間做并行。
6.2 TP與DP計算backward的方式
回顧上文,我們知道TP在從上一層往下一層做backward的過程中,所有GPU間需要做一次AllReduce的。例如下圖:
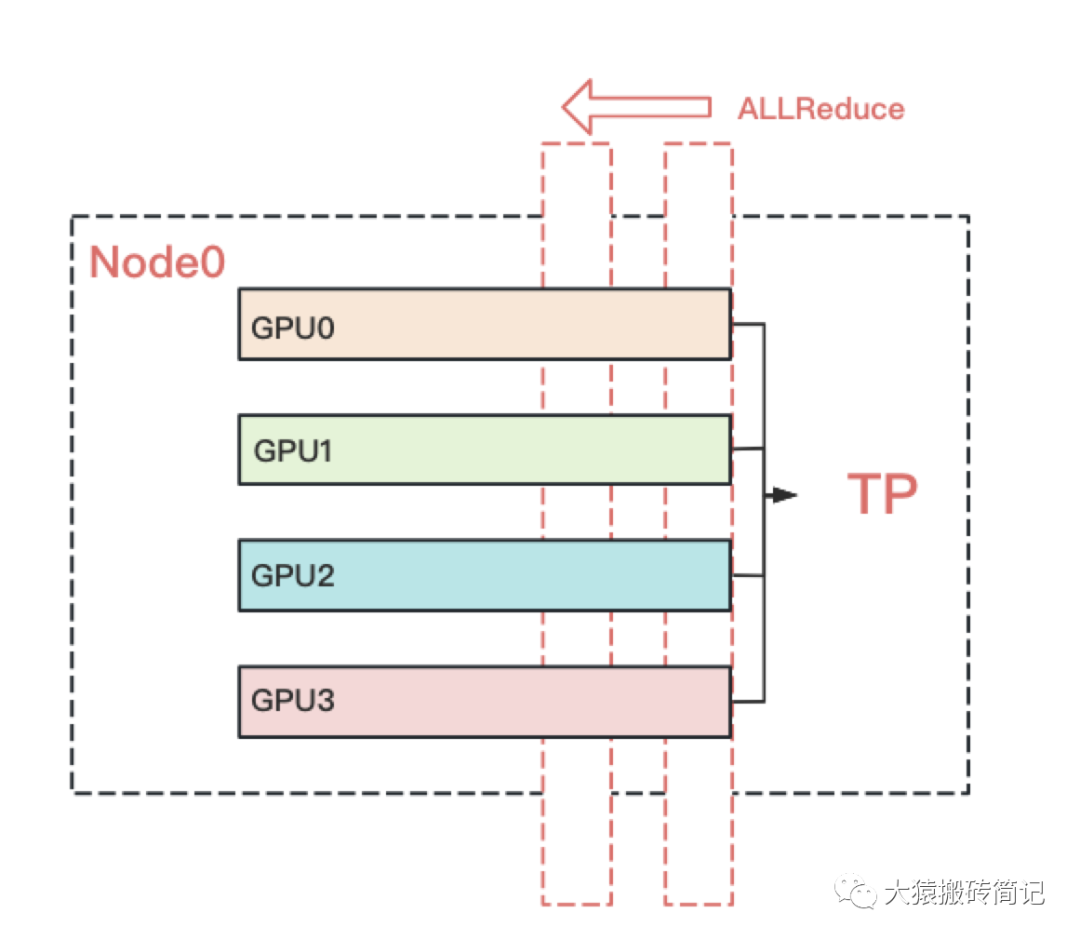
而對DP來說,本層算完梯度以后,就正常把本層的梯度發出去,和屬于一個DP組的GPU做AllReduce,同時繼續往下一層做backward。下一層也是同理。也就是在DP組中,下一層不依賴上一層的梯度聚合結果。因此在DP組中對帶寬的要求就沒那么高了。所以可以放到機器間做DP。例如下圖:
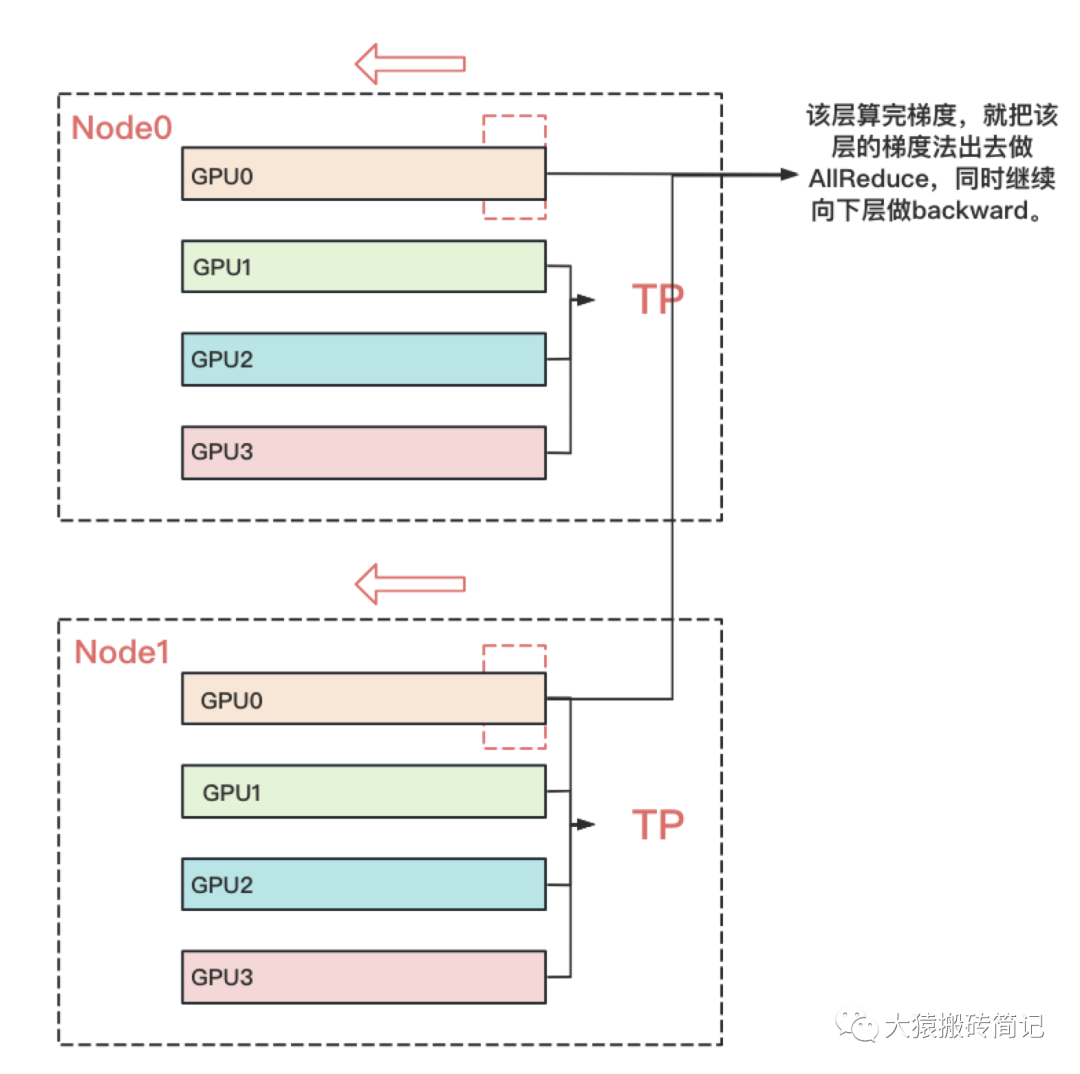
七、實驗效果
在講完Megatron整體的設計后,現在我們可以更好來解讀實驗效果了。在原始論文中,采用32臺DGX-2H,每臺里有16張 Telsa V100 SXM3 32GB的GPU,總共512塊GPU。在這個硬件配置上,訓練不同大小的GPT2模型。核心實驗數據如下:
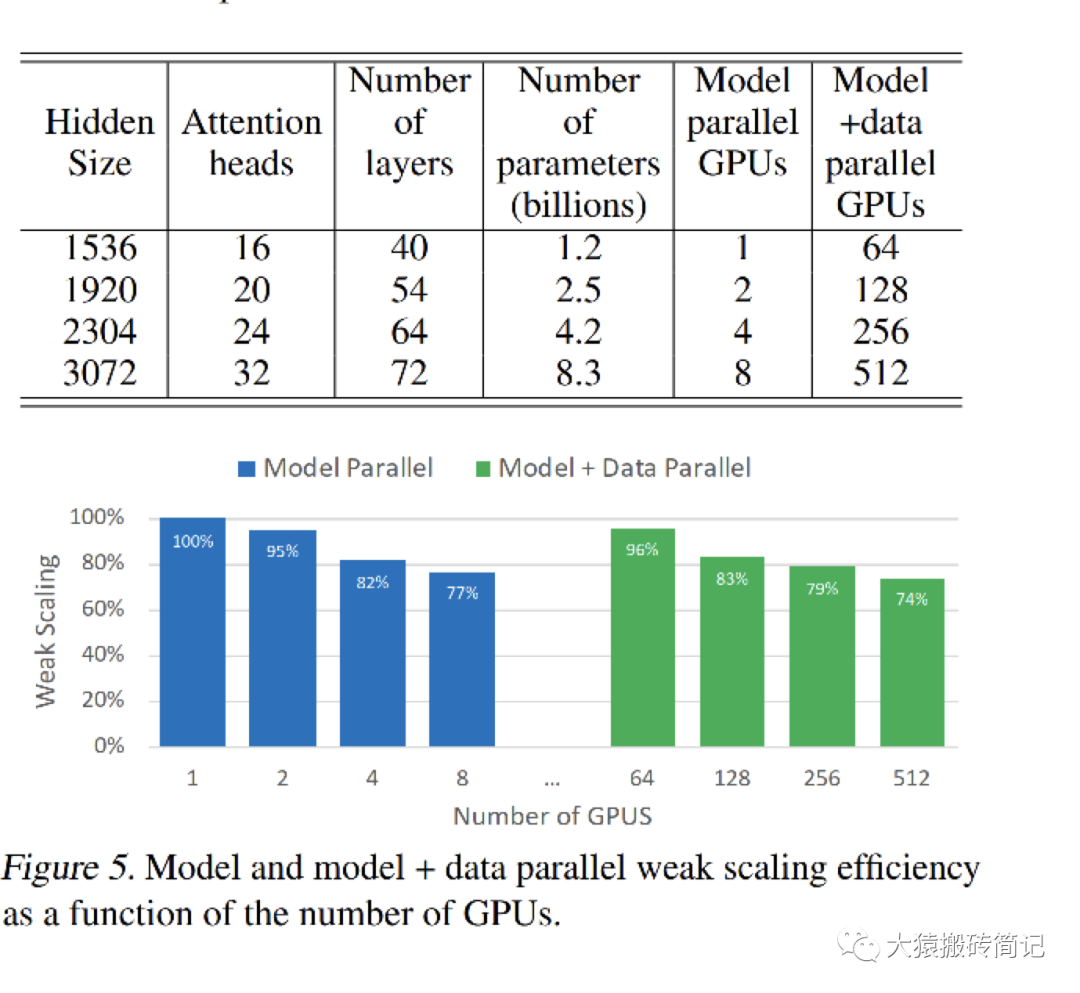
每一行表示模型的不同大小,Model parallel列表示只用TP并行時消耗的GPU卡數,其對應的單卡效率為藍色柱狀圖部分。model + data parallel列表示TP + DP并行時消耗的GPU卡數,單卡計算效率為綠色柱狀圖部分。
7.1 純TP實驗效果
我們先來看純TP部分。表格中的第一行是整個實驗的基線,它設計了一個可以裝在單卡里的GPT模型。此時不涉及卡間的通信,因此GPU的計算效率為100%。
然后,調大GPT模型到需要用2卡做TP。此時因為涉及卡間的通信,所以GPU的計算效率略有下降。從藍色柱狀圖可以看出,隨著模型的增大,需要的GPU數量變多,通訊量增大,單卡的計算效率是在下降的。
從1卡增加到8卡,我們可以發現需要的GPU數量和模型大小是成正比的。例如當參數量從1.2B增加到8.3B,時,需要的GPU數量也對應增加8倍。
但是,到了8以后呢?在這篇論文里,最大只做到了8卡。可是一臺機器明明有16張卡,為啥不能再做到一個16B左右的模型呢?回想上一篇ZeRO部分對顯存消耗的分析,當模型增大時,不僅是參數變多,還有例如activation這樣的中間結果,也在占據大頭顯存。因此需要的GPU數量漸漸不再和模型大小成正比了。如果不引入顯存優化,一臺機器裝不下16B的模型。
7.2 TP + DP實驗效果
再來看TP + DP的結果。表格的第一行是TP + DP的基線。前面說過第一行的模型大小是可以塞進單卡里的。因此,這行中,是在每臺機器中選2塊GPU,一共選擇64塊GPU,每個GPU上都放置了一個完整的模型,GPU間做純數據并行。其單卡計算效率為綠色柱狀圖第1條,96%。
在第二行中,模型大小上升,單卡已裝不下完整模型。因此在每臺機器中,選擇4塊GPU,每2塊GPU組成一個TP組,因此一臺機器上共2個TP組。所有機器上共64個TP組,占據128卡。這些TP組間做數據并行。以此類推模型大小再往上走時的實驗配置。
不難發現,藍色柱狀圖和綠色柱狀圖是一一對應的關系。分別表示單個模型在1卡、2卡、4卡、8卡上時的單卡效率。在引入數據并行的前提下(跨機),綠色的單卡效率并沒有下降很多。這個原因我們在6.2中解釋過:因為DP組內做backward計算梯度時,下一層的計算不需要依賴上一層的梯度AllReduce結果。你算你的,我發我的,對計算通訊比不會產生太大影響。
最后呢,一臺DGX-2H的售價大概是40w刀,這里的硬件成本就有40 * 32 = 1280w刀。要么怎么說Megatron,注定生于NVIDIA家呢?
7.3 GPU效率計算
最后,在實驗這塊,咱們再來說說柱狀圖的weak scaling指標是怎么算出來的。畢竟在論文一開頭,也擺出了一堆指標,乍一看還確實比較迷糊。
首先,在單卡裝下一個模型的情況下,單GPU每秒計算量是39TeraFlOPs(可以近似理解成做矩陣乘法及加法的次數),不涉及通訊,是基線,因此計算效率為100%。
上到512卡的TP + DP后,512卡上總計每秒計算量為15100TeraFlops,因為涉及到通訊,GPU肯定不是每時每刻都在計算的,那么我們到底利用了多少GPU的算力呢?
假設512卡間無任何通訊影響,則理論算力應該為:39 * 512 = 19968TeraFlops,實際算力為15100TeraFlops。則算力利用比 = 15100/19968 = 76%。這就是文章中貫穿的76%這一指標的由來,它體現了即使做分布式訓練,GPU的計算能力也不會被通信浪費掉太多,這也是Megatron的賣點之一。
關于Megatron的理論介紹,就寫到這里啦!在大模型訓練的下個篇章里,我們將一起讀Megatron的源碼,一起學習經典的大模型預訓練方法,順便看看Megatron的第二個賣點:“我們的代碼用起來很簡單!”是不是個事實(狗頭
-
數據
+關注
關注
8文章
7134瀏覽量
89398 -
API
+關注
關注
2文章
1510瀏覽量
62293 -
模型
+關注
關注
1文章
3298瀏覽量
49074 -
Transformer
+關注
關注
0文章
145瀏覽量
6032 -
大模型
+關注
關注
2文章
2541瀏覽量
3024
原文標題:圖解大模型系列之:張量模型并行,Megatron-LM
文章出處:【微信號:GiantPandaCV,微信公眾號:GiantPandaCV】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
【大語言模型:原理與工程實踐】大語言模型的基礎技術
【大語言模型:原理與工程實踐】大語言模型的預訓練
超大Transformer語言模型的分布式訓練框架
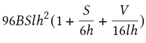
探究超大Transformer語言模型的分布式訓練框架
一種基于亂序語言模型的預訓練模型-PERT
利用視覺語言模型對檢測器進行預訓練
PyTorch教程11.9之使用Transformer進行大規模預訓練

PyTorch教程-11.9. 使用 Transformer 進行大規模預訓練
基于PyTorch的模型并行分布式訓練Megatron解析




 基于Transformer做大模型預訓練基本的并行范式
基于Transformer做大模型預訓練基本的并行范式










評論